控制点因素对GPS坐标系统转换精度的影响

GPS测量中的坐标系转换第一章绪论1.1概述坐标转化并不是一个新的课题,随着测绘事业的发展,全球一体化的形成,越来越要求全球测绘资料的统一。

尤其是在坐标系统的统一方面.原始的大地测量工作主要是依靠光学仪器进行,这样不免受到近地面大气的影响,同时受地球曲率的影响很大,在通视条件上受到很大的限制,从而对全球测绘资料的一体化产生巨大的约束性。

另外由于每一个国家的大地坐标系的建立和发展具有一定的历史特性,仅常用的大地坐标系就有150余个。

在同一个国家,在不同的历史时期由于习惯的改变或经济的发展变化也会采用不同的坐标系统。

例如:在我国建国之后,为了尽快搞好基础建设,我国采用了应用克氏椭球与我国实际相结合的北京54坐标系;随着经济的发展北京54坐标系的缺陷也随之被表露的越来越明显,特别是对我国经济较发达的东南沿海地区的影响表现得更为明显,进而我国开始研究并使用国家80坐标系。

在实际生活中,在一些地区由于国家建设的急需,来不及布设国家统一的大地控制网,而建立局部的独立坐标系。

而后,再将其转换到国家统一的大地控制网中,这些坐标系的变换都离不开坐标值的转化.在国际上,随着1964年美国海军武器实验室对第一代卫星导航系统─NNSS的研制成功,为测绘资料的全球一体化提供了可能。

到1972年,经过美国国防部的批准,开始了第二代卫星导航系统的开发研究工作,即为现在所说的GPS。

此套卫星导航系统满足了全球范围、全天候、连续实时以及三维导航和定位的要求.正是由于GPS卫星的这些特性,这种技术就很快被广大测绘工作者接受。

是由于坐标系统的不同,对GPS技术的推广使用造成了一定的障碍。

这样坐标转换的问题再一次被提到了重要的位置。

为了描述卫星运动,处理观测数据和表示测站位置,需要建立与之相应的坐标系统。

在GPS测量中,通常采用两种坐标系统,即协议天球坐标系和协议地球坐标系。

其中协议地球坐标系采用的是1984年世界大地坐标系(Word Geodetic System 1984─WGS-84)其主要参数为:长半轴 a=6378137; 扁率 f=1:298.257223563.而我国采用的坐标系并不是WGS-84坐标系而是BJ-54坐标系,这个坐标系是与前苏联的1942年普耳科沃坐标系有关的,其主要参数为: 长半轴 a=6378245; 扁率 f=1:298.3.这就使得同一点在不同的坐标系下有不同的坐标值,这样使测绘资料的使用范围受到很大的限制,并且对GPS系统在我国的广泛使用造成了一定的约束性,对我国的测绘事业的发展不利。

点校正就是求出WGS-84和当地平面直角坐标系统之间的数学转换关系（转换参数）。

在工程应用中使用GPS卫星定位系统采集到的数据是WGS-84坐标系数据，而目前我们测量成果普遍使用的是以1954年北京坐标系或是地方（任意|当地）独立坐标系为基础的坐标数据。

因此必须将WGS-84坐标转换到BJ-54坐标系或地方（任意）独立坐标系。

坐标系统之间的转换可以利用现有的七参数或三参数，也可以利用华测测地通软件进行点校正求四参数和高程拟合。

单点校正：利用一个点的WGS84坐标和当地坐标可以求出3个平移参数，旋转为零，比例因子为1。

在不知道当地坐标系统的旋转、比例因子的情况下，单点校正的精度无法保障，控制范围更无法确定。

因此建议尽量不要使用这种方式。

两点校正：可求出3个坐标平移参数、旋转和比例因子，各残差都为零。

比例因子至少在0.9999***至1.0000****之间，超过此数值，精度容易出问题或者已知点有问题；旋转的角度一般都比较小，都在度以下，如果旋转上百度，就要注意是不是已知点有问题三点校正：三个点做点校正，有水平残参，无垂直残差。

四点校正：四个点做点校正，既有水平残参，也有垂直残差。

点校正时的注意事项：1、已知点最好要分布在整个作业区域的边缘，能控制整个区域，并避免短边控制长边。

例如，如果用四个点做点校正的话，那么测量作业的区域最好在这四个点连成的四边形内部；2、一定要避免已知点的线形分布。

例如，如果用三个已知点进行点校正，这三个点组成的三角形要尽量接近正三角形，如果是四个点，就要尽量接近正方形，一定要避免所有的已知点的分布接近一条直线，这样会严重的影响测量的精度，特别是高程精度；3、如果在测量任务里只需要水平的坐标，不需要高程，建议用户至少要用两个点进行校正，但如果要检核已知点的水平残差，那么至少要用三个点；如果既需要水平坐标又需要高程，建议用户至少用三个点进行点校正，但如果要检核已知点的水平残差和垂直残差，那么至少需要四个点进行校正；4、注意坐标系统，中央子午线，投影面（特别是海拔比较高的地方），控制点与放样点是否是一个投影带；5、已知点之间的匹配程度也很重要，比如GPS观测的已知点和国家的三角已知点，如果同时使用的话，检核的时候水平残差有可能会很大的；6、如果有3个以上的点作点校正，检查一下水平残差和垂直残差的数值，看其是否满足用户的测量精度要求，如果残差太大，残差不要超过2厘米，如果太大先检查已知点输入是否有误，如果无误的话，就是已知点的匹配有问题，要更换已知点了；7、对于高程要特别注意控制点的线性分布（几个控制点分布在一条线上），特别是做线路工程，参与校正的高程点建议不要超过2个点（即在校正时，校正方法里不要超过两个点选垂直平差的）。

《GPS定位原理与应用》习题集答案第一篇《GPS定位原理与应用》习题集一、名词解释一、名词解释I、卫星星历:是描述卫星运行轨道的信息。

2、天线高:指天线的相位中心至观测点标志中心顶面的垂直距离。

3,春分点:当太阳在黄道上从天球南半球向北半球运行时，黄道与地球赤道的交点。

4、开普勒第一定律:卫星运行的轨道是一个椭圆，而该椭圆的一个焦点与地球的月心相重合。

这一定律表明，在中心引力场中，卫星绕地球运行的轨道面，是一个通过划球质心的静止平面。

5、同步环:由多台接收机同步观测的结果所构成的闭合环称为同步环。

6、多路朽效应:在GPS测量中，如果测站周围的反射物所反射的卫星信号(反射波)进入接收衫天线，这就将和直接来自卫星的信号(直接波)产生干涉，从而使观测值偏离真值产且所谓的多路径误差。

这种山于多路径的信号传播所引起的干涉时延效应称为多路径效应。

、7、周跳:在接收机跟踪GPS卫星进行观测的过程中，常常山于多种原因(例如接收机天线被阻挡、外界噪声信号的千扰等)，可能使载波相位观测值中的9周数不正确但其不足1整周的小数部分仍然是正确的，这种现象成为整周变跳，简称周跳。

8、绝对定位:利用GPS卫星和用户接收机间的距离观测值直接确定用户接收机天线在在WGS-84坐标系中相对地球质心的绝对位置。

9,恒星时:以春分点为参考点，由春分点的周日视运动所确定的时间，称为恒星时。

恒星时是地方时。

10、卫星的无摄运动:卫星在轨运动受到中心力和摄动力的影响。

假设地球为匀质|球体，其对卫星的引力称为中心力(质量集中于球体的中心)。

中心力决定着卫星运动的4本规律和特征，此时卫星的运动称为无摄运动，山此所决定的卫星轨道可视为理想的轨道，又称卫星的无摄运动轨道。

11,精密星历:是一些国家的某些部门，根据各自建立的跟踪站所获得的精密观测资料，应用与确定预报星历相似的方法，而计算的卫星星历。

它可以向用户提供在用户观测时间的卫星星历，避免了预报星历外推的误差。

《GPS测量原理与应用》练习题二一、名词解释1、同步环由多台接收机同步观测所构成的闭合环称为同步环。

2、重复观测边同一基线边，若观测了多个时段（>=2）, 则可得到多个基线边长。

这种具有多个独立观测结果的基线边，称为重复边。

3、异步环在构成多边形环路的所有基线向量中，只要有非同步观测向量的，则该多边形环路叫做异步观测环，简称异步环。

4、相对论效应是由于卫星钟和接收机钟所处的状态（运动速度和重力位）不同而引起卫星钟和接收机钟之间产生相对钟误差的现象。

5、大气折射对于GPS而言，卫星的电磁波信号从信号发射天线传播到地面GPS接收机天线，其传播路径并非真空，而是要穿过性质与状态各异、且不稳定的大气层，使其传播的方向、速度和强度发生变化，这种现象称为大气折射。

6、观测时段测站上开始接收卫星信号到观测停止，连续工作的时间段，称为观测时段，简称时段。

7、独立观测环由独立观测所获得的基线向量构成的闭合环，简称独立环。

8 GPS相对定位的作业模式利用GPS确定观测站之间相对位置所采用的作业方式。

它与GPS接收机设备的软件和硬件密切相关。

同时，不同的作业模式因作业方法、观测时间和应用范围的不同而有所差异。

9、坐标联测点GPS网平面坐标系统转换，通常是采用坐标联测来实现的。

采用GPS定位技术，重测部分地面网中的高等级国家控制点。

这种既具有WGS-84坐标系下的坐标，又具有参考坐标系下的坐标的公共点，称为GPS网和地面网的坐标连测点（简称坐标联测点）。

坐标联测点是显示坐标转换的前提。

10、高程联测点利用GPS直接测定的高程是GPS点在WGS-84坐标系中的大地高，而实际工作中通常需要的是正常高，为实现高程系统的转换，在布设GPS网时，需采用几何水准方法联测部分GPS点，这些被联测的GPS点，称为水准联测点。

11、停测段在某一测站上，若在某一时间段内可测卫星只有4颗，而这4 颗卫星的图形分布很差，其几何精度因于GDOpg过了规定的要求，以致无法保证预订的定位精度。

2021年注册测绘师考试真题：案例分析(文字版)2021年度全国注册测绘师资格考试试卷测绘案例分析第一题(18分)某市的基础控制网，因受城市建设，自然环境、认为活动等因素的影响，测量标志持续破坏，减少。

为了博阿正基础控制网的功能，该市决定对基础控制网实行维护，主要工作内容包括控制点的普查、补测、观测、计算及成果的坐标转换等。

1 已有资料情况该市基础控制网的观测数据及成果：联测国家高等级三角点5个，基本均匀覆盖整个城市区域，各三角点均有1980西安坐标系成果;城市及周边地区的GPS连续运行参考站观测数据及精确坐标;城市及周边地区近期布设的国家GPS点及成果。

2 控制网测量精度指标要求控制网采用三等GPS网，主要技术指标见下表：等级最弱边相对中误差三等≤10≤51/80 0003 外业资料的检验使用随接收机配备的商用软件对观测数据实行解算，对同步环闭合数、独立闭合环闭合差、重复基线较差实行检核，各项指标应满足精度要求：A. 同步环各坐标分量闭合差B. 独立闭合坐标闭合差和各坐标分量闭合差C. 重复基线的长度较差应满足规范要求项目实施中，测得某一基线长度约10 公里，重复基线的长度较差95.5毫米，某一由6条边(平均边长约5公里)组成的独立闭合环，其X、Y、Z坐标分量的闭合差分别为60.4毫米、160.3毫米、90.5毫米。

4 GPS控制网平差解算A. 三维无约束平差B. 三维约束平差5 坐标转换该市基于2000国家大地坐标系建立了城市独立坐标系，该独立坐标系使用中央子午线为东经×××°××′××"，任意带高斯平面直角坐标。

通过平差与严密换算获得城市基础控制网2000国家大地坐标系与独立坐标系成果后，利用联测的5个高等级三角点成果，采用平面二维四参数转换模型，获得了该基础控制网1954年北京坐标系与1980西安坐标系成果。

坐标转换中用于计算七参数的公共点数量对转换结果精度影响的研究本文结合国土空间数据转换项目;在某县2700多平方公里区域内，首先分别选择5个、15个、30个和60个公共点计算用于数据转换的七参数;利用分别计算的布尔莎七参数对同一待转数据进行转换，对转换结果进行了精度对比分析，得出一些在县级区域坐标转换方面有益的结论。

标签：坐标转换;公共点;精度分析1980西安坐标系数据转换为国家2000大地坐标系，实际是将参心坐标系转换为地心坐标系;根据待转区域面积大小以及待转换数据的类型、格式、比例尺等不同，其转换方法也有多种;本项目使用的布尔莎七参数模型，需要提供三个平移、三个旋转和一个尺度参数共计七个转换参数;而计算这七个参数需要在转换区域均匀选择一些同时拥有80和2000坐标系坐标的公共点进行计算。

原理上只要有3个公共点即可以计算出七参数;然而公共点应该选择几个最合适，是不是越多最好？本文从实际转换项目出发，对这一问题进行研究论证。

1、转换参数计算步骤（1）选择布尔莎转换模型;（2）选用有西安80坐标系坐标和2000国家大地坐标系坐标的控制点作为公共点。

（3）将两种坐标系下的坐标都转换为空间直角坐标系下的坐标;（4）将公共点坐标代入转换模型，利用最小二乘法计算转换参数;（5）用得到的转换参数计算检核点坐标残差;（6）剔除残差大于3倍点位中误差的公共点，再在附近补充选择其他公共点;（7）重复上述3）到6）的计算过程，直至所有公共点坐标残差均小于3倍点位中误差;（8）根据最终确定的公共点，利用最小二乘法计算转换参数。

2、不同数量公共点对转换结果的影响2.1公共点选择以本项目为例，为进行全县的坐标转换，在覆盖全县区域共布设154个GPS 控制点，具体标准严格按照《全球定位系统（GPS）测量规范》（GB/T 19314-2009）中关于D级GPS控制网的要求进行执行。

2.2检核点选择除以上所选的60个公共点外，在整个区域内均匀选择了20个其他不参与参数计算的公共点，作为公共点残差检验点，并用于转换精度分析。

ＧＰＳ（ＲＴＫ）技术在控制测量中的应用作者：林福棋来源：《沿海企业与科技》2008年第02期［摘要］文章通过简述GPS(RTK)基本工作原理，结合某测区控制测量的应用，对GPS(RTK)技术控制测量精度的可靠性作出分析，并提出工作中的注意事项及应对方法。

［关键词］GPS(RTK)技术; 控制测量；应用［作者简介］林福棋，福建省漳州水工环地质勘查测绘院，福建省闽南地质大队，工程师，福建漳州，363000［中图分类号］ P244 ［文献标识码］ A ［文章编号］ 1007-7723（2008）02-0038-0002一、引言随着先进的GPS技术的发展以及GPS接收机空间定位精度的不断提高，GPS(RTK)技术已经被广泛地应用到控制测量、地形地籍测量、房产测量、工程测量等测量领域。

使用RTK技术进行空间定位具有定位精度高、观测时间短、测站之间无需通视、操作简便和全天候作业等优点。

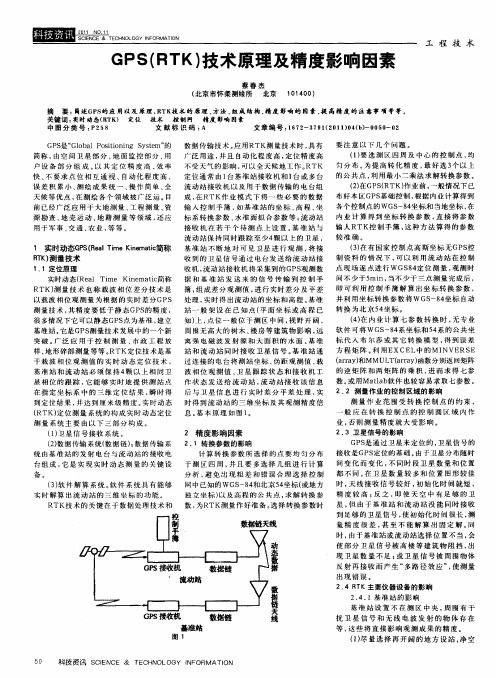
二、 GPS(RTK)技术工作原理GPS(RTK)系统由GPS接收设备、无线电通讯设备、电子手簿及配套设备组成，是以载波相位测量为依据的实时差分GPS测量技术。

它是在基准站安置一台GPS双频接收机，对卫星进行连续观测，并将连续观测到的信息和基准站的信息通过无线电传输设备传送出去。

在流动站上，GPS接收机除接收卫星信号外同时还接收来自基准站发来的数据信息，并通过仪器内置软件实时解算出三维坐标信息及其精度信息。

三、GPS(RTK)在控制测量中的应用（一）测区概况本测区为1∶1000数字化地形测量，位于漳州某开发区内，测绘面积10平方公里。

测区为丘陵地带，地势较为平坦，平均海拔高程32米左右，地势是东北高、西南低。

测区内房屋密集，植被丰富，有大部分的高杆经济作物，通视条件差，按传统的作业方法进行图根导线测量难度很大。

为此，我们采用新技术和新方法，采用南方测绘仪器有限公司生产的灵锐S82型GPS(RTK) 测量仪器对测区进行图根控制测量，该仪器的技术指标为平面精度为±（10mm＋1ppm）,高程精度为±（20mm＋1ppm）。

GPS-RTK技术在工程测量中的应用摘要：随着社会经济建设的不断发展，基础工程建设也在扩大，测量技术的要求也越来越高。

在工程方面，由于工作条件和能见度方面的限制，常规工程技术无法再满足测量精度的要求。

当时，全球定位系统-RTK技术应运而生，仅满足了当时的发展需要，并广泛用于工程测量。

关键词：GPS-RTK技术；工程测量；应用策略引言在工程测量中应用GPS-RTK技术，其具有定位精准度高、自动化水平高等优点，且能突破时间与空间的约束，实现24h全天候定位，其现场观测时，不会耗用较多的时间成本，能给工程测量人员提供可靠的信息支持。

实践中，技术人员可以依照GPS-RTK技术定位要求，立足于工程现场实际，分析并确定工程测绘内容，采用GPS-RTK技术实现整体统筹规划，进而显著提升测量工作质量与效率。

1GPS-RTK技术在工程测量工作中的原理和特点GPS RTK技术用于工程测量，其应用的主要原理是基于载波相位的差分实时GPS技术。

作为实际工程测量工作的一部分，其系统主要包括卫星信号接收系统、数据处理和传输系统。

(1)在对GPS RTK进行专门技术调查期间，工作人员通过参考站传送测量的卫星数据和测站信息，然后移动站根据参考站收到的信息调整该站的数据信息，最后获得关于技术测量定位的最准确信息。

(2)在技术测量中应用GPS RTK技术时，工作人员应在参考站安装一个信息接收器，然后安装一个移动站，该移动站可根据实际技术测量的需要进行配置。

工作过程中，罗夫站和参考站必须同时站起来接收GPS卫星传输的信号，以帮助工程水工获得罗夫站位置的准确坐标。

与我国传统的工程勘测技术相比，GPS RTK技术具有许多优点，具体如下：（1）工程采纳过程更加直观。

通过应用GPSRTK技术，可以显示项目的实时勘测结果，方便测量员随时检查工程坐标;（2）测量时间短。

通过应用GPS RTK技术，可以在5秒内访问高精度的工程三维坐标，并且所需的工程测量时间比传统测量技术更短。