当前位置：文档之家 › 运筹学(第三章)课件

运筹学(第三章)课件

  • 格式：ppt
  • 大小：1.44 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

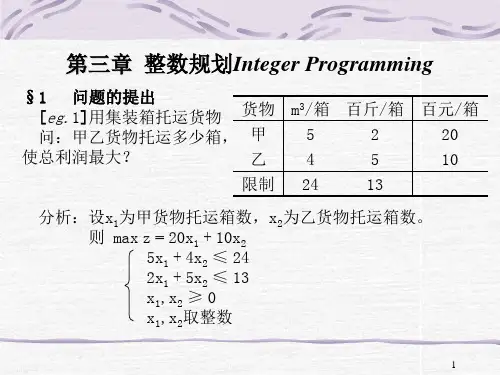
运筹学PPT——第三章

运筹学PPT——第三章

第三章整数规划Integer Programming§1问题的提出[eg.1]用集装箱托运货物问：甲乙货物托运多少箱，使总利润最大？货物m3/箱百斤/箱百元/箱甲5220乙4510限制2413分析：设x1为甲货物托运箱数，x2为乙货物托运箱数。

则max z= 20x1+10x25x1+4x2≤242x1+5x2≤13x 1,x2≥0x 1,x2取整数图解法：x 1x 24321012 4.8①2.6②(4,1)∴x 1*= 4 x 2*= 1 z I *= 90一般，整数规划的最优解不会优于相应线性规划的最优解。

对于max 问题，z I * ≤z l *对于min 问题，z I *≥ z l *数学模型：取整数j j nj iijij nj jj x nj x m i b xa x c z ,,10,,1max 11 =≥=≤=∑∑==§2 分枝定界法用单纯形法，去掉整数约束IP LP xl*判别是否整数解x I *= xl*Yes去掉非整数域No多个LP……§3 0-1规划（xi= 0或1的规划）[eg.2]选择投资场所A i 投资Bi元，总投资≤B，收益Ci元.问：如何选择Ai ，使收益最大？A6A7A4A5A3A2A1最多选2个最少选1个最少选1个分析：引入xi= 1 A i选中0 Ai落选max z= C1x1+C2x2+… +C7x7x 1+x2+x3≤2x 4+x5≥1x 6+x7≥1B 1x1+B2x2+… +B7x7≤Bx i = 0或1南区西区东区[eg.3]求解如下0-1规划max z= 3x1-2x2+5x3x1+2x2-x3≤2 ①x 1+4x2+x3≤4 ②x 1+x2≤3 ③4x2+x3≤6 ④x 1,x2,x3= 0或1解：(1)观察一个可行解x1= 1 x2= x3= 0此时，z= 3(2)增加一个过滤条件3x1-2x2+5x3≥3 *(3)列表计算x x x *可行？z0015√51003110√3123①②③④0000×-1115010-2×01131×110180211√81101×111626×∴ 最优解：x 1*= 1 x 2*= 0 x 3*= 1 此时，z *= 8第四章。

运筹学 PPT3

运筹学 PPT3

2005/05
-10-
---第 3 章 线性规划---
例2：合理下料问题：
要制作1000套钢筋架子，每套含2.9米、2.1米、1.5 米的钢筋各一根。已知原料长7.4米，问：如何下料，使 用料最省？
长度
Ⅰ
1
Ⅱ
2
Ⅲ
Ⅳ
1
Ⅴ
2.9米 2.1米
2
2 7.1 0.3
1
1.5米
合计(米) 料头(米)
2005/05
2. 应用程序 规划求解——Solver for Excel 电子表格（spreadsheet）程序 LINDO——LINDO公司开发，用于个人机，教 学，商用 What’s Best! for LOTUS 1-2-3 类似规划求解（Solver）程序，windows平台
2005/05 -30-
x12 200,000
x21+ x23300,000 x12+ 0.2 x11 x23 150,000 x31+ x34300,000 x23 +0.2(x11+ x21)+0.5x12 x34100,000
2005/05
xij0, (i=1,2,3; j=1,2,3,4)
-14-
---第 3 章 线性规划---
例4：排班问题
一家昼夜服务的大饭店，24小时中需要的服务员数 如下表所示。每个服务员每天连续工作8小时，且在时 段开始时上班。问：最少需要多少名服务员？试建立 该问题的线性规划模型。
起迄时间 2----6 时 6---10 时 10--14 时 14--18 时 18--22 时 22---2 时
2005/05
（2） 要求所解决的问题的目标可用数值指标描述， 并且能表示成线性函数；

运筹学教学课件 第三章 运输问题

运筹学教学课件 第三章 运输问题

7 4 9 3 6 5 6
2.1 确定初始基可行解
• 这与一般线性规划问题不同，产 销平衡的运输问题总是存在可行解。 因有
b a
i 1 j i 1
m
m
i
d
必存在 0≤ xij,i=1,…,m,j=1,…,n 是可行解。又因 0≤xij≤min(a1,bj) • 故运输问题的可行解和最优解必存在。 • 确定初始可行解的方法有很多，一般 希望的方法即简便又尽可能接近最优解。 下面介绍两种方法：最小元素法和伏格 尔（Vogel）法。（其它如西北角法等）
例1
• 某公司经销甲产品，它下设三个加工厂。每 日的产量分别为： • A1——7吨，A2——4吨，A3——9吨。该公 司把这些产品分别运往四个销售点。各销售 点每日的销量为：B1——3吨，B2——6吨， • B3——5吨，B4——6吨。已知从各工厂到各 销售点的单位产品的运价为表3-3所示，问该 公司应如何调运产品，在满足各销点的需要 量的前提下，使总运费为最少。
运价表与行差和 列差的计算
表3-10 伏格尔法
伏格尔法基可行解， 总运费为85，恰好得 到最优解
销地 B1 B2 B3 B4 行 产 差 量 产地
销地 B1 B2 B3 B4 产地 A1 A2
A1
A2 A3
3
1 7
11 3
9 4 5 6 2 1 5
10 0
8 3 6 1 1
7
4 9
10 5
列差 2 销量 3
A3
表3-13
B1 销地 加工厂 A1 A2 A3 销量 ห้องสมุดไป่ตู้2 B3 B4 产量
5 3 6 3 6 5
2 1 3 6
7 4 9

运筹学第三章课件

运筹学第三章课件

B3
3 2 10 ３
B4
10 8 5
日产量
罚金成本
A1 A2 A3
销量 罚金成本
7 4 9-6
0 1 1
０ 1 ２
②
6 5
5 1
6 -３ 3
①
1.5 表上作业法
③重复步骤②，直至求得求得初始调运方案。与最小元素法相同，最后表中 应有m＋n－1个数字格。对应初始基本可行解的m＋n－1个基变量。
x13 =5,x14 =2,x 21 =3,x 24 =1,x 32 =6,x 34 = 3
······
0
i=m j=1 j=2
0 1 0
······
······ 0 ···· ···· ·· 0 ······ 0 0 1 ······
0 1 0
······
······ 1 ···· ···· · 0 ······ 0 0 1
0 ······ 0 ···· ···· ·· 1 ······ 0 ······
日产量（吨）
A1 A2 A3
日销量（吨）
7 4 9
问该公司应如何确定调运方案，在满足各销地需求量的前提下可 使得总运费最小？
1.5 表上作业法
最小元素法确定初始基本可行解的步骤：
① 从全部单位运价中找出最低单位运价（若有两个以上最低单位运 价，则可在其中任选其一）。然后比较最低运价所对应的加工厂的日 产量和销地的日销量，并且确定第一笔供销关系。
1.5 运输问题
运输问题（Transportation Problem）： 一类特殊的线性规划问题：它们的约束方程组的系数矩阵 具有特殊的结构，利用这一特点，可能找到比单纯形法更 简便的算法。
运输问题及其数学模型 表上作业法 产销不平衡的运输问题

《运筹学》第三章：运输问题培训课件

《运筹学》第三章：运输问题培训课件

确定初始可行解方法一：西北角 法
门市部 工厂
1
2
3
4 供应总计
9
12
9
6
1
50
7
3
7
7
2
60
6
5
9
11
3
50
需求总计 40 40 60 20
确定初始可行解方法一：西北角 法
门市部 工厂
1
2
3
4 供应总计
9
12
9
6
1
50
40 10
7
3
7
7
2
30 30
60
6
5
9
11
3
30 20
50
需求总计 40 40 60 20
2
34
9 12 9 6
1
40
10
U1
7
3
7
7
2
★
40
20
U2
3
6
5
9
11
40
10
U3
V1 V2 V3 V4
21 (7 6 9) (9 11 7) 5
继续求检验数
门市部
工厂
1
2
3
4
供应总 计
9 12 9 6
1
40 （12） （5）
10
50
7
3
7
7
2
(-5) 40
20 （-2） 60
3
6
计算检验数方法一：闭合回 路法
门市部 工厂
1
9 1
40
7 2
6 3
需求总计 40
2
3

运筹学3.运输问题

运筹学3.运输问题
21
二、初始基可行解的确定
1.最小元素法(就近供应) 就进供应，即从单位运价表中最小的运价开始确定供销 关系，然后次小，一直到求出初始基可行解为止。
例3 销地
产地
B1
B2
B3
B4
ai
3
11
3
10
A1
④③
7
1
A2 ③
9
2
①
84
7
4
10
5
A3
⑥
③
9
Hale Waihona Puke bj365
6 20
Z 31 64 12 43 310 35 86
24
2.伏格尔法（Vogel）
例4
销地 产地
B1
B2
B3
B4 ai
3
A1
②
11
3
⑤
10 7 0 0 0 0
A2
19
①
28
③
4 1111
A3
74
⑥
10 5
③
9 12 - -
bj
36
5
6 20
25 1
3
2 - 1 3 Z 2311 64 53
2
-
1
2
2
-
1
-
3 8 3 5 85
25
在以上两种方法中，有几点需要注意： • 这两种方法得出的解均为初始可行解。 • 一般由伏格尔法得出的解比最小元素法得出的解 更接近最优解。 • 在以上方法过程中，不可同时划去行和列。
26
三、求检验数并进行最优解的判定
1.闭回路法 例5
销地 产地
B1
3 A1
1

第三部分运筹学方法 ppt课件


s.t.
x1 x2 12 x1 3课x件2 18
x1, x2 0
28
• （1）第一步，求可行解域：
• 可行解域是所有满足约束条件的数组，四 个不等式是四个半平面，而可行解域就是 这四个半平面的公共部分。其形状为一个 凸多边形区域，可行解是凸多边形内的一 个点，如图5.1。
课件
29
15
• 定义5.2 某个线性规划模型的全体可行解 组成的集合，称为该线性规划模型的可 行解域。
课件
23
二．线性规划模型的标准型
• 线性规划模型的标准型为：
目标函数 max Z c1x1 c2 x2 cn xn
a11x1 a12 x2 a1n xn b1
约束条件（s.t.）
a21 x1
利润 Z 2x1 5x2 最大；
第三步，确定约束条件：在这个问题中，约束条件是设 备及材料的限制，
设备 A： x1 2x2 8
材料 A： 6x1 24
材料 B： 5x2 15
课件
14
则这一问题的线性规划模型为：
max Z 2x1 5x2
x1 2x2 8
6x1 24 5x2 15
s.t
. x1 , x2 0
课件
15
• 例题5.2（合理下料问题）某厂生产 过程中需要用长度分别为3．1米、 2．5米和1．7米的同种棒料毛坯分 别为200、100和300根，而现在只 有一种长度为9米的原料，问应如何 下料才能使废料最少?
课件
16
解 解决下料问题的关键在于找出所有可能的下料方法
5xx11
x2 x2
10 5
解出
B
点坐标为
5 4
,
15 4

运筹学(第三章)课件


i =1
例1：
某市有三个造纸厂A1,A2和A3，其纸的产量分别为 8，5和9个单位。由各造纸厂到各用户的单位运价 如表所示，请确定总运费最少的调运方案。
销地 产地 A1
A2
A3 销量
B1 3 11 6
4
B2 12 2 7
3
B3 3 5 1
5
B4
产量
4 8
9 5
5 9
6
运筹学(第三章)
销地 产地 A1
A2
A3 销量
B1 4
8
2
8
8
B2
12
8
10
6
5
14
B3
4
3
4
11
8
12
B4
产量
11
16 ②
9
10 ④
6
14
22 ⑥
14
48
①
③
⑤
⑥
8×4+8×12 +6×10+4×3+8×11+14×6= 372（元）
运筹学(第三章)
最小元素法——每次找最小元素
销地 产地 A1
A2
A3 销量
B1 4
2
8
8
8
B2 12
价为 cij (i = 1,2,..., m; n = 1,2,..., n) ，又假设产销是平衡的，即：
m
n
ai = b j ，问应如何安排运输可使总运费最小？
i =1
j =1
运筹学(第三章)
二、运输问题的数学模型
假定 xij 表示由 Ai 到 B j 的运输量，则平衡条件下的运输问题可写出
用表上作业法求解运输问题

运筹学胡运权第3章课件

④
B3 3 2
① ③
B4 10 8 5
③
ai 7 4 9 20
9 4
⑥
10 5 6
6
在调运方案表中，12个格子分成两类： （1） 有数字格（基格） 填写了调运量的格子，对应 解中的基变量。（用白圈表示） （2） 空格 未填写调运量的格子，对应解中的非基变 量，其对应变量在该方案中取值为0。（用蓝圈表示）
③
ai 7 4 9 20
9 4
⑥
10 5 6
6
空格（A1,B1）的闭回路
ú µ ² Ø ú µ Ï Ø A1 A2 A3 bj 3
③
B1 3 1 7
B2 11 9
B3
④ ④ ①
B4 3 2 10
③ ③
ai 10 8 5 7 4 9 20
4
⑥
6
5
6
空格（A2,B2）的闭回路
ú µ ² Ø
ú µ Ï Ø A1 A2 A3 bj
第三章
运输问题
Transportation Problem
§3.1 运输问题的典例和数学模型
例 某食品公司经营糖果业务，公司下设三个加工厂A1、 A2、A3，四个销售门市部B1、B2、B3、B4。已知每天各自的 生产量、销售量及调运时的单位糖果的运输费用等情况。 问：如何调运可使总费用最小？ 生产量：A1——7吨，A2——4吨，A3——9吨
B1 3 1
③
B2 11
B3
④
B4 3 2 10
③ ③
ai 10 8 5 7 4 9 20
9 ① 4
⑥
7 3 6
5
6
空格（A1,B2）的闭回路
ú µ ² Ø
ú µ Ï Ø A1 A2 A3 bj

运筹学课件 第三章

2013-7-12 Introduction to Operations Research Page 7
OR
Graphical Solution
In a similar fashion, the restriction 2x2 < 12 (or, equivalently, x2< 6) implies that the line 2x2=12 should be added to the boundary of the permissible region. The final restriction, 3x1 + 2x2 < 18, provides another line to complete the boundary. The resulting region of permissible values of (x1, x2) , called the feasible region, is shown in Fig. 3.2. The final step is to pick out the point in this feasible region that maximizes the value of Z = 3x1 + 5x2 through trial-and-error procedure.
Chapters 4 and 5 focus on the simplex method. Chapter 6 discusses the further analysis of linear programming problems after the simplex method has been initially applied. Chapter 7 presents several widely used extensions of the simplex method. Chapters 8 and 9 consider some special types of linear programming problems.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

价为 cij (i = 1,2,..., m; n = 1,2,..., n) ，又假设产销是平衡的，即：
m
n
ai = b j ，问应如何安排运输可使总运费最小？
i =1
j =1
运筹学(第三章)
二、运输问题的数学模型
假定 xij 表示由 Ai 到 B j 的运输量，则平衡条件下的运输问题可写出
第三章
运输问题
运筹学(第三章)
主要内容： 第一节 运输问题及数学模型 第二节 用表上作业法求解运输问题 第三节 运输问题的进一步讨论 第四节 运输问题的应用举例
运筹学(第三章)
第一节
运输问题及其数学模型
运筹学(第三章)
一、运输问题的一般提法
运输问题是一种应用广泛的网络最优化模型，其主要目的是为物资调
11
12
12
B4
产量
11
（6）
16
9
-1
10
6
（8）
22
14
48
11 =4432=1 2= 2 1 3 0 4 1 6 1 5 = 1
2= 49 1 1 4 3= 1
存在小于0的检验数，故此运筹基学(可第三行章) 解不是最优解。
注意：
在运输问题中通常目标函数是求最小值，所以 当所有的检验数为正值时，得到最优解。 对于每一个非基变量，在运输表中唯一对应一条 这样的闭回路。
运、车辆调度选择最经济的运输路线。有些问题，比如有 m 台机床加工
n 种零件的问题，工厂的合 理布局问题等, 虽要求与提法不同 , 但经过适
当变化也可以使用本模型求得最优解。
运输问题的一般提法是：
某种物资有 m 个产地 Ai ，产量分别为 ai (i = 1,2,..., m) ，有 n 个销
地 B j ，销量（需求最）分别为 b j ( j = 1,2,..., n) , 已知 Ai 到 B j 的单位运
0x11 x1n 0x21 x2n 0xm1 xmn
= bn
运筹学(第三章)
三、运输问题数学模型的特点
1.平衡条件下的运输问题一定有最优解。 2.运输问题的系数矩阵
x 1x 1 1 2 x 1 n x 2 x 2 1 2 x 2 n x m 1 x m 2 x mn
1
1
1
1
1
如下的线性规划模型：
mn
Minz =
cij xij
i=1 j =1 n
xij = ai
j =1
(i = 1,2,...,m)
m
s.t
xij = bj ( j = 1,2,..., n)
i =1
xij 0
运筹学(第三章)
约束方程即为：
x11 x12 x1n 0x21 0x2n 0x31 0xmn = a1
B2
x12 x22
C12 C22
x m1 b1
Cm1
xm2 b2
Cm2
… …
Bn
产量
x1n x2n
C1n a1 C2n a2
xmn bn
Cmn am
运筹学(第三章)
例子：
某部门有3个生产同类产品的工厂，生产的产品由4个销 售点出售，各工厂的生产量、各销售点的销售量（假定单
位均为吨）以及各工厂到各销售点的单位运价（元/吨）如 下表，要求研究产品如何调运才能使总运费最小。
2
8
8
8
2 2
B2 12
10
5
14
14
5
B3 4
12
3
11
12
1 1
B4
产量 行罚数
11
4
16
9
2
10Leabharlann 682214
48
0 07
1 16 12
3 2
8×2+14×5 +12×4+4×11+2×9+8×6= 244（元）
运筹学(第三章)
二、解的最优性检验 1.闭回路法 2.对偶变量法（位势法）
运筹学(第三章)
闭回路法：
销地 产地 A1
A2
A3 销量
B1 4
2
（8）
8
8
B2 12 10
（14） 5
14
B3 4
（10）
3
（2）
11
12
B4
产量
11
（6）
16
9
10
6
（8）
22
14
48
运筹学(第三章)
销地 产地 A1
A2
A3 销量
B1
4
1
2
（8）
8
10
8
B2
12
2
10
1 （14） 5
14
B3
4
（10）
3
（2）
0x11
0x1n
x21 x22 x2n 0x31 0xmn
= a2
0x11
0x1n
0xm1 n
xm1 xm2 xmn = am
x11 0x12 0x1n x21 0x22 xm1 0xmn = b1
0x11 x12 0x21 x22 0xm1 xm2 0xmn = b2
10
5
14
14
B3
4
10
3
2
11
12
B4
产量
11
6
16 ⑥
9
10 ②
6
8
22 ⑤
14
48
①
④
③
⑥
8×2+14×5 +10×4+2×3+6×11+8×6= 246（元）
运筹学(第三章)
沃格尔法——每次找行罚数和列罚数中最大值所对应的行 或列中最小的元素
销地 产地 A1
A2
A3 销量
列 罚 数
B1 4
运筹学(第三章)
对偶变量法（位势法）：
mn
Minz =
cij xij
i=1 j =1
x11 x12 x1n 0x21 0x2n 0x31 0xmn = a1
A2
A3 销量
B1 4
8
2
8
8
B2
12
8
10
6
5
14
B3
4
3
4
11
8
12
B4
产量
11
16 ②
9
10 ④
6
14
22 ⑥
14
48
①
③
⑤
⑥
8×4+8×12 +6×10+4×3+8×11+14×6= 372（元）
运筹学(第三章)
最小元素法——每次找最小元素
销地 产地 A1
A2
A3 销量
B1 4
2
8
8
8
B2 12
销地 产地 A1
A2
A3 销量
B1 4 2 8
8
B2 12 10 5
14
B3 4 3 11
12
B4
产量
11 16
9 10
6 22
14
48
运筹学(第三章)
一、找出初始基可行解
1.西北角法 2.最小元素法 3.沃格尔法（差值法）
较差 较好
更好
运筹学(第三章)
西北角法——每次找最左上角对应的元素
销地 产地 A1
1
1 1 1
1
1
1
1
1
1
1
1
1(mn)mn
运筹学(第三章)
系数矩阵的特点： （1）约束条件系数矩阵的元素为0或1； （2）约束条件系数矩阵的每一列有两个1元素，
对于变量xij在第i个约束方程中出现一次，在第 m+j个方程中出现第二次； （3）系数矩阵的秩为m+n-1。
运筹学(第三章)
第二节
用表上作业法求解运输问题
运筹学(第三章)
基本思路： （1）找出基本可行解； （2）检验是否为最优解。是，则停止，否，转入
（3）； （3）解的调整。得到一个新的基本可行解，重新
回到步骤二。
所有步骤都在表上进行操作
运筹学(第三章)
运输表
销地 产地 A1
A2
Am 销量
B1
C 11 x 11
C 21 x 21