移相全桥PWM DC-DC变换器的数学建模
- 格式:docx
- 大小:106.54 KB
- 文档页数:3

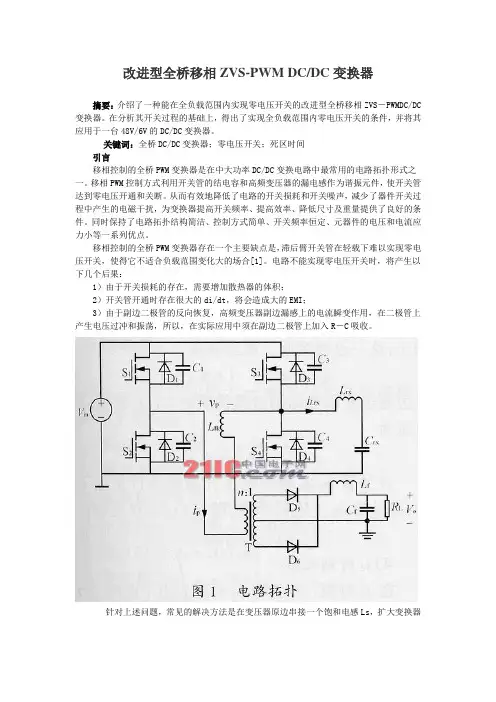
改进型全桥移相ZVS-PWM DC/DC变换器摘要:介绍了一种能在全负载范围内实现零电压开关的改进型全桥移相ZVS-PWMDC/DC 变换器。
在分析其开关过程的基础上,得出了实现全负载范围内零电压开关的条件,并将其应用于一台48V/6V的DC/DC变换器。
关键词:全桥DC/DC变换器;零电压开关;死区时间引言移相控制的全桥PWM变换器是在中大功率DC/DC变换电路中最常用的电路拓扑形式之一。
移相PWM控制方式利用开关管的结电容和高频变压器的漏电感作为谐振元件,使开关管达到零电压开通和关断。
从而有效地降低了电路的开关损耗和开关噪声,减少了器件开关过程中产生的电磁干扰,为变换器提高开关频率、提高效率、降低尺寸及重量提供了良好的条件。
同时保持了电路拓扑结构简洁、控制方式简单、开关频率恒定、元器件的电压和电流应力小等一系列优点。
移相控制的全桥PWM变换器存在一个主要缺点是,滞后臂开关管在轻载下难以实现零电压开关,使得它不适合负载范围变化大的场合[1]。
电路不能实现零电压开关时,将产生以下几个后果:1)由于开关损耗的存在,需要增加散热器的体积;2)开关管开通时存在很大的di/dt,将会造成大的EMI;3)由于副边二极管的反向恢复,高频变压器副边漏感上的电流瞬变作用,在二极管上产生电压过冲和振荡,所以,在实际应用中须在副边二极管上加入R-C吸收。
针对上述问题,常见的解决方法是在变压器原边串接一个饱和电感Ls,扩大变换器的零电压开关范围[2][3]。
但是,采用这一方法后,电路仍不能达到全工作范围的零电压开关。
而且,由于饱和电感在实际应用中不可能具有理想的饱和特性,这将会导致:1)增加电路环流,从而增加变换器的导通损耗;2)加重了副边电压占空比丢失,从而增加原边电流及副边二极管电压应力;3)饱和电感以很高的频率在正负饱和值之间切换,磁芯的损耗会很大,发热严重。
改进型全桥移相ZVS PWMDC/DC变换器是针对上述缺点所提出的一种电路拓扑[4][5][6]。


移相全桥软开关DC—DC变换器的设计与实现作者:邱锴来源:《科学与财富》2016年第16期摘要:详细分析了以电压电流型全桥电路为基础的移相PWM软开关实现方式,并通过附加反激电感与数字化软启动相结合的策略实现了低压侧的软启动。
同时为变换器设计了一套以TMS320F28335为核心的数字控制系统。
实验表明,移相全桥软开关技术能有效减少开关损耗,提升变换器的工作效率。
关键词:DC-DC 变换器;移相PWM控制;软开关引言DC-DC变换器正在朝着小型化、轻量化的方向发展,这就意味着需要工作在更高的频率。
变换器的开关损耗是这一发展方向的难点所在。
软开关(Soft Switching)技术的应用为这一问题提供了良好的解决方法。
它的核心是通过使功率器件工作在零电压开关模式ZVS (Zero-Voltage-Switching)或零电流开关模式ZCS(Zero-Current-Switching),最大限度地降低开关损耗,软化功率器件在开通、关断时的性能,保护开关器件的安全,最终提高变换器的工作效率。
本文详细分析了移相全桥变换器实现软开关的基本原理,通过对拓扑的改进实现了低压侧的软启动。
设计了以DSP28335为核心的数字控制系统。
通过改变对管驱动信号PWM的移相角大小来调节输出电压和输出电流。
1 主电路工作原理移相全桥软开关变换器的基本拓扑结构如图1所示。
高压端Ubus为电压型全桥结构,低压Ubat侧为电流型全桥结构,两端整流/逆变单元的开关管上均并联二极管。
变压器两侧绕组匝数分别为N1、N2,匝比为N1:N2=n;Lr1、Lr2分别为变压器两端的等效漏感或与外串谐振电感之和;电感L处于锂电池端,在本方向处于输出侧时,起到滤波电感平滑纹波的作用。
在本方向处于输入侧时,则起到Boost电感的作用;C1、C2分别为两端滤波电容。
移相全桥软开关的基本原理为:同一个桥臂中的上、下开关管不能同时导通,所以,两管上的驱动信号存在死区,驱动波形一致但相位相隔180度。


I. 引言现代电子设备和电子系统通常由高密度、高速度的电路组成,这样的电路具有低压大电流的特性。
为了带动这样的负载,电源必须能在一个很宽的电流范围内提供稳定的电压,其稳态及暂态的整流特性也必须相当出色。
建模与仿真在现代DC-DC变换器的设计过程中扮演了很重要的角色。
它能让工程师在制作实际电路之前评估变换器的性能。
因此,我们可以在设计之初就发现并更正可能存在的设计缺陷,以提高生产率并节约生产本钱。
DC-DC变换器的建模和仿真在过去的十年里是一个热点[1]。
一般来说,变换器建模方法有两种:开关模型、平均模型。
在开关模型中,模型仿真了变换器的开关动作,仿真波形是包含了开关纹波的波形,这与实际看到的波形很相似。
而平均模型只仿真了变换器的平均特性,仿真波形也是平滑而连续的,这个波形代表了平均值而非实际值。
众所周知,对平均模型进展仿真要比开关模型快。
因此,平均模型常用于变换器动态性能的总体评估。
在过去,平均模型的仿真主要是用SPICE来完成的[2]。
SPICE的缺点在于仿真的对象必须是电路的形式,如果模型原型是复杂的方程式,那么要花费很大的精力将其转换成等效的电路形式。
尽管SPICE的新版本也开场支持建立纯数学模型,但是改善仍然有限。
最近,参考文献[3]介绍了一个不错的可以用在DC-DC变换器建模和仿真方面的工具——SIMULINK[4]。
然而,作者使用的变换器模型是线性化的,在大信号条件下,这个模型的仿真效果并不理想。
为了克制上述缺点,本论文讨论了如何应用SIMULINK在大信号条件下对DC-DC变换器进展平均模型的建模与方针。
本文拓展了文献[3]的研究,在变换器的功率和控制局部使用了非线性化的模型,从而改良了模型在大信号条件下的仿真效果。
下面将分别讨论Buck变换器的非线性化的模型,及相关的三个输出电压控制策略。
A. Buck变换器主电路拓扑Buck变换器主拓扑如图1所示:图1 Buck变换器Fig.1. Buck Converter在电流连续的模式下〔CCM〕——即开关开通的时候,电感电流连续——变换器表现为两个电路状态。

280W移相全桥软开关DC/DC变换器设计摘要:为抑制输出整流二极管反向恢复引起的电压振荡,采用原边带箝位二极管的电路拓扑设计DC/DC变换器。
通过调节移相角调节输出电压,利用开关管的结电容和外接电容以及原边串联电感作为谐振元件,使开关管能进行零电压开通和关断,与传统的移相变换器相比,在变压器原边增加了2个二极管对输出整流二极管进行箝住,实验表明,该方案在实现开关管零电压开通和关断的同时,能够抑制输出整流二极管两端的电压振荡,减小输出整流二极摘要:为抑制输出整流二极管反向恢复引起的电压振荡,采用原边带箝位二极管的电路拓扑设计DC/DC变换器。
通过调节移相角调节输出电压,利用开关管的结电容和外接电容以及原边串联电感作为谐振元件,使开关管能进行零电压开通和关断,与传统的移相变换器相比,在变压器原边增加了2个二极管对输出整流二极管进行箝住,实验表明,该方案在实现开关管零电压开通和关断的同时,能够抑制输出整流二极管两端的电压振荡,减小输出整流二极管的电压应力。
关键词:软开关变换器;寄生振荡;箝住二极管;尖峰电压移相控制的全桥PWM变换器是最常用的中大功率DC/DC变换电路拓扑形式之一。
移相PWM控制方式利用开关管的结电容和高频变压器的漏电感或原边串联电感作为谐振元件,使开关管能进行零电压开通和关断,从而有效地降低了电路的开关损耗和开关噪声,减少了器件开关过程中产生的电磁干扰,为变换器提高开关频率、提高效率、减小尺寸及减轻质量提供了良好的条件。
然而,传统的移相全桥变换器的输出整流二极管存在反向恢复过程,会引起寄生振荡,二极管上存在很高的尖峰电压,需增加阻容吸收回路进行抑制,文献提出了两种带箝位二极管的拓扑,可以很好地抑制寄生振荡。
本文采取文献提出的拓扑结构,设计了一台280 W移相全桥软开关DC/DC变换器,该变换器输入电压为194~310V,输出电压为76V。
1 主电路拓扑及工作过程分析本设计所采用的主电路拓扑如图1所示。


移相全桥ZVSPWMDC/DC变换器的仿真分析作者:龙泽彪施博文来源:《消费导刊·理论版》2008年第17期[摘要]本文首先在研究硬开关的缺陷上,提出软开关技术。
对移相控制ZVS PWM DC/DC 变换器的工作原理进行分析研究的基础上,使用PSpice9.2计算机仿真软件对变换器的主电路进行仿真和分析,验证该新型DC/DC变换器的拓扑结构设计的正确性和可行性。
[关键词]软开关 DC/DC ZVS 移相控制 PSpice9.2作者简介:龙泽彪(1985-),男,湖北仙桃人,贵州大学电气工程学院在读硕士研究生,研究方向:异步电机控制;施博文(1985-),男,贵州大学电气工程学院在读硕士研究生,研究方向:电力电子与电气传动。
一、引言随着新型电力电子器件以及适用于更高频率的电路拓扑和新型控制技术的不断出现,开关电源朝着小型化、高效化、低成本、低电磁干扰、高可靠性、模块化、智能化的方向发展。
硬开关DC/DC变换器在电流连续工作模式下会遇到严重的问题,这一般都与有源开关器件的体内寄生二极管有关,其关断过程中的反向恢复电流产生的电流尖峰对开关器件有极大的危害。
本文在对DC/DC变换器的基本工作原理进行分析、研究的基础上,对已经出现的软开关DC/DC变换器拓扑结构进行分析研究,提出的一种新型的DC/DC变换器的拓扑结构,并进行深入的研究。
二、移相控制ZVS PWM DC/DC全桥变换器的工作原理移相控制ZVS PWM DC/DC全桥变换器(Phase-Shifted zero-voltage-switching PWMDC/DC Full-Bridge Converter,PS ZVS PWM DC/DC FB Converter),是利用变压器的漏感或原边串联的电感和功率管的寄生电容或外接电容来实现开关管的零电压开关,其主电路拓扑结构及主要波形如图1所示。
其中,D1~D4分别是S1~S4的内部寄生二极管,C1~C4分别是S1~S4的寄生电容或外接电容,Lr是谐振电感,它包含了变压器的漏感。

摘要随着电力电子技术的发展,作为电能变换装置的DC-DC变换器的应用越来约广泛,隔离式全桥变换器由于高功率,输入输出电气隔离的优点,应用场合广泛,移相控制使得全桥变换器能够实现ZVS软开关工作,进一步减少的变换器的通态损耗,提高了传输效率,广泛应用于对电能质量有着严格要求的航空航天、电力系统等场合中。
本文首先系统地研究了ZVS全桥变换器地具体工作过程,以半个开关周期为例分析了各开关模态的电流回路和持续时间,研究了在ZVS工作时副边整流侧的二极管换向过程,研究了超前桥臂和滞后桥臂各自实现ZVS的条件。
为了验证ZVS工作过程,在Saber仿真软件中搭建了开环仿真模型对开关管的ZVS工作特性进行了验证。
目前,在采用状态空间平均法对全桥电路建模时通常忽略变压器漏感和输出输出滤波电容的ESR,得到的模型并不能准确反映电路自身特性,本文在此基础上提出了一种改进型的小信号模型,该模型包含变压器漏感,输出电容ESR和变换器工作效率等关键参数,并推导了控制到输出及输出阻抗的传递函数,利用Saber搭建仿真模型对模型准确性进行了验证。
针对移相全桥电路的闭环控制和稳定性进行了研究,对电压控制方式和电流控制方式的原理进行了分析,并研究了闭环系统中补偿器的设计流程。
为了提高控制器的性能,在传统PID控制的基础上研究了模糊自适应PID控制方法在全桥变换器中的应用,根据系统输出电压的偏差和偏差的变化率建立模糊规则,在此基础上设计了模糊自适应PID控制器,从而使得PID控制器参数能够动态调整,系统具有更好的动态特性。
为了验证所设计的Fuzzy PID控制器的性能,在Saber和Matlab/Simulink 中搭建了闭环仿真模型,并于传统的PID控制器进行仿真对比。
通过仿真结果的对比可看出,模糊自适应PID控制方式于传统PID方式相比,系统输出电压具有更好的稳定性和动态特性,而且对系统输入电压和负载电阻的大范围变化具有更好的抗干扰性。

移相全桥ZVZCSDC/DC变换器综述摘要:概述了9种移相全桥ZVZCSDC/DC变换器,简要介绍了各种电路拓扑的工作原理,并对比了优缺点,以供大家参考。
关键词:移相控制;零电压零电流开关;全桥变换器 1概述所谓ZVZCS,就是超前桥臂实现零电压导通和关断,滞后桥臂实现零电流导通和关断。
ZVZCS方案可以解决ZVS方案的故有缺陷,即可以大幅度降低电路内部的循环能量,提高变换效率,减小副边占空比丢失,提高最大占空比,而且其最大软开关范围不受输入电压和负载的影响。
图1 滞后桥臂零电流开关是通过在原边电压过零期间使原边电流复位来实现的。
即当原边电流减小到零后,不允许其继续反方向增长。
原边电流复位目前主要有以下几种方法: 1)利用超前桥臂开关管的反向雪崩击穿,使储存在变压器漏感中的能量完全消耗在超前桥臂的IGBT中,为滞后桥臂提供零电流开关的条件;图2 2)在变压器原边使用隔直电容和饱和电感,在原边电压过零期间,将隔直电容上的电压作为反向阻断电压源,使原边电流复位,为滞后桥臂开关管提供零电流开关的条件; 3)在变压器副边整流器输出端并联电容,在原边电压过零期间,将副边电容上的电压反射到原边作为反向阻断电压源,使原边电流迅速复位,为滞后桥臂开关管提供零电流开关的条件。
图3 2 电路拓扑根据原边电流复位方式的不同,下面列举几种目前常见的移相全桥ZVZCSPWMDC/DC拓扑结构,以供大家参考。
图4 1)NhoE.C. 电路如图1所示[1]。
该电路是最基本的移相全桥ZVZCS变换器,它的驱动信号采用有限双极性控制,从而实现超前桥臂的零电压和滞后桥臂的零电流开关。
这种拓扑结构的缺陷是L1k要折衷选择,L1k太小,在负载电流很小时,超前桥臂不能实现零电压开关;L1k太大,又限制了iL1k的变化速度,从而限制了变换器开关频率的提高。
变换器给负载供电方式是电流源形式,电感L1k电流交流变化,输入电流脉动很大,要求滤波电容很大。
移相全桥PWM 开关电源模型的建立2005-08-291. 降压型电路理想开关模型理想开关模型建模时将开关器件如MOSFET 、IGBT 、VD 等理想化,即设其开通和关断是不需要时间的,并且忽略器件的通态压降和断态电流。
降压型电路开关器件理想化后如图1所示。
该电路工作时电路结构随着开关的开通和关断而变化,其电路方程也是随着开关的通与断而变化的。
因此理想开关模型是时变的。
电路的状态方程可以写成如下形式: 图11111221,[,],[,],(1)i i s i s i A x B u t t t DT x A x B u t t DT t i n ---+∈+⎧=⎨+∈+=⋅⋅⋅⎩ (1)式中,101A C ⎡⎢=⎢⎣ 1/1L RC -⎤⎥⎥-⎦;110B L ⎡⎤⎢⎥=⎢⎥⎣⎦; 201A C⎡⎢=⎢⎣ 1/1L RC -⎤⎥⎥-⎦;200B ⎡⎤=⎢⎥⎣⎦;L C i x u ⎡⎤=⎢⎥⎣⎦;[]i u u =;x 是状态矢量;i L 和u C 是状态变量;ui 是输入电压;D 是占空比。
理想开关模型与实际电路很接近,利用这一模型进行分析得到的结果与实际情况吻合得很好。
但理想开关模型是时变的,获得其解析解比较困难,因此通常用数值的方法来求解。
然而,数值方法总是针对某一特定的问题进行求解,无法获得对某一类控制系统具有普遍意义的结果,因此,常采用其他方法来建立模型进行分析,其中较普遍的状态空间平均法。
2. 状态空间平均模型理想开关模型具有时变性,但在开关处于通态和断态时,其电路结构和状态方程是确定的,也就是定常的。
根据开关处于通态和断态时各自的状态方程及所占时间的比例,将(1)中两个不同时间段的方程按各自的时间比例加权平均,即可得到在一个开关周期内,系统近似的平均状态方程为xAx Bu =+ 12(1)A DA D A =+-12(1)B DB D B =+-即1x C⎡⎢=⎢⎣ 1/1L RC -⎤⎥⎥-⎦x+0D L ⎡⎤⎢⎥⎢⎥⎣⎦u (2) 该状态方程所刻画的模型即为系统的状态空间模型,该模型的方程是定常的,容易得到其解析解,可以获得对一类控制系统具有普遍意义的结果。
移相全桥变换器的建模与仿真由于开关电源是一个线性与非线性相结合的综合系统,给系统的动态研究和设计带来很多不便。
本文主要是用状态空间平均法来进行建立模型,它是由美国加里福尼亚理工学院的R.D.MiddlebrOOk于1976年提出的。
这种方法不仅简化了计算过程,使各种不同结构变换器的解析模型具有了统一的形式,而且操作性更强,工作人员仍可以用波德图(Bode Plot)或者奈奎斯特(Nyquist)定理来对系统进行系统稳定的判定。
1 建模由于移相全桥变换器可由Buck变换器变化而来,首先根据Buck变换器的原理,采用状态空间平均法,建立Buck变换器的小信号模型。
为简单起见,本文简化变换器,使其工作在理想状态,即状态转换是瞬间完成的,在任何时候都只有两种状态存在——导通或关断。
选择电感电流iL和电容电压Uc为状态参量,输出电压Uo和输入电流Is为输出参量,Ui为输入参量,D为晶体管占空比。
如图l所示。
1)变换器工作在CCM状态下,由图2可知,在0≤t≤DTs时间段内,2)变换器工作在DCM状态下,由图3可知,在DTs≤t≤Ts时间段内,二极管的导通占空比为D’=1一D,则基本的状态平均方程组为:将上面各式代入到(10)式并减去式(11)得扰动方程为由于变压器存在漏感Lr,使得移相全桥变换器的有效占空比为Deff,它总小于原边占空比D,则有效占空比的计算如下式:由(16)式可看出,IL、Ui、D的扰动都会使有效占空比Deff发生扰动,而这三种不同的扰动量di、du、dd的表达式分别为从而得到移相全桥变换器的小信号等效电路模型如图4所示。
根据图4导出移相全桥变换器主电路的传递函数,2 仿真本文以一台实验样机的参数为指标,利用MATLAB对系统进行仿真,其参数如下:3 结论通过利用奈奎斯特判据先对系统开环进行仿真,如图5(a)所示,在右半平面内无极点,轨迹与实轴大约为0.678处,(0,j0)不在轨迹范围内,所以该系统开环是稳定的。
随着我国电源行业的发展,在中大功率应用场合,采用PWM 控制技术的移相全桥DC/DC 变换器越来越受到人们的关注,随着PWM 控制技术逐渐向高频化方向发展,全球各大集成电路生产商竞相研制出各种新型的PWM 控制器件,其中TI 公司推出的UCC3895是一款具有代表性的移相全桥控制器件。
该器件既可以工作于电流模式也可以工作于电压模式,又可以为谐振零电压开关提供高频、高效的解决方案,具有广阔的应用前景。
这里基于UCC3895设计了移相全桥DC/DC 变换器的双闭环控制系统,并结合实际应用对该系统进行了实验测试。
1移相全桥DC/DC 变换器闭环系统工作原理移相全桥DC/DC 变换器闭环系统结构框图如图1所示。
直流输入电压经过全桥逆变、高频变压器降压、输出侧整流滤波得到所需的直流电压。
四路PWM 波配置为两组,PWM1、PWM2为一组,用来控制全桥逆变模块的超前臂;PWM3、PWM4为另一组,控制滞后臂。
PWM1与PWM2互补,PWM3与PWM4互补,可通过UCC3895设置合适的死区时间。
该闭环控制电路采用峰值电流模式,外环电压调节器的输出作为电流内环的基准,在电流环中对采样的电流进行斜坡补偿,以保证占空比大于50%的时候,系统仍能稳定工作。
电流环的输出作为调制信号,通过脉宽调制电路、移相电路、隔离驱动电路实现对系统的闭环控制[1]。
2闭环控制电路设计2.1控制模式闭环系统采用恒定导通时刻峰值电流控制方式,可以实现逐个脉冲控制,动态响应速度快,稳定性好,并且易于实现限流及过流保护。
工作原理框图如图2所示。
收稿日期:2009-07-04稿件编号:200907017作者简介:宋杰(1985—),男,四川都江堰人,硕士。
研究方向:现代电子技术及其应用。
移相全桥DC/DC 变换器双闭环控制系统设计宋杰(西南大学工程技术学院,重庆400716)摘要:提出移相全桥DC/DC 变换器闭环系统设计方案,基于PWM 控制器件UCC3895设计一个双闭环控制系统,该系统采用电压外环和电流内环的控制方式,在电压环中引入双零点、双极点的PI 补偿,电流环中引入斜坡补偿,结合实际应用对闭环系统进行实验测试,结果表明所设计的闭环系统动态响应快,稳定性好。
移相全桥移相全桥ZVS 变换器由于其充分利用了电路本身的寄生参数,使开关管工作在软开关状态,降低了开关管的开关噪声和开关损耗,提高了变换器的效率,近年来在中大功率场合得到广泛应用。
随着微处理器价格的不断下降和计算能力的不断提高,采用数字控制已经成为中大功率开关电源的发展趋势,许多数字控制方法相继提出。
但对于DC/ DC 变换器这种强非线性系统,传统的基于线性系统理论的控制方法并不能获得理想的动态特性。
该文在建立移相全桥变换器模型的基础上,提出一种新的模糊PID 预测控制策略,将传统控制方法与智能控制方法相结合,通过模糊控制对传统PID 控制器进行增益调节,同时采用预测控制以补偿数字控制系统中的时延。
这种控制策略比较简单,易于数字控制器的实现,该文采用MA TLAB 方法进行了仿真研究。
2 移相全桥变换器小信号模型的建立一般建立DC/ DC 变换器的小信号模型的方法是状态空间平均法,但对于移相全桥ZVS 变换器来说,用状态空间平均法建模是一项十分复杂的工作。
因为这种变换器具有12种开关状态,因此列写状态空间方程式是一个非常复杂的工作。
根据移相全桥ZVS PWM 变换器源于BUCK 变换器的事实,从电路工作的描述中可以看出变压器副边的有效占空比^off off off d D d =-,变压器原边电压的占空比d 而且依靠输出滤波电感电流L i ,漏感lk L ,输入电压in V 和开关频率s f ,所以移相全桥变换器小信号传递函数也将取决于漏感lk L ,开关频率s f ,滤波电感电流扰动^L i ,输入电压扰动^in V ,和变压器原边占空比扰动^d 等因素。
为了精确地建立移相全桥变换器的动态特性模型,找出lk L ,s f ,^L i ,^in V 和^d 对^off d 的影响是必要的。
这些影响可以加入到PWM BUCK 变换器的小信号电路模型中( 图1),从而获得移相全桥PWM 变换器的小信号模型(图2)。
移相全桥
移相全桥ZVS 变换器由于其充分利用了电路本身的寄生参数,使开关管工作在软开关状态,降低了开关管的开关噪声和开关损耗,提高了变换器的效率,近年来在中大功率场合得到广泛应用。
随着微处理器价格的不断下降和计算能力的不断提高,采用数字控制已经成为中大功率开关电源的发展趋势,许多数字控制方法相继提出。
但对于DC/ DC 变换器这种强非线性系统,传统的基于线性系统理论的控制方法并不能获得理想的动态特性。
该文在建立移相全桥变换器模型的基础上,提出一种新的模糊PID 预测控制策略,将传统控制方法与智能控制方法相结合,通过模糊控制对传统PID 控制器进行增益调节,同时采用预测控制以补偿数字控制系统中的时延。
这种控制策略比较简单,易于数字控制器的实现,该文采用MA TLAB 方法进行了仿真研究。
2 移相全桥变换器小信号模型的建立
一般建立DC/ DC 变换器的小信号模型的方法是状态空间平均法,但对于移相全桥ZVS 变换器来说,用状态空间平均法建模是一项十分复杂的工作。
因为这种变换器具有12种开关状态,因此列写状态空间方程式是一个非常复杂的工作。
根据移相全桥ZVS PWM 变换器源于BUCK 变换器的事实,从电路工作的描述中可以看出变压器副边的有效占空比^off off off d D d =-,变压器原边电压的占空比d 而且依靠输出滤波电感电流L i ,漏感lk L ,输入电压in V 和开关频率s f ,所以移相全桥变换器小信号传递函数也将取决于漏感lk L ,开关频率s f ,滤波电感电流扰动^L i ,输入电压扰动^
in V ,和变压器原边占空比扰动^d 等因素。
为了精确地建立移相全桥变换器的动态特性模型,找出lk L ,s f ,^L i ,^in V 和^d 对^off d 的影响是必要的。
这些影响可以加入到PWM BUCK 变换器的小信号电路模型中( 图1),从而获得移相全桥PWM 变换器的小信号模型(图2)。
我们知道由于谐振电感lk L 和变压器副边整流二级管的影响,移相全桥变换器存在占空比丢失的现象,副边有占空比为:off D D D =-∆ 即()()221/21lk off L o in nL D D I D V T L V T
=---⎡⎤⎣⎦ 移相全桥变换器输出电压增益为:
()()2221/22o lk off L o in in V n L nD nD I D V T L V V T
==---⎡⎤⎣⎦ 其中,n 为变压器副边匝数与原边匝数的比值;L I 为电感电流平均值。
下面通过式(l )来分析对off D 产生影响的因素。
l )占空比扰动^d 对off D 的影响^
d d
由式(l )可得
2^^
^^^^lk o lk d off in nL V n L d d d d D d d V L L =-=-≈ ()lk L L ()3
即占空比扰动^d 对off D 的影响可以近似为^d 。
2)滤波电感电流扰动^L i 对off D 的影响^
i d ^
^d L i in R d i nV =- (4) 这里24d lk s R n L f =,负号表示在原边占空比保持不变的情况下,如果滤波电感电流增
加,off d 将减小,从而降低输出电压,这种影响等效于一个电流负反馈作用。
3)输入电压扰动^in V 对off D 的影响^
v d ()^
^21222o lk L in in D V T nL d I V L V T -⎛⎫=-• ⎪⎝⎭ ()^214o d L in in D V T R I V L nV T
-⎛⎫=-• ⎪⎝⎭ (5) 当()14o L D V T I L -时,则有 ^^2d in L in
R d I V nV =• (6) 把上述结果加到BUCK 变换器的平均小信号电路模型中,也就是通过用off d 的总变化^
off d
来代替在BUCK 变换器小信号模型的^d 从而获得移相全桥ZVS 变换器的小信号模型,如图
2所示。
^^^^off v i d d d d =++ (7)
^i d ,^v d 的作用由两个受控源来表示,^d 的作用由两个独立源来表示。
需要强调的是^
i d ,^v d 来源于电路本身( 即L i 和in V 的扰动)且不被控制电路控制。
从图2 的移相全桥变换器小信号模型中显示BUCK 变换器模型是移相PWM 模型的特例。
由图2 可进行小信号分析,推导出移相全桥ZVS 变换器
的主电路传递函数。
l )图2 所示的输出滤波器的传递函数为:
211o H L s LC s R
=++ (8) 设 21L f s LC s R
∆=++ 则输出滤波器的输入阻抗为:
1f R f Z sRC ∆=+ (9) 输出滤波器的输出阻抗为:
n sL Z f
=∆ (10) 2)控制d 对输出电压o V 的传递函数vd G : 当不考虑输入电压变化量^in V 时,即^
0in V =时,则图2 可变成图3 所示的等效形式。
由图3,可知 ^^^in o i o V nV d d H ⎛⎫=+ ⎪⎝⎭
则由公式(4)、公式(8)可导出: ()()
()()^^^
201
in o in vd d d V V s nV G s s LC s L R R C R R d s '===++++ 上式即为移相全当桥ZVS 变换器的输出电压对输入占空比的传递函数。