第四章答案

第4章 集成运算放大电路自测题一、选择合适答案填入空内。

(1)集成运放电路采用直接耦合方式是因为( C )。

A.可获得很大的放大倍数B.可使温漂小C.集成工艺难于制造大容量电容 (2)通用型集成运放适用于放大( B )。

A.高频信号B.低频信号C.任何频率信号 (3)集成运放制造工艺使得同类半导体管的( C )。

A.指标参数准确B.参数不受温度影响C.参数一直性好 (4)集成运放的输入级采用差分放大电路是因为可以( A )。

A.减小温漂 B.增大放大倍数 C.提高输入电阻(5)为增大电压放大倍数,集成运放的中间级多采用( A )。

A.共射放大电路 B.共集放大电路 C.共基放大电路二、判断下列说法是否正确，用“√”和“×”表示判断结果。

(1)运放的输入失调电压U IO 是两输入端电位之差。

( × ) (2)运放的输入失调电流I IO 是两输入端电流之差。

( √ )(3)运放的共模抑制比cdCMR A A K =。

( √ ) (4)有源负载可以增大放大电路的输出电流。

( √ )(5)在输入信号作用时，偏置电路改变了各放大管的动态电流。

( × ) 三、电路如图T4.3 所示，已知β1＝β2＝β3= 100 。

各管的U BE 均为0.7V , 试求I C 2的值。

解：分析估算如下：21100CC BE BE R V U U I A Rμ--==00202211B B B B I I I I ββββ++==++；0202()1R B B B I I I I ββββ+=+=++图T4.322021C B B I I I ββββ+==⋅+。

比较上两式，得 2(2)1002(1)C R R I I I A ββμβββ+=⋅≈=+++四、电路如图T4.4所示。

图T4.4(1)说明电路是几级放大电路，各级分别是哪种形式的放大电路（共射、共集、差放… … ）;(2)分别说明各级采用了哪些措施来改善其性能指标（如增大放大倍数、输入电阻… … ）。

第四章课后思考题及参考答案1、为什么说资本来到世间，从头到脚，每个毛孔都滴着血和肮脏的东西？[答案要点]资本来到世间，从头到脚，每个毛孔都滴着血和肮脏的东西。

资本主义的发展史，就是资本剥削劳动、列强掠夺弱国的历史，这种剥夺的历史是用血和火的文字载入人类编年史的。

在自由竞争时代，西方列强用坚船利炮在世界范围开辟殖民地，贩卖奴隶，贩卖鸦片，依靠殖民战争和殖民地贸易进行资本积累和扩张。

发展到垄断阶段后，统一的、无所不包的世界市场和世界资本主义经济体系逐步形成，资本家垄断同盟为瓜分世界而引发了两次世界大战，给人类带来巨大浩劫。

二战后，由于社会主义的胜利和民族解放运动的兴起，西方列强被迫放弃了旧的殖民主义政策，转而利用赢得独立和解放的广大发展中国家大规模工业化的机会，扩大资本的世界市场，深化资本的国际大循环，通过不平等交换、资本输出、技术垄断以及债务盘剥等，更加巧妙地剥削和掠夺发展中国家的资源和财富。

在当今经济全球化进程中，西方发达国家通过它们控制的国际经济、金融等组织，通过它们制定的国际“游戏规则”，推行以所谓新自由主义为旗号的经济全球化战略，继续主导国际经济秩序，保持和发展它们在经济结构和贸易、科技、金融等领域的全球优势地位，攫取着经济全球化的最大好处。

资本惟利是图的本性、资本主义生产无限扩大的趋势和整个社会生产的无政府状态，还造成日益严重的资源、环境问题，威胁着人类的可持续发展和生存。

我们今天看到的西方发达资本主义国家的繁荣稳定，是依靠不平等、不合理的国际分工和交换体系，依靠发展中国家提供的广大市场、廉价资源和廉价劳动力，通过向发展中国家转嫁经济社会危机和难题、转移高耗能高污染产业等方式实现的。

资本主义没有也不可能给世界带来普遍繁荣和共同富裕。

2、如何理解商品二因素的矛盾来自劳动二重性的矛盾，归根结底来源于私人劳动和社会劳的矛盾？[答案要点]商品是用来交换的劳动产品，具有使用价值和价值两个因素或两种属性。

第四章存储器管理一、单项选择题1、存储管理的目的是（C ）。

A.方便用户B.提高内存利用率C.方便用户和提高内存利用率D.增加内存实际容量2、在（ A）中，不可能产生系统抖动的现象。

A.固定分区管理B.请求页式管理C.段式管理D.机器中不存在病毒时3、当程序经过编译或者汇编以后，形成了一种由机器指令组成的集合，被称为（B ）。

A.源程序B.目标程序C.可执行程序D.非执行程序4、可由CPU调用执行的程序所对应的地址空间为（D ）。

A.符号名空间B.虚拟地址空间C.相对地址空间D.物理地址空间5、存储分配解决多道作业[1C]划分问题。

为了实现静态和动态存储分配，需采用地址重定位，即把[2C]变成[3D]，静态重定位由[4D]实现，动态重定位由[5A]实现。

供选择的答案：[1]：A 地址空间 B 符号名空间 C 主存空间 D 虚存空间[2]、[3]： A 页面地址 B 段地址 C 逻辑地址 D 物理地址 E 外存地址 F 设备地址[4]、[5]： A 硬件地址变换机构 B 执行程序 C 汇编程序D 连接装入程序E 调试程序F 编译程序G 解释程序6、分区管理要求对每一个作业都分配（A ）的内存单元。

A.地址连续B.若干地址不连续C.若干连续的帧D.若干不连续的帧7、（C ）存储管理支持多道程序设计，算法简单，但存储碎片多。

A.段式B.页式C.固定分区D.段页式8、处理器有32位地址，则它的虚拟地址空间为（ B）字节。

A.2GBB.4GBC.100KBD.640KB9、虚拟存储技术是（ A）。

A.补充内存物理空间的技术B.补充相对地址空间的技术C.扩充外存空间的技术D.扩充输入输出缓冲区的技术10、虚拟内存的容量只受（ D）的限制。

A.物理内存的大小B.磁盘空间的大小C.数据存放的实际地址D.计算机地址字长11、虚拟存储技术与（A ）不能配合使用。

A.分区管理B.动态分页管理C.段式管理D.段页式管理12、（B ）是指将作业不需要或暂时不需要的部分移到外存，让出内存空间以调入其他所需数据。

第四章生产者选择（1）一、选择题1、边际收益递减规律发生作用的前提是（ D ）A．存在技术进步B．生产技术水平不变C．只有一种可变要素的生产D．B与C2、当边际产量大于平均产量时，（ A ）A．平均产量增加B．平均产量减少C．平均产量不变D．平均产量达到最低点3、在规模报酬不变阶段，若劳动的使用量增加10%，资本的使用量不变，则（ D ）A．产出增加10% B．产出减少10% C．产出的增加大于10% D．产出的增加小于10%4、当劳动的（L）总产量下降时，（ C ）A/劳动的平均产量为负B劳动的平均产量为零C劳动的边际产量为负D劳动的边际产量为零5、当劳动的平均产量为正但递减时，劳动的边际产量是（ D ）A正 B 零C负D以上情况都有可能6、下列说法中错误的一种说法是（ B ）A只要总产量减少，边际产量一定是负数B只要边际产量减少，总产量一定也减少C随着某种生产要素投入量的增加，边际产量和平均产量增加到一定程度将趋于下降D边际产量曲线一定在平均产量曲线的最高点与之相交7、当劳动L的边际产量为负时，我们是处于（ C ）A L的第一阶段B L的第二阶段C 的第三阶段D 上述都不是8、等产量曲线是指在这条曲线上的各点代表（D ）A．为生产同等产量投入要素的各种组合比例是不能变化的B．为生产同等产量投入要素的价格是不变的C．不管投入各种要素量如何，产量总是相等的D．投入要素的各种组合所能生产的产量都是相等的9、如果连续地增加某种生产要素，在总产量达到最大时，边际产量曲线（ D ）A. 与纵轴相交B. 经过原点C. 与平均产量曲线相交D. 与横轴相交10、如果等成本线与等产量线没有交点，那么要生产等产量曲线所表示的产量，应该（B ）A. 增加投入B. 保持原投入不变C. 减少投入D. 上述均不正确11、等成本曲线围绕着它与纵轴（Y）的交点逆时针移动表明（ C ）A生产要素Y的价格上升了B生产要素X的价格上升了C生产要素X的价格下降了D生产要素Y的价格下降了四、分析讨论题1、已知生产函数Q=AL1/3K2/3，判断：（1）在短期生产中，该生产函数是否受边际报酬递减规律支配？（提示判断dMP/dL 的值是大于零还是小于零）（2）长期属于规模报酬的哪一种类型？解：（1）因为Q=F(L、K)=AL1/3K2/3，于是有：F(tL、tK)= A(tL)1/3(tK)2/3=t·F(L、K)所以，生产函数Q=AL1/3K2/3属于规模报酬不变的生产函数。

第四章指数函数与对数函数4.1指数P107练习1.用根式的形式表示下列各式（0a>）：（1）12a；（2）34a；（3）35a-；（4）23a-.2.用分数指数幂的形式表示下列各式：（1()0x>；（2()m n>；（3()0p>；（4)3a>.3计算下列各式：（1）323649⎛⎫⎪⎝⎭；（2）；（3）111824a a a-；（4）1123331222x x x--⎛⎫-⎪⎝⎭.P109练习1.计算下列各式：（1）(；（2）233a a a πππ-.2.利用计算工具，探究下列实数指数幂的变化规律：（1）x 取负实数，使得x 的值逐渐增大并趋向于无穷大，计算相应的()2xx R ∈的值，观察变化趋势；（2）x 取正实数，使得x 的值逐渐增大并趋向于无穷大，计算相应的()12xx R ⎛⎫∈ ⎪⎝⎭的值，观察变化趋势.【答案】（1）（2）的值趋向于0.习题4.1P109复习巩固1.求下列各式的值：（1；（2（3（4.【答案】（1100=；（20.1=-；（3|4|4ππ=-=-；（4||x y=-.2.选择题（1）.设0a>，则下列运算中正确的是（）.A.4334a a a= B.2332a a a÷= C.22330a a-= D.144()a a=【答案】D（2）.设0a>，m，n是正整数，且1n>，则下列各式m n a=；01a=；mna-=；正确的个数是（）A.3B.2C.1D.0【答案】解：∵a ＞0，m ，n 是正整数，且n ＞1，∴mn a =显然a 0＝1，正确，而1m n m naa-==m na-=故选：A ．3.填空题（1）在112-⎛⎫- ⎪⎝⎭，122-，112-⎛⎫⎪⎝⎭，12-中最大的数是：___________；【答案】解：11(02--<，1111221(22202--->>>>，∴最大的数是112-⎛⎫⎪⎝⎭．故答案为：112-⎛⎫⎪⎝⎭．（2）按从小到大的顺序，可将π重新排列为_______（可用计算工具）.4.用分数指数幂表示下列各式（式中字母均为正数）：（1；（2；（3）154m .5.计算下列各式（式中字母均为正数）：（1）1373412a a a ；（2）253364a a a ÷；（3）121334x y -⎛⎫ ⎪⎝⎭；（4）21113333243a b a b ---⎛⎫÷- ⎪⎝⎭.6如果在某种细菌培养过程中，细菌每10min 分裂1次（1个分裂成2个），那么经过1h ，1个这种细菌可以分裂成_____________个.【答案】由题：细菌每10min 分裂1次（1个分裂成2个），经过1h 可分裂6次，可分裂成6264=（个）.故答案为：647.（1）已知102,103m n ==，求32210m n-的值；（2）已知23x a =，求33x x x xa aa a--++的值.221x x a a -=-+8.已知11223a a -+=，求下列各式的值：（1）1a a -+；（2）22a a -+.（2）由（1）知17a a -+=，两边平方得2222249,47a a a a --++=∴+=.9.从盛有1L 纯酒精的容器中倒出13L ，然后用水填满；再倒出13L ，又用水填满……（1）连续进行5次，容器中的纯酒精还剩下多少？（2）连续进行n 次，容器中的纯酒精还剩下多少？10.（1）当n =1，2，3，10，100，1000，10000，100000，……时，用计算工具计算()*11nn N n ⎛⎫+∈ ⎪⎝⎭的值；（2）当n 越来越大时，11nn ⎛⎫+ ⎪⎝⎭的底数越来越小，而指数越来越大，那么11nn ⎛⎫+ ⎪⎝⎭是否也会越来越大？有没有最大值？【答案】（1）12331191412;1 2.25;1 2.370412433⎛⎫⎛⎫⎛⎫⎛⎫+=+==+=≈ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭；1010010100111 1.125937;1 1.01 2.704810100⎛⎫⎛⎫+=≈+=≈ ⎪ ⎪⎝⎭⎝⎭；100010011 1.001 2.71691000⎛⎫+=≈ ⎪⎝⎭；100001000011 1.0001 2.718110000⎛⎫+=≈ ⎪⎝⎭；10000010000011 1.00001 2.7183100000⎛⎫+=≈ ⎪⎝⎭.（2）由（1）知，当n 越来越大时，11nn骣琪+琪桫的值也会越来越大，但没有最大值.第四章指数函数与对数函数4.2指数函数4.2.1指数函数的概念P115练习1.下列图象中，有可能表示指数函数的是（）A. B.C. D.【答案】由于0x y a =>（0a >，且1a ≠），所以A ，B ，D 都不正确，故选C.2.已知函数(),y f x x =∈R ，且(0.5)(1)(0.5)(0)3,2,2,,2(0)(0.5)(0.5(1))f f f n f f f f n ====- ，*n ∈N ，求函数()y f x =的一个解析式.【答案】3.在某个时期，某湖泊中的蓝藻每天以6.25%的增长率呈指数增长，那么经过30天，该湖泊的蓝藻会变为原来的多少倍？（可以使用计算工具）【答案】设现在的蓝藻量为a ，经过30天后的蓝藻量为y ，则30(1 6.25%)y a =+，4.2.2指数函数的图象和性质P118练习1.在同一直角坐标系中画出函数3x y =和13xy ⎛⎫= ⎪⎝⎭的图象，并说明它们的关系.2.比较下列各题中两个值的大小：（1）；（2） 3.5 2.30.3,0.3--；（3）0.5 1.21.2,0.5.（2）函数0.3x y =在R 上为减函数，3.5 2.33.5 2.3,0.30.3---<-∴> .（3）0.50 1.200.5 1.21.2 1.21;0.50.51, 1.20.5>=<=∴> .3.体内癌细胞初期增加得很缓慢，但到了晚期就急剧增加，画一幅能反映体内癌细胞数量随时间变化的示意图.【答案】经时间x ，癌细胞数量为y ，图象如图.习题4.2P118复习巩固1.求下列函数的定义域：（1）32xy -=；（2）213x y +=；（3）512xy ⎛⎫= ⎪⎝⎭；（4）10.7x y =.【答案】（1）R ；（2）R ；（3）R ；（4）{|0}x x ≠.2.一种产品原来的年产量是a 件，今后m 年内，计划使产量平均每年比上一年增加%p ，写出年产量y （单位：件）关于经过的年数x 的函数解析式.【答案】()*(1%),x y a p x x m=+∈≤N 3.比较满足下列条件的m ，n 的大小：（1）22m n <；（2）m n 0.20.2<；（3）(01)n m a a a <<<；（4）(1)m n a a a >>.【答案】解：（1）∵函数2x y =在R 上单调递增，且22m n <，∴m n <；（2）∵函数0.2x y =在R 上单调递减，且m n 0.20.2<，∴m n >；（3）∵函数()01xy a a =<<在R 上单调递减，且(01)n m a a a <<<，∴m n >；（4）∵函数()1xy a a =>在R 上单调递增，且(1)m n a a a >>，∴m n >．4.设函数0()(1)xf x Q r =+，且(10)20.23,(11)23.26f f ==.（1）求函数()f x 的增长率r ；（2）求(12)f 的值.【答案】解：（1）由已知得100110(1)20.23(1)23.26Q r Q r ⎧+=⎨+=⎩，解得00.155r Q ≈⎧⎨≈⎩.所以增长率r 约为0.15.（2）由（1）知，()5(10.15)x f x =+，∴1212(12)5(10.15)51.1526.75f =⨯+=⨯≈.P119综合运用5.求下列函数可能的一个解析式：（1）函数()f x 的数据如下表：x012()f x 3.504.205.04（2）函数()g x 的图象如图：【答案】解：（1）设()f x ax b =+.把(0,3.50),(1,4.20)代入得，3.504.20b a b =⎧⎨=+⎩，解得0.703.50a b =⎧⎨=⎩，()0.70 3.50f x x ∴=+为可能的解析式；（2）设()x g x k a =⋅，将(1,2),(1,8)-代入，得6.比较下列各题中两个值的大小：（1）0.83，0.73；（2）0.10.75-，0.10.75；（3） 2.71.01， 3.51.01；（4） 3.30.99， 4.50.99.【答案】（1）由3x y =单调递增，0.80.7>，所以0.830.73>；（2）由0.75x y =单调递减，0.10.1-<，所以0.10.75-0.10.75>；（3）由 1.01x y =单调递增，2.7 3.5<，所以 2.71.01< 3.51.01；（4）由0.99x y =单调递减，3.3 4.5<，所以 3.30.99 4.50.99>.7.当死亡生物组织内碳14的含量不足死亡前的千分之一时，用一般的放射性探测器就测不到碳14了.如果死亡生物组织内的碳14经过九个“半衰期”后，那么用一般的放射性探测器能测到碳14吗？所以能探测到．8.按复利计算利息的一种储蓄，本金为a （单位：元），每期利率为r ，本利和为y （单位：元），存期数为x .（1）写出本利和y 关于存期数x 的函数解析式；（2）如果存入本金1000元，每期利率为2.25%，试计算5期后的本利和.【答案】解：（1）根据题意可得(1)x y a r =+；（2）由（1）可知，当5x =时，51000(1 2.25%)y =+51000 1.022111.5768≈=⨯，∴5期后的本利和约为1117.68元．拓广探索9.已知函数()||12x f x a b ⎛⎫=+ ⎪⎝⎭的图象过原点，且无限接近直线2y =但又不与该直线相交.（1）求该函数的解析式，并画出图象；（2）判断该函数的奇偶性和单调性.【答案】解：（1）由题意知，0,2a b b +==，2a ∴=-，⎩()f x ∴为偶函数，10.已知f (x )=a x，g (x )=1xa ⎛⎫⎪⎝⎭(a >0，且a ≠1).（1）讨论函数f (x )和g (x )的单调性；（2）如果f (x )<g (x )，那么x的取值范围是多少？【答案】（1）当a >1时，f (x )=a x 是R 上的增函数，当0<a <1时，f (x )=a x 是R 上的减函数，当a >1时，x <0；当0<a <1时，x >0.∴当a >1时，x 的取值范围是(,0)-∞；当0<a <1时，x 的取值范围是(0,)+∞.第四章指数函数与对数函数4.3对数4.3.1对数的概念P123练习1.把下列指数式写成对数式，对数式写成指数式：（1）328=；（2）m =；（3）131273-=；（4）3log 92=；（5）lg 2.3n =；（6）31log 481=-.【答案】（1）2log 83=（5） 2.310n=2.求下列各式的值：（1）5log 25；（2）0.4log 1；（3）1ln e；（4）lg 0.001.【答案】（1）2（2）0（3）-1（4）-33.求下列各式中x 的值：（1）13log 3x =-；（2）log 494x =；（3）lg 0.00001x =；（4）ln x =-.4.3.2对数的运算P126练习1.求下列各式的值：（1）()23log 279⨯；（2）lg 5lg 2+；（3）1ln 3ln 3+；（4）33log 5log 15-.【答案】（1）7（2）1（3）0（4）-12.用lg ,lg ,lg x y z 表示下列各式：（1）lg()xyz ；（2）2lg xyz ；（3）3；（4）2lg y z .【答案】解：（1）()lg lg lg lg xyz x y z ++＝；3.化简下列各式：（1）2345log 3log 4log 5log 2⨯⨯⨯；（2）()()48392log 3log 3log 2log 2++.【答案】（1）根据对数的运算性质,结合换底公式,展开化简可得（2）根据对数的运算性质,化简可得()()48392log 3log 3log 2log 2++()()23232232log 3log 3log 2log 2=++习题4.3P126复习巩固1.把下列指数式写成对数式，对数式写成指数式：（1）31x =；（2）146x=；（3）106x =；（4）25x e =；（5）5log 27x =；（6）71log 3x =；（7）lg 0.3x =；（8）x =2.选择题（1）使式子(21)log (2)x x --有意义的x 的取值范围是（）A.2x >B.2x < C.122x << D.122x <<,且1x ≠【答案】D（2）对数lg a 与lg b 互为相反数，则有（）A.0a b +=B.0a b -= C.1ab = D.1a b=【答案】C3.求下列各式的值：（1）1log 2log 2a a+；（2）33log 18log 2-；（3）1lglg 254-；（4）522log 253log 64-；（5）()22log log 16；（6）235log 25log 4log 9⨯⨯.（5）()()42222222log log 16log log 2log 4log 22====；（6）222235233log 25log 4log 9log 5log 2log 3⨯⨯=⨯⨯3258log 2log 5log 3=⨯⨯38log 3818==⨯=4.求满足下列条件的x 的值：（1）ln ln ln x a b =+；（2）lg 3lg lg x n m =-；（3）1log log log 2a a a xbc =-；（4）()234log log log 0x =⎡⎤⎣⎦.【答案】解：（1）ln ln ln x a b=+ ln ln()x ab ∴=，x ab∴=（4）()423log log log 0x =⎡⎤⎣⎦ ，()34log log 1x ∴=，4log 3x ∴=，3464x ∴==P127综合运用5.已知lg 2,lg 3a b ==，求下列各式的值：（1）lg 6；（2）3log 4；（3）2log 12；（4）3lg 2.【答案】lg 2a = ，lg 3b=解：（1）lg 6lg(23)lg 2lg 3a b =⨯=+=+.6.求满足下列条件的各式的值：（1）若3log 41x =，求44x x -+的值；（2）若()3x f x =，求()3log 2f 的值.【答案】解：（1）3log 41x = ，（2）()3x f x = ，()3log 23log 232f ∴==.7.证明：（1）log log log 1a b c b c a ⋅⋅=；（2）m log log na a nb b m=.故log log log =1b a c b c a ⋅⋅.8.某地GDP 的年平均增长率为6.5%，按此增长率，多少年后该地GDP 会翻两番？【答案】设某地GDP 今年为a ，x 年后GDP 会翻两番，则由题知(1 6.5%)2x a a +=，解得 1.065log 211.0067x =≈，故12年后GDP 会翻两番拓广探索9.我们可以把365(11%)+看作每天的"进步”率都是1%，一年后是3651.01；而把365(11%)-看作每天的“落后”率都是1%，一年后是3650.99.利用计算工具计算并回答下列问题：（1）一年后“进步”的是“落后”的多少倍？（2）大约经过多少天后“进步”的分别是“落后”的10倍、100倍、1000倍？∴一年后“进步”的大约是“落后”的1480.7倍∴大约经过230天“进步”的是“落后”的100倍.10.酒驾是严重危害交通安全的违法行为.为了保障交通安全，根据国家有关规定：100mL 血液中酒精含量达到20～79mg 的驾驶员即为酒后驾车，80mg 及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后，其血液中的酒精含量上升到了1mg /mL.如果在停止喝酒以后，他血液中酒精含量会以每小时30%的速度减少，那么他至少经过几个小时才能驾驶？【答案】设他至少经过x 个小时才能驾驶汽车，则()100130%20x-<，∴他至少经过5个小时才能驾驶汽车.第四章指数函数与对数函数4．4对数函数P131练习1.求下列函数的定义域：（1）()ln 1y x =-；（2）1lg y x =；（3）71log 13y x=-；（4）()log 0,1a y a x a =>≠．【答案】（1）(),1-∞（2）()()0,11,+∞2.画出下列函数的图象：（1）lg10x y =；（2）lg 10x y =.【答案】（1）lg10x y x ==，图象如图（2）()lg 010xy x x =>=，图象如图.3.已知集合{1,2,3,4,}A = ，集合{2,4,8,16,}B = ，下列函数能体现集合A 与集合B 一一对应关系的是__________.①2x y =；②2y x =；③2log y x =；④2y x =.【答案】①当x A ∈时，2x y =的值域为B.②当3x =时，3A ∈，但29x B =∉.③当x B ∈时，2log y x =的值域为A.④当3x =时，26y x B ==∉.∴能体现A ，B 对应关系的是①③.故答案为：①③4．4．2对数函数的图象和性质P135练习2.在同一直角坐标系中画出函数3log y x =和13log y x =的图象，并说明它们的关系.【答案】图象如图.相同点：两图象都位于y 轴的右侧，都经过点()1,0，这说明两函数的定义域都是(0,)+∞；两函数的值域都是R .不同点：3log y x =的图象是上升曲线，2.比较下列各题中两个值的大小：（1）lg 0.6,lg 0.8；（2）0.50.5log 6,log 4；（3）log 5,log 7m m .【答案】（1）lg y x =为增函数，0.60.8,lg 0.6lg 0.8<∴< .（2）0.5log y x =为减函数，0.50.564,log 6log 4>∴< .（3）当1m >时，log m y x =为增函数.57,log 5log 7m m <∴< .当01m <<时，log m y x =为减函数.57,log 5log 7m m <∴> .3.某地去年的GDP （国内生产总值）为3000亿元人民币，预计未来5年的平均增长率为6.8%.（1）设经过x 年达到的年GDP 为y 亿元，试写出未来5年内，y 关于x 的函数解析式；（2）经过几年该地GDP 能达到3900亿元人民币？【答案】（1）由题意3000(1 6.8%)(05)x y x =+.∴约经过4年该地GDP 能达到3900亿元人民币.4．4．3不同函数增长的差异P139练习1.三个变量123,,y y y 随变量x 变化的数据如下表：x0510152025301y 513050511302005313045052y 59016202916052488094478401700611203y 5305580105130155其中关于x 呈指数增长的变量是_____【答案】指数型函数呈“爆炸式”增长.从表格中可以看出，三个变量，1y ，2y ，3y 的值随着x 的增加都是越来越大，但是增长速度不同，相比之下，变量2y 的增长速度最快，可知变量2y 关于x 呈指数型函数变化.故答案为：2y 2.（1）（2）（3）分别是函数3x y =和5y x =在不同范围的图象，借助计算工具估算出使35x x >的x 的取值范围（精确到0.01）.（1）（2）（3）【答案】记()35x f x x =-，计算(0)10=>f ，(0.3)0.110f =-<，(0.15)0.4290f =>，(0.225)0.1550f =>，(0.263)0.020f =>，(0.282)0.0470f =-<，(0.272)0.0110f =-<，0.2720.2630.090.1-=<，近似解取0.27，(2)10,(3)120,f f =-<=>(2.5) 3.0880f =>，(2.25)0.5950f =>，(2.125)0.3000f =-<，(2.188)0.1250f =>，2.125 2.1880.0070.01-=<，近似解取2.19，故估算范围是(,0.27)(2.19,)-∞+∞ 3.如图，对数函数lg y x =的图象与一次函数()y f x =的图象有A ，B 两个公共点，求一次函数()y f x =的解析式.【答案】由题意(1,0),(2,lg 2)A B .设()f x ax b =+，则0lg 2lg 22lg 2a ba ab b ⎧=+=⎧⇒⎨⎨=+=-⎩⎩.()(lg 2)lg 2(lg 2)(1)f x x x ∴=-=-4.函数()y f x =的图象如图所示，则()y f x =可能是（）A.11,(0,)y x x -=-∈+∞B.31,(0,)22xy x ⎛⎫=-∈+∞ ⎪⎝⎭C.ln y x=D.1,(0,)y x x =-∈+∞【答案】由图象过()1,0知B 不正确，由()31f >知A 不正确，由图象为曲线知D 不正确，所以应选C.习题4．4P140复习巩固1.求下列函数的定义域:(1)y =;(2)y =.【答案】解:(1)由条件知0x >,故定义域为(0,)+∞.2.比较满足下列条件的两个正数m ,n 的大小:(1)33log log m n <;(2)0.30.3log log m n <;(3)log log (01)a a m n a <<<;(4)log log (1)a a m n a >>.【答案】(1)因为3log y x =为增函数,故m n <；(2)因为0.3log y x =为减函数,故m n >；(3)因为()log ,01a y x a =<<为减函数,故m n >；(4)因为()log ,1a y x a =>为增函数,故m n >；3.在不考虑空气阻力的情况下，火箭的最大速度v （单位：m /s ）和燃料的质量M （单位：kg ）、火箭（除燃料外）的质量m （单位：kg ）的函数关系表达式为2000ln 1Mv m ⎛⎫=+⎪⎝⎭.当燃料质量是火箭质量的多少倍时，火箭的最大速度可以达到12km /s ？61e -倍．4.函数2log y x =，5log y x =，lg y x =的图象如图所示，（1）试说明哪个函数对应于哪个图象，并解释为什么；（2）以已有图象为基础，在同一直角坐标系中画出12log y x =，15log y x =，110log y x =的图象；（3）从（2）的图中你发现了什么？【答案】【小问1详解】当底数大于1时，在直线1x =的右侧，底数越大，函数图象越靠近x 轴，所以①对应函数lg y x =，②对应函数5log y x =，③对应函数2log y x =.【小问2详解】.【小问3详解】从（2）的图中发现25log ,log ,lg y x y x y x ===的图象分别与5.大西洋鲑鱼每年都要逆流而上2000m ,游回产地产卵,研究链鱼的科学家发现链鱼的游速,(单位:/m s )可以表示为31log 2100O v =,其中O 表示鱼的耗氧量的单位数.(1)当一条鱼的耗氧量是2700个单位时,它的游速是多少?(2)计算一条鱼静止时耗氧量的单位数.6.在2h 内将某种药物注射进患者的血液中，在注射期间，血液中的药物含量呈线性增加；停止注射后，血液中的药物含量呈指数衰减.下面能反映血液中药物含量Q 随时间t 变化的图象是（）A. B.C. D.【答案】解：在在2h 内，血液中的药物含量呈线性增加，则第一段图象为线段，且为增函数，排除A ，D ，停止注射后，血液中的药物含量呈指数衰减，排除C ．能反映血液中药物含量Q 随时间t 变化的图象是B ．P140综合运用7.判断下列各对函数是否互为反函数,若是,则求出它们的定义域和值域:(1)ln ,x y x y e ==;(2)1log ,xa y x y a ⎛⎫=-= ⎪⎝⎭.【答案】(1)求ln y x =的反函数有ln x x y y e =⇒=.故ln ,x y x y e ==,且互为反函数.ln y x =的定义域为(0)+∞，,值域为R .x y e =的定义域为R ,值域为(0)+∞，.互为反函数.8.设()y f x =表示某学校男生身高为x cm 时平均体重为y kg ,(1)如果函数()y f x =的反函数是()y g x =,那么()y g x =表示什么?(2)如果(170)55f =,那么求(55)g ,并说明其实际意义.【答案】(1)因为()y f x =表示某学校男生身高为x cm 时平均体重为y kg ,则其反函数自变量与因变量交换,即()y g x =表示该校男生体重为x kg 时,平均身高为y cm .(2)由(1)可得(55)170g =.且(170)55f =说明该校某男生身高为170cm 时,体重为55kg .(55)170g =说明该校某男生体重为55kg 时,身高为170cm .9.某地由于人们健康水平的不断提高,某种疾病的患病率正以每年15%的比例降低,要将当前的患病率降低一半,需要多少年?【答案】解:设今年的患病率为a ,经x 年后的患病率为当前的一半.则10.声强级1L (单位:dB )由公式11210lg 10I L -⎛⎫= ⎪⎝⎭给出,其中I 为声强(单位:2/W m ).(1)一般正常人听觉能忍受的最高声强为21/W m ,能听到的最低声强为12210/W m -.求人听觉的声强级范围.(2)平时常人交谈时的声强约为6210/W m -,求其声强级.因此人听觉的声强级范围为0120dB dB -.11.假设有一套住房从2002年的20万元上涨到2012年的40万元.下表给出了两种价格增长方式，其中1P 是按直线上升的房价，2P 是按指数增长的房价，t 是2002年以来经过的年数.t 051015201/P 万元20402/P 万元2040（1）求函数1()P f t =的解析式;（2）求函数2()P f t =的解析式；（3）完成上表空格中的数据，并在同一直角坐标系中画出两个函数的图像，然后比较两种价格增长方式的差异.【答案】（1）因为1P 是按直线上升的房价,设(),0f t kt b t =+≥,由(0)020f k b =⨯+=,(10)1040f k b =⨯+=,可得2,2k b ==,即1220,0P t t =+≥.（2）因为2P 是按指数增长的房价,设0(),0tg t a a t =≥,由01000(0)20,(10)40g a a g a a ====,则表格如下:根据表格和图像可知:房价按函数1()P f t =呈直线上升,每年的增加量相同,保持相同的增长速度；按函数2()P g t =呈指数增长,每年的增加量越来越大,开始增长慢,然后会越来越快,但保持相同的增长比例.P141拓广探索12.已知1log 12a <，112a⎛⎫< ⎪⎝⎭，121a <求实数a 的取值范围.13.比较下列各题中三个值的大小:(1)0.20.30.4log 6,log 6,log 6;(2)234log 3,log 4,log 5.且lg 0.2lg 0.3lg 0.40<<<,故0.20.30.4log 6log 6log 6>>23log 3log 4∴>同理可证35234log 4log 5,log 3log 4log 5>∴>>.第四章指数函数与对数函数4.5函数的应用（二）4.5.1函数的零点与方程的解P144练习1.图（1）（2）（3）分别为函数()y f x =在三个不同范围的图象.能否仅根据其中一个图象，得出函数()y f x =在某个区间只有一个零点的判断？为什么？（1）（2）（3）【答案】解：不能，如仅依据图（1）易得出()f x 在（-200，200）内仅有一个零点的错误结论，要证明函数在某区间上只有一个零点，除证明该函数在区间端点的函数值异号外，还需证明该函数在该区间上是单调的.2.利用计算工具画出函数的图象，并指出下列函数零点所在的大致区间：（1）()335f x x x =--+；（2）()()2ln 23f x x x =--；（3）()144x f x e x -=+-；（4）()()()()3234f x x x x x =+-++.【答案】作出函数图象（如图）.因为(1)10f =>， 1.5) 2.8750f =-<(，所以3()35f x x x =--+在区间（1，1.5）上有一个零点.又因为()f x 是(,)-∞+∞上的减函数.所以3()35f x x x =--+在(,)-∞+∞上有且仅有一个零点.作出函数图象（如图），因为(3)0f <，(4)0f >，所以()2ln(2)3f x x x =--在区间（3，4）上有一个零点，又因为()2ln(2)3f x x x =--在(2,)+∞上是增函数，所以()f x 在(2,)+∞上有且仅有一个零点作出函数图象（如图），因为(0)0f <，(1)0f >，所以1()44x f x x -=+-e在区间（0，1）上有一个零点.又因为1()44x f x x -=+-e 在(,)-∞+∞上是增函数，所以()f x 在(,)-∞+∞上有且仅有一个零点.（4）作出函数图象（如图）.因为(4)0f -<，(3)0f ->，(2)0f -<，(2)0f <，(3)0f >，所以()3(23)(4)f x x x x x =+-++)(在（-4，-3），（-3，-2），（2，3）上各有一个零点.4.5.2用二分法求方程的近似解P146练习1.借助信息技术,用二分法求函数()321.10.9 1.4f x x x x =++-在区间(0,1)内零点的近似值(精确度为0.1)【答案】解:利用计算机软件画出函数图象如图所示：由题设可知()0 1.40f =-<,()1 1.60f =>,于是()()010f f ⋅<.又因为函数()f x 在()0,1内单调递增,所以函数()f x 在区间()0,1内有一个零点.下面用二分法求函数()321.10.9 1.4f x x x x =++-在区间()0,1内的零点取区间()0,1的中点00.5x =,用计算器可算得()0.50.55f =-.因为()()0.510f f ⋅<,所以()00.51x ∈，.再取区间()0.5,1的中点2075x =,用计算器可算得()0.750.32f ≈.因为()()0.50.750f f ⋅<,所以()00.50.75x ∈，.同理可得()00.6250.75x ∈，,()00.6250.6875x ∈，.2.借助信息技术,用二分法求方程x=3-lgx 在区间(2,3)内的近似解(精确度为0.1).【答案】解:原方程即lg 30x x +-=,令()13f x x gx =+-,函数图象如图所示：用计算器可算得()20.70f ≈-,()30.48f ≈,于是()()230f f ⋅<,又因为函数()f x 在()2,3内单调递增,所以这个方程在区间()2,3内有一个解.下面用二分法求方程3x lgx =-在区间()2,3的近似解.取区间()2,3的中点1 2.5x =,用计算可算得()2.50.10f ≈-.因为()()2.530f f <,所以()0 2.53x ∈，.再取区间()2.5,3的中点2275x =,用计算器可算得()2.750.19.f ≈因为()()2.5 2.750f f ⋅<,所以0 2.52.75x ∈（，）.同理可得()0 2.52.625x ∈，,()0 2.56252.625x ∈，.所以原方程的近似解可取为2.5625.4.5.3函数模型的应用P150练习1.已知1650年世界人口为5亿，当时人口的年增长率为0.3%；1970年世界人口为36亿，当时人口的年增长率为2.1%．（1）用马尔萨斯人口模型计算，什么时候世界人口是1650年的2倍?什么时候世界人口是1970年的2倍？（2）实际上，1850年以前世界人口就超过了10亿；而2004年世界人口还没有达到72亿．你对同样的模型得出的两个结果有何看法？【答案】解：（1）设1650年后n 年，人口是1650年的2倍，即有5(10.3%)10n +=，两边取常用对数，可得 1.0032nlg lg =，即有36(1 2.1%)72m +=，两边取常用对数，可得 1.0212mlg lg =，则有1881年世界人口是1650年的2倍，2003年世界人口是1970年的2倍；（2）实际上，1850年以前世界人口就超过了10亿；而2003年世界人口还没有达到72亿．由此看出，此模型不太适宜估计跨度时间非常大的人口增长情况．2.在一段时间内，某地的野兔快速繁殖，野兔总只数的倍增期为21个月，那么1万只野兔增长到1亿只野兔大约需要多少年？所以大约需要23年.3.1959年，考古学家在河南洛阳偃师市区二里头村发掘出了一批古建筑群，从其中的某样本中检测出碳14的残余量约为初始量的62.76%，能否以此推断二里头遗址大概是什么年代的？（碳14的半衰期为5730年）而385119591892-=.所以大概是公元前1892年的.P154练习1.某地今年1月，2月，3月患某种传染病的人数分别为52，61，68为了预测以后各月的患病人数，甲选择了模型2y ax bx c =++，乙选择了模型x y pq r =+，其中y 为患病人数，x 为月份数，,,,,,a b c p q r 都是常数。

语言学第四章课后答案1、“桌子”，“书包”都属于名词，这体现了语法的什么性质（）。

[单选题] *A.抽象性(正确答案)B.递归性C.系统性D.稳定性答案解析：“桌子”、“书包”等词语，虽然意思不同，但根据某种共同特点——大都能受数量词的修饰，就可以建立“名词”这个类：这就是词的用法对语法单位类别的抽象。

这体现了语法的抽象性。

2、语法规则的“系统性”是指（）。

[单选题] *A.对语言的结构和成分进行类的概括B.相同规则可在一个结构里重复使用C.语法规则之间可以相互推导和解释(正确答案)D.语法规则的发展变化过程十分缓慢答案解析：所谓“系统”，指的是语法规则具有推导性和解释性。

3、“三思而后行”在今天读来依旧朗朗上口，体现了语法的什么性质（）。

[单选题] *A.抽象性B.递归性C.系统性D.稳定性(正确答案)答案解析：“三思而后行”这句话产生在古代，现在依旧适用，体现语法的稳定性。

4、下列不属于共时语法的是（）。

[单选题] *A.现代汉语语法B.先秦汉语语法C.汉语语法的演化(正确答案)D.近代汉语语法答案解析：共时语法指的是从某一时期存在的语法现象横向地静态地研究语法。

因此A、B、D选项都属于共时语法。

汉语语法的演化属于历时语法的体现。

5、以下关于“教学语法和信息语法”的内容说法有误的一项是（）。

[单选题] *A.这是根据语法研究的用途区分的语法B.教学语法研究的结果面对的是人，或者说这种语法系统要充分考虑人的特点C.信息语法也叫“计算机语法”D.语法规则体系，方便计算机处理信息。

其特点是精确可靠，定义和规则具有可推导性和可开发性(正确答案)答案解析：教学语法和信息语法是根据语法研究的用途区分的语法。

教学语法研究的结果面对的是人，或者说这种语法系统要充分考虑人的特点；信息语法也叫“计算机语法”，其研究结果服务的是机器，即建立一套可以自动识别和操作的语法规则体系，方便计算机处理信息。

其特点是精确可靠，定义和规则具有可推导性和可验证性。

第四章社会主义改造的理论一、单项选择题1. 中华人民共和国的成立，标志着中国已从半殖民地半封建社会进入到A. 资本主义社会B. 新民主主义社会C. 社会主义社会D. 共产主义社会2. 建国初期，建立社会主义国营经济的主要途径是A. 没收帝国主义在华企业B. 没收官僚资本C. 赎买民族资产阶级的财产D. 剥夺地主阶级土地和财产3. 1950年6月，中央人民政府颁布的土地法是A.《中国土地法大纲》B.《中华人民共和国土地法》C.《中国土地改革法》D.《中华人民共和国土地改革法》4. 1951年至1952年“五反”运动开展的领域是A. 国营企业B. 私营企业C. 党政机关D. 合作社5. 党在过渡时期的总路线和总任务是A. 无产阶级领导的，人民大众的，反对帝国主义、封建主义、官僚资本主义的革命B. 在一个相当长的时期内，逐步实现国家的社会主义工业化，并逐步实现国家对农业、手工业和资本主义工商业的社会主义改造C. 鼓足干劲，力争上游，多快好省地建设社会主义D. 以经济建设为中心，坚持四项基本原则，坚持改革开放，自力更生，艰苦创业，为把我国建设成富强、民主、文明的社会主义现代化国家而奋斗6. 1953年9月，毛泽东在对民主党派和工商界部分代表讲话时指出：改造资本主义工商业和逐步完成社会主义过渡的必经之路是A. 剥夺资本家的财产B. 排挤私营工商业C. 国家资本主义D. 保护民族工商业7、我国对资本主义工商业的社会主义改造采取的政策是A. 经销代销B. 和平赎买C. 统购包销D. 加工订货8、1956年我国在生产资料所有制的社会主义改造基本完成后，开始进入A．新民主主义时期 B．国民经济恢复时期C．从新民主主义向社会主义过渡时期 D．全面建设社会主义时期9. 中国共产党七届三中全会提出的中心任务是A. 消灭国民党反动派残余势力B. 争取国家财政经济状况的好转C. 在新解放区完成土地改革D. 合理调整工商业10. 中国在对资本主义改造中在利润上采取的是A. 统筹兼顾B. 劳资两利C. 公私兼顾D. 四马分肥11. 在农业社会主义改造中拥有社会主义性质的是A. 临时互助组B. 初级社C. 高级社D. 人民公社12. 建国之初，在土地改革中对待富农的土地采取的政策是A. 征收富农的多余土地B. 消灭富农经济C. 保存富农经济D. 限制富农经济13. 社会主义改造的实质是A. 消灭生产资料私有制B. 消灭生活资料私有制C. 消灭资本主义经济D. 消灭个体经济14. 社会主义过渡时期总路线错误的说法是A. 实现社会主义工业化、农业手工业和资本主义工商业的社会主义改造B. 过渡时期结束的标志是社会主义改造结束C. 以单一的社会主义公有制和计划经济体制为目标D. 以中国特色社会主义为目标15、社会主义改造中最具有中国特色、对社会主义学说贡献最大的是A．对资本主义工商业的社会主义改造B．对农业的社会主义改造C．对手工业的社会主义改造D．社会主义工业化道路16．在农业社会主义改造中建立的初级农业生产合作社属于（2004年科研题）A. 新民主主义性质B. 社会主义萌芽性质C. 半社会主义性质D. 社会主义性质17. 1957年，毛泽东在《关于正确处理人民内部矛盾的问题》中指出，在我国，工人阶级与民族资产阶级的矛盾属于人民内部的矛盾。

习题4.1选择填空1、选用差分放大电路的原因是 A 。

A 、克服温漂B 、 提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ，将使电路的 B 。

A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。

4、设差放电路的两个输入端对地的电压分别为v i1和v i2，差模输入电压为v id ，共模输入电压为v ic ，则当v i1=50mV ，v i2=50mV 时，v id =_0mV __，v ic =_50mV __；当v i1=50mV ，v i2=-50mV 时，v id =_100mA __，v ic =_0mA__；当v i1=50mV ，v i2=0V 时，v id =_50mV __，v ic =_25mA __。

5、电流源常用于放大电路，作为_A ___（A.有源负载，B.电源，C.信号源），使得放大倍数__A __（A.提高，B.稳定）。

6、电压放大电路主要研究的指标是 a 、 b 、 c ；功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、（a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗）7、功率放大电路中，___甲类____功率放大电路导通角最大；_____乙类___功率放大电路效率较高。

（甲类、乙类、甲乙类） 8、甲类功放效率低是因为 B 。

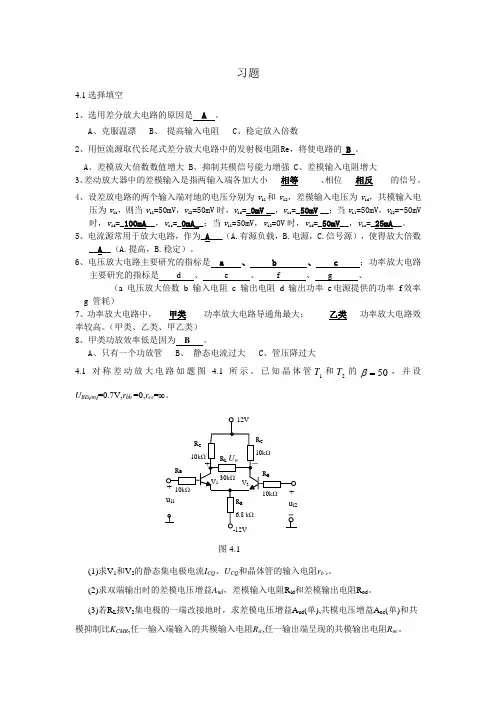
A 、只有一个功放管B 、 静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。

已知晶体管1T 和2T 的50=β，并设U BE (on )=0.7V,r bb ’=0,r ce =∞。

(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。

(2)求双端输出时的差模电压增益A ud ，差模输入电阻R id 和差模输出电阻R od 。

第四章的习题及答案4-1 设有一台锅炉，水流入锅炉是之焓为62.7kJ ·kg -1，蒸汽流出时的焓为2717 kJ ·kg -1，锅炉的效率为70％，每千克煤可发生29260kJ 的热量，锅炉蒸发量为4.5t ·h -1，试计算每小时的煤消耗量。

解：锅炉中的水处于稳态流动过程，可由稳态流动体系能量衡算方程：Q W Z g u H s +=∆+∆+∆221体系与环境间没有功的交换：0=s W ，并忽 动能和位能的变化， 所以： Q H =∆设需要煤mkg ，则有：%7029260)7.622717(105.43⨯=-⨯m解得：kg m 2.583=4-2 一发明者称他设计了一台热机，热机消耗热值为42000kJ ·kg -1的油料0.5kg ·min -1,其产生的输出功率为170kW ，规定这热机的高温与低温分别为670K 与330K ，试判断此设计是否合理？解：可逆热机效率最大，可逆热机效率：507.06703301112max =-=-=T T η 热机吸收的热量：1m in210005.042000-⋅=⨯=kJ Q热机所做功为：1m in 102000m in)/(60)/(170-⋅-=⨯-=kJ s s kJ W该热机效率为：486.02100010200==-=Q W η 该热机效率小于可逆热机效率，所以有一定合理性。

4-3 1 kg 的水在1×105 Pa 的恒压下可逆加热到沸点，并在沸点下完全蒸发。

试问加给水的热量有多少可能转变为功？环境温度为293 K 。

解：查水蒸气表可得始态1对应的焓和熵为：H 1＝83.93kJ/kg, S 1=0.2962kJ/kg.K 末态2对应的焓和熵为：H 2＝2675.9kJ/kg, S 2=7.3609kJ/kg.K)/(0.259293.839.267512kg kJ H H Q =-=-=)/(0.522)2962.03609.7(15.2930.25920kg kJ S T H W sys id =-⨯-=∆-∆=4-4如果上题中所需热量来自温度为533 K 的炉子，此加热过程的总熵变为多少？由于过程的不可逆性损失了多少功？ 解：此时系统的熵变不变)./(0647.7K kg kJ S sys =∆炉子的熵变为)./(86.45330.2592K kg kJ T H T Q S sur -=-=∆-==∆ )./(205.286.40647.7K kg kJ S t =-=∆ )/(0.646205.215.2930kg kJ S T W t l =⨯=∆=4-5 1mol 理想气体，400K 下在气缸内进行恒温不可逆压缩，由0.1013MPa 压缩到1.013MPa 。