excel的方差分析与实例应用

如何在Excel中使用ANOVA函数进行方差分析方差分析是一种常用的统计方法，用于比较两个或多个样本均值之间的差异。

在Excel中，我们可以通过使用ANOVA函数来进行方差分析。

本文将介绍如何在Excel中使用ANOVA函数进行方差分析，并提供实例说明。

1. 准备数据首先，我们需要准备待分析的数据。

例如，我们有一个实验，采集了三组数据，每组数据包含10个观测值。

将这些数据依次输入Excel的工作表，确保每组数据都位于不同的列中。

数据输入完成后，我们可以开始进行方差分析的计算。

2. 使用ANOVA函数在Excel中，ANOVA函数用于计算方差分析的结果。

它需要输入两个参数：范围和标签。

范围是要进行方差分析的数据范围，标签是用于区分不同数据组的标签。

在我们的例子中，假设三组数据分别位于A1:A10、B1:B10和C1:C10范围中，并将标签分别输入D1:D10、E1:E10和F1:F10范围中。

我们在G列中输入以下公式：=ANOVA(A1:A10,C1:C10,E1:E10)。

按下回车键后，Excel将计算出方差分析的结果。

3. 解读分析结果方差分析的计算结果将显示在Excel单元格中。

通过观察Excel的输出，我们可以得到以下信息：- 总体平均值（Mean Square Total）：计算所有数据的均值。

- 组间平均值（Mean Square Factor）：计算各组数据的均值。

- 组内平均值（Mean Square Error）：计算各组数据的方差。

- F值（F Value）：计算组间均值和组内均值之比。

- P值（P Value）：用于判断差异的显著性水平。

4. 判断显著性根据分析结果中的P值，我们可以判断数据之间的差异是否显著。

通常，当P值小于0.05时，我们可以认为差异是显著的。

在Excel中，我们可以使用条件格式来使P值小于0.05的单元格自动变色，以便更方便地进行观察和判断。

5. 结论通过Excel的ANOVA函数，我们可以很方便地进行方差分析，并得到有关数据差异的信息。

精心整理第10章 Excel软件在概率统计中的应用10.1 中文Excel的基本介绍Excel是一个功能多、技术先进、使用方便的表格式数据综合管理和分析系统，它采用电子表格的形式进行数据处理，工作简单明了，提供了丰富的函数，可以进行为列标，用A,B,…,Z,AA,AB, …表区左边一列为行号，用1,2,3，…容量，列数最多可为16384A列第1行。

单元格区域则规定为矩形，10-1，A1和E4例如：“”.工作表隶属于工作簿，一个工作簿最多可由10-11）Excel2003版，使用“插入”菜单—“函贴函数”对话框；若是Excel2010版，使用“公式”菜单—“插入函数”选项。

图10-22）点击“函数”选项后，将出现如图10-3所示的对话框。

图10-33）在“选择类别”列表中选择“统计”，如图10-4，然后在“函数名”列表中选择相应的函数，如选中函数“AVERAGE”,点击“确定”按钮，出现输入数据或单元格范围的对话框；如图10-5图10-4 图10-54)输入数据或单元格范围,点击“确定”按钮，在函数值存放的单元格即计算出（返回）函数值。

注：若对某函数的使用不太熟悉，可以点击图10-5左下方的“有关该函数的帮助”按钮，即可获得帮助。

若为Excel2003版本：12）在对话框中选定“分析工具库”3），如图10-7410-8所示的对话框.1）首先点击自定义快速访问工具栏中的其他命令（M）…，如图10-9所示：图10-92）当出现如图10-10所示的Excel选项后，选择“加载项”。

图10-103）当出现如图10-11所示的窗口后，选择“分析工具库”，然后点击下方的按钮“转到（G）…”,则将出现与图10-6一样的窗口，其他就和2003版一致了。

当加载完成后，就会在“数据”菜单中看见“数据分析”工具条了。

图10-11在图10-8的对话框中共有19个模块，它们分别属于5大类：1.基础分析：（1）随机数发生器；（2）抽样；（3）描述统计；（4）直方图；（5）排位与百分比排位。

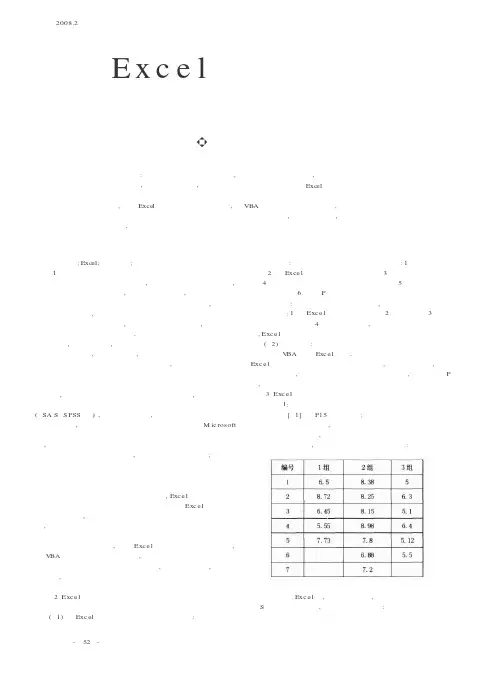
关键词:Exc el;体育统计;方差分析1、前言体育教学实验与分析过程中,对多个教法之间的比较,如果采用两两比较的方法,检验方法很繁琐,此时需要用到方差分析的方法。

比如不同的教师采用不同的教法,经过一个学期的教学后,各教学组学生的成绩不相等。

需要检验学生之间平均成绩有无差异,通过方差分析检验后,发现有差异。

要证明差异性比较的差异,就需要进行多重比较。

除试验设计之外,获得数据后,大量、重复的统计运算是我们在统计中要经常碰到的,而计算繁琐,计算精度不高又是统计工作的一大通病。

随着计算机的出现和发展,这一状况得到了很好的改善。

现代计算机软件技术的普及与发展促进了现代统计学的发展,多种专业统计分析软件的开发和应用,又极大方便了科技工作者的数据处理需要。

但是一些统计学专用软件(SA S 、S PSS 等),虽然功能强大,但对统计学专业背景知识要求较高,操作使用起来比较较困难。

而美国M ic rosoft 公司的通用办公软件中的电子表格除具备一般的数据管理外,还具有适合行业需要功能比较完善的数据分析工具。

用它进行科研数据的统计分析,易学易用、简明快捷;界面熟悉、结果直观。

是广大科研工作者进行科研数据的统计处理的一种高效工具。

体育多种教法之间的比较是体育科研、教研过程中要经常用到的。

所涉及的统计方法并不复杂,Exc e l 中内置了数据分析中就有单因素方差分析这一功能。

由于Exc e l 使用方法简便装机率高,如果用它来进行体育教法上的单因素方差分析,将会广大体育工作者在教法科研分析上提供极大的便利。

我们通过研究发现,使有Exc e l 中内置了数据分析工具,用V BA 扩展数据分析判断功能,可以完成数据的单国素方差分析和多重比较。

并且通过编程组合,能够简化界面,优化计算步骤,为我们体育数据统计分析提供一个准确、便利的工具平台。

2、Exc e l 中实现体育多种教法之间单因素方差分析的自动化()在x 中进行单因素方差分析的步骤第一步:首先进行单因素方差分析。

excel if 标准方差
在excel中，可以使用if函数和STDEV函数来计算标准方差。

首先，需要使用if函数筛选出符合特定条件的数据，并将这些数据作为参数传递给STDEV函数。

例如，如果要计算所有及格学生的标准方差，可以使用if函数筛选出成绩及格的数据，然后将这些数据作为参数传递给STDEV函数。

具体步骤如下：
1.在单元格中输入数据集。

假设数据集位于A1:A10单元格。

2.在B1单元格中输入条件，判断是否及格，例如“=A1>=60”。

这
个条件将返回TRUE或FALSE。

3.在C1单元格中使用IF函数来筛选数据。

函数公式如下：=IF(B1,
A1, "")。

这个函数的含义是，如果B1单元格为真（即成绩及格），则返回A1单元格的值，否则返回空值。

4.将C1单元格的公式拖到C2:C10单元格，以应用相同的条件。

5.在D1单元格中使用STDEV函数来计算标准方差。

函数公式如下：
=STDEV(C1:C10)。

《统计学》课程实验指导【试验目的】能够使学生在学习统计学原理课程时，掌握统计学中的计算过程，理论联系实际。

由于Excel是目前办公软件中比较流行的软件，因此，本试验课以该软件为基础，实现它的统计计算功能。

通过该试验课程的学习，使每个学生能够达到能够利用该软件的统计计算功能熟练地完成教材中有关例题、习题的计算，并通过案例的学习，培养学生一定的解决实际问题的能力。

【试验内容】Excel中的统计分析功能，包括算术平均数、加权平均数、方差、标准差、协方差、相关系数、统计图形、随机抽样、参数点估计、区间估计、假设检验、方差分析、移动平均、指数平滑、回归分析。

【试验计划】两个教学周，上试验课一次，时间一小时。

【试验地点】学院办公楼二层计算机机房试验一：描述性统计在Excel中的操作程序此分析工具用于生成对输入区域中数据的单变值分析，提供有关数据趋中性和易变性的信息。

（-）“描述统计”对话框输入区域在此输入待分析数据区域的单元格引用。

该引用必须由两个或两个以上按列或行组织的相邻数据区域组成。

分组方式如果需要指出输入区域中的数据是按行还是按列排列，请单击“逐行”或“逐列”。

标志位于第一行/列如果输入区域的第一行中包含标志项，请选中“标志位于第一行”复选框；如果输入区域的第一列中包含标志项，请选中“标志位于第一列”复选框；如果输入区域没有标志项，则该复选框不会被选中，Microsoft Excel 将在输出表中生成适宜的数据标志。

平均数置信度如果需要在输出表的某一行中包含均值的置信度，请选中此复选框，然后在右侧的编辑框中，输入所要使用的置信度。

例如，数值 95% 可用来计算在显著性水平为 5% 时的均值置信度。

第 K 大值如果需要在输出表的某一行中包含每个区域的数据的第 k 个最大值，请选中择此复选框，然后在右侧的编辑框中，输入 k 的数值。

如果输入 1，则这一行将包含数据集中的最大数值。

第 K 小值如果需要在输出表的某一行中包含每个区域的数据的第 k 个最小值，请选中此复选框，然后在右侧的编辑框中，输入 k 的数值。

Excel 数据管理与图表分析 双因素方差分析在实际问题的研究中，有时需要考虑两个因素对实验结果的影响。

例如饮料销售，除了关心饮料颜色之外，还需要了解销售地区的不同是否影响销售量。

若把饮料的颜色看作影响销售量的因素A ，饮料的销售地区则是影响因素B 。

对因素A 和因素B 同时进行分析，就属于双因素方差分析的内容。

双因素方差分析的类型主要有两种，下面具体介绍其应用。

1．无重复双因素分析无重复双因素分析是指在假设两个因素之间是相互独立、不存在任何关系的情况下，对其进行分析。

与单因素方差分析类似，在分析前需将试验数据按一定的格式输入工作表中。

例如，对A 、B 、C 和D 地区上半年和下半年的销售额进行统计，其数据信息如图13-6所示。

图13-6 创建表格 图13-7 设置无重复双因素参数单击【分析】组中的【数据分析】按钮，在弹出的【数据分析】对话框中，选择【方差分析：无重复双因素分析】选项。

然后，在【方差分析：无重复双因素分析】对话框中，设置相关的参数，如图13-7所示。

其中，在【方差分析：无重复双因素分析】对话框中，各选项功能如下： ●输入区域 输入无重复双因素分析的数据区域。

● 标志 启用该复选框，则生成的分析数据结果工作表中包含数据标志。

若禁用该复选框，则选择的分析数据中只能是数值类型，不能为文本类型，且生成的分析数据结果工作表中不包含数据标志。

●α 显著性水平，一般输入0.05，即95%的置信度。

● 输出选项 输出无重复双因素分析数据的结果。

提 示 【方差分析：无重复双因素分析】对话框中的参数与【方差分析：单因素方差分析】对话框中的参数相同。

单击【方差分析：无重复双因素分析】对话框中的【确定】按钮，即可得到如图13-8所示的方差分析结果。

创建表格 选择分析结果图13-8 无重复双因素方差分析在生成的Sheet4无重复双因素方差分析工作表中，分为上下两部分。

其中，上部分为4个地区及上、下半年的计数、求和、平均和方差。

Excel在方差分析中的应用摘要：方差分析是一种重要和常用的统计分析方法，使用常规方法进行方差分析是相当复杂的，而利用Excel 进行方差分析则可以轻松、快速地得出分析结果，使得我们可以把主要精力投入到实验设计和数据处理上，在教学时则可以腾出时间多讲授一些实验设计方面的内容而不必为复杂的计算伤脑筋。

关键词：方差分析；Excel;实验教学The application of Excel in variance analysisYin DezhongBeijing normal university, Beijing, 100875, ChinaAbstract: Anova is a kind of important and commonstatistical analysis method, and using a conventional methods for analysis of variance is very complicated, but using Excel can easily and quickly conclude the results of analysis, so than we can focus the experimental design and data collation and make more time for teaching the content of experimental design, not necessary to take the trouble doing the complex calculations.Key words: Anova; Excel; experimental teaching方差分析在推断统计分析中是很常用也很重要的一种统计分析方法，20 世纪20 年代由英国的统计学家R.A.Fisher首先提出，并以其姓的第一个字母F命名其统计量，故方差分析又称F 检验。

使用Excel进行数据建模与分析第一章：Excel的基础知识与数据导入1.1 Excel的介绍和重要性1.2 Excel的界面和基本功能1.3 如何导入和导出数据第二章：数据清洗与处理2.1 数据清洗的概念和重要性2.2 数据清洗的步骤和方法2.3 数据清洗实例：处理缺失值、异常值和重复值第三章：数据可视化与探索3.1 可视化的作用和重要性3.2 Excel中的常用图表类型及制作方法3.3 利用图表进行数据探索和分析的案例第四章：数据建模与分析4.1 数据建模的概念和步骤4.2 常用的数据建模方法和技巧4.3 Excel中的数据建模案例：线性回归模型、决策树模型等第五章：高级数据分析与统计5.1 数据分析的重要性和应用领域5.2 Excel中的高级数据分析工具及使用方法5.3 实例：利用Excel进行假设检验和方差分析第六章：数据报表与信息化分析6.1 数据报表的作用和要素6.2 制作数据报表的技巧和注意事项6.3 Excel中的数据报表案例：销售报表、财务报表等第七章：数据挖掘与预测分析7.1 数据挖掘的概念和重要性7.2 Excel中常用的数据挖掘工具和算法7.3 实例：利用Excel进行关联规则挖掘和时间序列预测分析第八章：数据模型的评估和改进8.1 数据模型评估的指标和方法8.2 Excel中的模型评估工具及使用技巧8.3 实例：利用Excel进行模型评估和改进结语：通过本文的介绍和讲解，我们了解了使用Excel进行数据建模与分析的基础知识和方法。

无论是数据清洗、数据可视化、数据建模，还是高级数据分析和预测分析，Excel都提供了丰富的功能和工具。

只要我们熟练掌握Excel的使用技巧，就能够轻松进行各种数据分析工作，为决策和问题解决提供支持。

希望本文对读者在Excel数据建模与分析方面有所帮助。

利用Excel的数据分析工具进行假设检验一、引言在当今数据驱动的世界中，数据分析被广泛应用于各个领域。

假设检验是数据分析中常用的统计方法之一，用于验证某个假设是否成立。

而Excel作为一款强大的电子表格软件，提供了丰富的数据分析工具，可以方便地进行假设检验。

本文将介绍如何利用Excel的数据分析工具进行假设检验，以帮助读者更好地理解和运用这一方法。

二、假设检验的概念假设检验是一种基于样本数据对总体参数假设进行判断的统计方法。

它分为单样本假设检验、双样本假设检验和方差分析等多种类型。

其中，单样本假设检验主要用于单个样本均值或比例的判断，而双样本假设检验则用于两个样本均值或比例的比较。

三、Excel的数据分析工具Excel提供了丰富的数据分析工具，可以方便地进行假设检验。

以下是其中几个常用的工具：1. 描述统计描述统计工具用于计算数据集的基本统计量，并绘制统计图表。

通过对数据的均值、标准差、最大最小值等进行分析，可以初步了解数据的分布情况。

2. t检验t检验是一种用于检验两个样本均值是否存在显著差异的方法。

在Excel中，可以通过"T.TEST"函数进行t检验的计算。

通过输入两个样本的数据范围和假设的均值差异，Excel将自动计算出t值、P值等结果，并判断两个样本均值是否存在显著差异。

3. 卡方检验卡方检验用于验证两个变量之间是否存在相关性。

在Excel中，可以通过"CHITEST"函数进行卡方检验的计算。

通过输入两个变量的数据范围，Excel将自动计算出卡方值、P值等结果，并判断两个变量之间是否存在相关性。

四、应用实例为了更好地理解和应用Excel的数据分析工具进行假设检验，以下是一个具体的应用实例：假设有两个班级的学生成绩数据，分别为班级A和班级B。

现在我们想要判断班级A和班级B的平均成绩是否存在显著差异。

我们可以按照以下步骤使用Excel进行假设检验：1. 收集数据首先，需要收集班级A和班级B的学生成绩数据，可以将数据分别输入到Excel的两个工作表中。

方差的应用实例方差是统计学中一种重要的描述数据分散程度的量度。

它在各个领域都有广泛的应用。

下面就来介绍一些方差的应用实例。

首先，在金融领域，方差被广泛应用于风险管理。

投资者在进行资产配置时，需要考虑不同投资组合的风险水平。

方差可以帮助投资者计算不同投资组合的风险程度，从而做出更明智的投资决策。

通过比较不同投资组合的方差，投资者可以选择风险适中的投资组合，以平衡收益和风险。

其次，在工程领域，方差被广泛用于质量控制。

在生产过程中，产品的质量往往会存在一定的波动。

方差可以帮助工程师评估生产过程的稳定性和一致性。

通过监控方差的变化，工程师可以及时发现生产过程中的异常情况，并采取相应的措施进行调整，以提高产品的质量稳定性。

此外，在医学研究中，方差也有重要的应用。

例如，在临床试验中，为了评估一种新药物的疗效，研究人员需要比较治疗组和对照组的治疗效果。

方差可以帮助研究人员计算不同组别之间的差异，并判断这种差异是否具有统计学意义。

通过方差分析等统计方法，研究人员可以得出结论，从而为临床实践提供科学的依据。

最后，在市场调研中，方差也有广泛应用。

市场调研往往需要收集大量的数据，并对数据进行分析。

方差可以帮助研究人员了解不同样本之间的差异，从而更准确地评估市场情况。

通过方差分析和回归分析等统计方法，研究人员可以发现市场的规律和趋势，为企业的决策提供参考。

总而言之，方差作为一种重要的统计量，广泛应用于金融、工程、医学和市场调研等领域。

它帮助我们评估风险、控制质量、评估疗效以及了解市场情况。

方差的应用使得我们能够更准确地分析数据，做出更科学的决策，对于各行各业的发展起到了积极的推动作用。

如何使用Excel进行统计分析和建模第一章：Excel基础知识Excel作为一款数据处理软件，具有广泛的应用范围。

在开始进行统计分析和建模之前，我们首先需要掌握一些基础知识。

首先是Excel的基本操作，包括创建和保存工作簿、插入和删除工作表等。

其次是单元格的操作，如输入数据、格式化单元格、使用函数等。

还有图表的制作和美化、筛选和排序数据等功能。

第二章：数据准备与清洗在进行统计分析和建模之前，我们需要对数据进行准备与清洗。

首先，确定数据的来源和目标，将需要的数据导入到Excel中。

然后，对数据进行筛选和排序，找出需要分析的部分。

接下来，需要对数据进行清洗和转换。

这包括处理缺失数据、异常值和重复数据。

我们还可以使用Excel的文本函数和数值函数对数据进行清洗和转换。

第三章：数据可视化与描述统计数据可视化是一种直观展示数据的方式。

在Excel中，我们可以使用图表功能进行数据的可视化。

根据数据的类型，选择合适的图表类型。

例如，使用柱状图和折线图展示数据的分布和趋势，使用饼图展示不同类别的占比。

除了图表，我们还可以使用Excel的条件格式和数据透视表来对数据进行可视化。

条件格式可以通过背景色和字体颜色等方式来突出显示特定的数据。

数据透视表可以对大量数据进行汇总和分析。

此外，描述统计是对数据进行总结和概括的方法。

我们可以使用Excel的统计函数，如平均值、中位数、标准差等来描述数据的特征。

另外，使用Excel提供的数据分析工具，如频率分布分析、相关性分析等，可以得到更加详细的数据描述。

第四章：假设检验与回归分析假设检验是一种判断统计推断是否成立的方法。

在Excel中，我们可以使用t检验和方差分析来进行假设检验。

通过计算得到的P值，可以判断两个样本之间的差异是否显著。

而回归分析是一种建立数学模型来解释变量之间关系的方法。

在Excel中，我们可以使用回归分析工具来进行回归分析。

通过选择适当的自变量，建立回归模型，并对模型进行评估和解释。

用excel求标准差在统计学中，标准差是一种衡量数据分散程度的重要指标。

在实际工作和生活中，我们经常需要用到Excel来进行数据处理和分析，因此掌握如何在Excel中求标准差是非常实用的技能。

本文将详细介绍如何使用Excel来求取标准差，并且通过实例演示来帮助读者更好地理解和掌握这一方法。

首先，让我们来了解一下标准差的概念。

标准差是一组数据的离散程度的度量，它衡量的是每个数据点相对于平均值的偏离程度。

标准差越大，说明数据点越分散；标准差越小，说明数据点越集中。

在Excel中，我们可以使用STDEV函数来求取一组数据的标准差。

接下来，我们将通过一个实例来演示如何在Excel中使用STDEV函数来求取标准差。

假设我们有一组数据，分别为10、15、20、25、30。

我们要求这组数据的标准差。

首先，我们需要在Excel中输入这组数据，然后在另一个单元格中输入STDEV函数，将这组数据作为函数的参数，按下回车键，即可得到这组数据的标准差。

除了使用STDEV函数外，Excel还提供了STDEVP函数和STDEV.S函数来分别求取总体标准差和样本标准差。

STDEVP函数适用于整个总体数据，而STDEV.S函数适用于样本数据。

在实际应用中，我们需要根据具体情况选择合适的函数来求取标准差。

除了单个数据集的标准差求取外，Excel还提供了多组数据的标准差求取功能。

我们可以使用数据分析工具中的方差分析功能来对多组数据的标准差进行比较和分析。

通过这一功能，我们可以更全面地了解不同数据集之间的差异和特点。

在使用Excel求取标准差时，我们还需要注意一些常见的错误和注意事项。

例如，如果数据中包含空白单元格或非数值类型的数据，就会导致标准差的计算出现错误。

因此，在进行标准差计算之前，我们需要对数据进行清洗和处理，确保数据的完整性和准确性。

总之，Excel是一个强大的数据处理和分析工具，通过掌握其中的标准差求取方法，我们可以更好地进行数据分析和决策。