普通年金终值、现值及年金的计算(有图解)
- 格式:ppt
- 大小:795.50 KB
- 文档页数:23



附表一 复利终值系数表计算公式:复利终值系数=()n i 1+,S=P ()ni 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和附表一 复利终值系数表 续表注:*〉99 999计算公式:复利终值系数=()n i 1+,S=P ()ni 1+P —现值或初始值 i —报酬率或利率 n —计息期数 S —终值或本利和附表二 复利现值系数表注:计算公式:复利现值系数=()-ni 1+,P=()ni 1S+=S ()-ni 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和附表二 复利现值系数表 续表注:*<0.0001计算公式:复利现值系数=()-ni 1+,P=()ni 1S+=S ()-ni 1+P —现值或初始值;i —报酬率或利率;n —计息期数;S —终值或本利和附表三年金终值系数表注:计算公式:年金终值系数=()i1i1n-+,S=A()i1i1n-+A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;S—年金终值或本利和附表三年金终值系数表续表注:*>999 999.99计算公式:年金终值系数=()i1i1n-+,S=A()i1i1n-+A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;S—年金终值或本利和附表四年金现值系数表计算公式:年金现值系数=()ii11n-+-,P=A()ii11n-+-A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;P—年金现值或本利和附表四年金现值系数表续表注:计算公式:年金现值系数=()ii11n-+-,P=A()ii11n-+-A—每期等额支付(或收入)的金额;i—报酬率或利率;n—计息期数;P—年金现值或本利和。


各种年金的计算公式梳理及推导过程年金是指在一定期限内,等额、定期的系列收支。
在财务和经济领域,年金有着广泛的应用,不同类型的年金,其计算公式和推导过程也有所不同。
接下来,咱们就一起梳理梳理各种年金的计算公式,并看看它们是怎么推导出来的。
先来说说普通年金。
普通年金就是从第一期期末开始,每期期末等额收付的年金。
比如说,咱们每个月月底发工资,这就可以近似看作是一个普通年金。
普通年金的终值计算公式是:F = A×[(1 + i)^n - 1]/i 。
这里的 F 表示年金终值,A 表示年金数额,i 表示利率,n 表示期数。
咱们来推导一下这个公式。
假设每年年末存入 A 元,年利率为 i ,存了 n 年。
第一年的 A 元到第 n 年末的本利和是 A×(1 + i)^(n - 1) ;第二年的 A 元到第 n 年末的本利和是 A×(1 + i)^(n - 2) ;以此类推,第 n 年的 A 元到第 n 年末的本利和就是 A 元。
把这些加起来,就得到了普通年金终值的计算公式。
再看看普通年金现值的计算公式:P = A×[1 - (1 + i)^(-n)]/i 。
这个 P 表示年金现值。
推导过程是这样的:假设未来 n 年内每年年末有 A 元的现金流入,年利率为 i 。
第 1 年年末的 A 元折合到现在的价值是 A/(1 + i) ;第 2 年年末的 A 元折合到现在的价值是 A/(1 + i)^2 ;一直到第 n 年年末的A 元折合到现在的价值是 A/(1 + i)^n 。
把这些现值加起来,就得到了普通年金现值的计算公式。
接着说预付年金。
预付年金是在每期期初等额收付的年金。
比如说,年初交房租,这就是预付年金。
预付年金终值的计算公式是:F = A×[(1 + i)^n - 1]/i ×(1 + i) 。
推导的时候,咱们可以把预付年金看成是普通年金,先计算出在 n - 1 期末的普通年金终值,然后再乘以 (1 + i) ,就得到了预付年金的终值。

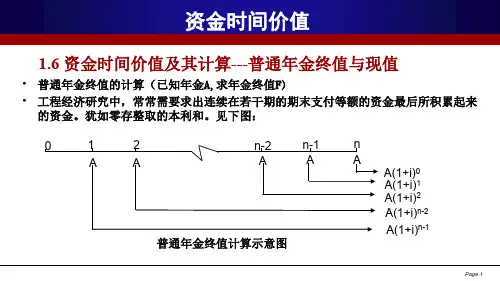
•普通年金终值的计算(已知年金A,求年金终值F)•工程经济研究中,常常需要求出连续在若干期的期末支付等额的资金最后所积累起来的资金。
犹如零存整取的本利和。
见下图:1.6 资金时间价值及其计算---普通年金终值与现值A(1+i)1 A(1+i)2 01 2 n-2 n-1 n AAAAAA(1+i)0 普通年金终值计算示意图A(1+i)n-2 A(1+i)n-1•由上图可知:年金终值的计算公式为:F=A(1+i)0+A(1+i)1+A(1+i)2+……+A(1+i)n-2+A(1+i)n-1…(1) 将(1)式两边同时乘上(1+i)得:F(1+i) = A(1+i)1+A(1+i)2+A(1+i)3 + ……+A(1+i)n-1+A(1+i)n …(2) 将(2)式减去(1)式得:F .i=A(1+i)n -A=A[(1+i)n -1]1.6资金时间价值及其计算---普通年金终值与现值(1+i)n-1[F= A ] …… (3) i1.6 资金时间价值及其计算---普通年金终值与现值(3)式中方括号中的数值,通常称作“年金终值系数”,记作(F/A,i,n)。
上式也可写作: F=A(F/A,i,n)[例3]假设某项目在5年建设期内每年年末向银行借款100万元,借款年利率为10%,问该项目竣工时应付本息的总额是多少?1.6 资金时间价值及其计算---普通年金终值与现值•年偿债基金的计算(已知年金终值F,求年金A)•年偿债基金的计算实际上是年金终值的逆运算。
其计算公式为:i ]A=F[(1+i)n-1上式也可写作:A=F(A/F,i,n)或:A=F[1/(F/A,i,n)]1.6 资金时间价值及其计算---普通年金终值与现值•年偿债基金的计算(已知年金终值F,求年金A)•[例4]:假设某企业有一笔4年后到期的借款,数额为1000万元,为此设置偿债基金,年复利率为10%,到期一次还清借款,问每年应存入的金额是多少?•普通年金现值的计算(已知年金A,求年金现值P)1.6 资金时间价值及其计算---普通年金终值与现值AAAA12 n-1 n P=A (1+i)-1+A (1+i)-2+A (1+i)-(n-1)+……..+A (1+i)-n =A[1-(1+i) –n / i]A (1+i)-1 A (1+i)-2A (1+i)-(n-1) A (1+i)-n假定这一系列收益会永远持续下去则有: P=A / i (永续年金)1.6 资金时间价值及其计算---普通年金终值与现值•上式中方括号内的数值称作“年金现值系数”,记作(P/A,i,n), •即:P=A(P/A,i,n)•[例5]租入某设备,每年年末需要支付租金120元,年复利率为10%,问5年内应支付的租金总额的现值是多少?1.6 资金时间价值及其计算---普通年金终值与现值•年资本回收额的计算(已知年金现值P,求年金A)•年金现值的逆运算,计算公式:A=P[i/1-(1+i)-n]•式中方括号内的数值称作“资本回收系数”记作(A/P,i,n)上式也可写作:•A=P (A/P,i,n)或A=P [1/(P/A,i,n)]•[例6]:某企业现在借得1000万元的贷款,在十年内以年利率12%均匀偿还,每年应付的金额是多少?。

年金终值与限制的计算范例1、普通年金现值和终值的计算1)普通年金的概念 P66普通年金,又称后付年金,是指每期期末有等额的收付款项的年金。
2)普通年金终值的计算 P66n,,(1,i),1普通年金终值(FVA),A(公式8),,i,,(1,i)n,1i被称为年金终值系数,用FVIFA表示 i,n则FVA=A×FVIFA公式8 i,n3) 普通年金现值的计算 P6811,,普通年金现值(PVA),A,(公式9)n,,ii(1,i),,11,被称为年金现值系数,用PVIFA表示i,nnii(1,i)则:PVA,A,PVIHA(公式9)i,n4)普通年金的应用例1:拟在5年后还清10000元债务,从现在起每年等额存入一笔款项,假如银行存款利率5%,问每年需要存入多少钱,解题思路:1)分析题目所给的资料,判断已知条件2)分析题目要求求解的问题3)选择适用公式进行计算或利用公式推导解: 解:已知年金终值FVA=10000,I=5%,n=5; 求年金A用公式8 n5 FVA=A[(1+i)-1]]/i=A[(1+5%)-1]/5%=10000A=1809.63或(查年金终值系数):FVA=A×FVIFA =A×5.526=10000 i,nA=1809.63例2:某人出国三年,请你代付房租,每年租金5000元,银行存款利率为5%,问他应当现在给你在银行存入多少钱,解:已知年金A=5000,n=3,I=5%;求年金现值PVA用公式9PVA=A×PVIFA=5000×2.7232=13615 ,in或:直接计算例3:某人在未来10年中,每年底存入3000元,他想拥有60912元,则年利率为多少,解:已知A=3000,n=10,FVA=60912;求利率IFVA=A×FVIFA=3000 ×FVIFA=60912 i,ni,nFVIFA=20.304 i,n查表可知当n=10,I=15%时,FVIFA=20.304 i,n所以 I=15%或: 用插入法计算。

造价年金计算公式一、普通年金终值计算公式。
1. 公式。
- 普通年金终值公式:F = A×((1 + i)^n-1)/(i),其中F为年金终值,A为年金(每年等额收付的金额),i为利率,n为计息期数。
- 例如,每年年末存入银行A = 1000元,年利率i=5%,存期n = 3年。
- 根据公式计算年金终值F = 1000×((1 + 0.05)^3 - 1)/(0.05)- 先计算(1 + 0.05)^3=1.05^3 = 1.157625,(1.157625-1)=0.157625,(0.157625)/(0.05)=3.1525,F = 1000×3.1525 = 3152.5元。
2. 推导过程(简单理解)- 普通年金终值是各期年金复利终值之和。
- 第1年年末的A元,到第n年年末的终值为A(1 + i)^n - 1;第2年年末的A 元,到第n年年末的终值为A(1 + i)^n - 2;以此类推,第n年年末的A元,终值就是A。
- 所以F=A(1 + i)^n - 1+A(1 + i)^n - 2+·s+A,这是一个等比数列求和,首项a_1 = A,公比q=(1 + i),项数n。
根据等比数列求和公式S_n=(a_1(q^n - 1))/(q - 1),这里q=(1 + i),a_1 = A,就得到F = A×((1 + i)^n-1)/(i)。
二、普通年金现值计算公式。
1. 公式。
- 普通年金现值公式:P = A×frac{1-(1 + i)^-n}{i},其中P为年金现值,A、i、n含义同前。
- 例如,每年年末收到A = 2000元,年利率i = 8%,共n = 5年。
- 计算年金现值P = 2000×frac{1-(1 + 0.08)^-5}{0.08}- 先计算(1 + 0.08)^-5≈0.680583,1 - 0.680583 = 0.319417,(0.319417)/(0.08)=3.9927125,P = 2000×3.9927125 = 7985.425元。

终值和现值公式
现值计算公式:P/A=1/i - 1/ [i(1+i)^n],(i表示报酬率,n表示期数,P表示现值,A表示年金)。
终值计算公式:(P/F,i,n)=(1+i)^(-n),(i表示报酬率,n表示期数,P表示现值,F表示年金)。
年金终值计算公式:F=A*(F/A,i,n)=A*(1+i)n-1/i,
其中(F/A,i,n)称作“年金终值系数”、可查普通年金终值系数表。
终值是现在的一笔钱或一系列支付款项按给定的利息率计算所得到的在某个未来时间点的价值。
终值和现值的计算公式区别
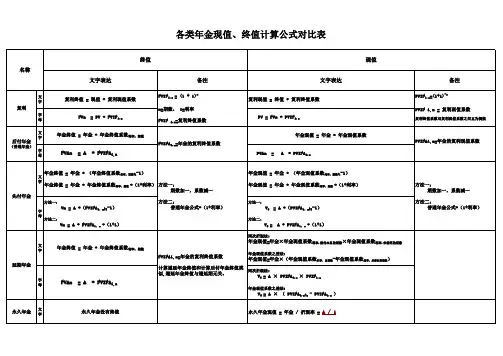
复利终值=P×(F/P,i,n),(F/P,i,n)为复利终值系数
复利现值=F×(P/F,i,n),(P/F,i,n)为复利现值系数
普通年金终值=A×(F/A,i,n),(F/A,i,n)为普通年金终值系数
普通年金现值=A×(P/A,i,n),(P/A,i,n)为普通年金现值系数
预付年金终值=A×(F/A,i,n)×(1+i)
预付年金现值=A×(P/A,i,n)×(1+i)
递延年金终值=A×(F/A,i,n)
递延年金现值=A×(P/A,i,n)×(P/F,i,m)=A×(P/A,i,m+n)-A×(P/A,i,m),递延期m(第一次有收支的前一期),连续收支期n
永续年金终值:没有
永续年金现值=A/i
终值是现在的一笔钱或一系列支付款项按给定的利息率计算所得到的在未来某个时间点的价值。
现值是未来的一笔钱或一系列支付款项按给定的利息率计算所得到的现在的价值。