轴承故障特征倍频公式推导
- 格式:docx
- 大小:90.43 KB
- 文档页数:4

深沟球轴承系列特征频率计算分析胡亮;董兆宇;戴煜林;程志学【摘要】Deep groove ball bearings are important parts of rotary machinery, which status directly affects the performance and lifespan of the rotary machines. In this paper, the natural frequencies of the components of SKF 60200 series deep groove ball bearings were calculated and the variation trend of the natural frequencies with the bearing size change was obtained. The fault characteristic frequencies of the components of the deep groove ball bearings were analyzed stochastically, and the fault probability distribution was obtained. With 6205-2RS JEM SKF deep groove ball bearings as the object, the characteristics of the vibration signal of the outer ring under normal condition and fault condition were analyzed respectively. The results have provided a guidance for fault analysis of bearings.%深沟球轴承作为旋转机械中的重要零件,其运行状态直接影响机器的性能和寿命。

144机械设计与制造Machinery Design&Manufacture第5期2021年5月结合频谱聚类与经验小波的轴承故障诊断方法唐泽娴1,林建辉1,张兵',杨基宏2(1.西南交通大学牵引动力国家重点实验室,四川成都610031;2.中车青岛四方机车车辆股份有限公司,山东青岛266111)摘要:实测轴承振动信号就有非平稳、非线性特征,因此,对该类信号的分析需要进行解调得到特征频率,在众多解调法中包络分析是最为常用的方法;为了使解调结果更加清晰,常在解调前进行滤波,达到滤除干扰成分可有效提升解调的效果。
经验小波变换提供了基于频带划分的小波滤波框架,划分后频带可滤除部分干扰信号,突出故障信号。
对此,受“箱型图”和层次聚类法的启发,对“突出值”聚类法进行频带划分,通过平方包络互相关系数选取合理的频带划分个数。
最后选取平方包络峭度值最大的滤波子信号进行Teager能量算子解调,获取特征频率。
文章针对不同工况下的不同故障类型轴承运行数据进行分析,验证算法的有效性。
特别地,在复合故障分析中,利用动态阈值法到达分别突出不同轴承故障频率的效果。
关键词:滚动轴承故障诊断;经验小波变换;箱型图;层次聚类;平方包络;动态阈值中图分类号:TH16;U270.3文献标识码:A文章编号:1001-3997(2021)05-0144-05Bearing Fault Diagnosis Method Using Spectral Clustering and Empirical WaveletTANG Ze-xian1,LIN Jian-hui1,ZHANG Bing1,YANG Ji-hong2(1.State Key Laboratory of Traction Power,Southwest Jiaotong University,Sichaun Chengdu610031,China;2.CRRC Qingdao Sifang Co.,Ltd.,Shandong Qingdao266111,China)Abstract:The measured bearing vibration signals are usually non-stationary and non-linear,so the demodulation is necessary to obtain the frequency characteristic frequency.A mong lots of demodulation methods,envelope analysis is the most popular one.When using the envelope analysis demodulation method,filtering is necessary to wipe out irrelevant signal components which can effectively improve the demodulation effect.Empirical wavelet transform provides a wavelet filter framework based on frequency band division and it can achieve the purpose of f iltering out the interfering signals and highlight fault signals.Inspired by box-plot andhierarchical clustering,the method of"outliers"clustering is proposed for frequency band division, and reasonable number of f requency band divis ion is selected by means of cross correlation coefficient.Finally,the filter signal with the maximum square envelope kurtosis value is selected for the square envelope demodulation to obtain the characteristic frequency employing the Teager energy operator.The validity of the algorithm is verified by analyzing the measured data of the failure bearingscf different kinds under different working conditions collected from a test bed.Specially, dynamic threshold is used to highlight the characteristic frequencies^different bearingfaults.Key Words:Rolling Bearing Fault Diagnosis;Empirical Wavelet Transform;Box Figure;Hierarchical Clustering;Squared Envelope;Dynamic Threshold1引言高速列车在交通与工业领域起到越来越重要的作用。

滚动轴承是一种常见的旋转机械零部件,它承担着重要的转动功能。
在滚动轴承工作过程中,如果遇到内外圈都旋转的故障,就需要对其特征频率进行计算和分析。
本文将介绍滚动轴承内外圈都旋转的故障特征频率计算公式,希望能够为相关领域的研究和实践提供帮助。
一、滚动轴承内外圈都旋转的故障特征频率计算公式1. 滚动轴承内外圈都旋转的故障特征频率公式如下:f = (P/2) * (1 - (d/D)) * (n/60)其中,f为故障特征频率,P为滚动体的数量,d为滚动体直径,D为滚动道直径,n为转速。
2. 在计算滚动轴承内外圈都旋转的故障特征频率时,需要注意以下几点:(1) 滚动体的数量对故障特征频率有影响,一般来说,滚动体数量越多,故障特征频率越高。
(2) 滚动体直径和滚动道直径的比值(d/D)也会影响故障特征频率,当d/D接近1时,故障特征频率较低;当d/D远离1时,故障特征频率较高。
(3) 转速的变化会直接影响到故障特征频率的计算,转速越高,故障特征频率越高。
二、滚动轴承内外圈都旋转的故障特征频率计算实例分析以某型号滚动轴承为例,其内外圈都旋转的故障特征频率计算如下:1. 已知数据:滚动体数量P=14,滚动体直径d=6mm,滚动道直径D=20mm,转速n=1800rpm。
2. 按照公式进行计算:f = (14/2) * (1 - (6/20)) * (1800/60) = 7 * 0.7 * 30 = 1470Hz。
通过以上实例分析可知,滚动轴承内外圈都旋转的故障特征频率为1470Hz。
这个特征频率对于故障诊断和预防具有重要意义,需要在相关实际应用中加以重视。
三、滚动轴承内外圈都旋转的故障特征频率计算公式的应用意义滚动轴承内外圈都旋转的故障特征频率计算公式的应用意义主要体现在以下几个方面:1. 故障诊断和预防:通过计算故障特征频率,可以帮助实现滚动轴承内外圈都旋转故障的诊断和预防工作,及早发现并解决故障问题,提高设备的可靠性和稳定性。

滚动轴承故障诊断初步1、故障原因滚动轴承的早期故障是滚子和滚道剥落、凹痕、破裂、腐蚀和杂物嵌入。
即主要故障形式:疲劳剥落、磨损、塑性变形、锈蚀、断裂、胶合、保持架损坏。
产生主要原因包括搬运粗心、安装不当、不对中、轴承倾斜、轴承选用不正确、润滑不足或密封失效、负载不合适以及制造缺陷。
2、频谱和波形特征滚动轴承它是由内圈、外圈、滚动体和保持架四部分组成。
当滚动体和滚道接触处遇到一个局部缺陷时,就有一个冲击信号产生。
缺陷在不同的元件上,接触点经过缺陷的频率是不相同的,这个频率就称为滚动轴承的特征频率。
滚动轴承的故障特征频率的数值一般在几赫兹到几百赫兹之间,在频谱图中的1000Hz以内的低频区域轴承故障特征频率如下:1、滚动轴承故障特征频率(外圈静止)式中:Z——滚动体个数fr——转频(Hz)D——轴承节径(mm)d——滚动体直径(mm)α——接触角(1)滚动轴承内圈故障特征频率(2)滚动轴承外圈故障特征频率(3)滚动轴承滚动体特征频率(4)滚动轴承保持架特征频率2、滚动轴承故障特征频率的计算经验公式:二、滚动轴承故障诊断的要素滚动轴承由内圈、外圈、滚动体和保持架四部分组成,每个轴承部件对应一个轴承故障特征频率。
滚动轴承的故障频率分布有一个明显的特点,往往在低频和高频两个频段内都有表现。
所以在频率分析时,可以选择在这两个频段进行分析。
根据滚动轴承的故障形式在频域中的表现形式,将整个频域分为三个频段,既高频段、中频段和低频段。
l 高频阶段指频率范围处于2000-5000Hz 的频段,主要是轴承固有频率,在轴承故障的早期,高频段反映比较敏感;中频阶段指频率范围处于800-1600Hz 的频段,一般是由于轴承润滑不良而引起碰磨产生的频率范围;l 低频阶段指频率范围处于0-800Hz 的频段,基本覆盖轴承故障特征频率及谐波;在高频段和低频段中所体现的频率是否为轴承故障频率,还要通过其他方法进行印证加以确认。
根据滚动轴承的故障特征频率在频域和时域中的表现,可将滚动轴承的诊断方法总结为三个频段;八个确认,简称三八诊断法。



滚动轴承故障诊断初步1、故障原因滚动轴承的早期故障是滚子和滚道剥落、凹痕、破裂、腐蚀和杂物嵌入。
即主要故障形式:疲劳剥落、磨损、塑性变形、锈蚀、断裂、胶合、保持架损坏。
产生主要原因包括搬运粗心、安装不当、不对中、轴承倾斜、轴承选用不正确、润滑不足或密封失效、负载不合适以及制造缺陷。
2、频谱和波形特征滚动轴承它是由内圈、外圈、滚动体和保持架四部分组成。
当滚动体和滚道接触处遇到一个局部缺陷时,就有一个冲击信号产生。
缺陷在不同的元件上,接触点经过缺陷的频率是不相同的,这个频率就称为滚动轴承的特征频率。
滚动轴承的故障特征频率的数值一般在几赫兹到几百赫兹之间,在频谱图中的1000Hz以内的低频区域轴承故障特征频率如下:1、滚动轴承故障特征频率(外圈静止)式中:Z——滚动体个数fr——转频(Hz)D——轴承节径(mm)d——滚动体直径(mm)α——接触角(1)滚动轴承内圈故障特征频率(2)滚动轴承外圈故障特征频率(3)滚动轴承滚动体特征频率(4)滚动轴承保持架特征频率2、滚动轴承故障特征频率的计算经验公式:二、滚动轴承故障诊断的要素滚动轴承由内圈、外圈、滚动体和保持架四部分组成,每个轴承部件对应一个轴承故障特征频率。
滚动轴承的故障频率分布有一个明显的特点,往往在低频和高频两个频段内都有表现。
所以在频率分析时,可以选择在这两个频段进行分析。
根据滚动轴承的故障形式在频域中的表现形式,将整个频域分为三个频段,既高频段、中频段和低频段。
l 高频阶段指频率范围处于2000-5000Hz 的频段,主要是轴承固有频率,在轴承故障的早期,高频段反映比较敏感;中频阶段指频率范围处于800-1600Hz 的频段,一般是由于轴承润滑不良而引起碰磨产生的频率范围;l 低频阶段指频率范围处于0-800Hz 的频段,基本覆盖轴承故障特征频率及谐波;在高频段和低频段中所体现的频率是否为轴承故障频率,还要通过其他方法进行印证加以确认。
根据滚动轴承的故障特征频率在频域和时域中的表现,可将滚动轴承的诊断方法总结为三个频段;八个确认,简称三八诊断法。
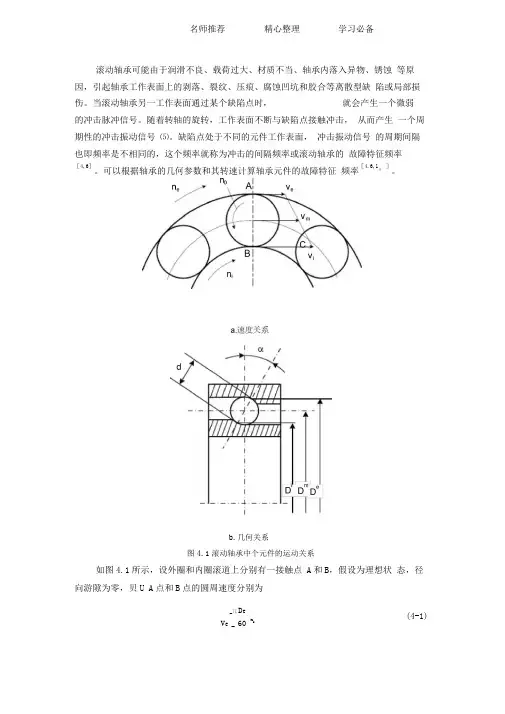
滚动轴承可能由于润滑不良、载荷过大、材质不当、轴承内落入异物、锈蚀等原因,引起轴承工作表面上的剥落、裂纹、压痕、腐蚀凹坑和胶合等离散型缺陷或局部损伤。
当滚动轴承另一工作表面通过某个缺陷点时,就会产生一个微弱的冲击脉冲信号。
随着转轴的旋转,工作表面不断与缺陷点接触冲击,从而产生一个周期性的冲击振动信号⑸。
缺陷点处于不同的元件工作表面,冲击振动信号的周期间隔也即频率是不相同的,这个频率就称为冲击的间隔频率或滚动轴承的故障特征频率[4,6]。
可以根据轴承的几何参数和其转速计算轴承元件的故障特征频率[4,6,1°]。
b.几何关系图4.1滚动轴承中个元件的运动关系如图4.1所示,设外圈和内圈滚道上分别有一接触点 A和B,假设为理想状态,径向游隙为零,贝U A点和B点的圆周速度分别为_兀D e(4-1)V e _ 60 n e兀D i V i=~60n iD i ——外圈、内圈滚道接触点处的直径,[mm ];外圈上某一点滚动体滚过频率为式中V e、 V i ――外圈、内圈滚道接触点处的圆周速度,[mm/s ]; n e、ni -- 外圈、内圈的转速, [r/mi n]。
dY =——cos aD m(4-3)式中 d ---- 滚动体直径,[mm ]; D m ——滚动体中心圆直径,[mm ];a ——接触角,指接触面中心与滚动体中心连线和轴承径向平面之 [弧度或角度]0间的夹角, 由图4-1 (b)可见 D e =D m +dcosa = D m (1 +Y ) D i =D m -dco<s = D m (1-Y )滚动体围绕轴承中心线的 公转线速度乃是V i 和V e 的平均值,即 V + V 八V m===^D m [n i (1"n e (1F滚动体的公转线速度也就是保持架中心圆的线速度。
保持架中心圆上某一点的线 速度为 沢D m Vm = —n m由上两式得保持架的转速为 (4-4) 内圈相对于保持架的转速为 F -nmni - ne [1 + Y ) 2 假设保持架上有z 个滚动体,内圈上某一点滚动体滚过频率为 N i =(n i -n m )z = 1(n i - n e 11 + Y k 2 n m (4-5)外圈相对于保持架的转速为 n em »n mV n dO(4-6)(4-2)D e 、N e = (n e — n m)Z = 2 (H e —)(1 ―丫滚动体的自转转速n o可由接触点处两物体线速度相等的关系求得。

SKF轴承异常振动频率的计算方法
我们在使用SKF轴承的时候,一定会遇到过轴承出现异常的时候,因为再好的轴承也不可能是无间断的正常运转,因为都会有个以外的情况发生,或者是因为设备问题,或者是因为SKF轴承本身,这些情况都是有可能发生的,所以我们只有事先准备好,有所了解,才能在故障发生的时候,能够应对自如,很好的解决出现的问题。
今天我们主要就是说一下SKF 轴承异常振动频率的计算方法,具体情况请看下面的公式和数据对应表:
SKF轴承外环故障频率:BPFOe≌N(0.5n-1.2)
轴承内环故障频率:BPFIe≌N(0.5n+1.2)
轴承滚动体故障频率:BSFe≌N(0.2n-1.2/n)
轴承保持架故障频率:FTFe≌N(0.5-1.2/n)
以上符号:
n=滚动体数目。
N=轴的转速。
注:1.滚动SKF轴承没有滑动;2.滚动轴承几何尺寸没有变化;3.轴承外环固定不旋转. SKF轴承外环故障频率:BPFOr≌0.4Nn
轴承内环故障频率:BPFIr≌0.6Nn
轴承保持架故障频率:FTFr≌0.4N
以上符号:
n=滚动体数目。
N=轴的转速。
注:1.滚动SKF轴承没有滑动;2.滚动轴承几何尺寸没有变化;3.轴承外环固定不旋转.。
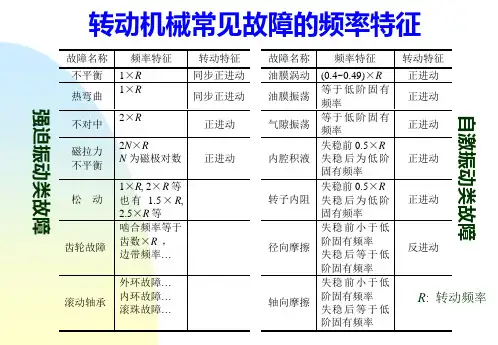

轴承故障特征倍频公式
推导
Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】
滚动轴承可能由于润滑不良、载荷过大、材质不当、轴承内落入异物、锈蚀等原因,引起轴承工作表面上的剥落、裂纹、压痕、腐蚀凹坑和胶合等离散型缺陷或局部损伤。
当滚动轴承另一工作表面通过某个缺陷点时,就会产生一个微弱的冲击脉冲信号。
随着转轴的旋转,工作表面不断与缺陷点接触冲击,从而产生一个周期性的冲击振动信号[5]。
缺陷点处于不同的元件工作表面,冲击振动信号的周期间隔也即频率是不相同的,这个频率就称为冲击的间隔频率或滚动轴承的故障特征频率[4,6]。
可以根据轴承的几何参数和其转速计算轴承元件的故障特征频率[4,6,10]。
a.速度关系
b.几何关系
图 滚动轴承中个元件的运动关系
如图所示,设外圈和内圈滚道上分别有一接触点A 和B ,假设为理想状态,径向游隙为零,则A 点和B 点的圆周速度分别为
e e
e n D v 60π= (4-1)
i i
i n D v 60π= (4-2)
式中 e v 、i v ——外圈、内圈滚道接触点处的圆周速度,[mm/s];
e D 、i D ——外圈、内圈滚道接触点处的直径,[mm];
e n 、i n ——外圈、内圈的转速,[r/min]。
令 αγcos m
D d = (4-3) 式中 d ——滚动体直径,[mm];
m D ——滚动体中心圆直径,[mm];
α——接触角,指接触面中心与滚动体中心连线和轴承径向平面之间的夹角,[弧度或角度]。
由图4-1(b )可见
e D =)1(cos γα+=+m m D d D
滚动体围绕轴承中心线的公转线速度乃是i v 和e v 的平均值,即
滚动体的公转线速度也就是保持架中心圆的线速度。
保持架中心圆上某一点的线速度为
由上两式得保持架的转速为 )]1()1([2
1γγ++-=e i m n n n (4-4) 内圈相对于保持架的转速为 ()()γ+-=-=12
1e i m i im n n n n n (4-5) 假设保持架上有z 个滚动体,内圈上某一点滚动体滚过频率为
外圈相对于保持架的转速为 ()()γ--=-=12
1i e m e em n n n n n (4-6) 外圈上某一点滚动体滚过频率为
滚动体的自转转速0n 可由接触点处两物体线速度相等的关系求得。
例如,滚动体与内圈接触的B 点相对于滚动体中心的线速度为
式中 0n 为滚动体自转转速。
内圈滚道上与滚动体接触着的B 点相对于滚动体中心的线速度为
根据纯滚动条件,滚动体上接触点B 和内圈滚道上相应的B 点速度相等,得到
由此可得滚动体的自转转速为 )1)((2)(20γ--=-=e i m m i i n n d
D n n d D n (4-7) 假如内圈滚道、外圈滚道或滚动体上有一处缺陷(剥落或裂纹等局部缺陷),则两种金属体在缺陷处相接触就会发生冲击作用,冲击的间隔频率见表4-1。
绝大多数滚动轴承在实际应用中总是保持外圈静止,内圈与轴一起旋转,当轴的转速为n 时,则有
由上面式(4-5)可得内圈相对于保持架的转速
因为保持架上有z 个滚动体,所以内圈上某一点每分钟通过的滚动体数为
z D d n z n N m
im i )cos 1(21α+== (4-8) 保持架相对于外圈的转速
[6]
外圈上某一点每分钟通过的滚动体数为
z D d n z n N m
em e )cos 1(21α-== (4-9) 滚动体自转速度为
)cos 1(2)1(2222
20αγm
m m D d n d D n d D n -=-= (4-10) 假如内圈滚道、外圈滚道或滚动体上有一处缺陷(剥落或裂纹等局部缺陷),则两种金属体在缺陷处相接触就会发生冲击作用,冲击的间隔频率见表4-2。