当前位置：文档之家 › 材料力学典型例题及解析 12.冲击问题典型习题解析

材料力学典型例题及解析 12.冲击问题典型习题解析

  • 格式：pdf
  • 大小：343.61 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

南京工业大学材料力学材料力学冲击问题

南京工业大学材料力学材料力学冲击问题

2. 计算轴AB横截面上的最大切应力
任一横截面上的扭矩为：
TTd
MMdd
00..55ππ((kkNNmm)) 33
轴横截面上的最大扭转切应力为：
dmmaaxxWWTPdt
00..55ππ 110033NNmm 33
ππ 110000110033mm 33
22..6699110066PPaa 22..6699MMPPaa
总伸长。
解：⒈ 求杆内最大动应力
向心加速度为 an 2 x
到轴线距离为x处杆单位长度上的动载荷为
qd
(x)
A
g
2
x
因此，距轴线距离为x的截面上的轴力为
FNd
l
x qd (x)dx
l A 2 xdx A 2 (l 2 x2 )
xg
2g
FNd
A 2
2g
(l 2
x2)
相应的动应力为
d (x)
P
速度开始下降至0，同时弹簧变形达到最
h
P
大值 d 。
P
d
此时，全部（动）势能转化为应变能， 杆内动应力达最大值（以后要回跳）。就
以此时来计算：
•释放出的动能（以势能的降低来表示）
弹簧
T P(h d )
•增加的应变能，在弹性极限内
Ve
1 2
Pdd
根据力和变形之间的关系：Fd kd
F
Fd
Fd ：冲击物速度为0时，作用于杆之力。
d Kd st
通常情况下，Kd 1 。
•关于动荷系数 K d 的讨论:
1.若冲击物是以一垂直速度v 作用于构件上，则由 v2 2gh
可得：
v2
Kd 1

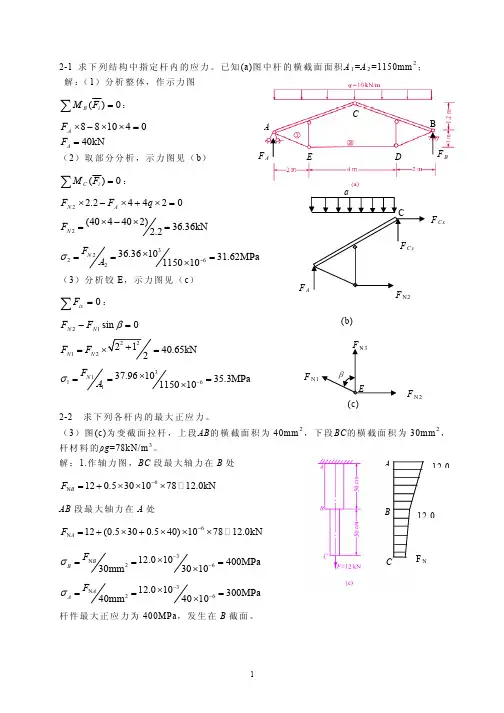
工程力学材料力学部分课后习题详解

工程力学材料力学部分课后习题详解

2-1 求下列结构中指定杆内的应力。

已知(a)图中杆的横截面面积A 1=A 2=1150mm 2； 解：（1）分析整体，作示力图∑=0)(i BF M：CB 041088=××−×A F AF N1F N2(c)40kN A F =（2）取部分分析，示力图见（b ）∑=0)(i CF M：02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×（3）分析铰E ，示力图见（c ）∑=0ix F ：0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。

（3）图(c)为变截面拉杆，上段AB 的横截面积为40mm 2，下段BC 的横截面积为30mm 2，杆材料的ρg =78kN/m 3。

解：1.作轴力图，BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ，发生在B 截面。

EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ，标距为200mm 的合金钢杆，比例极限内进行拉伸试验，当轴向荷载从零缓慢地增加58.4kN 时，杆伸长了0.9mm ，直径缩小了0.022mm ，确定材料的弹性模量E 、泊松比µ。

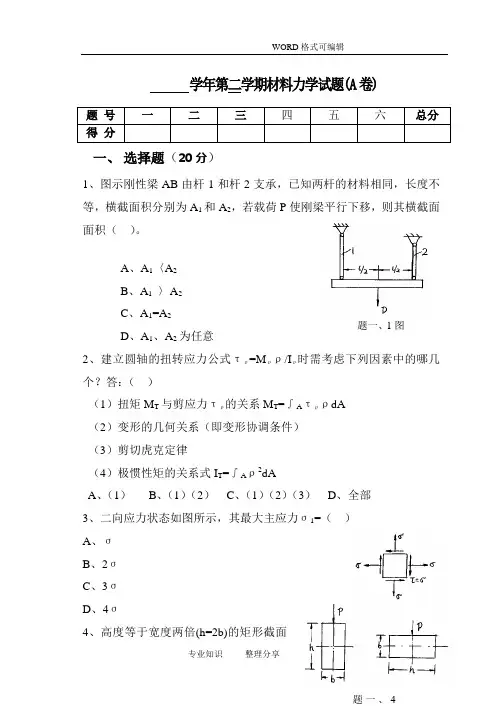
材料力学的练习试题和的答案解析_全

材料力学的练习试题和的答案解析_全

学年第二学期材料力学试题(A 卷)一、 选择题（20分）1、图示刚性梁AB 由杆1和杆2支承，已知两杆的材料相同，长度不等，横截面积分别为A 1和A 2，若载荷P 使刚梁平行下移，则其横截面面积（ ）。

A 、A 1〈A 2B 、A 1 〉A 2C 、A 1=A 2D 、A 1、A 2为任意2、建立圆轴的扭转应力公式τρ=M ρρ/I ρ时需考虑下列因素中的哪几个？答：（ ）（1）扭矩M T 与剪应力τρ的关系M T =∫A τρρdA （2）变形的几何关系（即变形协调条件） （3）剪切虎克定律（4）极惯性矩的关系式I T =∫A ρ2dAA 、（1）B 、（1）（2）C 、（1）（2）（3）D 、全部 3、二向应力状态如图所示，其最大主应力σ1=（ ） A 、σ B 、2σ C 、3σ D 、4σ4、高度等于宽度两倍(h=2b)的矩形截面题 号 一 二 三 四 五 六 总分 得 分题一、3图题一、1图梁，承受垂直方向的载荷，若仅将竖放截面改为平放截面，其它条件都不变，则梁的强度（）A、提高到原来的2倍B、提高到原来的4倍C、降低到原来的1/2倍D、降低到原来的1/4倍5. 已知图示二梁的抗弯截面刚度EI相同，若二者自由端的挠度相等，则P1/P2=（）A、2B、4C、8题一、5图D、16二、作图示梁的剪力图、弯矩图。

（１５分）二题图三、如图所示直径为d的圆截面轴，其两端承受扭转力偶矩m的作用。

设由实验测的轴表面上与轴线成450方向的正应变，试求力偶矩m之值、材料的弹性常数E、μ均为已知。

（15分）三题图四、电动机功率为9kW ，转速为715r/min ，皮带轮直径D =250mm ，主轴外伸部分长度为l =120mm ，主轴直径d =40mm ，〔σ〕=60MPa ，用第三强度理论校核轴的强度。

（15分）五、重量为Q 的重物自由下落在图示刚架C 点，设刚架的抗弯刚度为EI ，试求冲击时刚架D 处的垂直位移。

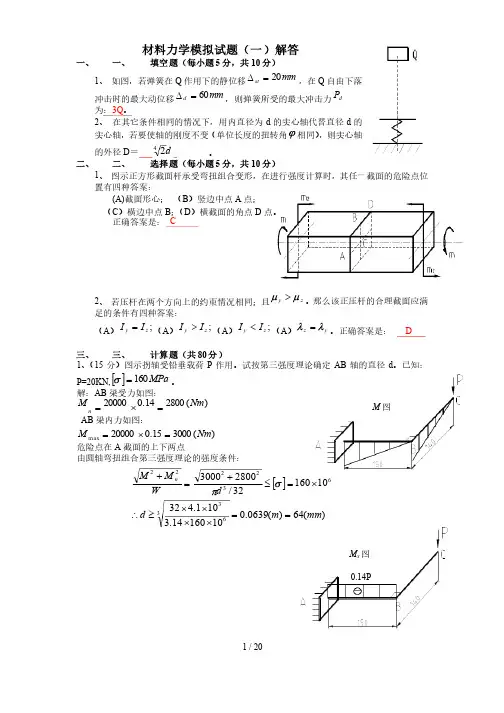
材料力学试题带参考答案解析

材料力学试题带参考答案解析

1 / 20材料力学模拟试题（一）解答一、 一、 填空题（每小题5分，共10分）1、 如图，若弹簧在Q 作用下的静位移mm st 20=D ，在Q 自由下落冲击时的最大动位移mm d 60=D ，则弹簧所受的最大冲击力d P 为：3Q 。

2、 在其它条件相同的情况下，用内直径为d 的实心轴代替直径d 的实心轴，若要使轴的刚度不变（单位长度的扭转角j 相同），则实心轴的外径D ＝ d 42 。

二、 二、 选择题（每小题5分，共10分）1、 图示正方形截面杆承受弯扭组合变形，图示正方形截面杆承受弯扭组合变形，在进行强度计算时，在进行强度计算时，其任一截面的危险点位置有四种答案：置有四种答案：(A)截面形心；截面形心； （B ）竖边中点A 点；点；（C ）横边中点B ；（D ）横截面的角点D 点。

点。

正确答案是：正确答案是：C2、 若压杆在两个方向上的约束情况相同；若压杆在两个方向上的约束情况相同；且且z y m m >。

那么该正压杆的合理截面应满足的条件有四种答案：足的条件有四种答案：（A ）;z y I I =（A ）;z y I I >（A ）;z y I I <（A ）y z l l =。

正确答案是：。

正确答案是： D三、 三、 计算题（共80分） 1、（15分）图示拐轴受铅垂载荷P 作用。

试按第三强度理论确定AB 轴的直径d 。

已知：P=20KN,[]MPa 160=s 。

解：AB 梁受力如图：梁受力如图： )(280014.020000Nm M n =´= AB 梁内力如图：梁内力如图：)(300015.020000max Nm M =´=危险点在A 截面的上下两点截面的上下两点由圆轴弯扭组合第三强度理论的强度条件：由圆轴弯扭组合第三强度理论的强度条件：[])(64)(0639.01016014.3101.4321016032/28003000363632222mm m d d W M M n ==´´´´³\´=£+=+s pM 图0.14PM x 图2、图示矩形截面钢梁，A 端是固定铰支座，B 端为弹簧支承。

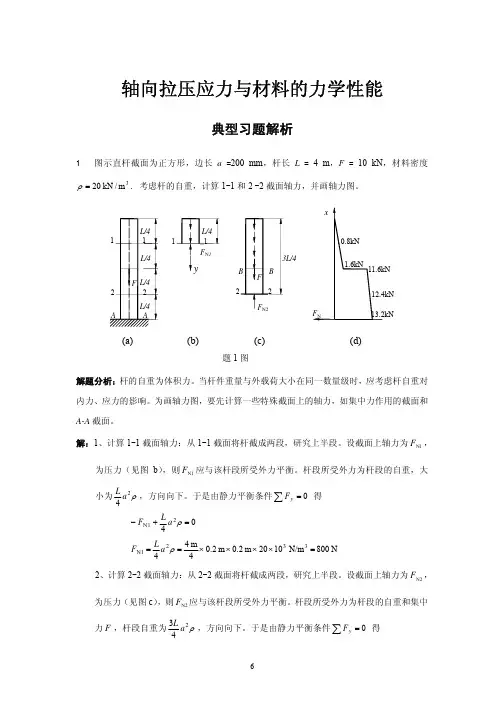
材料力学典型例题与详解(经典题目)

材料力学典型例题与详解(经典题目)
G = [σ ]A(l) − F
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18，或 1.33∶1.09∶1。 讨论：计算结果表明，采用等强度石柱时最节省材料，这是因为这种设计使得各截面的正应 力均达到许用应力，使材料得到充分利用。 3 滑轮结构如图，AB 杆为钢材，截面为圆形，直径 d = 20 mm ，许用应力 [σ ] = 160 MPa ，BC 杆为木材，截面为方形，边长 a = 60 mm ，许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解：1、计算 1-1 截面轴力：从 1-1 截面将杆截成两段，研究上半段。设截面上轴力为 FN1 ，
为压力（见图 b），则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重，大

材料力学习题及答案

材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆，两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。

试问在杆件的任一横截面m-m上存在何种内力分量，并确定其大小。

解：从横截面m-m将杆切开，横截面上存在沿轴线的内力偶矩分量M x，即扭矩，其大小等于M。

1-2 如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。

解：应力p与斜截面m-m的法线的夹角α=10°，故σ＝p cosα=120×cos10°=118.2MPaτ＝p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆，横截面上的正应力沿截面高度线性分布，截面顶边各点处的正应力均为σmax=100 MPa，底边各点处的正应力均为零。

试问杆件横截面上存在何种内力分量，并确定其大小。

图中之C点为截面形心。

解：将横截面上的正应力向截面形心C简化，得一合力和一合力偶，其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。

试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。

解：第二章轴向拉压应力2-1试计算图示各杆的轴力，并指出其最大值。

解：(a) F N AB=F, F N BC=0, F N，max=F(b) F N AB=F, F N BC=－F, F N，max=F(c) F N AB=－2 kN, F N2BC=1 kN, F N CD=3 kN, F N，max=3 kN(d) F N AB=1 kN, F N BC=－1 kN, F N，max=1 kN2-2 图示阶梯形截面杆AC，承受轴向载荷F1=200 kN与F2=100 kN，AB段的直径d1=40 mm。

冲击问题典型习题解析

冲击问题典型习题解析
所以本问题的动载荷因数为： k d =
∆d 2h 2 × 440 × 10 −3 m = 1+ 1+ = 1+ 1+ = 22 ∆st ∆st 2 × 10 −3 m
讨论： （1） 、在线弹性范围内，载荷、变形、应变、应力之间都是线性关系，也就是说，当 外载荷被放大 k d 倍，则变形、应力、应变也同样被放大 k d 倍。所以有 σ d = k dσ st 。有了 k d 很 方便就能计算出动载荷条件下被冲击物的各量。 （2） 、但应注意，对不同的问题， k d 有不同 的表达式，不能生搬硬套。 （3 ） 、掌握本题所采用的以能量守恒为基本原理的分析方法是最 重要的。 3 一个橡胶小球重 W = 300 mN ，用一橡皮筋连在一木拍上，橡皮筋长 L0＝300 mm ，横截 面面积 A = 1.6 mm 2 ，弹性模量 E = 2.0 MPa 。用木拍击打小球后，小球拉动橡皮筋，使橡 皮筋总长达到 L1 = 1.0 m ，试问小球离开木拍瞬间的速度是多少？假设橡皮筋为线弹性体， 而且忽略小球的势能。 解题分析：木拍击打小球是冲击载荷问题。小球受木拍撞击飞出，将连接小球和木拍的橡皮 筋拉长。小球离开木拍的瞬间有一个初速度，橡皮筋被拉长的同时，小球速度不断减小，当 小球速度为零时，橡皮筋被拉至最长。假设不考虑小球的势能变化，则小球离开木拍瞬间的 动能完全转化为橡皮筋的应变能。即 E k = Vε 。 解：设小球离开木拍瞬间速度为 υ ，则其动能 E k =
0.8 m 1.944 × 10 2 m ) = 3.963 × 10 −3 m
∆d = 1.944 × 10 −5 m(1 + 1 +
考虑到 Fd =
EA ⋅ ∆d ，所以绳中最大应力 b
σd =

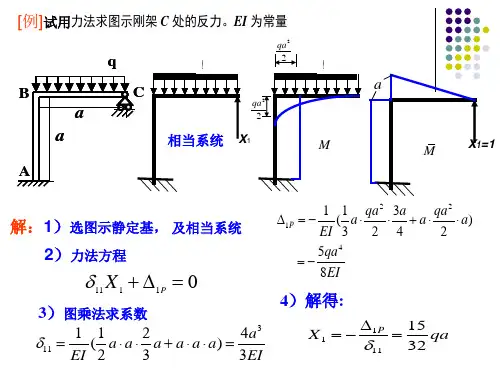
材料力学力法典型例题解

材料力学力法典型例题解

l
q
RB
B
l q
X1
B Δ1F
B δ11
1
Example 2 .画图示钢架旳弯矩图，EI=const .
P
a
B
A
CP B
A
a
CP
a
B
C
B
C
X1
M
1
M
A
A
Pa
a
解 : 1）选图示相当系统（：一次超静定）
2）力法方程：
X 0
11 1
1P
3）利用图乘法求系数:
a
P
a
B
A
a
C
P
a
B
C
B
C
M
1
M
A
A
PPal
X1
2）力法方程
F
X 0
11 1
1P
3）图乘法求系数
11
2 EI
(1 2
aa
2 3
a)
2a3 3EI
1P
2 EI
(1 2
a
Fa
2 3
a)
a a
2Fa3
M
3EI
4）解得:
1
C
X1
1P
11
F
1
C
Fa
X1=1 Fa
F
1
M
F
F1 C
F
Example 1 . 求RB (EI=const.).
解: 1）选图示相当系统 （一次超静定）
B
CP
P
P
a
a
X1
a a
X1 1
A
Pa
解：1）选图示静定基及相当系统

材料力学内部习题集及问题详解

材料力学内部习题集及问题详解

第二章轴向拉伸和压缩2-1 一圆截面直杆，其直径d ＝20mm, 长L =40m ，材料的弹性模量E =200GPa ，容重γ＝80kN/m 3, 杆的上端固定，下端作用有拉力F =4KN ，试求此杆的：⑴最大正应力； ⑵最大线应变； ⑶最大切应力；⑷下端处横截面的位移∆。

题 2 - 1 图+5004.8N4000N解：首先作直杆的轴力图⑴最大的轴向拉力为232N,max 80100.024*********.8N 44d F V F L F ππγγ=+=+=⨯⨯⨯⨯+= 】故最大正应力为：N,maxN,maxN,maxmax 222445004.8=15.94MPa 3.140.024F F F Ad d σππ⨯====⨯⑵最大线应变为:64maxmax915.94100.7971020010E σε-⨯===⨯⨯ ⑶当α（α为杆内斜截面与横截面的夹角）为45︒时，maxmax 7.97MPa 2ασττ===⑷取A 点为x 轴起点，2N (25.124000)N 4d F Vx F x F x πγγ=+=+=+故下端处横截面的位移为：240N 0025.1240001d d (12.564000)2.87mm LL F x x x x x EA EA EA+∆===⋅+=⎰⎰2-2 试求垂直悬挂且仅受自重作用的等截面直杆的总伸长△L 。

已知杆横截面面积为A ，长度为L ,材料的容重为γ。

AB题 2-2 图A B解：距离A 为x 处的轴力为N ()F x Ax γ=⋅ 所以总伸长 2N 00()L d d 2LL F x Ax L x x EA EA Eγγ∆===⎰⎰ 【2-3 图示结构，已知两杆的横截面面积均为A =200mm 2,材料的弹性模量E =200GPa 。

在结点A 处受荷载F 作用，今通过试验测得两杆的纵向线应变分别为ε1＝4×10－4，ε2＝2×10－4，试确定荷载P 及其方位角θ的大小。

材料力学全部习题解答讲解

材料力学全部习题解答讲解

1 2 R2
3
2
（b）
yc =
ydA
A
=
A
b 0
y ayndy b ayndy
=
n n

1 2
b
0
26
Iz =
y2dA
A
Iy =
z2dA
A
解： 边长为a的正方截面可视为由图示截面和一个半 径为R的圆截面组成，则
Iz
=I（za）
I（zR）=
a4 12


2R 4
0

FN A
10103 N 1000 106 m2
10MPa
由于斜截面的方位角 450
得该截面上的正应力和切应力分别为
45
0 cos2 10106 cos2 450 pa 5MPa
0 sin 2 1 10106 sin 900 pa 5MPa
2
18
解：1.求预紧力 由公式l FNl 和叠加原理，故有
EA
l

l1

l2

l3

Fl1 EA1

Fl2 EA2

Fl3 EA3

4F
E

l1 d12

l2 d22

l3 d32

由此得 F
El
18.65kN
4

l1
d
2 1

l2
d
2 2

l3
根据式
tan 2 2I y0z0
I z0 I y0
解得主形心轴 y 的方位角为 a =
3.计算主形心惯性矩

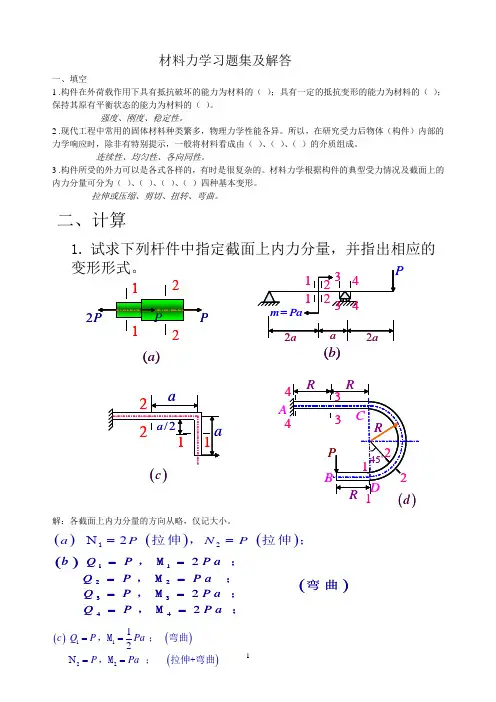
材料力学题解

材料力学题解
4 kN
在图(c)所示 N---X 坐标下,由式(a)、(b)知 N(X) 随 X 呈直线变化。由三个控制面上控制值 画出由两段斜直线构成的轴力图。见下图
C l2 2
B l1 1
A P
a
x
x2 x1
o
x / mm
N2
C
22
N1 11
A2
B
B
A1
A1
A
A
2）结构中各杆应满足各自强度条件
N1
N1
A1
1
e
N2 N2 A2 2 f
由式（e）、式(f)，有
0.518P
A1
1
P 2104 160103 61.78kN
1
0.518
由式(f) 、式（d），有
7
y
N2
45 30
C
x
P
b
0.732P
A2
2
P 3104 100103 40.98kN
四，弹性、屈服、强化和颈缩、断裂。 ５.用塑性材料的低碳钢标准试件在做拉伸实验过程中，将会出现四个重要的极限应力；其 中保持材料中应力与应变成线性关系的最大应力为（ ）；使材料保持纯弹性变形的最大应 力为（ ）；应力只作微小波动而变形迅速增加时的应力为（ ）；材料达到所能承受 的最大载荷时的应力为（ ）。
连续性、均匀性、各向同性。 3 .构件所受的外力可以是各式各样的，有时是很复杂的。材料力学根据构件的典型受力情况及截面上的 内力分量可分为（ ）、（ ）、（ ）、（ ）四种基本变形。
拉伸或压缩、剪切、扭转、弯曲。
二、计算
1. 试求下列杆件中指定截面上内力分量，并指出相应的
变形形式。
2P

材料力学ch12-3能量法三(冲击)

材料力学ch12-3能量法三(冲击)

动载分类：
惯性力： 发动机叶片 冲击载荷： 子弹、拳击 交变载荷：车轮 振动： 周期短的交变载荷
冲击过程演示
冲击变形最大位置 回弹静平衡位置
冲击末－变形最大位置
静平衡位置
冲击、回弹全过程
冲击问题简介： 冲击： 物体以一定速度作用在构件上，而且在极短的 时间内，物体速度变为零，这时，物体与构件 之间产生很大的相互作用力。 冲击载荷： 冲击时物体与构件之间的相互作用力 冲击问题非常复杂： 相互作用时间短，瞬时 冲击物和被冲击物均有变形
梁位移一般公式（计及剪力影响）
用卡氏定理计算梁位移
Vε k Fk

M ( x ) M ( x ) dx l EI Fk

kS FS ( x ) FS ( x ) dx l GA Fk
用单位载荷法计算梁位移
M 2 ( x) Vε dx l 2 EI z

l
M

F
l
S
( x )d S

l
M ( x) M ( x) kS F S ( x ) FS ( x ) dx dx l EI GA
实例与分析
已知：E/G=8/3 求 ：wB=?
1. 计算 wB


M ( x)M ( x) dx l EI
M ( x) x
FS ( x ) 1
Pl Fd l 3 v wB 3 EI 3 gEI
3
例12-3 旋转轴在A端突然被刹停，求轴内应力。轴径为 d，飞轮转动惯量为J。
解：1. 冲击惯性力偶矩计算
16 M d2 l J 2 4 G d 2
2. 冲击应力计算
M d d

材料力学习题的答案解析

材料力学习题的答案解析
B截面：
C截面：
3．若横截面由T形倒置成形时， ，∴不合理。
5-14一矩形截面简支梁由圆柱形木料锯成。已知 ， ，木材的许用正应力 。试确定当抗弯截面系数最大时矩形截面的高宽比 以及锯成此梁所需木料的最小直径d。
解：
1．作弯矩图
2．求高宽比
由 ，求得
，
∴ 抗弯截面系数最大时的高宽比为： ，此时，
3．求所需材料的最小直径
解：
1．求 和
当移动载荷F位于任一位置x时，梁的剪力图和弯矩图如图所示，
令 ，求得：当 时，
当 或 时，
2．选择截面
由正应力强度条件 ≤ ，可得
3-4承受轴力 作用的等截面直杆，若任一截面上的切应力不超过 ，试求此杆的最小横截面面积。
解：
由切应力强度条件
≤
可以得到
≥ mm2 mm2
3-5试求图示等直杆AB各段的轴力。解：为来自次超静定问题。设支座反力分别为 和
由截面法求得各段轴力分别为
， ， ①
静力平衡方程为
： ②
变形协调方程为
③
物理方程为
， ， ④
由此得到杆横截面上的应力为
MPa MPa
2．载荷
N kN
2-5图示阶梯形钢杆，材料的弹性模量 ，试求杆横截面上的最大正应力和杆的总伸长。
解：
1．最大正应力
由于杆各横截面上的轴力相同，故杆横截面上的最大正应力发生在BC段的任一横截面上，即
2．杆的总伸长
2-6图示电子秤的传感器为一空心圆筒形结构，圆筒材料的弹性模量 。在秤某一沿圆筒轴向作用的重物时，测得筒壁产生的轴向线应变 。试求此重物的重量G。
M图：
CB段： ，FQ图为水平直线，且 ，M图从左到右为向下的斜直线。

材料力学习题的答案解析

材料力学习题的答案解析
(1)静力平衡方程
：
即 ①
(2)变形协调方程：
即：
即： ②
由①②解得： kN， kN
MPa MPa
MPa MPa
3．当 且温度再上升20℃时，仍为一次超静定问题，此时静力平衡方程仍为①式，而变形协调方程为
即
即： ③
由①③解得： kN， kN
∴ MPa
MPa
第五章
5-1试用截面法求图示梁中 横截面上的剪力和弯矩。
解：
由 ：
可以得到：
即AC杆比AB杆危险，故
kN
kN
由 ：
可求得结构的许用载荷为 kN
3-4承受轴力 作用的等截面直杆，若任一截面上的切应力不超过 ，试求此杆的最小横截面面积。
解：
由切应力强度条件
≤
可以得到
≥ mm2 mm2
3-5试求图示等直杆AB各段内的轴力。
解：
为一次超静定问题。设支座反力分别为 和
解：
圆筒横截面上的轴力为
由胡克定律
可以得到此重物的重量为
第三章
拉压杆的强度计算
3-1图示水压机，若两根立柱材料的许用应力为 ，试校核立柱的强度。
解：
立柱横截面上的正应力为
所以立柱满足强度条件。
3-2图示油缸盖与缸体采用6个螺栓连接。已知油缸内径 ，油压 。若螺栓材料的许用应力 ，试求螺栓的内径。
解：
DB段， ，为向上凸的抛物线；
在距B端 截面处， ，M取极大值。
5-6图示起吊一根单位长度重量为q（ ）的等截面钢筋混凝土梁，要想在起吊中使梁内产生的最大正弯矩与最大负弯矩的绝对值相等，应将起吊点A、B放在何处（即 ）？
解：
作梁的计算简图如图（b）所示，作梁的弯矩图，图（c）所示。

大学材料力学习题及答案考试专用题型

大学材料力学习题及答案考试专用题型

一．是非题：（正确的在括号中打“√”、错误的打“×”） （60小题）1．材料力学研究的主要问题是微小弹性变形问题，因此在研究构件的平衡与运动时，可不计构件的变形。

( √ )2．构件的强度、刚度、稳定性与其所用材料的力学性质有关，而材料的力学性质又是通过试验测定的。

( √ )3．在载荷作用下，构件截面上某点处分布内力的集度，称为该点的应力。

(√ ) 4．在载荷作用下，构件所发生的形状和尺寸改变，均称为变形。

( √ )5．截面上某点处的总应力p 可分解为垂直于该截面的正应力σ和与该截面相切的剪应力τ，它们的单位相同。

( √ )6．线应变ε和剪应变γ都是度量构件内一点处变形程度的两个基本量，它们都是无量纲的量。

( √ ) 7．材料力学性质是指材料在外力作用下在强度方面表现出来的性能。

( )8．在强度计算中，塑性材料的极限应力是指比例极限p σ，而脆性材料的极限应力是指强度极限b σ。

( ) 9．低碳钢在常温静载下拉伸，若应力不超过屈服极限s σ，则正应力σ与线应变ε成正比，称这一关系为拉伸（或压缩）的虎克定律。

( )10．当应力不超过比例极限时，直杆的轴向变形与其轴力、杆的原长成正比，而与横截面面积成反比。

( √ )11．铸铁试件压缩时破坏断面与轴线大致成450，这是由压应力引起的缘故。

( )12．低碳钢拉伸时，当进入屈服阶段时，试件表面上出现与轴线成45o的滑移线，这是由最大剪应力max τ引起的，但拉断时截面仍为横截面，这是由最大拉应力max σ引起的。

( √ )13．杆件在拉伸或压缩时，任意截面上的剪应力均为零。

( ) 14．EA 称为材料的截面抗拉（或抗压）刚度。

( √ )15．解决超静定问题的关键是建立补充方程，而要建立的补充方程就必须研究构件的变形几何关系，称这种关系为变形协调关系。

( √ )16．因截面的骤然改变而使最小横截面上的应力有局部陡增的现象，称为应力集中。

(√ )17．对于剪切变形，在工程计算中通常只计算剪应力，并假设剪应力在剪切面内是均匀分布的。

材料力学 案例分析

材料力学 案例分析

广东九江大桥坍塌事故引发的争论1．主题词水平冲击，脆性破坏，设计，质询，安全隐患2．事件背景2007年6月15日，清晨5时多，广州九江大桥现场。

在漫天迷雾中一艘运沙船偏离了航道，驶向非通航的引桥。

瞬间，运沙船剧烈地撞向九江大桥桥墩，随着一声巨响，桥上的灯全灭了，紧接着又一声巨响，靠南海九江这边的桥面首先断了下去，直接砸向了运沙船。

10余秒种后，随着一声巨响，另一侧的桥面也断裂倾斜到江中。

在撞桥前，运沙船上的高音喇叭还在喊，“危险，紧急逃生……”然而，就在撞上的一瞬间，尽管运沙船做了紧急避让，向旁偏了一下，却仍然在水流的作用下将桥墩铲断……事故直接导致200米桥面坍塌，桥面上有4辆汽车坠入江中，7名司乘人员和2名巡桥工人失踪。

运沙船上的10多人落水后逃生，其中2人受伤。

专家对事故进行的技术评估尚未完成，但广东省交通主管部门一位负责人对媒体表示说，可以肯定这是一次意外事故，肇事船只未遵守航行标准，驶入非主航道造成事故发生。

九江大桥是一座斜拉桥结构的桥梁，主桥由两孔高160米的独塔混凝土斜拉桥组成，按照设计标准通航能力为3000吨。

该运沙船载重为2800多吨，船体自重1000多吨，但是水流湍急，船顺流速度超过每秒3米，其撞击力超过1000吨，而桥墩的水平防撞能力只有300吨，因此造成了事故。

图1 九江大桥事故现场3．媒体报道中提出的疑问和质询事故发生后，媒体在报道事件的同时，也纷纷刊登出评论，并针对事故原因和背后的问题提出一些疑问和质询。

大连晚报6月18日刊登了一篇新闻品评，题为“九江大桥为何如此不堪一击”。

针对广东省高速公路有限公司一位负责人关于“考虑到非通航孔被撞的可能性不大，其防撞力相对较低”的说法，评论指出，可能性不大并非没有可能，俗话还说“不怕一万，就怕万一”，按照常识，引桥的绝大部分应该是在地面上的，引桥一旦入水其桥墩和主桥墩的防撞力就没有什么区别，因为水面不同于路面，可以设置护栏和障碍。

材料力学期末考试选择填空参考题解析

材料力学期末考试选择填空参考题解析

一点的应力状态一、判断1、“单元体最大剪应力作用面上必无正应力”答案此说法错误答疑在最大、最小正应力作用面上剪应力一定为零；在最大剪应力作用面上正应力不一定为零。

拉伸变形时，最大正应力发生在横截面上，在横截面上剪应力为零；最大剪应力发生在45度角的斜截面上，在此斜截面上正应力为σ/2。

2、”单向应力状态有一个主平面，二向应力状态有两个主平面”答案此说法错误答疑无论几向应力状态均有三个主平面，单向应力状态中有一个主平面上的正应力不为零；二向应力状态中有两个主平面上的正应力不为零。

3、“受拉构件内B点的正应力为σ=P/A”答案此说法错误答疑受拉构件内的B点在α＝0度的方位上的正应力为σ=P/A。

4、“弯曲变形时梁中最大正应力所在的点处于单向应力状态。

”答案此说法正确答疑最大正应力位于横截面的最上端和最下端，在此处剪应力为零。

5、过一点的任意两平面上的剪应力一定数值相等，方向相反”答案此说法错误答疑过一点的两相互垂直的平面上的剪应力一定成对出现，大小相等，方向同时指向共同棱边或同时远离共同棱边6、“梁产生纯弯曲时，过梁内任意一点的任意截面上的剪应力均等于零”答案此说法错误答疑梁产生纯弯曲时，横截面上各点在α＝0的方位上剪应力为零，过梁内任意一点的任意截面上的剪应力不一定为零。

11、“从横力弯曲的梁上任意一点取出的单元体均处于二向应力状态“答案此说法错误答疑从横力弯曲的梁的横截面上距离中性轴最远的最上边缘和最下边缘的点取出的单元体为单向应力状态。

12、“受扭圆轴除轴心外，轴内各点均处于纯剪切应力状态”答案此说法正确答疑在受扭圆轴内任意取出一点的单元体如图所示，均为纯剪切应力状态。

选择一点的应力状态(共2页)1、在单元体中可以认为：。

A：单元体的三维尺寸必须为无穷小； B：单元体必须是平行六面体。

C：单元体只能是正方体。

D：单元体必须有一对横截面答案正确选择：A答疑单元体代表一个点，体积为无穷小。

2、滚珠轴承中，滚珠与外圆接触点为应力状态。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

击构件瞬间的速度为 υ
，只须将前面（a）式右端改为
1 2
⋅
Pυ2 g
= Vε
，即可导出 kd
=
υ2 。 g∆st
（4）、前面推导过程中，冲击物的势能取为 Ep = P(h + ∆d ) ，一般情况下 ∆d << h ，可将其忽
略，取 Ep = Ph ，读者可仿照上面推导一下，并讨论忽略后对 kd 有什么影响。
所以本问题的动载荷因数为： kd
=
∆d ∆st
=1+
1+ 2h = 1+ ∆st
1+
2
× 440 ×10 −3 2 ×10 −3 m
m
= 22
讨论：（1）、在线弹性范围内，载荷、变形、应变、应力之间都是线性关系，也就是说，当
外载荷被放大 kd 倍，则变形、应力、应变也同样被放大 kd 倍。所以有σ d = kdσ st 。有了 kd 很
动能完全转化为橡皮筋的应变能。即 Ek = Vε 。
解：设小球离开木拍瞬间速度为υ ，则其动能 Ek
=
1 2பைடு நூலகம்
W g
υ 2 ；而橡皮筋被拉至最长时应变能
Vε
=
1 2
F ⋅ ∆L ，其中
F
为小球速度为零时橡皮筋所受拉力。由于假设橡皮筋为线弹性变形，
3
所以 F
=σ
A
=
Eε
A=
∆L L0
EA ，于是Vε
=
∆d
=
∆d ∆st
P 。定义
∆d ∆st
= kd 为动载荷因数，则有
Fd P
=
∆d ∆st
= σd σ st
= kd ，将上述关系代入（d）式得： ∆d2 − 2∆st ∆d − 2∆st h = 0
解得： ∆d = ∆st (1+
1+ 2h ) ∆st
于是
kd
=
∆d ∆st
=1+
1+ 2h ∆st
冲击问题
典型习题解析
1 一圆杆横截面面积为 A ，弹性模量为 E ，杆下端带一法兰盘，杆上部套一圆形重物，如 图所示。设重物 P 离法兰盘高为 h ，当重物自由落下时，形成冲击载荷作用在杆上。试计算 杆中动应力。 解题分析：假设冲击物和杆端法兰均为刚体，则它们在冲击过程中没有应变能。同时，不考 虑其他能量损失，则，根据这一关系，即可建立冲击过程中的最大应力、变形等。 解： 重物落下后，当其达到最低点时，其势能完全转化为杆的应变能。所以有
EA 2L0
(∆L) 2
代入能量守恒方程 Ek
= Vε ，得
1 2
W g
υ2
=
EA 2L0
(∆L) 2 ，
υ=
EAg (∆L) 2 = WL0
EAg WL0
(L1
−
L0
)2
=
2.0 ×106 Pa ×1.6 ×10−6 m 2 × 9.8 m/s 2 300 ×10−3 N × 300 ×10−3 m
1+
2 × 440×10-3 2 ×10−3 m
m
= 44 ×10−3
m
= 44 mm
2、 计算动荷因数 将动载荷理解为变大了或变小了的静载荷，动载与静载之间存在特定的比例关系，
即 Fd = kdW ，其中系数 kd 即为动荷因数。
将上式两边同除以弹簧常量 k ，得到：
Fd k
=
kd
W k
， ∆d
= kd ∆st
Ep = Vε
(a)
其 中 EP 为 冲 击 物 的 势 能 。 设 受 冲 击 后 杆 的 最 大 变 形 为 ∆d ， 则
Ep = P(h + ∆d )
(b)
Vε 为杆被冲击后的应变能，设重物对杆冲击作用的最大作用力为 Fd ，
则 Fd 做的功即为杆增加的应变能。
所以， Vε
=
1 2
Fd ∆d
于是由（a），（b），（c）三式有
空心柱体
外力功。 解：1、计算弹簧最大位移
题2图
设弹簧被冲击后，最大位移为 ∆d ，弹簧承受的最大冲击力为 Fd ，则由能量守恒得
W (h
+
∆d
)
=
1 2
Pd
∆d
。
由于弹簧常量为 k ，所以有 W = k∆st ， Pd = k∆d 。 ∆st 为重物静止放在弹簧上时弹簧
的缩短量。于是有
W (h
+
∆d
方便就能计算出动载荷条件下被冲击物的各量。（2）、但应注意，对不同的问题， kd 有不同 的表达式，不能生搬硬套。（3）、掌握本题所采用的以能量守恒为基本原理的分析方法是最 重要的。
3 一个橡胶小球重W = 300 mN ，用一橡皮筋连在一木拍上，橡皮筋长 L0＝300 mm ，横截
面面积 A = 1.6 mm2 ，弹性模量 E = 2.0 MPa 。用木拍击打小球后，小球拉动橡皮筋，使橡
(c) 题1图
P(h +
∆d )
=
1 2
Fd ∆d
，或
Fd ∆d
− 2P∆d
− 2Ph
=
0
(d)
对线弹性体，载荷与其相应位移存在关系 P = k ⋅ ∆st ， k 为刚度系数。 ∆st 为载荷 P 作用
下杆的位移。设杆长为 l
，则
∆st
=
Pl EA
。动载荷时，同样有 Fd
=
k∆d
于是有 Fd
=
P ∆st
2 如图所示柱筒内重为 W = 20 N 重物从高为 h = 440 mm 处落到一个弹簧上，弹簧常量
k = 10 kN/m 。（1）确定弹簧的最大压缩位移；（2）
重物
计算动荷因数。
解题分析：忽略重物在冲击过程中的变形，并忽略
h
能量损失，则重物冲击弹簧后，其势能全部转化为
弹簧
弹簧应变能，利用能量守恒原理，则有 Ep = Vε ，Vε =
皮筋总长达到 L1 = 1.0 m ，试问小球离开木拍瞬间的速度是多少？假设橡皮筋为线弹性体， 而且忽略小球的势能。 解题分析：木拍击打小球是冲击载荷问题。小球受木拍撞击飞出，将连接小球和木拍的橡皮 筋拉长。小球离开木拍的瞬间有一个初速度，橡皮筋被拉长的同时，小球速度不断减小，当 小球速度为零时，橡皮筋被拉至最长。假设不考虑小球的势能变化，则小球离开木拍瞬间的
)
=
1 2
k∆d
⋅
∆d
即
k∆d2 − 2W∆d − 2Wh = 0 或 ∆d2 − 2∆st ∆d − 2∆st h = 0 。解得
∆d = ∆st (1+
1+ 2h ) ∆st
2
而 ∆st
=W k
= 20 N 10 ×103 N/m
= 2 ×10 −3
m
代入前式得
∆d = 2 ×10−3 m(1+
1
有了动荷因数后，可用下面式子计算动载荷作用下构件的变形和应力。
冲击载荷： Fd = kd P
冲击位移： ∆d = kd ∆st
冲击应力，即杆中的动应力：σ d
=
kdσ st
=
kd
P A
讨论： (1)、冲击载荷或其他动载荷作用下构件变形和应力计算可归结为计算动荷因数 kd ，
算出 kd 后，只要将相应的静载荷下的变形和应力乘以 kd ，即得到动载荷作用下构件的变形 和应力。(2)、当 h = 0 时，为突加载荷情况，这时 kd = 2 。(3)、水平冲击问题：设冲击物撞