“等价关系”部分习题参考答案
- 格式:doc
- 大小:34.00 KB
- 文档页数:4

抽象代数等价关系习题答案抽象代数等价关系习题答案抽象代数是数学中的一个重要分支,研究的是代数结构的一般性质和规律。
在抽象代数中,等价关系是一个基本概念,它描述了两个元素之间的相等性。
在本文中,我将为大家提供一些抽象代数中等价关系习题的答案,希望能对大家的学习有所帮助。
1. 设A是一个非空集合,R是A上的一个等价关系。
证明:对于任意的a ∈ A,[a] = A。
解答:根据等价关系的定义,[a]是由所有与a等价的元素组成的集合。
而等价关系具有自反性,即对于任意的元素a,a与自身等价。
因此,a ∈ [a],即a属于[a]中的元素。
又因为R是等价关系,所以对于任意的b ∈ A,若a与b等价,则b与a也等价。
因此,[a]中的任意元素与a都等价,即[a]包含了A中的所有元素。
综上所述,[a] = A。
2. 设A是一个非空集合,R是A上的一个等价关系。
证明:对于任意的a, b ∈ A,若a与b等价,则[a] = [b]。
解答:假设a与b等价,即(a, b) ∈ R。
根据等价关系的定义,对于任意的c ∈ [a],都有(c, a) ∈ R。
由于(a, b) ∈ R,根据等价关系的传递性,对于任意的c ∈ [a],都有(c, b) ∈ R。
因此,[a]的任意元素与b都等价,即[b] ⊆ [a]。
同理可证,[a] ⊆ [b]。
综上所述,[a] = [b]。
3. 设A是一个非空集合,R是A上的一个等价关系。
证明:对于任意的a, b ∈ A,若[a] ∩ [b] ≠ ∅,则[a] = [b]。
解答:假设[a] ∩ [b] ≠ ∅,即存在一个元素c,使得c ∈ [a] 且c ∈ [b]。
根据等价关系的定义,对于任意的d ∈ [a],都有(d, a) ∈ R。
由于c ∈ [a],根据等价关系的传递性,对于任意的d ∈ [a],都有(d, c) ∈ R。
同理可证,对于任意的d ∈ [b],都有(d, c) ∈ R。
因此,[a]和[b]中的任意元素与c都等价,即[a] ⊆[b] 且 [b] ⊆ [a]。

等价关系证明题【原创实用版】目录1.等价关系证明题的概念和分类2.等价关系证明题的解题方法3.等价关系证明题的例题解析4.总结与展望正文一、等价关系证明题的概念和分类等价关系证明题是数学中一种常见的题型,主要涉及到集合、方程、不等式等数学概念的等价关系的证明。
等价关系证明题可以分为以下几类:集合相等、集合包含关系、方程根的等价关系、不等式解集的等价关系等。
二、等价关系证明题的解题方法1.集合相等关系的证明:通常采用元素与集合关系的互证方法,即证明两个集合的元素具有一一对应的关系。
2.集合包含关系的证明:可以采用直接证明和反证法两种方法。
直接证明是证明集合 A 中的任意元素都属于集合 B;反证法是假设集合 A中有元素不属于集合 B,然后推导出矛盾。
3.方程根的等价关系证明:通常采用代数方法,将方程的根与等价条件建立起代数关系,然后证明这个代数关系成立。
4.不等式解集的等价关系证明:可以采用代数方法、几何方法等多种方法,关键是将不等式的解集与等价条件建立起代数关系或几何关系。
三、等价关系证明题的例题解析例题:证明集合 A={x|x^2-3x+2=0}与集合 B={1,2}是相等关系。
解析:首先解出集合 A 中的元素,得到 A={1,2},然后证明 A 与 B 的元素具有一一对应的关系,即 A 中的任意元素都属于 B,B 中的任意元素都属于 A。
因此,集合 A 与集合 B 是相等关系。
四、总结与展望等价关系证明题是数学中常见的题型,涉及到多种数学概念的等价关系的证明。
解决这类问题需要掌握一定的数学方法和技巧,如元素与集合关系的互证方法、直接证明与反证法、代数方法等。
在实际解题过程中,还需要灵活运用这些方法和技巧,提高解题效率。

§1.1 集合1、 设A B ⊆ ,证明:A B A = ,A B B = .证明:由A B ⊆,可知A 的所有元素都属于B ,既A 的所有元素,都是A 和B 的共同元, 则由交集定义可知 A A B ⊆ . 又A B A ⊆ ,所以A B A = .由并集定义知,A B 的所有元素,都属于A 或B ; 又A B ⊆,所以A B 的所有元素都属于B ,即A B B ⊆. 又B A B ⊆,故A B B =2、 设B ,()i A i I ∈ 均为集合Ω 的子集,试证:()1 ()i i i I i I B A B A ∈∈⎛⎫=⎪⎝⎭ ()2 ()i i i I i IBA B A ∈∈⎛⎫=⎪⎝⎭ 证明:()1 由定义i i Ix B A ∈⎛⎫∈⎪⎝⎭当且仅当x B ∈且x 属于某一i A ;当且仅当x 属于某一i B A ;当且仅当()i i Ix B A ∈∈.()2 由定义i i I x BA ∈⎛⎫∈⎪⎝⎭当且仅当x 属于B ,或x 属于任一i A ,i I ∈;当且仅当x 属于任一i B A ,i I ∈;当且仅当()i i Ix B A ∈∈.§1.2 等价关系1、设为整数集,问以下各关系是否为M 的等价关系?1)0aRb ab ⇔≥ 2)4aRb a b ⇔+ 3)aRb a b ⇔= 4)220aRb a b ⇔+≥ 解:1)不是,因为不满足传递性2)不是,不满足反身性和传递性 3)是 4)是2、试指出上题中等价关系所决定的分类.解:3)每个元素是一个类 4)整个整数集作成一个类 3、找出下列证明中的错误:若S 的关系R 有对称性和传递性,则必有反身性.这是因为,对任意的a S ∈ ,由对称性,如果aRb ,则bRa .再由传递性,得aRa ,所以R 有反身性.解:以上证明过程中只考虑了当aRb 成立的情况,但是当对于元素a ,不存在b 使aRb 成立时,aRa 就不能得到.4、在复数集中,规定关系"" :a b a b ⇔=. (1)证明:是的一个等价关系;(2)试确定相应的商集,并给出每个等价类的一个代表元素.(1)证明:设a ,b ,c ∈ ,则()a 因为aa =,所以a a ,于是 是有反身性;()b 若ab ,则a b =,于是b a =,从而b a ,说明是具有对称性;()c 若ab ,bc ,则a b =,b c =,于是a c =,从而a c ,从而具有传递性.所以是的一个等价关系.(2)解:相应的商集[]{}0r r R r =∈≥且,其中[]{}()[]{}cos sin 0,2r x x r r i θθθπ=∈==+∈对任意的c ∈ ,等价是[]c :代表元素可取作c .§1.31、{}1,2,,100S = ,找一个A A ⨯到A 的映射.解:设(),a b 表示A A ⨯的任意元素,,a b A ∈ ,则作映射:f A A A ⨯→ ,()(),f a b b = .f 是一个A A ⨯到A 的映射.2、设A ,B 是两个有限集合,则(1)A 到B 的不同映射共有多少?(2)A 到B 的单射共有多少个?解:(1)设A n = , B m =,则A 到B 的映射有n m 个 (2)设A n = , B m =,若n >m ,则A 到B 没有单射; 若n m ≤,则A 到B 有()!!m m n - 个单射. 3、设x 是数域F 上全体n (n >1)阶方阵作成的集合.问::A A ϕ→是否为x 到F 的一个映射?其中A 为A 的行列式,是否为满射或单射?解:ϕ 是映射,且是满射,但不是单射4、设:f A B →为双射,则f 的逆映射1:f B A -→也是一个双射且()11f f --=.证明:设()() ,f x y x A y B =∈∈ ,则1:f y x -→,即()1f y x -=, 因f 是A B →的双射, 所以1f -是B 到A 的双射, 且1f -的逆映射就是f ,即()11ff --=.5、设:f A B →,:g B C →为两个双射到:g f A C → 也是双射且()111g f f g ---= .证明:()()11111B C g f f g g g ---⋅⋅==,()()111111B A fg gf f f ----==,故g f 也是双射,且()111gf f g ---= .§1.41、设A 是一个有限集合,则A 上不同的二元运算共有多少个?解:设A n = ,则2A A n ⨯= ,故A A ⨯到A 有2n n 个不同的映射. 即A 上有2n n 个不同的二元运算.2、{},,A a b c = ,规定A 的两个不同的代数运算.解:()a 第一个代数运算() , ,R x y a xRy x y A →=∀∈ ()b 第二个代数运算() , ,R x y y xRy x y A →=∀∈3、设M 为整数集,问()22 ,a b a b a b M =+∀∈是否满足结合律和交换律.解:交换律满足,但结合律不满足.例如()1104=,()1102= 4、设M 为实数集,问:23a b a b =+ (),a b M ∀∈是否满足结合律和交换律.解:都不满足.例()1004=,()1002=,故()()100100≠,又102=,013=,故1001≠.5、数域F 上全体非零多项式的集合对于()()()()(),f x g x f x g x =是否满足结合律和交换律?其中()()(),f x g x 表示()f x 与()g x 的首项函数为1的最大公因式.解:显然是代数运算且满足交换律.又结合律也满足,因为根据最大公因式的性质知:())()(()()(),,,,f g h f g h f g h f g h ===§2.11、有限群中每个元素的阶都是有限的。

集合论--等价关系、函数部分自测题(答案)一、选择题1、设R和S是集合A上的等价关系,则R∪S的对称性( )(1)一定满足;(2)一定不满足;(3)不一定满足;(4)不可能满足.答案:〔(1)〕.2、设R1和R2是非空集A上的等价关系,下述各式哪个是等价关系( )(1)(A×A)-R1;(2)R21;(3)R1-R2;(4)r(R1-R2).答案:〔(2)〕.3、设集合A中有4个元素,则A上的不同的等价关系的个数为( )(1)11个; (2)14个;(3)15个; (4)17个.答案:〔(3)〕.4、对任何a∈A,形成的A上的等价关系R的等价关系(a)R为( )(1)空集; (2)非空集(3)是空集也可为非空集(4){x|x∈A}.答案:〔(2)〕.5、集合A上的等价关系R,其等价类集合{〔a〕R|a∈A}称为( )(1)A与R的并集,记作A∪R(2)A与R的交集,记作A∩R(3)A关于R的商集,记作A/R(4)A与R的差集,记作A-R.答案:〔(3)〕.6、集合A上的等关系R,决定了A的一个划分,该划分就是( )(1)并集A∪R; (2)交集A∩R;(3)差集A-R; (4)商集A/R答案:〔(4)〕.7、设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为( )(1)2+3个; (2)23个;(3)2×3个;(4)32个.答案:〔(2)〕.8、 52张扑克牌分配给4个桥牌比赛者进行比赛,扑克牌集合A到桥牌比赛者集合B的函数f:A→B为( )(1)单射函数; (2)双射函数;(3)满射函数; (4)一个映射.答案:〔(3)〕.9、集合R上的函数“…是取…的平方”为R→R的( )(1)映射; (2)单射;(3)满射; (4)双射.答案:〔(1)〕.10、若f、g都是满射的,则复合函数fog必是( )(1)映射; (2)入射;(3)满射; (4)双射.答案:〔(3)〕.11、映射的复合运算满足( )(1)交换律; (2)结合律;(3)幂等律; (4)分配律.答案:〔(2)〕.12、设f和g都是从A到A的双射函数,则(fog)-1为( )(1)f-1og-1;(2)fog-1;(3)(gof)-1;(4)g-1of-1答案:〔(4)〕.二、填空题1、设R为集合A上的等价关系,对任何a∈A,集合〔a〕R= ,称为元素a形成的R等价类;〔a〕R≠φ,因 .答案:〔{x|x∈A,aRx};至少有a∈〔a〕R〕2、集合A上的等价关系R,其等价类集合称作A关于R的商集,记作 .答案:〔{a}R|a∈A;A/R〕.3、设10人集合E={赵茵,赵小滨,孙丽春,赵萍,钱洁,李靖华,李秀娟,钱钰,李惠芝,李莉}上的同姓关系为R,则等价类赵·= ,钱·= ,孙·= ,李·= ,而商集E/R= .答案:〔{赵茵,赵萍};{钱小滨,钱洁,钱钰};{孙丽春};{李靖华,李秀娟,李惠芝,李莉};{赵·,钱·,孙·,李·}〕4、根据集合A上的等价关系R与划分之间的关系,推知R可确定,A的一个划分可确定 .答案:〔A的一个划分;A的一个等价关系〕.5、设f:a称b为父亲,g:b称c为父亲,则fog: .答案:答案:〔a称c为祖父〕.6、设f:a称b为母亲,b:b称c为父亲,则fog: .答案:答案:〔a称c为外祖父〕.7、设f:a称b为父亲或母亲,f1:b称c为子或女,则fof1 .答案:〔a是c的兄弟或姐妹,或者a和c是同一个人〕..8、设函数f:A→B有逆函数f-1:B→A,则f-1of= ,fof-1= .答案:〔I B; I A〕.9、设gof是一个复合函数.(1)若g和f是满射的,则gof为 .(2)若g和f是入射的,则gof为 .(3)若g和f是双射的,则gof为 .答案:〔满射的;入射的;双射的〕.10、设映射f:A→B,g:B→C,且g和f是满射,则fog为;若g和f是双射,则fog为且(fog)-1= .答案:〔满射;双射;g-1of-1〕.三、判断题1、平面上直线间的平行关系||是等价关系.答案:〔y〕.2、数集A上的不等关系≠可确定A的一个划分.答案:〔N〕.3、某妇人的子女构成的集合A中,关系R:……与……姐妹,能得到A的一个划分.答案:〔N〕.4、数集A中的整除关系|,能得到A的一个划分.答案:〔N〕.5、一个关系,如果它的图示的始集A的每个点能作一条矢线且仅作一条矢线到终集B 的一个点,称这个关系为函数.对吗?答案:〔y〕.6、若有f(A)=B的映射f:A→B,则称此f为满射.答案:〔y〕.7、映射f:A→B,当值域B*=B时,为满射.答案:〔y〕.8、映射f:A→B,若B中的点至多只有一条f的矢线可以到达,则称f为单射.答案:〔y〕.9、映射f:A→B,若对每一个a∈A,b∈A,有a≠b f(a)≠f(b),则称f为单射.答案:〔y〕.10、对于映射f:A→B,当f-1:B→A也是映射时,则称此f为双射.答案:〔y〕.11、映射f:A→B是双射的充分必要条件是,从A的每一点有且仅有一条矢线可引出,在B的每一点有且仅有一条矢线到达.答案:〔y〕.12、双射函数就是满射函数.答案:〔N〕.13、双射是一一对应的,它的逆不一定一一对应.答案:〔N〕.14、函数f、g、h可以复合,但fo(goh)≠(fog)oh答案:〔N〕.15、若f:A→B,g: B→C是双射函数,则(gof)-1=g-1of-1.答案:〔N〕.16、若f:Z→N,则f(i)=|3i|+1是双射函数i∈Z.答案:〔N〕.17、关于f={<n,m>|m∈N,n+m<10}是函数.答案:〔N〕.18、函数f:N→R,f(n)=lgn是满射的.答案:〔N〕.19、函数f:R→R,f(x)=x2,它存在逆函数f-1.答案:〔N〕.20、函数f:R→R,f(x)=x3+2,则f-1(x)=x-2.答案:〔N〕.。



等价关系证明题摘要:1.等价关系证明题的概述2.等价关系的基本性质3.证明等价关系的方法4.举例说明等价关系证明题的解法正文:一、等价关系证明题的概述等价关系证明题是数学中一种常见的题目类型,主要考察学生对等价关系的理解和应用。
等价关系是指两个数学表达式在某些特定条件下具有相同的值,通过证明等价关系,可以加深对数学概念的理解,提高解题能力。
二、等价关系的基本性质等价关系具有以下几个基本性质:1.自反性:对于任意的x,x 与x 等价。
2.对称性:如果a 与b 等价,那么b 与a 也等价。
3.传递性:如果a 与b 等价,b 与c 等价,那么a 与c 也等价。
三、证明等价关系的方法证明等价关系的方法主要有以下几种:1.代入法:将等价关系的一个表达式代入另一个表达式,证明它们的值相等。
2.恒等变形法:对等价关系的两个表达式进行恒等变形,最终证明它们的值相等。
3.反证法:假设等价关系的两个表达式的值不相等,然后通过推理证明这个假设是错误的。
四、举例说明等价关系证明题的解法例如,证明以下等价关系:x^2 + 2x + 1 = (x + 1)^2解法:1.代入法:将x^2 + 2x + 1 代入(x + 1)^2,得到:(x + 1)^2 = (x + 1) * (x + 1) = x^2 + 2x + 1因此,x^2 + 2x + 1 与(x + 1)^2 等价。
2.恒等变形法:对x^2 + 2x + 1 和(x + 1)^2 进行恒等变形,得到:x^2 + 2x + 1 = x^2 + 2x + 1(x + 1)^2 = x^2 + 2x + 1因此,x^2 + 2x + 1 与(x + 1)^2 等价。
通过以上证明,我们可以得出结论:x^2 + 2x + 1 与(x + 1)^2 是等价关系。
总之,掌握等价关系的基本性质和证明方法,可以帮助我们更好地解决等价关系证明题。

1.4.3-命题的形式及等价关系(含答案)本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March1.4.3 命题的形式及等价关系【课堂例题】例1.判定下列两个命题是否等价:(1)命题A:“4是偶数”,命题B:“4是2的整数倍”.(2)命题A:“两组对边分别平行的四边形是平行四边形”;命题B:“有一组对边平行且相等的四边形是平行四边形”.(3)命题A:“如果a b =,那么ac bc =”;命题B:“如果a b ≠,那么ac bc ≠”.(4)命题A:“如果a b =,那么ac bc =”;命题B:“如果ac bc =,那么a b =”.例2.利用等价命题,判断下列命题的真假:(1)如果2230x x --≠,那么1x ≠-且3x ≠;(2)如果a b +不是偶数,那么,a b 不都是偶数;(3)如果0x y +≤或者0xy ≤,那么0x ≤或者0y ≤;(4)如果x AB ∉,那么x A ∉且x B ∉.例3. 若22323420x xy y x y +++++≠,求证:10x y ++≠例4.利用反证法证明:(1)已知实数,,a b c 满足1a b c ++=,求证:,,a b c 中至少有一个不小于13;(选用是无理数.1.4.3 命题的形式及等价关系【知识再现】1.如果,A B 是两个命题,满足 且 ,那么,A B 叫做等价命题,记作 .2.原命题必然与 是等价命题;原命题的否命题必然与 是等价命题.3.反证法是通过假设 不成立,经过一系列推理得出结论与已知条件、定理等矛盾,从而说明假设不成立,原命题成立的一种间接证明法.【基础训练】1.写出下列命题的一个等价命题:(1)“若1x <-,则||1x >” ;(2)“若,x y 都不为零,则0xy ≠” ;(3)“能被10整除的数必能被5整除”.2.已知语句α与语句β的关系是:αβ⇒,则下列必定正确的推出关系是( )A.αβ⇒;B.αβ⇒;C.βα⇒;D.βα⇒;3.利用等价命题,判断下列命题的真假:(1)若(2)(4)0--≠x y ,则2≠x 且4≠y ;( )(2)若4+≤x y 或4xy ≤,则2≤x 或2y ≤;( )(3)若,a b 不都是偶数,则a b +不是偶数. ( )4.(1)由命题甲成立,可以推出命题乙不成立,下列说法一定正确的是( ).(A)命题甲不成立,可以推出命题乙成立;(B)命题甲不成立,可以推出命题乙不成立;(C)命题乙成立,可以推出命题甲成立;(D)命题乙成立,可以推出命题甲不成立.(2)以下说法错误的是( ).(A)如果一个命题的逆命题为真命题,那么它的否命题也必为真命题;(B)如果一个命题的否命题为假命题,那么它本身一定是真命题;(C)原命题、否命题、逆命题、逆否命题之中,真命题的个数一定为偶数;(D)一个命题的逆命题、否命题、逆否命题可以同为假命题.5.试判断命题A:“在ABC ∆中,222BC AC AB =+”与命题B:“ABC ∆是直角三角形”是否为等价命题,并说明理由.6.如图,已知四边形ABCD 的对角线交于点求证:若对角线,AC BD 不互相平分,则四边形ABCD 不是平行四边形.7.若22320a b a b --++≠,求证:2a b +≠【巩固提高】8.试判断命题A:“三角形任意两边之和大于第三边”与命题B:“三角形任意两边之差小于第三边”是否为等价命题,并说明理由.9.是无理数.(选做)10.(1); 若2220a b c ab bc ac ++---≠,求证:,,a b c 中至少有两个不相等.(2)已知,a b.提示: 10.(2)a b =- 【温故知新】11.类比A B A B A ⊆⇔=,再写两个:A B ⊆⇔ ;A B ⊆⇔ .【课堂例题答案】例1.是,是,否,否例2.真,真,假,假例3.证:101x y y x ++=⇒=--⇒2222323423(1)2(1)34(1)20x xy y x y x x x x x x +++++=+--+--++--+= 原命题的逆否命题成立,因此原命题成立 证毕例4.(1)证:假设111,,333a b c <<<, 111111,,333333a b c a b c <<<⇒++<++1a b c ⇒++< 与条件矛盾,因此假设不成立,即,,a b c 中至少有一个不小于13. 证毕 (2)Q,,m m n n=互质 222m n =⇒2m 是偶数m ⇒是偶数⇒2,m k k Z =∈2222(2)22k n k n ⇒=⇒=⇒ 2n 是偶数n ⇒是偶数是无理数. 证毕【知识再现答案】1.,,A B B A A B ⇒⇒⇔2.原命题的逆命题,原命题的否命题.3.待证命题的结论不成立.【习题答案】1.(1)若||1x ≤,则1x ≥-;(2)若0xy =,则,x y 中至少有一个为零;(3)不能被5整除的数必定不能被10整除.3.真,真,假4.(1) D ;(2) B5.不等价,A B ⇒,B A ⇒/,因为ABC ∆是直角三角形⇒/90A ︒∠=6.证:四边形ABCD 是平行四边形 //,//AB DC AD BC ⇒ 12()43BD DB ADB CBD ASA ⎧∠=∠⎫⎪⎪⇒=⇒∆≅∆⎨⎬⎪⎪∠=∠⎭⎩AB DC ⇒= 12∠=∠ (),ABO COD ASA AO CO BO DO ⇒∆≅∆⇒== 56∠=∠,AC BD ⇒互相平分 原命题的逆否命题成立,因此原命题成立. 证毕7.证:证明逆否命题 2222(2)3(2)20a b b a a a a a +=⇒=-⇒---+-+=逆否命题成立,因此原命题成立. 证毕8.等价.证:设三边为,,a b c:A “三角形任意两边之和大于第三边”,:B “三角形任意两边之差小于第三边” 若,a b c c a b c b a +>⇒-<-<,同理:,a c b b a c b c a +>⇒-<-<;,b c a a c b a b c +>⇒-<-< 因此A B ⇒;反之,若,,,,,c a b c b a b a c b c a a c b a b c -<-<-<-<-<-<则,,a b c a c b b c a +>+>+>因此B A ⇒;综上:A B ⇔ 证毕⎫⎪⎬⎪⎭9.证:反证法.Q n m=,且,m n 互质 223m n =⇒2n 是3的倍数⇒n 是3的倍数⇒2n 是9的倍数,又223n m =⇒2m 是3的倍数⇒m 是3的倍数,与,m n 互质矛盾 . 证毕 10.(1)证:证明逆否命题.2220a b c a b c ab bc ac ==⇒++---=,逆否命题成立,那么原命题成立. 证毕提示:直接证明可以利用222()()()0a b b c c a -+-+-=(2)证:反证法是有理数,=a b -都是有理数⇒2Q +=∈与已知矛盾,. 证毕11.A B ;对于任意x A ∈,成立x B ∈;U U A B ⊇……答案不唯一。

离散数学习题答案习题一及答案:(P14-15)14、将下列命题符号化:(5)李辛与李末是兄弟解:设p:李辛与李末是兄弟,则命题符号化的结果是p(6)王强与刘威都学过法语p q解:设p:王强学过法语;q:刘威学过法语;则命题符号化的结果是(9)只有天下大雨,他才乘班车上班q p解:设p:天下大雨;q:他乘班车上班;则命题符号化的结果是(11)下雪路滑,他迟到了解:设p:下雪;q:路滑;r:他迟到了;则命题符号化的结果是(p q)r15、设p:2+3=5.q:大熊猫产在中国.r:太阳从西方升起.求下列复合命题的真值:(p q r)((p q)r)(4)解:p=1,q=1,r=0,(p q r)(110)1,((p q)r)((11)0)(00)1 (p q r)((p q)r)111 19、用真值表判断下列公式的类型:(p p)q(2)解:列出公式的真值表,如下所示:p p qq(p p)(p p)q0 0 1 1 1 10 1 1 0 1 01 0 0 1 0 11 1 0 0 0 1由真值表可以看出公式有3个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值:(4)(p q)q解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:p0(p q) 1q0q0成真赋值有:01,10,11。
所以公式的习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值:(2)(p q)(q r)解:原式(p q)q r(p p)q rq r,此即公式的主析取范式,m m(p q r)(p q r)37所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值:(2)(p q)(p r)解:原式,此即公式的主合取范式,M(p p r)(p q r)(p q r)4所以成假赋值为100。
7、求下列公式的主析取范式,再用主析取范式求主合取范式:(1)(p q)r解:原式p q(r r)((p p)(q q)r)(p q r)(p q)r(p q)r(p q)r(p q)r(pq r(p q r)(p q)r(p q)r(p q)r(pq r,此即主析取范式。

ln1等价代换的题【原创实用版】目录1.等价代换的定义与概念2.等价代换的类型与应用3.等价代换的解题技巧与方法4.等价代换的实际应用案例5.总结与展望正文一、等价代换的定义与概念等价代换是数学中一种重要的代数变换,指的是将一个数学式子中的某些元素用其他元素表示,使得整个式子的值不变。
这种变换在解决许多数学问题时都具有非常重要的意义,尤其是在代数方程、不等式以及函数等领域中。
二、等价代换的类型与应用等价代换主要有以下几种类型:1.变量代换:将一个变量用另一个变量表示,如将 x 用 y 表示,这种代换常常用于简化方程或不等式。
2.函数代换:将一个函数用另一个函数表示,如将 f(x) 用 g(x) 表示,这种代换常常用于化简函数表达式或求解函数的性质。
3.矩阵代换:将一个矩阵用另一个矩阵表示,这种代换常常用于简化矩阵计算或求解矩阵的性质。
等价代换在数学问题的解决中具有广泛的应用,例如在解方程、证明不等式、化简函数等方面都会用到等价代换。
三、等价代换的解题技巧与方法进行等价代换时,需要注意以下几点:1.保持等价:代换后的表达式与原表达式的值相等。
2.简化问题:代换后的表达式要更容易求解或理解。
3.便于计算:代换后的表达式要更便于进行计算。
4.根据具体情况选择适当的代换类型。
四、等价代换的实际应用案例例如,在解方程 x^2 + ax + 1 = 0 时,我们可以使用等价代换,将x^2 + ax + 1 表示为 (x + 1/2a)^2 + 3/4a^2 - 1/4a^2 = 0,这样方程就变得容易求解。
五、总结与展望等价代换是数学中一种重要的代数变换,对于解决许多数学问题都具有重要的意义。
了解等价代换的定义与概念,掌握等价代换的类型与应用,熟练运用等价代换的解题技巧与方法,是每一个数学学习者都需要具备的基本能力。
“等价关系”部分习题参考答案《二元关系》部分习题参考答案3.5 等价关系和划分(P129)第2题证明:?x∈A,∈R;?∈R,∈R;?∈R,∈R,则有∈R,所以R 是自反的、对称的、传递的,因而R 是等价关系。
第3题解:(1)A上最大等价关系是全域关系,故其元素个数为n2个。
(2)A上最大等价关系的秩是1。
(3)A上最小等价关系是相等关系,故其元素个数为n个。
(4)A上最小等价关系的秩为n。
第5题解:(a)不是等价关系。
因为A?A-R1不具有自反性。
(b)也不是等价关系。
也不具有自反性。
(c)是等价关系。
(d)不是等价关系。
(e)不是等价关系。
第7题解:(a)R=“<”不是等价关系,因为<不具有自反性和对称性。
R 诱导的等价关系全域关系。
(b)它不是等价关系。
因为<0,0>?R,所以不具有自反性。
R诱导的等价关系是R?<0,0>。
(c)它不是等价关系。
因为<0,0>?R,故它不具有自反性,有<0,1>∈R,但<1,0>?R,故它不具有对称性。
R诱导的等价关系是:{|(a≥0∧b≥0)∨(a≤0∧b≤0)}(d)它不是等价关系。
因为<0,0>?R,所以不具有自反性。
(e) 它不是等价关系。
因为R不具有对称性。
R诱导的等价关系为I上的全域关系。
第10题解:A的所有划分如下:π1={{a,b,c}} π2={{a},{b,c}}π3={{b},{a,c}} π4={{c},{a,b}} π5={{a},{b},{c}}的哈斯图为:第11题解:(a) π1所诱导的等价关系的序偶为:R1={,,,,,,,,,} (b) π2和π3诱导的等价关系分别是:R2={,,,}R3=A?A(c){{ π1, π2, π3},细分}的哈斯图为:第12题解:(a)如果π1=π2,则π1?π2是A的划分,其他情况不是A的划分。
(b)如果π1=π2,则π1?π2是A的划分,其他情况不是A的划分。
一、选择题1.“以物换物”这种古老的交易方式,随着网络技术的发展日渐流行。
采用这种交易方式的人们自称“换客”,他们用自己的闲置物品来换取自己需要的东西。
这种交易方式( )①不必遵循等价交换原则②不需要以一般等价物为媒介③是古代商品流通形式的回归④“买”和“卖”是同一个过程A.①②B.③④C.①③D.②④2.下列关于货币和一般等价物关系的认识,正确的是①两者是同时出现的②两者都能表现其他商品的价值③货币的本质就是一般等价物④只有货币才能充当一般等价物A.①②B.①④C.②③D.③④3.在我国商品市场上,人们都是用人民币购买商品,这说明A.人民币的本质是货币,能执行流通手段职能B.人民币在商品交换中起媒介作用C.人民币是商品,有价值D.人民币在本质上是一般等价物4.中国人民银行定于2019年7月10日以国家法定货币形式发行金银纯度均为99.9%的第七届世界军人运动会金银纪念币。
下列对该纪念币认识正确的是①与商品是一对孪生兄弟,同时产生②它充当商品交换的媒介,是一般等价物③是商品交换发展到一定阶段的产物④是从商品中分离出来充当等价物的商品A.①③B.①④C.②③D.②④5.2019年8月我国央行相关负责人表示,我国未来推出的数字货币将是对流通现金具有一定替代性的全新加密电子货币体系,可以脱离传统银行账户实现价值转移,使交易环节对账户依赖程度大为降低。
这表明我国研究的数字货币①将改变货币原有的基本职能②相比于传统电子货币流通更便利③基于国家信用并由其统一发行④发行目的是对我国流通现金的升级和替代A.①③B.①④C.②③D.②④6.2018 年 8 月 8 日,中国人民银行发行中国能工巧匠金银纪念币。
本次发行的这套金银币共两枚,包括 5 克金币(中国能工巧匠•鲁班)和 15 克银币(中国能工巧匠•样式雷)各一枚,均为中华人民共和国法定货币,最大发行量 1 万枚。
它成功地让古圣先贤的伟大创造在现代国家法定货币上重现生机。
一、选择题1.在“商品—货币—商品”的流通过程中,“商品—货币”阶段的变化“是商品的惊险的跳跃。
”这个跳跃如果不成功,摔坏的不是商品,而是商品所有者。
这说明()A.货币作为商品交换的媒介必须是观念上的货币B.商品生产者生产的商品就是失去了使用价值和价值C.商品生产者需要生产适销对路、质量上乘的商品D.货币作为一般等价物在物物交换中起决定作用2."金性不败朽,故为万物宝”,正因为如此,在长期的商品交换过程中,金银逐渐固定地充当了一般等价物,成为各国普遍接受的货币。
下列说法正确的是①金银具有最适合充当一般等价物的特性②因为各国普遍接受金银,所以产生了货币③货币是商品交换发展到一定阶段的产物④在商品交换中,等价物总是固定在金银上A.①② B.①③ C.②④ D.③④3.电视纪录片《货币》在片头这样写道:“它在今天人们的心中,仿佛是空气、是水、是阳光,是陪伴人一生的东西…人们知道她从哪里来,但不知道她到哪里去。
她就是神奇而陌生的货币”。
货币之所以神奇,最根本的原因是A.货币能买到人们所需要的一切B.货币具有体积小、价值大、易保存特点C.货币的本质是一般等价物D.货币是商品交换发展到一定阶段的产物4.在我国商品市场上,人们都是用人民币购买商品,这说明A.人民币的本质是货币,能执行流通手段职能B.人民币在商品交换中起媒介作用C.人民币是商品,有价值D.人民币在本质上是一般等价物5.中国人民银行发行的庆祝改革开放40周年纪念币(如右图)为中华人民共和国法定货币。
该纪念币在本质上是( )A.劳动产品B.无差别的人类劳动 C.价值尺度D.一般等价物6.在超市,我们随处可见各种商品及其标价,如某品牌矿泉水1.5元,某品牌凉茶3.5元……这里的1.5元和3.5元()①是商品价值的货币表现②是货币在执行价值尺度的职能③不具有一般等价物的职能④是货币在执行流通手段的职能A.①④B.①②C.②③D.①③7.2019年8月我国央行相关负责人表示,我国未来推出的数字货币将是对流通现金具有一定替代性的全新加密电子货币体系,可以脱离传统银行账户实现价值转移,使交易环节对账户依赖程度大为降低。
一、选择题1.“货币是价值形式发展的结果,它是在商品交换的漫长历史发展过程中从商品世界中游离出来的一种特殊商品。
货币是价值形式的完成形态,这就是货币的起源。
”下列对材料观点解读正确的有①商品一商品的快速跳跃导致了货币的出现②货币作为特殊商品在本质上充当了一般等价物③货币的产生使商品交换成为现实④货币体现了商品生产者之间的社会经济关系A.①②B.①③C.②④D.③④2.根据下图信息,可以得出的正确判断有①耕牛是斧子等物品的价格②耕牛天然具有货币的特性③耕牛充当了商品交换的媒介④耕牛充当了一般等价物A.①② B.①④ C.②③ D.③④3.在原始社会,人们使用以物易物的方式交换自己所需要的物资,比如一头牛换两把石斧。
有时候受用于交换的物资种类的限制,人们不得不寻找一种能够为交换双方接受的物品。
结合图示,下列说法正确的是()①粮食换斧子的交换难以实现②两把斧子和 20斤粮食价值相等③黄金固定充当了一般等价物④耕牛充当了商品交换的媒介A.①② B.②④ C.①③ D.③④4.央行公布2019年贵金属纪念币发行计划,共13项66个品种。
这些纪念币本质上是A.商品B.一般等价物C.价值符号D.收藏品5.电视纪录片《货币》在片头这样写道:“它在今天人们的心中,仿佛是空气、是水、是阳光,是陪伴人一生的东西…人们知道她从哪里来,但不知道她到哪里去。
她就是神奇而陌生的货币”。
货币之所以神奇,最根本的原因是A.货币能买到人们所需要的一切B.货币具有体积小、价值大、易保存特点C.货币的本质是一般等价物D.货币是商品交换发展到一定阶段的产物6.2019年华为公司推出全新HUAWEI Mate BookE二合一电脑,内置4GLTE,配置多天线接收技术,提高接收信号的能力。
市场上的HUAWEI Mate BookE二合一电脑A.是价值与使用价值的统一体B.其价格是由配置的新技术决定的C.它的本质是一般等价物D.价值和使用价值归华为公司所有7.早期充当一般等价物的商品有牲畜、布帛、贝壳、象牙等,但历史上后来选择由贵金属金银固定长期充当,这是因为()①商品交换的发展使金银成为等价物②金银的体积小,价值大③金银具有不易磨损、易分割、易保存和携带等特点④人们乐于接受金银,它是交换媒介A.①②B.③④C.①④D.②③8.货币一方面可代表已经卖掉的商品,另一方面可代表能够买到的商品。
《二元关系》部分习题参考答案
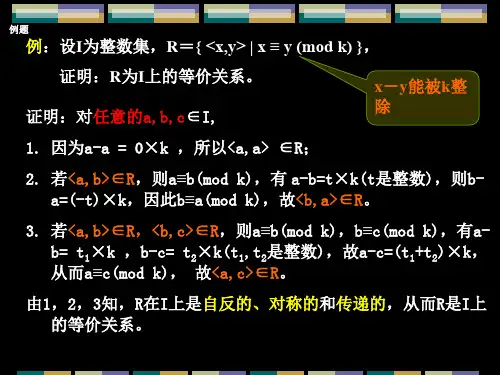
3.5 等价关系和划分(P129)
第2题
证明:∀x∈A,<x,x>∈R;∀<x,y>∈R,<y,x>∈R;∀<x,y>∈R,<y,z>∈R,则有<x,z>∈R,所以R是自反的、对称的、传递的,因而R 是等价关系。
第3题
解:(1)A上最大等价关系是全域关系,故其元素个数为n2个。
(2)A上最大等价关系的秩是1。
(3)A上最小等价关系是相等关系,故其元素个数为n个。
(4)A上最小等价关系的秩为n。
第5题
解:(a)不是等价关系。
因为A⨯A-R1不具有自反性。
(b)也不是等价关系。
也不具有自反性。
(c)是等价关系。
(d)不是等价关系。
(e)不是等价关系。
第7题
解:(a)R=“<”不是等价关系,因为<不具有自反性和对称性。
R诱导的等价关系全域关系。
(b)它不是等价关系。
因为<0,0>∉R,所以不具有自反性。
R诱导的等价关系是R⋃<0,0>。
(c)它不是等价关系。
因为<0,0>∉R,故它不具有自反性,有<0,1>∈R,但<1,0>∉R,故它不具有对称性。
R诱导的等价关系是:
{<a,b>|(a≥0∧b≥0)∨(a≤0∧b≤0)}
(d)它不是等价关系。
因为<0,0>∉R,所以不具有自反性。
(e) 它不是等价关系。
因为R不具有对称性。
R诱导的等价关系为I上的全域关系。
第10题
解:A的所有划分如下:
π1={{a,b,c}} π2={{a},{b,c}}
π3={{b},{a,c}} π4={{c},{a,b}} π5={{a},{b},{c}}
<P,细分>的哈斯图为:
第11题
解:(a) π1所诱导的等价关系的序偶为:
R1={<a,a>,<a,b>,<a,c>,<b,a>,<b,b>,<b,c>,<c,a>,<c,b>,<c,c>,<d,d>} (b) π2和π3诱导的等价关系分别是:
R2={<a,a>,<b,b>,<c,c>,<d,d>}
R3=A⨯A
(c){{ π1, π2, π3},细分}的哈斯图为:
第12题
解:(a)如果π1=π2,则π1⋃π2是A的划分,其他情况不是A的划分。
(b)如果π1=π2,则π1⋂π2是A的划分,其他情况不是A的划分。
(c) 如果π1⋂π2=∅,则π1-π2是A的划分,其他情况不是A的划分。
(d)因为[π1⋂π2-π1]⋃π1=π1,所以是A的划分。
第16题
解:(a)其哈斯图为:
(b)(A/R1)∙(A/R2)诱导的等价关系为R4:aR4b⇔a≡b(mod 15)其秩为15。
(A/R1)∙(A/R3)诱导的等价关系为R3,其秩为6。
(A/R1)+(A/R2)诱导的等价关系为I⨯I,即全域关系,其秩为1。
(A/R1)+(A/R3)诱导的等价关系为R1,其秩为3。