数字信号处理实验4-6

格式：doc
大小：253.75 KB
文档页数：25

下载文档原格式

数字信号处理第三版西科大课后答案第6章

λp=1,
s
s p
4
(4) 求阶数N和ε。
N arch k 1
arch s
k 1
100.1as 1 100.1ap 1 1456.65
N arch 1456.65 3.8659 arch 4
为了满足指标要求，取N=4。
100.1ap 1 0.2171
(3) 求归一化系统函数G(p)
3.2361p 1
或
G( p)
1
( p2 0.618 p 1)( p2 1.618 p 1)( p 1)
当然，也可以先按教材（6.2.13）式计算出极点：
p ejπ
1 2
2k 1 2N
k
k 0,1, 2,3, 4
再由教材（6.2.12）式写出G(p)表达式为
G( p) 4 1
( p pk )
p1
ch0.5580 sin
π 8
j
ch0.5580 cos
π 8
0.4438
j1.0715
3π
3π
p2 ch0.5580sin 8 j ch0.5580 cos 8 1.0715 j0.4438
p3
ch0.5580 sin
5π 8
j
ch0.5580 cos
5π 8
1.0715
j0.4438
fp=20 kHz，阻带截止频率fs=10 kHz， fp处最大衰减为3 dB，
阻带最小衰减as=15 dB。求出该高通滤波器的系统函数Ha(s)。
解: (1) 确定高通滤波器技术指标要求：
p=20 kHz, ap=3 dB fs=10 kHz, as=15 dB
(2) 求相应的归一化低通滤波器技术指标要求：套用图 5.1.5中高通到低通频率转换公式②， λp=1, λs=Ωp/Ωs，得到

数字信号处理实验离散序列的基本运算

subplot(1,2,2),stem(n1,x1,'filled','k');
title('x(-n)');
五、序列的尺度变换
n=0:40;tn=n./20;
x=sin(2*pi*tn);
x1=sin(2*pi*tn*2);
x2=sin(2*pi*tn/2);
subplot(3,1,1),stem(tn,x,'filled','k');
ylabel('δ(n-4)');
subplot(3,1,3);stem(n,x3,'filled','k');
axis([n1,n2,1.1*min(x3),1.1*max(x3)]);
ylabel('δ(n-2)+δ(n-4)');
2.n1=-4:6;n01=-2;
x1=[(n1-n01)>=0];
x=y1+y2;
subplot(3,1,1);
stem(n1,x1,'filled','k');
ylabel('x1(n)');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);
subplot(3,1,2);
stem(n2,x2,'filled','k');
ylabel('x2(n)');
axis([min(n),max(n),1.1*min(x),1.1*max(x)]);
subplot(3,1,3);
stem(n,x,'filled','k');

数字信号处理课后答案+第4章(高西全丁美玉第三版)

6*．按照下面的IDFT算法编写MATLAB语言 IFFT程序，其中的FFT部分不用写出清单，可调用fft函数。并分别对单位脉冲序列、矩形序列、三角序列和正弦序列进行 FFT和IFFT变换，验证所编程序。
解：为了使用灵活方便，将本题所给算法公式作为函数编写ifft46.m如下： %函数ifft46.m %按照所给算法公式计算IFET function xn=ifft46(Xk， N) Xk=conj(Xk)； %对Xk取复共轭 xn=conj(fft(Xk， N))/N； %按照所给算法公式计算IFFT 分别对单位脉冲序列、长度为8的矩形序列和三角序列进行FFT，并调用函数ifft46计算IFFT变换，验证函数 ifft46的程序ex406.m如下：
快速卷积时，需要计算一次N点FFT（考虑到H(k)= DFT［h(n)］已计算好存入内存）、 N次频域复数乘法和一次N点IFFT。所以，计算1024点快速卷积的计算时间Tc 约为
Fs <
1024 = 15 625 次 /秒 65536 × 10−6
Fs 15625 = = 7.8125 kHz 2 2
1 x ( n) = IDFT[ X ( k )] = [DFT[ X * ( k )]]* N
%程序ex406.m %调用fft函数计算IDFT x1n=1； %输入单位脉冲序列x1n x2n=［1 1 1 1 1 1 1 1］； %输入矩形序列向量x2n x3n=［1 2 3 4 4 3 2 1］； %输入三角序列序列向量x3n N=8； X1k=fft(x1n， N)； X2k=fft(x2n， N)； X3k=fft(x3n， N)； %计算x1n的N点DFT %计算x2n的N点DFT %计算x3n的N点DFT

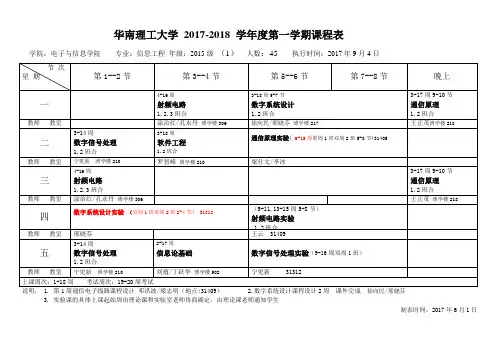
华南理工大学2017-2018学年度第一学期课程表

华南理工大学2017-2018 学年度第一学期课程表学院：电子与信息学院专业：信息工程年级：2015级（1）人数：45执行时间：2017年9月4日说明： 1.第1周通信电子线路课程设计邓洪波/梁志明（地点:31409） 2.数字系统设计课程设计2周课外完成徐向民/邢晓芬3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2017年6月1日学院：电子与信息学院专业：信息工程年级：2015级（2）人数：44执行时间：2017年9月4日说明： 1.第2周通信电子线路课程设计（地点:31409） 2.数字系统设计课程设计2周课外完成徐向民/邢晓芬3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2017年6月1日学院：电子与信息学院专业：信息工程年级：2015级（3）人数：41执行时间：2017年9月4日说明： 1.第3周通信电子线路课程设计（地点:31409） 2.数字系统设计课程设计2周课外完成姜小波3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2017年6月1日华南理工大学2017-2018 学年度第一学期课程表学院：电子与信息学院专业：信息工程年级：2015级（4）人数：37 执行时间：2017年9月4日说明：1.第4周通信电子线路课程设计（地点:31409） 2.数字系统设计课程设计2周课外完成姜小波3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2017年6月1日华南理工大学2017-2018 学年度第一学期课程表学院：电子与信息学院专业：信息工程年级：2015级（5）人数：36 执行时间：2017年9月4日说明：1.第6周通信电子线路课程设计（地点:31409） 2.数字系统设计课程设计2周课外完成王前/李韬3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2017年6月1日学院：电子与信息学院专业：信息工程年级：2015级（6）人数：30执行时间：2017年9月4日说明：1.第7周通信电子线路课程设计（地点:31409） 2.数字系统设计课程设计2周课外完成王前/李韬3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2017年6月1日.学院：电子与信息学院专业：信息工程（冯秉铨实验班）年级：2015级人数：①52执行时间：2017年9月4日说明：1.第8周通信电子线路课程设计（地点:31409） 2.数字系统设计课程设计2周课外完成李磊3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生4.射频电路实验如选修人数超过78人，超出的同学需由任课老师另外安排一次上课时间制表时间：2017年6月1日华南理工大学2017-2018 学年度第一学期课程表学院：电子与信息学院专业：电子科学与技术（卓越班）年级：2015级人数：27执行时间：2017年9月4日说明：1. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2015年6月华南理工大学2017-2018 学年度第一学期课程表学院：电子与信息学院专业：电子科学与技术（1）年级：2015级人数：53执行时间：2017年9月4日说明： 1. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生2.射频电路实验如选修人数超过78人，超出的同学需由任课老师另外安排一次上课时间制表时间：2017年6月1日。

实验六用窗函数法设计FIR滤波器分析解析

实验六用窗函数法设计FIR滤波器分析解析一、引言数字滤波器是数字信号处理中的重要组成部分。

滤波器可以用于去除噪声、调整频率响应以及提取感兴趣的信号。

有许多方法可以设计数字滤波器，包括窗函数法、频域法和优化法等。

本实验将重点介绍窗函数法设计FIR滤波器的原理和过程。

二、窗函数法设计FIR滤波器窗函数法是设计FIR滤波器的一种常用方法。

其基本原理是将滤波器的频率响应与理想滤波器的频率响应进行乘积。

理想滤波器的频率响应通常为矩形函数，而窗函数则用于提取有限长度的理想滤波器的频率响应。

窗函数的选择在FIR滤波器的设计中起着重要的作用。

常用的窗函数包括矩形窗、汉宁窗、汉明窗、布莱克曼窗等。

对于每种窗函数，都有不同的特性和性能指标，如主瓣宽度、副瓣抑制比等。

根据不同的应用需求，可以选择合适的窗函数。

窗函数法设计FIR滤波器的具体步骤如下：1.确定滤波器的阶数N。

阶数N决定了滤波器的复杂度，一般情况下，阶数越低，滤波器的简单度越高，但频率响应的近似程度也会降低。

2.确定滤波器的截止频率。

根据应用需求，确定滤波器的截止频率，并选择合适的窗函数。

3.根据窗函数长度和截止频率计算理想滤波器的频率响应。

根据所选窗函数的特性，计算理想滤波器的频率响应。

4.根据理想滤波器的频率响应和窗函数的频率响应，得到所需的FIR滤波器的频率响应。

将理想滤波器的频率响应与窗函数的频率响应进行乘积，即可得到所需滤波器的频率响应。

5.对所得到的频率响应进行逆傅里叶变换，得到时域的滤波器系数。

6.实现滤波器。

利用所得到的滤波器系数，可以通过卷积运算实现滤波器。

三、实验结果与分析本实验以Matlab软件为平台，利用窗函数法设计了一个低通滤波器。

滤波器的阶数为16，截止频率为500Hz，采样频率为1000Hz，选择了汉宁窗。

根据上述步骤，计算得到了所需的滤波器的频率响应和时域的滤波器系数。

利用这些系数，通过卷积运算，实现了滤波器。

为了验证滤波器的性能，将滤波器应用于输入信号，观察输出信号的变化。

《数字信号处理》课后答案

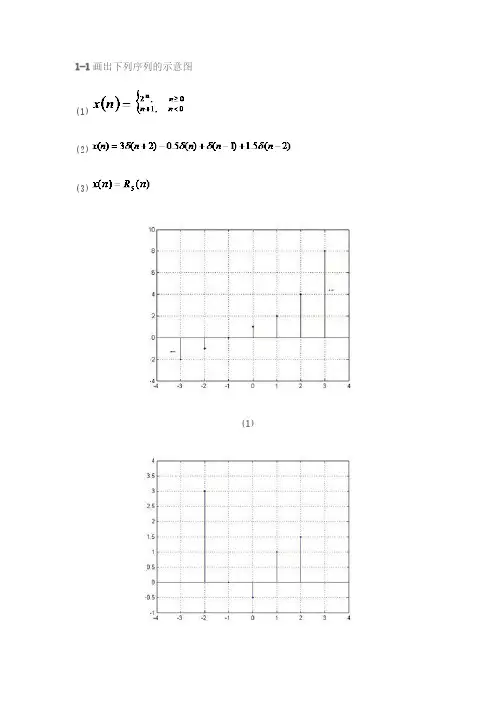
数字信号处理课后答案 1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。

解：()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号：25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它（1）画出()x n 序列的波形，标上各序列的值；（2）试用延迟单位脉冲序列及其加权和表示()x n 序列；（3）令1()2(2)x n x n =-，试画出1()x n 波形；（4）令2()2(2)x n x n =+，试画出2()x n 波形；（5）令3()2(2)x n x n =-，试画出3()x n 波形。

解：（1）x(n)的波形如题2解图（一）所示。

（2）()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-（3）1()x n 的波形是x(n)的波形右移2位，在乘以2，画出图形如题2解图（二）所示。

（4）2()x n 的波形是x(n)的波形左移2位，在乘以2，画出图形如题2解图（三）所示。

（5）画3()x n 时，先画x(-n)的波形，然后再右移2位，3()x n 波形如题2解图（四）所示。

3. 判断下面的序列是否是周期的，若是周期的，确定其周期。

（1）3()cos()78x n A n ππ=-，A 是常数；（2）1()8()j n x n e π-=。

解：（1）3214,73w w ππ==，这是有理数，因此是周期序列，周期是T=14；（2）12,168w wππ==，这是无理数，因此是非周期序列。

5. 设系统分别用下面的差分方程描述，()x n 与()y n 分别表示系统输入和输出，判断系统是否是线性非时变的。

数字信号处理(Digital Signal Processing)智慧树知到课后章节答案2023年

数字信号处理（Digital Signal Processing）智慧树知到课后章节答案2023年下聊城大学聊城大学绪论单元测试1.声音、图像信号都是（）。

A:二维信号 B:一维信号 C:确定信号 D:随机信号答案:随机信号第一章测试1.序列的周期为（）。

A:7 B:7 C:14 D:14答案:142.序列的周期为（）。

A:10 B:10 C:8 D:8答案:103.对于一个系统而言，如果对于任意时刻n0，系统在该时刻的响应仅取决于此时刻及此时刻以前时刻的输入系统，则称该系统为____系统。

（）A:线性 B:因果 C:稳定 D:非线性答案:因果4.线性移不变系统是因果系统的充分必要条件是______。

（）A:n<0,h(n)=0 B:n>0,h(n)=0 C:n>0,h(n)>0 D:n<0,h(n)>0答案:n<0,h(n)=05.要想抽样后能够不失真的还原出原信号，则抽样频率必须，这就是奈奎斯特抽样定理。

（）A:等于2倍fm B:小于等于2倍fm C:大于2倍fm D:大于等于2倍fm答案:大于等于2倍fm6.已知x(n)=δ(n),其N点的DFT[x(n)]=X(k),则X(N-1)= 1。

（）A:对 B:错答案:对7.相同的Z变换表达式一定对应相同的时间序列。

（）A:对 B:错答案:错8.滤波器设计本质上是用一个关于z的有理函数在单位圆上的特性来逼近所有要求的系统频率特性。

（）A:错 B:对答案:对9.下面描述中最适合离散傅立叶变换DFT的是（）A:时域为离散周期序列，频域也为离散周期序列 B:时域为离散有限长序列，频域也为离散有限长序列 C:时域为离散序列，频域也为离散序列 D:时域为离散无限长序列，频域为连续周期信号答案:时域为离散有限长序列，频域也为离散有限长序列10.巴特沃思滤波器的幅度特性必在一个频带中（通带或阻带）具有等波纹特性。

（）A:错 B:对答案:错第二章测试1.N＝1024点的DFT，需要复数相乘次数约（）。

数字信号处理(西电上机实验)

数字信号处理实验报告实验一：信号、系统及系统响应一、实验目的：(1) 熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解。

(2) 熟悉时域离散系统的时域特性。

(3) 利用卷积方法观察分析系统的时域特性。

(4) 掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。

二、实验原理与方法：(1) 时域采样。

(2) LTI系统的输入输出关系。

三、实验内容、步骤(1) 认真复习采样理论、离散信号与系统、线性卷积、序列的傅里叶变换及性质等有关内容，阅读本实验原理与方法。

(2) 编制实验用主程序及相应子程序。

①信号产生子程序，用于产生实验中要用到的下列信号序列：a. xa(t)=A*e^-at *sin(Ω0t)u(t)A=444.128;a=50*sqrt(2)*pi;b. 单位脉冲序列：xb(n)=δ(n)c. 矩形序列：xc(n)=RN(n), N=10②系统单位脉冲响应序列产生子程序。

本实验要用到两种FIR系统。

a. ha(n)=R10(n);b. hb(n)=δ(n)+2.5δ(n-1)+2.5δ(n-2)+δ(n-3)③有限长序列线性卷积子程序用于完成两个给定长度的序列的卷积。

可以直接调用MATLAB语言中的卷积函数conv。

conv用于两个有限长度序列的卷积，它假定两个序列都从n=0 开始。

调用格式如下：y=conv (x, h)四、实验内容调通并运行实验程序，完成下述实验内容：①分析采样序列的特性。

a. 取采样频率fs=1 kHz, 即T=1 ms。

b. 改变采样频率，fs=300 Hz，观察|X(ejω)|的变化，并做记录(打印曲线)；进一步降低采样频率，fs=200 Hz，观察频谱混叠是否明显存在，说明原因，并记录(打印)这时的|X(ejω)|曲线。

②时域离散信号、系统和系统响应分析。

a. 观察信号xb(n)和系统hb(n)的时域和频域特性；利用线性卷积求信号xb(n)通过系统hb(n)的响应y(n)，比较所求响应y(n)和hb(n)的时域及频域特性，注意它们之间有无差别，绘图说明，并用所学理论解释所得结果。

数字信号处理实验指导书

注意此书用的时候N要先付值数字信号处理实验指导书目录前言 (1)第一章MATLAB基础知识 (1)第二章MATLAB基本数值运算 (4)第三章MATLAB的图形处理功能 (8)第四章MATLAB的程序设计 (11)第五章常用数字信号处理函数 (16)第六章MATLAB在数字信号处理中的应用 (23)实验一常见离散信号的MATLAB产生和图形显示 (33)实验二离散系统的频率响应分析和零、极点分布 (37)实验三序列线性卷积、圆周卷积的计算及其关系的研究 (39)实验四利用DFT分析信号的频谱 (41)实验五信号时间尺度变换的研究 (43)实验六快速傅里叶变换及其应用 (47)实验七IIR滤波器的实现与应用 (56)实验八FIR滤波器的实现与应用 (61)第一章MATLAB基础知识§1-1 MA TLAB软件简介MATLAB，Matrix Laboratory的缩写，是由Mathworks公司开发的一套用于科学工程计算的可视化高性能语言，具有强大的矩阵运算能力。

它集数值分析、矩阵运算、信号处理和图形显示于一体，构成了一个界面友好的用户环境，在这个环境中，问题与求解都能方便地以数学的语言（主要是矩阵形式）或图形方式表示出来。

与大家常用的Fortran 和C等高级语言相比，MA TLAB的语法规则更简单，更贴近人的思维方式，被称为“草稿纸式的语言”。

§1-2 MA TLAB应用入门1．MATLAB的安装与卸载MATLAB软件在用户接口时具有较强的亲和力，其安装过程比较典型，直接运行光盘中的安装向导支撑程序SETUP.exe，按其提示一步步选择即可。

MATLAB自身带有卸载程序，在其安装目录下有uninstall子目录，运行该目录下uninstall.exe的即可；也可以通过Windows系统的安装卸载程序进行卸载。

2．MATLAB的启动与退出MATLAB安装完成后，会自动在Windows桌面上生成一个MA TLAB图标，它是指向安装目录下\bin\win32\matlab.exe的链接，双击这个图标即可来到MATLAB集成环境的基本窗口；也可以在开始菜单的程序选项中选择MATLAB 快捷方式；还可以在MA TLAB的安装路径的bin子目录中双击可执行文件matlab.exe。

数字信号处理课后习题答案

（修正：此题有错，
(3)系统的单位脉冲响应而改变，是两个复序列信号之和）
(4)
（修正：随上小题答案
（修正：此图错误，乘系数应该为 0.5，输出端 y(n)应该在两个延迟器 D 之间）
1-25 线性移不变离散时间系统的差分方程为
(1)求系统函数； (2)画出系统的一种模拟框图； (3)求使系统稳定的 A 的取值范围。解：(1)
(2)
(3)
解：（1）
（2）
（3）
1-7 若采样信号 m(t)的采样频率 fs=1500Hz，下列信号经 m(t)采样后哪些信号不失真？ (1) (2) (3) 解：
(1)
采样不失真
(2)
采样不失真
(3)
，
采样失真
1-8 已知
,采样信号的采样周期为。
(1) 的截止模拟角频率是多少？
(2)将进行 A/D 采样后，如何？
（3）最小阻带衰减 5-4
由分式（5.39）根据 A 计算，如下：由表 5.1 根据过度带宽度计算窗口：
单位脉冲响应如下：
单位脉冲响应如下：
其中为凯泽窗。 5-5 答：减小窗口的长度 N，则滤波器的过度带增加，但最小阻带衰减保持不变。 5-6：图 5.30 中的滤波器包括了三类理想滤波器，包括了低通，带通和高通，其响应的单位
(1)
，
(2)
1-18 若当时
；时
(1)
，其中
(2) 证明：
，收敛域
,其中 N 为整数。试证明：，
(1) 令其中
，则 ,
(2)
,
1-19 一系统的系统方程及初时条件分别如下：，
(1)试求零输入响应，零状态响应，全响应； (2)画出系统的模拟框图解： (1)零输入响应

4-6-POP的贴装与返修技术介绍

PoP器件的外形封装结构（举例）
底面
顶面(有Mark)
• JEDEC JC-11对PoP设计和机械结构的标准化以及 JEDEC JC-63对顶层存储器件引脚输出的标准化工作正在进行中
PCB焊盘设计（举例） Univos (Universal) demo PCB
SMD与NSMD焊盘设计
SMD
• 回流后，顶部器件底面和底部元件顶面的间隙f2
Assembly x-ray
• Bottom component placement accuracy is very good.
• Bottom component placement accuracy iCSP
4-6- 元件堆叠装配（PoP ，Package on Package）的贴装与返修技术介绍
顾霭云
• 随着移动多媒体产品的普及和对更高数字信号处理、具有更高存储容量和灵活性的需求，元件堆叠装配(PoP,
Package on Package)技术的应用正在快速增长。
• 在集成复杂逻辑和存储器件方面，PoP是一种新兴的、成本最低的3D封装解决方案。通过堆叠实现小型化、多功能。
合格焊点
不合格焊点
不合格焊点
⑥ 可靠性(是否需要底部填充underfill)
• 目前大多采用underfill来解决可靠性问题，但是pop的
underfill的难度可比一般的BGA/CSP的难度要高很多，因
为有两个以上层面需要进行点胶，而且还要保证每层都能均匀的布满，是个难题。 • 胶水选择和填充工艺的合理安排很关键。
6. 回流焊接及检测
⑴ PoP面堆叠贴片（装配）工艺
• 以三层堆叠的ASIC+存储器为例：

数字信号处理MATLAB实验

出该信号，并讨论信号的混叠情况。
（3）令
,其中 f/fs=1/16，即每个周期有 16 个
点。试利用 MATLAB 编程实现：
○1 作 M=4 倍的抽取，使每个周期变成 4 点。
○2 作 L=3 倍的插值，使每个周期变成 48 点。
（4）输入信号 x（n）为归一化频率分别为 f1=0.04，f2=0.3 的正弦信号相加而成，N=50，插因子为 5，抽取因子为 3，给出按有理因子 5/3 做采样率变换的输入输出波形。
(8) 用 FFT 分别计算 xa (n)( p 8, q 2) 和 xb(n) (a=0.1,f=0.0625)的自相关函数。
三、思考题
(1)实验中的信号序列 xc(n)和 xd(n)，在单位圆上的 z 变换频谱
和一些，为什么？
会相同吗？如果不同，说明哪一个低频分量更多
(2)对一个有限长序列进行 DFT 等价于将该序列周期延拓后进行
0≤n≤15
c）x(n)=3cos(0.125πn+0.2π)+2sin(0.25πn+0.1π) 0≤n≤15 d）将c)中的x(n)扩展为以16为周期的函数x16(n)=x(n+16),绘出四个周期。 e）将c)中的x(n)扩展为以10为周期的函数x10(n)=x(n+10),绘出四个周期。 (3)x(n)=[1,-1,3,5]，产生并绘出下列序列的样本。
(6)产生一 512 点的随机序列 xe(n)，并用 xc(n)和 xe(n)做线性卷积，观察卷积前后 xe(n)频谱的变化。要求将 xe(n)分成 8 段，分别采用重叠相加法和重叠保留法。
(7) 用 FFT 分别计算 xa (n)( p 8, q 2) 和 xb(n) (a=0.1,f=0.0625)的 16 点循环相关和线性相关，问一共有多少种结果，他们之间有何异同点。

《数字信号处理实验》指导书

《数字信号处理实验》实验1 常用信号产生实验目的：学习用MATLAB编程产生各种常见信号。

实验内容：1、矩阵操作：输入矩阵：x=[1 2 3 4;5 4 3 2;3 4 5 6;7 6 5 4]引用 x的第二、三行；引用 x的第三、四列；求矩阵的转置；求矩阵的逆；2、单位脉冲序列：产生δ（n）函数；产生δ（n-3）函数；3、产生阶跃序列：产生U（n）序列；产生U（n-n0）序列；4、产生指数序列：x(n)=0.5n⎪⎭⎫⎝⎛4 35、产生正弦序列：x=2sin(2π*50/12+π/6)6、产生取样函数：7、产生白噪声：产生[0，1]上均匀分布的随机信号：产生均值为0，方差为1的高斯随机信号：8、生成一个幅度按指数衰减的正弦信号：x(t)=Asin(w0t+phi).*exp(-a*t)9、产生三角波：实验要求：打印出程序、图形及运行结果，并分析实验结果。

实验2 利用MATLAB 进行信号分析实验目的：学习用MATLAB 编程进行信号分析实验内容：1数字滤波器的频率响应：数字滤波器的系统函数为：H(z)=21214.013.02.0----++++z z z z ，求其幅频特性和相频特性：2、离散系统零极点图：b =[0.2 0.1 0.3 0.1 0.2];a=[1.0 -1.1 1.5 -0.7 0.3];画出其零极点图3、数字滤波器的冲激响应：b=[0.2 0.1 0.3 0.1 0.2];a=[1.0 -1.1 1.5 -0.7 0.3];求滤波器的冲激响应。

4、计算离散卷积：x=[1 1 1 1 0 0];y=[2 2 3 4];求x(n)*y(n)。

5、系统函数转换：（1）将H(z)=)5)(2)(3.0()1)(5.0)(1.0(------z z z z z z 转换为直接型结构。

（2）将H （z ）=3213210.31.123.7105.065.06.11-------+--+-zz z z z z 转换为级联型结构。

实验六数字信号处理在双音多频拨号系统中的应用

for q=1:4;if tm(p,q)==abs(d); break,end % 检测码相符的列号q endif tm(p,q)==abs(d); break,end % 检测码相符的行号pendn=0:1023; % 为了发声，加长序列x = sin(2*pi*n*f1(p)/8000) + sin(2*pi*n*f2(q)/8000);% 构成双频信号sound(x,8000); % 发出声音pause(0.1)% 接收检测端的程序X=goertzel(x(1:205),K+1); % 用Goertzel算法计算八点DFT样本val = abs(X); % 列出八点DFT向量subplot(3,2,l);stem(K,val,'.');grid;xlabel('k');ylabel('|X(k)|') % 画出DFT(k)幅度axis([10 50 0 120])limit = 80; %for s=5:8;if val(s) > limit, break, end % 查找列号endfor r=1:4;if val(r) > limit, break, end % 查找行号endTNr=TNr+tm(r,s-4)*10^(6-l);enddisp('接收端检测到的号码为：') % 显示接收到的字符disp(TNr)分析：运行程序，根据提示键入6位电话号码678012，回车后可以听见6位电话号码对应的DTMF 信号的声音，并输出相应的6幅频谱图如图1所示，左上角的第一个图在k=20和k=38两点出现峰值，所以对应第一位号码数字6。

最后显示检测到的电话号码678012。

（2）分析该仿真程序，将产生、检测和识别6位电话号码的程序改为能产生、检测和识别8位电话号码的程序，并运行一次，打印出相应的幅度谱和8位电话号码。

实验代码：8位号码% DTMF双频拨号信号的生成和检测程序%clear all;clc;tm=[1,2,3,65;4,5,6,66;7,8,9,67;42,0,35,68]; % DTMF信号代表的16个数N=205;K=[18,20,22,24,31,34,38,42];f1=[697,770,852,941]; % 行频率向量f2=[1209,1336,1477,1633]; % 列频率向量TN=input('键入8位电话号码= '); % 输入8位数字TNr=0; %接收端电话号码初值为零for l=1:8;d=fix(TN/10^(8-l));TN=TN-d*10^(8-l);分析：运行程序，根据提示键入8位电话号码45678012，回车后可以听见8位电话号码对应的DTMF信号的声音，并输出相应的8幅频谱图如图所示，左上角的第一个图在k=20和k=31两点出现峰值，所以对应第一位号码数字4。

华南理工大学2019-2020学年度第一学期课程表

华南理工大学2019-2020学年度第一学期课程表学院：电子与信息学院专业：信息工程年级：2017级（1）人数：41执行时间：2019年8月26日说明： 1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409） 2.数字系统设计课程设计2周课外完成王前/李韬 3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2019年6月1日华南理工大学2019-2020学年度第一学期课程表学院：电子与信息学院专业：信息工程年级：2017级（2）人数：36执行时间：2019年8月26日说明： 1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409） 2.数字系统设计课程设计2周课外完成王前/李韬 3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2019年6月1日学院：电子与信息学院专业：信息工程年级：2017级（3）人数：39执行时间：2019年8月26日说明： 1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409） 2.数字系统设计课程设计2周课外完成徐向民/邢晓芬 3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2019年6月1日学院：电子与信息学院专业：信息工程年级：2017级（4）人数：38执行时间：2019年8月26日1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409）2.数字系统设计课程设计2周课外完成徐向民/邢晓芬3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2019年6月1日学院：电子与信息学院专业：信息工程年级：2017级（5）人数：45 执行时间：2019年8月26日说明： 1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409） 2.数字系统设计课程设计2周课外完成姜小波 3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生制表时间：2019年6月1日学院：电子与信息学院专业：信息工程年级：2017级（6）人数：31执行时间：2019年8月26日说明： 1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409） 2.数字系统设计课程设计2周课外完成姜小波 3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生学院：电子与信息学院专业：信息工程（冯秉铨实验班）年级：2017级人数：①44执行时间：2019年8月26日说明： 1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409） 2.数字系统设计课程设计2周课外完成青春美 3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生华南理工大学2019-2020学年度第一学期课程表学院：电子与信息学院专业：电子科学与技术（卓越班）年级：2017级人数：26执行时间：2019年8月26日说明： 1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409） 3. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生学院：电子与信息学院专业：电子科学与技术（1）年级：2017级人数：52执行时间：2019年8月26日1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409）2. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生学院：电子与信息学院专业：电子科学与技术（2）年级：2017级人数：46执行时间：2019年8月26日1.通信电子线路课程设计停课1周，其中信工1班第1周,信工2班和电卓班第2周信工3班第3周，信工4班和6班第4周，信工5班第5周，冯班第7周，电科1班第8周、电科2班第9周，邓洪波/梁志明（地点:31409）2. 实验课的具体上课起始周由理论课和实验室老师协商确定，由理论课老师通知学生。

数字信号处理实验MATLAB上机DOC

班级：学号：姓名：日期：实验一：离散时间信号的分析一、实验目的利用DFT 卷积实现系统的时域分析二、实验原理在离散时间、连续频率的傅里叶变换中，由于卷积性质知道，对系统输出的计算可以通过求x[n]和h[n]的DTFT ，将得到的X(e jw )和H(e jw )相乘就可以得到Y(e jw )，进而再通过反变换得到y[n]。

这就避免了在时域进行繁琐的卷积求解。

三、实验步骤（包括代码和波形）1-2（2）x[k]=g[k]=k+1,0<=k<=3;x[k]=g[k]=0,其他编码如下：ak=1:4 gk=1:4Z=conv(ak,gk) stem(Z)波形如下：12345675101520251-3（1）已知序列x[k]={1,2,3,4;k=0,1,2,3},y[k]={-1,1,2,3;k=0,1,2,3},试计算x[k]的自相关函数以及序列x[k]与y[k]的互相关函数。

编码如下：x=[1,2,3,4];kx=0:3; y=[-1,1,-2,3];ky=0:3; xf=fliplr(x); s1=conv(x,xf); s2=conv(xf,y); yf=fliplr(y); s3=conv(yf,x);k1=kx(1)+ky(1):kx(end)+ky(end); kxf=-fliplr(kx);k2=kxf(1)+ky(1):kxf(end)+ky(end); kyf=-fliplr(ky);k3=kyf(1)+kx(1):kyf(end)+kx(end); subplot(2,2,1); stem(k1,s1);xlabel('k1');ylabel('s1'); subplot(2,2,2); stem(k2,s2);xlabel('k2');ylabel('s2'); subplot(2,2,3) stem(k3,s3);xlabel('k3');ylabel('s3');波形如下：0246102030k1s 1-4-2024-10-50510k2s 2-4-2024-10-50510k3s 3M-1已知g1[t]=cos(6*pi*t),g2=cos(14*pi*t),g3=cos(26*pi*t),以抽样频率f(max)=10HZ对上述三个信号进行抽样。

数字信号处理实验(吴镇扬)答案4

实验四有限长单位脉冲响应滤波器设计朱方方 03 通信四班(1) 设计一个线性相位FIR 高通滤波器，通带边界频率为π，阻带边界频率为π，阻带衰减不小于40dB 。

要求给出h(n)的解析式，并用MATLAB 绘出时域波形和幅频特性。

解：(1)求数字边界频率:0.6 , 0.4c r ωπωπ== (2)求理想滤波器的边界频率:0.5n ωπ=(3)求理想单位脉冲响应:[]d sin ()sin[()]()()1n n n n n n h n n παωααπαωαπ⎧---≠⎪⎪-=⎨⎪-=⎪⎩(4) 选择窗函数。

阻带最小衰减为-40dB ，因此选择海明窗(其阻带最小衰减为-44dB)；滤波器的过渡带宽为ππ=π，因此6.210.231 , 152N N N ππα-=⇒=== (5) 求FIR 滤波器的单位脉冲响应h(n):[]31d sin (15)sin[0.5(15)]1cos ()15()()()15(15)115n n n R n n h n w n h n n n ππππ⎧---⎡⎤⎛⎫-⋅⋅≠⎪ ⎪⎢⎥==-⎝⎭⎨⎣⎦⎪=⎩程序：clear;N=31; n=0:N-1;hd=(sin(pi*(n-15))-sin*pi*(n-15)))./(pi*(n-15)); hd(16)=; win=hanning(N); h=win'.*hd;figure; stem(n,h);xlabel('n'); ylabel('h(n)'); grid;title('FIR 高通滤波单位脉冲响应h(n)'); [H,w]=freqz(h,1); H=20*log10(abs(H)); figure;3plot(w/pi,H);axis([0 1 -100 10]);xlabel('\omega/\pi'); ylabel('幅度/dB');grid;title('FIR 高通滤波器，hanning 窗，N=31');51015202530nh (n )FIR 高通滤波器的单位脉冲响应h(n)0.10.20.30.40.50.60.70.80.91-100-90-80-70-60-50-40-30-20-10010ω/π幅度/d BFIR 高通滤波器，hanning 窗，N=31分析：由图知阻带衰减最小值大于40，满足要求。

数字信号处理课后习题答案-第六章习题与答案

1．、2．用冲激响应不变法将以下 )(s H a变换为变换为 )(z H ，抽样周期为T 。

为任意正整数 ,)()( )2()()()1(022n s s As H b a s as s H na a -=+++=分析：①冲激响应不变法满足)()()(nT h t h n h a nTt a===，T 为抽样间隔。

这种变换法必须)(s H a 先用部分分式展开。

②第（②第（22）小题要复习拉普拉斯变换公式1!][+=n n S n t L ,na n t s a S S As H t u n t Ae t h )()()()!1()(010-=⇔-=-，可求出可求出 )()()(kT Th t Th k h a kTt a===，|又 dz z dX z k kx )()(-⇔，则可递推求解。

解: (1)22111()()2a s a H s s a b s a jb s a jb ⎡⎤+==+⎢⎥+++++-⎣⎦[])( 21)()()(t u e e t h tjb a t jb a a --+-+= 由冲激响应不变法可得：由冲激响应不变法可得：由冲激响应不变法可得：[]()()()() ()2a jb nT a jb nT a T h n Th nT e e u n -+--==+ 11011() () 211naT jbT aT jbT n T H z h n z e e z e e z ∞------=⎡⎤==+⎢⎥--⎣⎦∑ 2211cos 21cos 1 ------+--⋅=z e bT z e bT z e T aT aT aT(2) 先引用拉氏变换的结论[]1!+=n n s n t L 可得：可得： n a s s As H )()(0-=))()!1()(10t u n t Ae t h n t s a -=-则 )()!1()()()(10k u n kT Ae T Tk Th k h n kT s a -⋅==- dzz dX zk kx az k u a ZZk )()( , 11)( 1-−→←-−→←-且按)11()()!1( )()!1( )()(111111000--∞=---∞=----=-==∑∑ze dz d z n AT e z k n T TA z k h z H T s n n kkT s n n k k可得⎪⎪⎩⎪⎪⎨⎧=-=-=•••---,3,2)1(1,1)(111000n z e z e AT n z e ATz H n T s T S n T s ，可以递推求得：2. 已知模拟二阶巴特沃思低通滤波器的归一化系统函数为：2'4142136.111)(s s s H a ++=而而3dB 截止频率为50Hz 的模拟滤波器，需将归一化的)('s H a 中的s 变量用502⨯πs 来代替424'108696044.928830.444108696044.9)100()(⨯++⨯==s s s H s H a a π：设系统抽样频率为设系统抽样频率为Hz f s 500=，要求从这一低通模拟滤波器设计一个低通数字滤波器，采用阶跃响应不变法。

数字信号处理第4章部分习题详解

其中 ni 、 k i 都是二进制数。
)( 2 k1 k0 ) n1k0 ( 2 n 2 n3 级间旋转因子 W16 。 W16
4
22 n1 2n2 n3 23 n0
0000 1000 0100 1100 0010 1010 0110 1110 0001 1001 0101 1101 0011 1011 0111 1111 x(0) x(8) x(4) -j x(12) x(2) x(10) x(6) -j x(14) x(1) x(9) x(5) -j x(13) x(3) x(11) x(7) x(15) -j -1 -1 -1 -1 -1 -1 -1 -1
nk X (k ) x(n)WN n 0 N 1

1
1
n3 0 n2 0 1
x(n n n n )W
n1 0 1 n0 0 1 0 1 2 3 0 1 2 3
1
1
1
( 23 n0 2 2 n1 2 n2 n3 )( 23 k3 2 2 k 2 2 k1 k0 ) 16
3
n1 0

3
3 n1 ( 4 k1 k 0 ) x(n0 n1 )W4n0 k 0 W16 n 0 0
n1k0 X 1 (n1k0 ) W16 W4n1k1 X 2 (k1k0 ) n1 0
n1 k 0 其中 W16 是级间旋转因子。

n3 0 n 2 0 1 1

n1 0
1 n3 ( 2 2 k 2 2 k1 k 0 ) x(n0n1n2n3 )W2n0 k 0 W4n1k 0 W2n1k1 W8n2 ( 2 k1 k 0 ) W2n2 k 2 W16 W2n3 k3 n 0 0

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

实验4 离散系统的变换域分析一、实验目的1、熟悉对离散系统的频率响应分析方法；2、加深对零、极点分布的概念理解。

二、实验原理离散系统的时域方程为其变换域分析方法如下：频域:系统的频率响应为:Z域:系统的转移函数为:分解因式:，其中和称为零、极点。

三、预习要求1.在MATLAB中，熟悉函数tf2zp、zplane、freqz、residuez、zp2sos的使用，其中：[z，p，K]=tf2zp（num，den）求得有理分式形式的系统转移函数的零、极点；zplane（z，p）绘制零、极点分布图；h=freqz(num,den,w)求系统的单位频率响应；[r，p，k]=residuez （num，den）完成部分分式展开计算；sos=zp2sos（z，p，K）完成将高阶系统分解为2阶系统的串联。

2.阅读扩展练习中的实例，学习频率分析法在MATLAB中的实现；3.编程实现系统参数输入，绘出幅度频率响应和相位响应曲线和零、极点分布图。

四、实验内容求系统的零、极点和幅度频率响应和相位响应。

解析：【代码】num=[0.0528 0.0797 0.1295 0.1295 0.797 0.0528];den=[1 -1.8107 2.4947 -1.8801 0.9537 -0.2336];[z,p,k]=tf2zp(num,den);disp('零点');disp(z);disp('极点');disp(p);disp('增益系数');disp(k);figure(1)zplane(num,den)figure(2)freqz(num,den,128)【图形】-2-1.5-1-0.500.511.5-1.5-1-0.50.511.5Real PartI m a g i n a r y P a r t0.10.20.30.40.50.60.70.80.91-800-600-400-2000Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s)0.10.20.30.40.50.60.70.80.91-40-2002040Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )【结果】零点-1.5870 + 1.4470i-1.5870 - 1.4470i0.8657 + 1.5779i0.8657 - 1.5779i-0.0669 + 0.0000i极点0.2788 + 0.8973i0.2788 - 0.8973i0.3811 + 0.6274i0.3811 - 0.6274i0.4910 + 0.0000i增益系数0.0528五、扩展练习例1: 求下列直接型系统函数的零、极点，并将它转换成二阶节形式解:用MATLAB计算程序如下：num=[1 -0.1 -0.3 -0.3 -0.2];den=[1 0.1 0.2 0.2 0.5];[z,p,k]=tf2zp(num,den);m=abs(p);disp('零点');disp(z);disp('极点');disp(p);disp('增益系数');disp(k);sos=zp2sos(z,p,k);disp('二阶节');disp(real(sos));zplane(num,den)输入到“num”和“den”的分别为分子和分母多项式的系数。

计算求得零、极点增益系数和二阶节的系数：零点:0.9615-0.5730-0.1443 + 0.5850i-0.1443 - 0.5850i极点:0.5276+0.6997i0.5276-0.6997i-0.5776+0.5635i-0.5776-0.5635i增益系数:1二阶节:1.0000 -0.3885 -0.5509 1.0000 1.15520 0.65111.0000 0.28850 0.36300 1.0000 -1.0552 0.7679系统函数的二阶节形式为：极点图见图:-1-0.500.51-1-0.8-0.6-0.4-0.200.20.40.60.81Real PartI m a g i n a r y P a r t图系统函数的零、极点图例2: 差分方程所对应的系统的频率响应。

解:差分方程所对应的系统函数为：用MATLAB 计算的程序如下： k=256;num=[0.8 -0.44 0.36 0.02]; den=[1 0.7 -0.45 -0.6]; w=0:pi/k:pi; h=freqz(num,den,w); subplot(2,2,1);plot(w/pi,real(h));gridtitle('实部')xlabel('\omega/\pi');ylabel('幅度') subplot(2,2,2);plot(w/pi,imag(h));grid title('虚部')xlabel('\omega/\pi');ylabel('Amplitude') subplot(2,2,3); plot(w/pi,abs(h));grid title('幅度谱')xlabel('\omega/\pi');ylabel('幅值') subplot(2,2,4);plot(w/pi,angle(h));grid title('相位谱')xlabel('\omega/\pi');ylabel('弧度')0.51-20246实部ω/π幅度0.51-20246虚部ω/πA m p l i t u d e0.5102468幅度谱ω/π幅值0.51-10123相位谱ω/π弧度图实验5 有限冲激响应数字滤波器设计一、实验目的：1、加深对数字滤波器的常用指标理解。

2、学习数字滤波器的设计方法。

二、实验原理：低通滤波器的常用指标：（1）通带边缘频率；（2）阻带边缘频率；（3）通带起伏；（4）通带峰值起伏，（5）阻带起伏，最小阻带衰减。

三、预习要求1. 在MATLAB 中，熟悉函数fir1、kaiserord 、remezord 、remez 的使用；B = fir1(n,Wn,'high','noscale')设计滤波器；[n,Wn,beta,ftype] = kaiserord(f,a,dev)估计滤波器阶数；[n,fo,ao,w] = remezord (f,a,dev,fs)计算等波纹滤波器阶数n 和加权函数w(ω)； B=remez(n,f,a)进行等波纹滤波器的设计。

2. 阅读扩展练习中的实例，学习FIR 滤波器的设计方法及其在MATLAB 中的实现；3. 给出FIR 数字滤波器的冲激响应，绘出它们的幅度和相位频响曲线，讨论它们各自的实现形式和特点。

数字滤波器有IIR 和FIR 两种类型，它们的特点和设计方法不同。

四、实验内容：利用MATLAB 编程,分别用窗函数法和等波纹滤波器法设计两种FIR 数字滤波器，指标要求如下：通带边缘频率：，通带峰值起伏：。

阻带边缘频率：，最小阻带衰减：。

用窗函数法设计：【解析】调用函数[n,wn,bta,ftype]=kaiserord （f ，a ，dev ，fs ）参数：f=[0.3 0.45 0.65 0.8]为对应数字频率a=[0 1 0]为由f 指定的各个频带上的幅值向量，一般只有0和1表示；和f 长度关系为（2*a 的长度）—2=（f 的长度）devs=[0.01 0.1087 0.01]用于指定各个频带输出滤波器的频率响应与其期望幅值之间的最大输出误差或偏差，长度与a 相等，计算公式：阻带衰减误差=20s 10sαδ-=，通带波动衰减误差=20p 101pαδ--=fs 缺省值为2HZ 【代码】[n,wn,bta,ftype]=kaiserord([0.3 0.45 0.65 0.8],[0 1 0],[0.01 0.1087 0.01]);%用kaiserord 函数估计出滤波器阶数n 和beta 参数h1=fir1(n,wn,ftype,kaiser(n+1,bta),'noscale'); [hh1,w1]=freqz(h1,1,256); figure(1) subplot(2,1,1)plot(w1/pi,20*log10(abs(hh1))) gridxlabel('归一化频率w');ylabel('幅度/db') subplot(2,1,2)plot(w1/pi,angle(hh1)) gridxlabel('归一化频率w');ylabel('相位/rad'); 【图形】00.10.20.30.40.50.60.70.80.91-100-5050归一化频率w幅度/d b0.10.20.30.40.50.60.70.80.91-4-2024归一化频率w相位/r a d用等波纹法设计：【解析】调用函数[n,fpts,mag,wt]=remezord(f ，a ，dev) f=[0.3 0.45 0.65 0.8] a=[0 1 0] dev=[0.01 0.1087 0.01]其含义同函数[n,wn,bta,ftype]=kaiserord （f ，a ，dev ，fs ）中的参数相同。

【代码】[n,fpts,mag,wt]=remezord([0.3 0.45 0.65 0.8],[0 1 0],[0.01 0.1087 0.01]);%用remezord 函数估算出remez 函数要用到的阶n 、归一化频带边缘矢量fpts 、频带内幅值响应矢量mag 及加权矢量w ，使remez 函数设计出的滤波器满足f 、a 及dev 指定的性能要求 h2=remez(n,fpts,mag,wt);%设计出等波纹滤波器 [hh2,w2]=freqz(h2,1,256); figure(2) subplot(2,1,1)plot(w2/pi,20*log10(abs(hh2))) gridxlabel('归一化频率w');ylabel('幅度/db') subplot(2,1,2)plot(w2/pi,angle(hh2)) gridxlabel('归一化频率w');ylabel('相位/rad'); 【图形】00.10.20.30.40.50.60.70.80.91-100-5050归一化频率w幅度/d b00.10.20.30.40.50.60.70.80.91-4-2024归一化频率w相位/r a d五、扩展练习例1:用凯塞窗设计一FIR低通滤波器，通带边界频率，阻带边界频率，阻带衰减不小于50dB。