当前位置：文档之家 › 第三章 统计描述

第三章 统计描述

  • 格式：ppt
  • 大小：1.47 MB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

第三章总体数量的统计描述

第三章总体数量的统计描述

• 第三章统计数 量的统计描述
• 第三章统计数 量的统计描述 Ex 根据表中各指标之间的关 系计算所缺数字。 系计算所缺数字。
工业总产值（万元） 工业总产值（万元） 计 划 完成计划% 实 际 完成计划 甲 乙 丙 合 计 680 600 2000 750 109．7 ．
2200
广东省民政职业技术学校欢迎您
广东省民政职业技术学校欢迎您
• 第三章统计数 量的统计描述
(二)按照总量指标反映的时间状况不同，分为时期总量 二 按照总量指标反映的时间状况不同 按照总量指标反映的时间状况不同， 指标与时点总量指标。 指标与时点总量指标。 时期总量指标是反映总体在某一段时期内发展变化 结果的总量指标。 结果的总量指标。 时点总量指标是反映总体在某一时刻上呈现、 时点总量指标是反映总体在某一时刻上呈现、存在 或达到的总数量指标。 或达到的总数量指标。 时期指标和时点指标的区别 时期总量指标在不同时间内的数值可以相加， 时期总量指标在不同时间内的数值可以相加，数值 的大小与时间长短有着直接的联系，它具有时间长度； 的大小与时间长短有着直接的联系，它具有时间长度； 相反，时点总量指标在不同时刻上的数值则不能相加， 相反，时点总量指标在不同时刻上的数值则不能相加， 数值的大小与时间长短没有着直接的联系， 数值的大小与时间长短没有着直接的联系，它不具有 时间长度。 时间长度。
广东省民政职业技术学校欢迎您
• 第三章统计数 量的统计描述
• • • •
统计原理习题集 P22 EX14 ——21 P24——26 EX1 ——28 P36——38 全部练习
广东省民政职业技术学校欢迎您
• 第三章统计数 量的统计描述
1、简单算术平均数
x=
2、加权算术平均数

Spss统计应用基础第三章N

Spss统计应用基础第三章N

3.10
标准化Z分数及其线性转换
• 3.10.1 统计学上的定义和计算公式 ，标准差 • Z分数的定义：从平均数为，
为 ，的总体中抽出一个变量值x,Z分 数表示的是此变量大于或小于平均数几 个标准差。 x • 计算公式： z


• T=10Z+50
• 3.10.2 SPSS中实现过程
3.8
峰度(Kurtosis)
3.8.1 统计学上的定义和计算公式 • 定义：描述某变量所有取值分布形态陡缓程度 的统计量。 • 峰度为0表示其数据分布与正态分布的陡缓程度相同； • 峰度大于0表示比正态分布高峰要更加陡峭，为尖峰。 • 峰度小于0表示比正态分布的高峰要平坦，为平顶峰。
1 n 4 4 Kurtosis ( xi x) / SD 3 n 1 i 1
3.3
众数(Mode)
3.3.1 统计学上的定义和计算公式 定义：众数是一组数据中，出现次数最多的那个 变量的值。 计算公式
⑴原始数据法
出现频数最多的那个数值就是众数。
例：7，4，7，2，6，7的众数是7。 ⑵频数分布表法 频数最多一组的组中值就是众数。当相邻的两个组频数 都是最多时，两组的分组点就是众数。
• 3.9.2 SPSS中实现过程
研究问题 某班41个学生身高分布，试求学生身高分布偏度。 实现步骤：
(1)单击Analyze菜单Descriptive Statistics中的 Frequencies命令 (2)将变量列表中的变量“身高”添加到Variable(s)框 中。 (3)单击下方的Statistics按钮，对话框中选统计的项目。 在Distribution框中选Skewness, 选好后单击 Continue,返回Friquencies对话框，单击OK，SPSS即 开始计算。

第三章描述性统计分析

第三章描述性统计分析

描述性统计分析指标

统计量可分为两类


一类表示数据的中心位置，例如均值、中位数、众 数等 一类表示数据的离散程度，例如方差、标准差、极 差等用来衡量个体偏离中心的程度。
描述单变量分布的三种方式

用数字呈现一个变量的分布 用表格呈现一个变量的分布 用图形呈现一个变量的分布
Frequencies

在交叉列联表中，除了频数外还引进了各种百分 比。例如表中第一行中的33.3％， 33.3％， 33.3 ％分别是高级工程师3人中各学历人数所占的比例 ，称为行百分比（Row percentage），一行的百 分比总和为100％；表中第一列的25.0％，25.0％ ，50.0％分别是本科学历4人中各职称人数所占的 比例，称为列百分比（Column percentage）， 一列的列百分比总和为100％，表中的6.3％，6.3 ％，12.5％等分别是总人数16人中各交叉组中人 数所占的百分比，称为总百分比（Total percentage），所有格子中的总百分比之和也为 100％。
例子

假设我们有以下的三组观测值：

观测A：11，12，13，16，16，17，18，21 观测B：14，15，15，15，16，16，16，17 观测C：11，11，11，12，19，20，20，20

这三组观测值的均值都是15.5，那么这三组数 据是否相似呢？
离散趋势
离散趋势的描述
本科 职称 高 级工 程师 Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total Count % within 职 称 % within 文 化 程 度 % of Total 1 33.3% 25.0% 6.3% 1 25.0% 25.0% 6.3% 2 33.3% 50.0% 12.5% 0 .0% .0% .0% 4 25.0% 100.0% 25.0%

统计学概论03

统计学概论03
n 1 n
式中G表示几何平均数, 表示各项标志值 表示各项标志值. 式中 表示几何平均数,xi表示各项标志值. 表示几何平均数
3-21
(2)加权几何平均数 )
加权几何平均数是各标志值fi次方的连乘积的 加权几何平均数是各标志值 次方的连乘积的 次方根,计算公式为: 次方根,计算公式为: G=
∑ fi
xik = ∑ ( xk ) k =n( xk ) k ∑
i =1 i =1 n n
k xk = ∑ xi / n i =1
n
1/ k
称为k阶幂平均数, 取不同的整数值时, 称为 阶幂平均数,当k 取不同的整数值时, 阶幂平均数 幂平均数就给出不同的数值平均数计算公式. 幂平均数就给出不同的数值平均数计算公式.
∑ x k1 n
∑ x k2 ≤ n
1 k
1 k2
因为算术平均数,几何平均数,调和平均数都是幂 因为算术平均数,几何平均数, 平均数的k阶数由 递减为0又减为 的特例, 阶数由1递减为 又减为-1的特例 平均数的 阶数由 递减为 又减为 的特例,三者之 间的一般数量关系为: 间的一般数量关系为:调和平均数小于几何平均数 小于算术平均数;当各变量相等时, 小于算术平均数;当各变量相等时,调和平均数等 于几何平均数等于算术平均数. 于几何平均数等于算术平均数.
m1 + m2 + + mn = H= m1 m2 mn + ++ x1 x2 xn
∑m
i =1 n
n
i
mi ∑x i =1 i
在权数选择合适时, 在权数选择合适时,加权调和平均数实际上 是加权算术平均数的变形: 是加权算术平均数的变形:
∑m

第三章 离散趋势的统计描述

第三章 离散趋势的统计描述

方差的计算公式为：

2
xi N
xi x n 1
2
式（3-4）
S
2
2
式（3-4）
标准差：
由于每一离均差经过平方，使原来 观察值的度量单位也都变为平方单 位，为了还原成为原来的度量单位， 所以又将方差开平方，这就是标准 差（standard deviation）。
试估计该地正常女子血清甘油三脂在1.10 mmol/L以 下者占正常女子血清甘油三脂总人数的百分比。 将X=1.10代入标准正态变量变换公式，得：
1.10 1.14 u 0.14 0.29
计算正态曲线下面积实例
查附表1，在表的左侧找到－0.1，在 表的上方找到0.04，，两者的相交处为 0.4443=44.43%。 即该地正常女子血清甘油三脂在 1.10mmol/L以下者，估计占总人数的 44.43%。 例2见P22。
实例图示
1.8 1.5 1.2 0.9 0.6 0.3 0.0 0 0.5 1 X 1.5 2
44.43％
概率密度函数与累积分布函数
f(X) F(X)
1 0.8 0.6 0.4 0.2 0 -4 -3 -2 -1 0
X
1
2
3
4
三、 正态分布的应用
• • • • • 一种最常见、最重要的连续分布 很多正常人的生理、生化指标的理论分布 数理统计中发展得最为完善的一种分布 很多统计推断都是在正态分布条件下进行 很多非正态分布的资料，当观察例数足够 多时，可以用正态分布作为它的极限分布 • 有时，也将非正态分布资料转化为正态分 布来处理
一、医学参考值范围的概念
• 又称参考值范围(reference range)， 是指正常人的各种生理、生化数据、 组织或排泄物中各种成分含量的测 定值的波动范围。 • 常用95％的参考值范围

数据分布特征的统计描述

数据分布特征的统计描述

x xx1x2...xn
n
n
均值，即算术平均数
x 标志值或变量值
见49页例题
20
2、加权法：分组且各组标志值出现的次数 （权数 f ）不相等时，公式：
x xfx1f1x2f2...xnfn
f
f1f2...fn
x 为标志值，又称变量值； f 为各组标志值出现的次数
返回本节首页
21
某厂工人生产情况
第三章 数据分布特征的统计描述
除了统计图和统计表之外，还可以用少量 的特征值（代表值）对数据分布的数量规 律进行精确、简洁的描述。
1
离中趋势：即反映各数据远离中心值的程度 因为即使现象的集中趋势相同，其离中趋势 也可能不同。
离中趋势 (分散程度)
两个不同的曲线表示两个不同的总体，它们的 集中趋势相同但离中趋势不同。
“150个企业的平均计划完成百分数” 就是“150个企 业总的计划完成百分数”。
企业总计划完成百分数 = 总实际数 / 总计划数
计划完成 百分数％ 105~110 110~120 120~130
合计
企业 数n 30 70 50 150
计划产值 f
5700 20500 22500 48700
x
xf
％ 实际值
m 1m x
46
举例:
某蔬菜单价早中晚分别为0.5、0.4、 0.25（元/斤） （1）早中晚各买1元，求平均价格 （2）早中晚各买1斤，求平均价格 （3）早中晚各买2元、3元、4元，求平均价格 （4）早中晚各买2斤、3斤、4斤，求平均价格
47
（1）问：用调和平均。先求早、中、晚购买的斤 数。早 1/0.5=2(斤) 、中 1/0.4=2.5(斤)、晚 1/0.25=4(斤)

第三章 分类变量的统计描述 第一节 常用相对数

第三章 分类变量的统计描述 第一节 常用相对数
第三章 分类变量的统计描述 第一节 常用相对数
相对数：率、构成比、相对比等指标。
一、构成比=（某一组成部分的观察单位数/
同一事物各组成部分观察单位总数）*100% 1）各部分构成比之和为100% 2）某一部分所占的比重增大，其他部分的比 重会相应减少。 二、率=（发生某现象的观察单位个数/可能 发生某现象的观察单位总数）*100%
三、比
1.两个有关联指标之比。 2.用于性质不同的两个有联系指标之比。
第二节 应用相对数时的注意事项
1.构成比与率，是意义不同的两个指标。
2.样本含量太小时，不宜计算相对数 3.对各组观察例数不等的几个率，不能直接
相加求其总率。 4.在比较相对数时应注意资料的可比性。
（三）应用标准化法的注意事项 1.标准化职能解决不同人群内部构成不同对其总率 有影响的情况。 2.标准化后的标化率，已经不再反映当时当地的实 际水平，只表示相互比较的几组资料间的相对水平。 3.由于选择的共同标准不同，计算出来的标准化率 会有所不同，但相对水平不变。 4.各年龄组率间若出现明显交叉，宜比较年龄组死 亡率，而不用标准化法。

第四节 动态数列及其分析指标
一、绝对增长量
1.累积增长量 2.逐年增长量 二、发展速度 1.定基发展速度可以反映事物在一定时期的
发展速度。 2.环比发展速度
三、增长速度
增长速度=发展速度-1 四、平均发展速度和平均增长速度。 平均增长速度=平均发展速度-1
第三节 标准化法
除人口构成
不同对人群总率的影响，使算的标准化率具 有可比性。 （一）直接法计算标化率需2个条件 1.资料条件 2.选择标准
（二）直接法标化率的计算

统计学(第3章)

统计学(第3章)
第三章 统计数据的整理 6
4、定比尺度（比率尺度 ratio scale）
是对事物之间比值的一种测度，可用
于参数与非参数统计推断。 特征：

除区分事物的类别、进行排序、比较大 小，而且还可以进行加减乘除运算。 具有绝对零点，即“0”表示“没有” 或“不存在”。 所有统计量都可以对其进行分析。与定 距尺度的唯一区别是有绝对固定的零点。
第三章 统计数据的整理 10
3、观察数据和实验数据


观察数据：通过调查或观测而得 到的数据。 实验数据：通过控制实验对象而 收集的数据。
第三章 统计数据的整理
11
4、直接数据和间接数据
直接数据：即原始数据。
间接数据：已加工整理过的数据。
第三章 统计数据的整理
12
第二节 统计整理的含义和步骤



当异距分组时，各组的次数还受 到组距不同的影响。为消除异距 分组的这种影响，须计算频率密 度（或次数密度），计算公式： 频数密度 = 频数/组距 频率密度 = 频率/组距
第三章 统计数据的整理
36
二、分布数列的编制
将原始资料按其数值大小重新排列 2. 确定全距 3. 确定组距和组数 4. 确定组限 5. 编制变量数列 示例3-5
第三章 统计数据的整理
某地人口
21
（三）按分组标志的不同性质分
品质分组（属性分组）：是将总体按
品质（或属性）标志进行分组。如企 业按经济成份、企业规模，职工按性 别、文化程度分组等。 数量分组（变量分组）：是将总体按 数量标志进行分组，如企业按职工人 数、劳动生产率分组，职工按工龄、 工资分组等。
第三章 统计数据的整理 31
4、开口组的组距与组中值

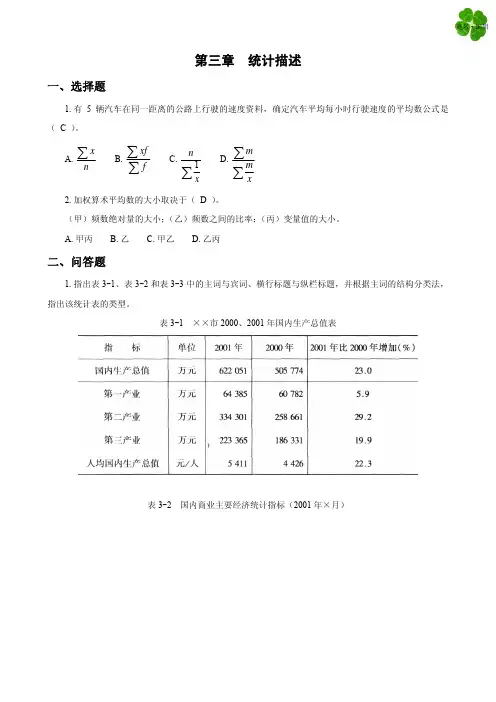
统计描述课后习题解答

统计描述课后习题解答

第三章 统计描述一、选择题1.有5辆汽车在同一距离的公路上行驶的速度资料，确定汽车平均每小时行驶速度的平均数公式是（ C ）。

A.xn∑B.xff∑∑C.1nx∑D.mmx∑∑2.加权算术平均数的大小取决于（ D ）。

（甲）频数绝对量的大小；（乙）频数之间的比率；（丙）变量值的大小。

A.甲丙B.乙C.甲乙D.乙丙二、问答题1.指出表3-1、表3-2和表3-3中的主词与宾词、横行标题与纵栏标题，并根据主词的结构分类法，指出该统计表的类型。

表3-1 ××市2000、2001年国内生产总值表表3-2 国内商业主要经济统计指标（2001年×月）表3-3 ××市饮食业机构、人员基本情况（2001年）答：表3-1为主词简单分组表。

表3-2为主词复合分组表。

表3-3为主词复合分组表，一部分主词（市、县、县以下）放置在宾词的位置。

2.在教材第三章的例3-6中，按调和平均法和按算术平均法计算的结果一致，根据幂平均数是参数k 的单调不减函数的性质，算术平均数≥调和平均数，这两者是否存在矛盾?答：不存在矛盾，因为上面所说的算术平均数≥调和平均数的前提条件是每个变量的权数是相等的，而例3-6中各变量的权数不相等。

所以两者也就不存在矛盾。

三、计算题1.抽样调查某省50户城镇居民平均每人全年可支配收入资料如表3-4所示。

表3-4 居民年人均可支配收入单位：百元要求：（1）试根据上述资料编制次（频）数分布数列；（2）编制向上和向下累计频数、频率数列；（3）根据所编制的次数分布数列绘制直方图、折线图与曲线图，并说明其属于何种分布类型；（4）根据所编制的向上（向下）累计频数（频率）数列绘制累计曲线图；（5）根据频数分布曲线图说明居民年人均可支配收入的分布类型。

解：（1）表3-5（2）表3-6表3-7（3）可以使用Excel的数据分析工具中的“直方图”工具生成如第（1）题所示的次数分布数列以及相应的直方图和折线图等。

第三章 描述性统计量

第三章 描述性统计量
2020/6/24
第一节 刻画数据集中程度的特征量
▪ 依据各种统计指标的具体代表意义和计算方 式的不同，可以将其归纳为数值平均数和位 置平均数两大类。
▪ 数值平均数就是对所有各项数据计算的平均 数。因此它能够概括反映所有各项数据的平 均水平。
▪ 常用的数值平均数有算术平均数、调和平均 数和几何平均数。
2020/6/24
第一节 刻画数据集中程度的特征量
▪ 位置平均数是根据数据集中处于特殊位置的 个别单位或部分单位的数据来确定的代表值， 因此数据集中某些数据的变动，不一定会影 响到位置平均数的水平，尽管如此，位置平 均数对于整个数据集仍具有非常直观的代表 性。
▪ 常用的位置平均数有众数、中位数和其他分 位数等。
2020/6/24
第一节 刻画数据集中程度的特征量
▪ 一、算术平均数（均值）、中位数和众数 ▪ （一）算术平均数（均值）（Mean)(Average)
在刻画数据的“平均”特性的特征值中，最普遍最 常用的是算术平均数，在统计上称为均值。 均值的计算：
2020/6/24
x
1 n
xi
fi
第一节 刻画数据集中程度的特征量
2020/6/24
第一节 刻画数据集中程度的特征量
▪ 例16（P21）关于工人月薪的调查见下表
2020/6/24
每月收入 ≤400
（400，500】 （500，600 】 （600，700 】
﹥700 合计
分类平均 280 460 550 670 850
工人数 10 28 42 50 20 150
位数的近似值。 计算公式为： m = I +i(n/2-F)/f （下限公式） 其中： I表示中位数所在区间的下限值

3.计量资料统计(1)描述

3.计量资料统计(1)描述
2、确定组段数（即组数）、组距： 频数表一般设 8 ~ 15个组段。 组距(class interval) = R / 组段数。往往取近似值。
3、确定组段，列表划记： 每个组段的起点称下限，终点称上限。 第一组段要包括最小值，最后一个组段要包括最大值。 各组段从本组段的“下限”开始，不包括本组段的
“上限”，最末一组段应同时写出其上下限。
计算方法：
l 直接法：当观察单位的个数不多时可直接计算。公式 为：
x x1 x2 xn
X
n
n
l 加权法：当资料中相同观察值的个数较多时，可将相
同观察值的个数，即频数f，乘以该观察值X，以代替相同
观察值逐个相加。
x f1 x1 f 2 x2 f m xm f
f1 f2 fm
第三章 数值变量资料的 统计描述
第一节 数值变量资料的频数表
频数就是观察值的个数。频数分布 就是观察值在其取值范围内分布的情况。 要了解数值变量资料的分布规律，当观 察单位较多时，可编制频数分布表(简称 频数表)和绘制直方图。
一、频数表（equency table）的编制
1、找出观察值中的最大值(Max)、最小值(Min)和极差(R) R=Max—Min
10
125
1250
126~
4
127
508
128~
3
129
397
130~
2
131
262
132~134
1
133
133
合计
110
13194
二、几何均数（geometric mean）
记作G。 该指标适用于： ①变量值呈等比级数关系的资料，如 血清抗体滴度的资料； ②对数正态分布的资料，即某些偏态 分布的资料，当将变量值取对数后又呈现 正态分布的资料。

第三章统计数据分布特征的描述

第三章统计数据分布特征的描述

第三章统计数据分布特征的描述统计数据分布特征的描述是统计学中非常重要的一个概念，它用于对数据进行系统化的描述和分析。

统计数据分布特征的描述包括位置参数、散布参数和形状参数。

位置参数描述了数据集中心位置的特征。

最常用的位置参数是均值和中位数。

均值是指所有数据值的总和除以数据个数，它能够反映数据集的平均水平。

中位数是将数据值按大小排序后的中间值，它能够反映数据集的中心位置。

均值对异常值比较敏感，中位数能够较好地排除异常值的干扰。

散布参数描述了数据集的离散程度。

最常用的散布参数是方差和标准差。

方差是指每个数据值与均值之差的平方和的平均值，它能够反映数据集的离散程度。

标准差是方差的平方根，它与数据的单位相一致，常用于衡量数据的波动性。

方差和标准差越大，表示数据的离散程度越大。

形状参数描述了数据集的分布形状。

常用的形状参数包括偏度和峰度。

偏度是指数据分布的不对称程度，大于0表示右偏，小于0表示左偏，等于0表示对称。

偏度能够反映数据集的分布形态。

峰度是指数据分布的尖锐程度，大于0表示尖锐，小于0表示平坦，等于0表示与正态分布相似。

峰度能够反映数据集的尖峰或扁平程度。

除了这些常见的参数之外，还有其他一些描述统计数据分布特征的方法，如四分位数和箱线图。

四分位数是将数据分为四等分的值，它包括上四分位数、下四分位数和中位数。

上四分位数是四分之三分位数，下四分位数是四分之一分位数。

箱线图是以箱子和线段的形式展示数据分布特征，箱子的上边界和下边界分别代表上四分位数和下四分位数，箱子的中线代表中位数，箱子的长度代表数据的离散程度。

统计数据分布特征的描述对于研究数据的特征、提取有效信息以及进行统计推断都非常重要。

了解数据的位置、散布和形状特征能够帮助研究者更好地理解数据集的性质和规律。

在实际应用中，统计数据分布特征的描述还可以帮助决策者进行决策，例如对于质量控制的判断和产品的质量评估等。

综上所述，统计数据分布特征的描述是对数据集进行系统化描述和分析的重要工具。

体育统计方法与实例第三章 统计描述

体育统计方法与实例第三章 统计描述

第一节 描述统计
一、集中量数指标包括： 1 算术平均数（Average） 2 中位数（Median） 3 众数（Mode） 4 百分位数（Percentile）
一、集中量数指标
1. 算术平均数（Average）
（1）定义：所有同质数据的总和除以数据的个数所得的商， 即为该组数据的算术平均数，简称平均数、均数或均值。 就是说，如果有一组数据 xi (I=1,2,3…n),把
四分差（四分位差）是一组数据中第三四分位数与 第一四分位数之差的一半。记
为Q
计算公式为：
Q Q3 Q1 2
(3-1-7)
四分差的意义是除去两端各四分之一的部分，用剩余 中间的一半来测定四分之一的距离大小。它去掉了极端数 据，不受极端值的影响，在反映数据的离散程度方面较之 极差略准确一些。它适用于定量数据。
在表3-1-3中，频数最多的是第5组，频数为25，该组的 组中值为（330+346）/2=338，故本组数据的众数为338. 注意：中位数、众数受极端数据（数值非常大或非常小）的 影响较小。
算术平均数、中位数、众数间的关系:
当频数分布呈完全对称分布时，算术平均数、中位数、 众数三者相同，如图3-1-1所示。
图3-1-1 对称分布
当频数分布呈正偏态时，算术平均数大于中位数、
众数小于中位数，如图3-1-2所示。
图3-1-2 正偏态分布
当频数分布呈负偏态时，算术平均数小于中位数、 众数大于中位数，如图3-1-3所示。
图3-1-3 负偏态分布
平均数、中位数和众数都是描述数据集中趋 势的统计量，它们分别适用于不同分布的数据资 料。平均数适用于无异常值的正态或近似正态分 布的数据资料；中位数适用于存在异常值且严重 偏态的数据资料；众数适用于分布不匀，而个别 数据重复次数较多的数据资料。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平均计划完成程度
xf 95 % 100 105 % 800 115 % 100 1050 105 % 100 800 100 1000 f
1-6
（二）算术平均数的数学性质

1.各单位标志值与算术平均数的离差之和等于0。
(x x) x x nx nx 0 ( x x ) f xf x f x f x f 0
或
4.变量线性变换的平均数等于变量平均数的线性变换。
若 y a bx ，则 y a b x
例如： a 2， b 1，即 y 2 x
当变量 x 取不同变量值时，
x1 2 y 1 2 2 4 x2 4 y2 2 4 6
y 46 5 2
1300 3500 3600 8400
播 种 面 积 （ 亩 ）m
x
500 700 800
—
2600 5000 4500 12100
平均亩产
（三）在运用加权调和平均数时，各组权数相等，就可以采用简单调和平均数。
m 当 m 1 m 2 m n时， H nm n m x m 1 1 x x
95 105 11 5
—
企业数
实际销售额 （万元）
5 8 2 15
95 840 11 5 1050
计划完成程度
实际完成数 计划任务数
销售计划完 成程度（%） 90— 100 1 0 0 — 11 0 11 0 — 1 2 0 合计
组中值（%）
x
95 105 11 5
—
企业数
实际销售额
计划销售额 （万元）
权数
加权
日产量（件） 工人数

xi f i fi
fi
i 1
xf f
x
20 21 22 23 24 25 合计
f
10 20 30 60 50 30 2 00
xf
2 00 4 20 6 60 1 380 1 200 7 50 4 610
xf x 4610 23 . 05 ( 件 ) 200 f
总合格率 90 % 80 % 70 % 50 . 4 %
（二）应用：在某些情况下，若 总体总量是由标志值相乘得出， 这时平均数就应该用几何平均数 的方式来计算。
与算术平均数不同
平均工资 工资总额 工人数
这样平均合格率为
平均合格率
n
x 3 90 % 80 % 70 %

当各组的权数相同时。 当分布数列完全对称时。
x
1
1
2
2
n
n
f


nA
n
(4)加权算术平均数的频率公式。
x x1 f 1 x 2 f 2 x n f n f f f f x1 1 x 2 2 x n n x f f f f f 1-5
3.正确选择权数——当从相对数或平均数求平均数时
例：某管理局所属15个企业销售计划完成情况资料如下表：

选择权数的准则：最终的平 均指标的涵义要符合原来相 对指标(平均指标)本身的涵义
计划完成程度 实际完成数 计划任务数
组中值（%） 企业数
销售计划完 成程度（%） 90— 100 1 0 0 — 11 0 11 0 — 1 2 0 合计
平均日产量
m 4610 H 23 . 05 ( 件 ) m 200 x
1-10
2.从相对数或平均数求平均数时 例：某管理局所属15个企业销售计划完成情况资料如下表：
销售计划完 成程度（%） 90— 100 1 0 0 — 11 0 11 0 — 1 2 0 合计 组中值（%）
x
数值平均数：算术平均数，调和平均数，几何平均数。 位置平均数：中位数，众数。
1-2
Байду номын сангаас
(三)两种平均数


二、算术平均数
算术平均数 总体标志总量 总体单位总量
钢产量 全国总人口数
强度相对指标：
人均钢产量
算术平均数： 全国钢铁工人平均钢产

量
钢产量 全国钢铁工人数
（一）算术平均数的计算 1.简单算术平均数：未分组的资料。
x x x x
x1
x
x x x x
证明：设
xn
2.各单位标志值与算术平均数的离差平方和为最小。
设 x 0 为任意值，
2 2 ( x x ) ( x x0 ) 2 2 ( x x ) f ( x x0 ) f
x 0 x C ,即 x 0 x C
1-12
例：已知某地区甲、乙、丙三个乡粮食平均亩产和粮食总产量 如表，求全区平均亩产。
乡名 甲 乙 丙 合计
乡名 甲 乙 丙 合计
平均亩产（公斤） 粮食总产量（吨）
500 700 800
—
平 均 亩 产 （ 公 斤 ）x
1300 3500 3600 8400
平均亩产
粮食总产量 播种面积
m 粮食总产量（吨）
1-7
3.若对每一个标志值加、减、乘、除一个常数A，则平均数也加、 减、乘、除这个常数A。
( x A ) x nA x A n n Ax A x A x n n

或
( x A ) f xf Af x A f f Axf A xf A x f f
p 1 p 0 p 0 r p 0 (1 r )
p 2 p 1 p 1 r p 1 (1 r ) p 0 (1 r )(1 r ) p 0 (1 r ) 2

p2 p0 p0 2r

p n p 0 p 0 nr

p n p 0 (1 r ) n
m 8400000 m 12100 x
694 . 2 (公斤 )
1-13
四、几何平均数

（一）公式 1.简单几何平均数：
G n x1 x 2 x n n x
2.加权几何平均数
G
f
x 1x
1
f
f 2
2
x
f n
n

f
x
f
例：1.某产品经过三个流水连续 作业的车间加工生产而成，本月 第一车间的产品合格率为90%， 第二车间的产品合格率为80%， 第三车间的产品合格率为70%。 则全厂的总合格率为
第三章 统计描述
第一节 分布的集中趋势 第二节 分布的离散趋势 第三节 分布的偏度与峰度


1-1
第一节 分布的集中趋势

一、统计平均指标概述

（一）定义：是同类社会经济现象在一定时间、地点条件下 所达到的一般水平，是度量分布集中趋势或中心位置的指标。

（二）作用：

1.反映总体各单位变量分布的集中趋势和一般水平。 2.比较同类现象在不同单位的发展水平。 3.比较同类现象在不同时期的发展变化趋势或规律。 4.分析现象之间的依存关系。
m
200 420 660 1380 1200 750 4610
m x
10 20 30 60 50 30 200
3.加权调和平均数
m H 1 1m m x x m
f xf
（二）调和平均数的应用场合 1.作为算术平均数的变形使用。权数 m为各组的标志总量。即 m xf
m xf xf H m f x xf x
2 2 .5 4 .5
1-9
三、调和平均数（H）
（一）调和平均数的公式 1.调和平均数：又称倒数平均数，是标志值倒数的算术平均数的 倒数。 例：某工厂工人日产零件数资料： 2.简单调和平均数
n H 1 1 1 x x n
日产量（件） 零件数 工人数
x
20 21 22 23 24 25 合计
2 2
2 ( x x 0 ) x ( x C ) ( x x ) C
( x x ) 2 2 C ( x x ) nC ( x x ) 2 nC
nC
2
2
2
0
( x x 0 ) 2 ( x x ) 2 ,即 ( x x ) 2 为最小。
x1 x 2 x n n

3
50 . 4 % 79 . 58 %
1-14
平均产量
总产量 工人数

x1 x 2 x n n
例2：以复利计算利息。
假设 p 0 为本金，

r 为利率，
p n 为 n 年后的本利和。
若以单利计算：
p1 p 0 p 0 r
若以复利计算：
1-4
（2）组距式加权算术平均数
例：某年我国80个产棉大县的 分配数列如表。

按产棉量分 组（百吨） 1 00 以 下 1 00 ～ 20 0 2 00 ～ 30 0 3 00 ～ 40 0 4 00 以 上 合计
县数
组中值
f
x
50 15 0 25 0 35 0 45 0
—
xf
以组中值作为各组的代表值， 假定各组标志值在组内分布 是均匀的。
x 4610 23 . 05 ( 件 ) 200
日产量（件） 工人数

x
20 21 22 23 24 25 合计
f
10 20 30 60 50 30 2 00