坡度坡向的提取算法

实验五DEM坡面地形因子提取实验目的：通过数字高程模型（DEM）数据提取坡度和坡向地形因子，以分析地形特征对水文过程和土地利用分布的影响。

实验步骤：1.数据准备a) 获取高分辨率的地形DEM数据，可以选择使用Lidar数据或者采用其他方式获取DEM数据。

b)进行数据预处理，包拟合DEM数据，去除噪声和突出值等。

2.坡度计算a)在DEM上采样，计算每个像元上的坡度。

b)坡度计算可以通过以下公式进行计算：Slope(i,j) = arctan(sqrt((dz/dx)^2 + (dz/dy)^2))其中，Slope(i,j)代表坡度， dz/dx代表DEM在x方向的梯度，dz/dy代表DEM在y方向的梯度。

3.坡向计算a)在DEM上采样，计算每个像元上的坡向。

b)坡向计算可以通过以下公式进行计算：Aspect(i,j) = arctan(dz/dx / dz/dy)其中，Aspect(i,j)代表坡向， dz/dx代表DEM在x方向的梯度，dz/dy代表DEM在y方向的梯度。

4.地形指数计算a)根据坡度和坡向的计算结果，可以进一步计算其他地形指数，例如地形湿度、地形开阔度等。

b)地形湿度可以通过计算每个像元周围的流通路径长度来估算。

c)地形开阔度可以通过计算每个像元周围的可见面积来估算。

5.结果分析a)可视化坡度和坡向地形因子，以了解地形特征。

b)利用地形指数，可以分析地形特征对水文过程和土地利用分布的影响。

实验结果分析：通过提取DEM的坡度和坡向地形因子，可以分析出地形特征，进而对水文过程和土地利用分布进行预测和分析。

例如，通过分析坡度可以了解一个地区的地势起伏程度，从而对洪水灾害的发生概率进行预测。

通过分析坡向可以了解水流在地表的流向，从而对土壤侵蚀和水资源分布进行预测。

此外，通过计算其他地形指数，还可以分析地形湿度和地形开阔度对生态环境的影响，为环境管理和规划提供数据支持。

总结：本实验通过DEM数据的处理和分析，提取了坡度和坡向地形因子，并通过计算其他地形指数，以分析地形特征对水文过程和土地利用分布的影响。

dem坡度坡向计算
坡度是地面特定区域高度变化比率的量度,坡向是斜坡方向的量度.坡向定义为坡面法线在水平面上的投影的方向。

当基于DEM计算坡向时,通常定义坡向为:过格网单元所拟合的曲面片上某点的切平面的法线的正方向在平面上的投影与正北方的夹角,即法方向水平投影向量的方位角,由数学分析知,设曲面z=f<x,y style="margin: 0px; padding: 0px;">在点〔x0,y0,z0〕的切平面方程为:z=Ax+By+C=fx<x0,y0 style="margin: 0px; padding:
0px;">x+fy<x0,y0 style="margin: 0px; padding: 0px;">y+C,在该点的坡向为:β=arctan,但根据此式计算的β在〔-π/2,π/2〕中取值,而坡向应在〔0,2π〕中取值。

坡度计算公式是什么该如何计算
坡度是地表单元陡缓的程度，那么坡度的计算公式是怎样的呢?下面是由编辑为大家整理的“坡度计算公式是什么该如何计算”，仅供参考，欢迎大家阅读本文。

坡度计算公式是什么
i=h/lx100%。

公式描述：公式中h为高度差，l为水平距离，i为坡度。

表示坡度最为常用的方法，即两点的高程差与其水平距离的百分比，其计算公式如下：坡度=(高程差/水平距离)x100%。

坡度1%是指路程每100米,垂直方向上升(下降)1米。

坡度是哪两边的比
坡度是对面和邻边的比，通常把坡面的垂直高度h和水平宽度l的比叫做坡度，即tan a值 (a为斜坡与水平面夹角)
坡度系数：即用百分数来表示坡面与水平投影面的比值
坡度系数=1/tan a×100%(a为斜坡与水平面夹角)
拓展阅读：坡度比1:1.5是什么意思?
坡度比1：1.5的意思是：坡的高度与坡的宽度之比值为1比1.5，即2/3。

也就是斜坡的坡角的正切值是2/3。

如果边坡高度是1米的话，那么边坡宽度就是1.5米，它们的比值是1：1.5。

坡度比也叫坡比，是坡面垂直高度和水平宽度的比，通常取边坡高度为1，用1：m来表示;也可用边坡角(边坡与水平面的倾角)表示。

常把坡面的垂直高度h和水平宽度l的比叫做坡度，即tan∠a值(正切，∠a为斜坡与水平面夹角)，即“爬升高度除以在水平面上的移动距离”。

面向林业小班的坡度、坡向及坡位提取算法研究在林业管理中，对坡度、坡向及坡位的准确提取对于评估森林资源、规划林业活动以及研究地形对林木生长的影响具有重要意义。

本文将探讨面向林业小班的坡度、坡向及坡位提取算法的研究。

一、引言随着地理信息系统（GIS）技术的不断发展，地形分析在林业管理中的应用越来越广泛。

坡度、坡向及坡位作为重要的地形因子，对于林业资源的合理利用和科学管理具有指导意义。

为此，研究高效的提取算法对于提高林业地形分析的精度和效率至关重要。

二、坡度提取算法1.数字高程模型（DEM）是进行坡度提取的基础数据，常用的坡度提取算法有以下几种：（1）最陡下降法：计算每个栅格单元的最陡下降方向，进而得到坡度。

（2）二阶导数法：通过对DEM进行二阶导数运算，得到坡度。

（3）三阶不带权最小二乘法：对DEM进行三阶不带权最小二乘法运算，获取坡度。

2.针对林业小班的特点，可选用适合的坡度提取算法，如三阶不带权最小二乘法，以提高提取精度。

三、坡向提取算法1.常用的坡向提取算法有：（1）梯度方向法：通过计算DEM的梯度方向，得到坡向。

（2）最大坡降法：寻找每个栅格单元的最大坡降方向，作为坡向。

（3）加权坡向法：考虑相邻栅格的坡向信息，对当前栅格的坡向进行加权计算。

2.针对林业小班的实际需求，可以选用梯度方向法或加权坡向法进行坡向提取。

四、坡位提取算法1.坡位提取主要依据地形位置指数（TPI），计算方法如下：TPI = (DEM - 平均高程) / 标准差2.基于TPI，可以将地形分为以下几类：（1）山顶：TPI > 0 且为局部最大值。

（2）山脊：TPI > 0 且在山顶两侧。

（3）山谷：TPI < 0 且为局部最小值。

（4）山脚：TPI < 0 且在山谷两侧。

3.针对林业小班的特点，可以结合TPI和地形类别进行坡位提取。

五、结论本文针对林业小班的坡度、坡向及坡位提取算法进行了研究，探讨了不同算法的适用性。

地形测绘技术中的地貌特征提取与分析方法引言地形测绘技术是通过测量和分析地球表面的形状和特征来获取地形信息的一项重要技术。

在地理信息系统、城市规划、环境保护等领域中，地形测绘技术的应用越来越广泛。

地貌特征的提取和分析是地形测绘中的关键步骤，通过这些方法，我们可以对地球表面的地貌特征进行深入研究并获取有价值的信息。

一、数字高程模型数字高程模型（Digital Elevation Model，简称DEM）是地形测绘中常用的一种数据模型，它以矩阵形式表示地球表面的高程信息。

DEM可以通过多种方式获取，包括航空摄影测量、遥感影像解译、全球定位系统等。

在DEM中，每个格点都包含一个高程数值，通过对这些数据进行分析，可以提取地貌特征。

二、坡度和坡向分析坡度和坡向分析是地貌特征提取的常用方法，通过计算DEM中每个格点的坡度和坡向数值，可以揭示地表的起伏变化。

坡度指的是地面上某一点的斜率大小，通常以百分比或角度表示；坡向指的是地表某一点的指向，一般以方位角表示。

通过坡度和坡向的分析，我们可以获得地球表面的地势特征，比如山脉和河流的走向等。

三、山体阴影分析山体阴影分析是一种基于光照模型的地貌特征提取方法。

通过模拟太阳光照射地球表面，可以生成山体的阴影图像。

在阴影图像中，暗区代表山体的凹陷部分，亮区代表山体的凸起部分。

通过对山体阴影图像的分析，我们可以获得地貌特征中的山谷、山脊等信息。

四、地貌湿度指数地貌湿度指数是一种基于遥感数据的地貌特征提取方法。

通过分析植被覆盖的水汽蒸发和土壤含水量等因素，可以计算出不同地区的地貌湿度指数。

地貌湿度指数可以反映地表的湿润程度，对于研究地表的水域分布、植被类型等有重要意义。

通过地貌湿度指数的分析，可以了解地球表面的水文特征。

五、地貌类型分类地貌类型分类是一种将地球表面的地貌特征划分为不同类别的方法。

通过对DEM数据进行分类和聚类分析，可以将地表划分为山地、平原、台地等不同的地貌类型。

坡度计算方法坡度是指地面或道路的倾斜程度，通常用百分比或角度来表示。

在工程设计、建筑施工、道路规划等领域，坡度计算是非常重要的。

正确的坡度计算可以保证工程的稳定性和安全性。

本文将介绍坡度计算的方法，希望能对大家有所帮助。

首先，我们来介绍坡度计算的基本公式。

坡度通常用百分比来表示，计算公式为：坡度百分比 = (垂直高度 / 水平距离) × 100%。

其中，垂直高度是指起点和终点之间的高差，水平距离是指起点和终点之间的水平距离。

通过这个公式，我们可以快速计算出坡度的百分比。

除了百分比表示法，坡度也可以用角度来表示。

计算公式为：坡度角度 = arctan(垂直高度 / 水平距离)。

其中，arctan是反正切函数。

通过这个公式，我们可以将坡度转换为角度表示，更直观地理解坡度的大小。

在实际工程中，我们可能会遇到复杂的地形和道路情况，需要计算不同部分的坡度。

这时，我们可以采用分段计算的方法。

将整个坡度分成若干小段，分别计算每段的坡度，然后将它们相加得到整体坡度。

这样可以更精确地掌握地形的变化情况。

此外，对于某些特殊情况，比如曲线道路或不规则地形，我们可能需要采用更复杂的方法来计算坡度。

这时，我们可以借助专业的测量仪器，比如全站仪或水准仪，来进行精确测量和计算。

这些仪器可以帮助我们获取更准确的数据，保证工程的质量和安全。

总之，坡度计算是工程设计和施工中不可或缺的一部分。

通过本文介绍的方法，我们可以快速、准确地计算坡度，保证工程的稳定性和安全性。

希望大家能够在实际工作中灵活运用这些方法，做出更优秀的工程成果。

坡位的提取方法一、引言坡位是地形和地貌的重要特征之一，对于地理环境的分析和研究具有重要意义。

在地形数据处理中，提取坡位是一个常见的任务。

本文将介绍几种常用的坡位提取方法，并对其原理和适用范围进行分析。

二、高程差法高程差法是一种简单直接的坡位提取方法。

它基于地形起伏的高程差，通过计算两点之间的高程差来确定坡位。

具体步骤如下：1. 选择两个相邻点A和B，计算它们之间的高程差，即ΔH = HB - HA。

2. 根据地理坐标系，计算两点之间的水平距离d。

3. 计算坡度tanα = ΔH / d。

4. 根据坡度划分坡位等级。

高程差法的优点是简单易行，适用于小范围地形的坡位提取。

然而，它忽略了地形曲率和地形变化的复杂性，对于大范围地形的坡位提取效果较差。

三、倾斜度法倾斜度法是一种基于地形曲率的坡位提取方法。

它通过计算地形的倾斜度来确定坡位。

具体步骤如下：1. 在地形数据上选择一个点P，计算该点的倾斜度。

2. 倾斜度的计算可以使用数值方法或近似计算方法。

数值方法通过计算地形数据的导数来确定倾斜度，而近似计算方法则通过邻域点的高程差来估计倾斜度。

3. 根据倾斜度划分坡位等级。

倾斜度法考虑了地形曲率的影响，适用于复杂地形的坡位提取。

然而，倾斜度法对地形数据的分辨率和精度要求较高，且计算复杂度较大。

四、流向法流向法是一种基于水流流向的坡位提取方法。

它通过模拟水流的流向来确定坡位。

具体步骤如下：1. 在地形数据上选择一个点P，确定该点的流向。

2. 流向的确定可以使用流向算法，如D8算法或D∞算法。

这些算法基于地形数据的梯度和方向来模拟水流的流向。

3. 根据流向划分坡位等级。

流向法考虑了地形的水文特征，适用于水文模拟和水资源管理。

然而，流向法对地形数据的精度要求较高，且对水流的分布和路径有一定的假设。

五、斜度阈值法斜度阈值法是一种基于斜度阈值的坡位提取方法。

它通过设定斜度阈值来确定坡位。

具体步骤如下：1. 在地形数据上选择一个点P，计算该点的斜度。

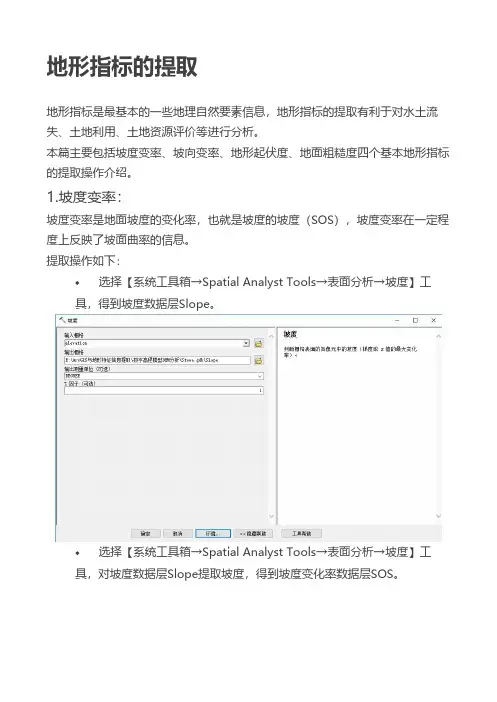
地形指标的提取地形指标是最基本的一些地理自然要素信息，地形指标的提取有利于对水土流失、土地利用、土地资源评价等进行分析。

本篇主要包括坡度变率、坡向变率、地形起伏度、地面粗糙度四个基本地形指标的提取操作介绍。

1.坡度变率：坡度变率是地面坡度的变化率，也就是坡度的坡度（SOS），坡度变率在一定程度上反映了坡面曲率的信息。

提取操作如下：选择【系统工具箱→Spatial Analyst Tools→表面分析→坡度】工具，得到坡度数据层Slope。

选择【系统工具箱→Spatial Analyst Tools→表面分析→坡度】工具，对坡度数据层Slope提取坡度，得到坡度变化率数据层SOS。

2.坡向变率：坡向变率是指在提取坡向数据的基础上提取坡向的变化率，也就是坡向之坡度（SOA），坡向变率可以很好地反映等高线的弯曲程度。

SOA在提取过程中在背面坡将会有误差产生（北面坡坡向值范围是0°90°和270°360°，在正北方向附近如15°~345°两个坡向差值只有30°，而计算结果却是330°），因此需要将北坡向的坡向变率进行误差纠正处理。

选择【系统工具箱→3D Analyst Tools→栅格表面→坡向】工具，提取原始DEM的坡向数据。

选择【系统工具箱→3D Analyst Tools→栅格表面→坡度】工具，提取上一步得到的坡向数据层的坡度数据，得到坡向变率数据层SOA1。

使用原始DEM中的最大值减去原始栅格，得到反地形DEM栅格图像。

然后依次选择【系统工具箱→3D Analyst Tools→栅格表面→坡向】工具和选择【系统工具箱→3D Analyst Tools→栅格表面→坡度】工具，得到坡向变率数据层SOA2。

选择【系统工具箱→Spatial Analyst Tools→地图代数→栅格计算器】工具，输入(("SOA_1" + "SOA_2") - Abs("SOA_1" - "SOA_2")) / 2地图代数公式，得到没有误差的DEM的坡向变率SOA。

arcgis基于dem的坡度提取原理ArcGIS基于DEM（数字高程模型）提取坡度的原理主要涉及对地面高程数据的分析。

以下是具体的原理和步骤：
1. 坡度计算：坡度是描述地面高程变化的一个指标，其计算是基于每一个栅格单元的高程变化率。

在DEM数据中，每一个栅格单元都有一个对应的高程值，通过计算相邻栅格单元之间的高程差，可以得到该栅格单元的坡度值。

2. 方向分析：除了坡度值，还可以分析地面的方向。

通过比较每一个栅格单元与其相邻栅格单元的高程差异，可以确定该栅格单元的坡向，即高程值最大的方向。

3. 提取坡度图层：基于DEM提取的坡度图层展示了地面的坡度分布情况。

坡度值越小，地势越平坦；坡度值越大，地势越陡峭。

这种图层对于地貌分析、水土流失研究、土地利用规划等应用具有重要的参考价值。

4. 动态更新：随着GIS数据的更新，相应的DEM和坡度图层也会进行动态更新，以反映最新的地形信息。

这种实时性对于自然灾害预警、土地利用变化监测等应用至关重要。

5. 与其他数据的集成：提取的坡度图层可以与其他类型的地理数据（如土地利用类型、水文数据等）进行集成，以进行更深入的综合分析。

总之，基于DEM提取坡度是利用地理信息系统（GIS）技术对数字高程数据进行处理和分析的一种方法，其原理主要基于高程变化率的计算和方向分析。

这种方法能够提供丰富的地形信息，对于多种应用领域具有重要意义。

地形坡度和坡向的计算公式一、坡度计算公式：1、百分比法表示坡度最为常用的方法，即两点高程差与其路程的百分比，其计算公式如下：坡度= (高程差/路程)x100%2、度数法用度数来表示坡度，利用反三角函数计算而得，其公式如下：tanα(坡度)= 高程差/路程二、角度计算公式角度和弧度关系是：2π弧度=360°。

从而1°≈0.0174533弧度，1弧度≈57.29578°。

1、角度转换为弧度公式：弧度=角度×(π÷180 )2、弧度转换为角度公式：角度=弧度×（180÷π）扩展资料依据国际地理学联合会地貌调查与地貌制图委员会关于地貌详图应用的坡地分类来划分坡度等级，规定：0°～0.5°为平原，>0.5°～2°为微斜坡，>2°～5°为缓斜坡，>5°～15°为斜坡，>15°～35°为陡坡，>35°～55°为峭坡，>55°～90°为垂直壁。

中国大陆规定>25°不能耕种。

西北黄土高原地区15°和25°分别为坡面流水面状侵蚀的下限和上限临界坡角。

在实际应用中，整数的角度已经够精准。

当需要更准确的角度值时，如天文学中量度星体或地球的经度和纬度，除了可用小数表示，还可以把角度细分为角分和角秒：1度为60分（60′），1分为60秒（60″）。

例如40.1875°= 40°11′15″。

要再准确一点的话，便用小数表示角秒，不再加设单位。

度为最常用的单位，其他单位与特定行业要求相关。

坡度和坡向变率引言在地理学和地形学领域，坡度和坡向变率是对地表特征进行定量描述和分析的重要指标。

它们对地貌发育、水文过程、土壤侵蚀等自然地理现象具有重要影响。

本文将从概念、计算方法、应用等方面对坡度和坡向变率进行全面探讨。

1. 坡度1.1 概念坡度是指地表某一点处沿着水平方向上单位距离纵向的变化量。

在地理学中，一般用百分比或角度来表示坡度。

百分比坡度是指垂直高度与水平距离的比值，可以用以下公式表示：百分比坡度 = (垂直高度/水平距离) × 100%角度坡度是指地表与水平面夹角的大小，常用度(°)作为单位。

1.2 计算方法计算坡度可以使用不同的方法，根据具体需求选择合适的计算公式。

一般情况下，可以采用以下两种常用的计算公式： 1. 垂直高度差法：将起点和终点的高程值相减，得到垂直高度差，然后除以水平距离。

百分比坡度 = (起点高程 - 终点高程) / 水平距离× 100%2.三角函数法：利用三角函数的定义，计算地表坡度。

角度坡度 = arctan[(起点高程 - 终点高程) / 水平距离]1.3 应用坡度是地貌发育和土地利用规划的重要参数之一。

具体应用场景如下： 1. 地貌分析：坡度能够帮助地貌学家分析山脉的地形特征、河流的梯度和侵蚀程度等。

2. 水文过程：坡度是水文模型中的重要输入参数，可以影响水文循环、径流形成和洪水过程等。

3. 土壤侵蚀：坡度是土壤侵蚀模型中的关键参数，对水土保持和防治水土流失起着重要作用。

2. 坡向变率2.1 概念坡向变率是指地表某一点处沿着地势方向上单位距离纵向的变化量。

它是一个表示地表倾斜程度和方向的指标。

常用度(°)作为单位。

2.2 计算方法计算坡向变率可以采用以下常用的方法： 1. 向量法：计算起点和终点的高程差，并根据方位角计算坡向。

坡向变率可以通过计算起点和终点的高程差除以水平距离得到。

坡向变率 = (起点高程 - 终点高程) / 水平距离2.GIS分析法：利用地理信息系统软件对高程数据进行处理和分析，得到坡向变率。

坡度计算公式范文坡度是指一个物体或地表倾斜的程度，通常以百分比或角度的形式表示。

在工程、地理和建筑等领域中，坡度计算是一个重要的问题，因为它可以帮助确定地势、测量地面倾斜度以及设计和施工阶段的要求。

坡度计算的公式取决于具体的应用场景。

下面将介绍一些常见的坡度计算公式：1.百分比坡度计算公式：地表坡度常以百分比的形式表示，表示为水平距离单位上升或下降的百分比。

百分比坡度计算公式如下：百分比坡度=(上升/水平距离)×1002.角度坡度计算公式：角度坡度是以度数表示的，是指地面斜率相对水平面的夹角。

角度坡度计算公式如下：角度坡度 = arctan(上升/水平距离)3.比例坡度计算公式：比例坡度是以比例的形式表示的，表示为单位水平距离所对应的垂直高度。

比例坡度计算公式如下：比例坡度=上升/水平距离需要注意的是，不同的坡度表示方法适用于不同的应用场景。

在工程设计中，通常使用百分比坡度或角度坡度，而在土方工程中，常用比例坡度。

此外，坡度计算还可以根据不同的地形和实际情况进行调整。

例如，如果地面有起伏或曲线，那么需要在计算中考虑这些因素。

通常，可以将地面分为多个小段，分别计算每个小段的坡度，然后求平均值来得到整个区域的坡度。

在实际应用中，还可以使用测量工具来测量坡度。

例如，在地理测量中，可以使用水准仪、全站仪等设备来测量地表的高程差，然后根据测量结果计算坡度。

总之，坡度计算是一个重要的工程问题，它可以帮助我们了解地表的倾斜情况和地势变化。

通过合适的坡度计算公式和测量工具，我们可以准确地计算坡度，并在设计和施工中合理地应用。

DEM坡面地形因子提取与分析DEM（数字高程模型）是一种数字化的地形模型，它包含了地球表面的高程信息，通常以栅格形式进行存储。

DEM数据的应用十分广泛，可以用于地形分析、水文建模、环境监测等领域。

在DEM数据的基础上，可以提取出各种地形因子，帮助人们了解地形特征、进行地形分析和模拟。

其中，DEM坡面地形因子是指在地形上特定位置上的坡度、坡向、坡长等地形指标。

这些地形因子对于水文模型、土壤侵蚀模拟、地质灾害预测等具有重要作用。

在本文中，将介绍DEM坡面地形因子的提取方法和分析过程。

一、DEM坡度的计算DEM坡度是地形上特定点的高程变化率，它反映了地形的陡缓程度。

坡度的计算可以通过计算升降高度差来得到。

通常采用以下公式来计算坡度：\[ \text{坡度} = \arctan(\sqrt((\Delta Z_x)^2+(\DeltaZ_y)^2)/\Delta d) \]其中，\( \Delta Z_x \)和\( \Delta Z_y \)分别是水平方向和竖直方向的高程差，\( \Delta d \)是间距。

二、DEM坡向的计算DEM坡向是指地形上特定点的最大坡度方向，即水平方向的方向角。

坡向的计算方法有多种，其中最常见的是通过计算水平和竖直高程差的比值，然后再根据不同情况进行角度的划分。

在此不做详细展开，需要根据具体情况选择适用的方法。

三、DEM坡长的计算DEM坡长是指地形上其中一点到邻近下游的最大距离，即沿坡度最大的路径所经过的距离，通常也是用来反映地形地势的陡缓程度。

坡长的计算可以通过得到每个像元到下游的距离，然后再计算像元之间的累计距离。

常见的计算方法有累积高程坡长和累积水平坡长，根据需要进行选择。

四、DEM地形曲率的计算地形曲率是指地形曲率的变化率，它反映了地形的凹凸程度。

地形曲率是坡度和坡向的综合表征，可以通过求取DEM的高程的二阶和二阶导数计算得到。

常见的方法有计算h-和v-曲率，分别表示水平和竖直方向的地形曲率。

(向下为y轴正方向，向右为x轴正方向)三阶反距离平方权差分[dz/dx] = ((c + 2f + i) - (a + 2d + g) / (8 *x_cell_size)[dz/dy] = ((g + 2h + i) - (a + 2b + c)) / (8 *y_cell_size)slope_radians = ATAN ( √ ( [dz/dx]2 + [dz/dy]2 ) )slope_degrees = A TAN ( √ ( [dz/dx]2 + [dz/dy]2 ) ) * 57.29578rise_run = √ ( [dz/dx]2 + [dz/dy]2 ]if aspect < 0cell = 90.0 - aspectelse if aspect > 90.0cell = 360.0 - aspect + 90.0elsecell = 90.0 - aspect1.加载ArcTutor>Spatial文件夹中的elevation；2.利用Spatial Analyst>Surface Analysis>Slope计算elevation数据的坡度，为避免求反正切函数，可选择Percent；3.利用Spatial Analyst>Surface Analysis>Aspect计算elevation数据的坡向；4.利用绘图工具在数据视图中画一包含3*3个像元的窗口，将其高程数据依次输入Excel中；5.按照坡度坡向的求取公式求坡度坡向；6.验证ArcGIS的坡度坡向求取算法。

坡度（Percent）=rise_run*100；aspect = 57.29578 * atan2 (-[dz/dx],[dz/dy])Erdas提取坡度坡向的算法(向上为y轴正方向，向右为x轴正方向)三阶不带权差分坡度的计算slope (in degrees) =坡度百分比所以坡度百分比为1~200。

坡度的计算方法
坡度是地形图中表示地物面升降程度的重要概念，它也是道路、河流、山脉和其他陆地物体在自然环境中形状表现的一个重要组成部分。

那么，坡度的计算方法又有哪些呢？
首先，计算坡度时需要考虑横截面图中各点相对于水平面的空间高度差和横向距离，一般来说，坡度就是横向距离与高度差之比。

具体来说，计算坡度的步骤如下：
（1）确定坡度的起点和终点，以及中间所经过的点；
（2）测量相应的横向距离，收集所有点之间的横向距离；
（3）计算相邻的两点之间的高度差，这些点可以是起点，终点
和中间所经过的点；
（4）计算坡度。

坡度的公式为：
坡度=Σ（高度差/横向距离）/点个数
经过上述步骤之后即可得出坡度的计算结果，坡度以“度”表示，一般在0.5°~90°之间，无高度差的表面的坡度等于0°，相对于水平面升高而非下降的水平面的坡度加上90度，这是求取坡度的基本
方法。

除了以上基本方法外，坡度还可以通过各种新技术和仪器来计算。

如此计算机辅助系统（Computer-Aided System），可以测量坡度并将其表示为平面图。

另外，还有一种叫做“激光测量仪”的精密仪器，它可以测量准确而快速地测量地形特性，比如坡度，它能够测量每一米的高度差，从而更加准确地计算坡度。

总之，坡度的计算方法有基本的计算方法和精密的仪器方法，它们都可以帮助我们更准确地计算出坡度。

在计算坡度时，是否使用基本的计算方法还是精密的仪器方法，取决于实际的调查任务，如果要做到精确，还需要考虑调查范围、探测距离等多种因素。

提取坡向变率（SOA）提取坡向变率1.背景:地面坡向变率是指坡向在水平方向上的变率,即地形表面一点扭曲变化程度的定量化因子在水平方向上的分量,它的提取方法为:在地表坡向提取基础上,对坡向变化率值的二次提取,亦即坡向之坡度(Slope of Aspect,SOA).在山区、丘陵地区地面坡向变率较大的值可以反映出地表的山脊线、山谷线。

2.数据：DEM栅格数据。

3.要求：为了得到纠正后的SOA，必须得到正地形SOA1和反地形SOA2，修正的公式为（（SOA1+SOA2）-Abs（SOA1-SOA2））/24.目标：通过实例，练习如何在模型中调用用户自定义的模型，明晰模型嵌套的过程。

5.操作步骤：本例中需要建立三个模型：生成SOA的模型、生成反地形的模型和纠正北坡误差的模型。

其中，前两个模型在最后一个模型中被调用。

（1）建立生成SOA模型1）打开ArcMAP启动ArcT oolBox2）右键单击ArcT oolBox，选择NewToolBox命令，生成toolbox23）右键单击toolbox2，在new命令中选择Model命令，生成model14）对建立的model1重命名为generate SOA5）在模型窗口中单击右键，选择CreateVariable命令，在数据类型选择对话框中选择Raster Layer，并将其名改为DEM6）打开SpatialAnalystTools的Surface工具集，分别将Aspect和Slope工具拖拽至模型生成器窗口中，并添加连接。

7）设置参数：（2）建立生成反地形的模型以类似的方法建立反地形模型，步骤如下：1）右键toolbox2，在new中选择model生成model22）在模型窗口右键，选择CreateVariable命令，在数据类型选择框中选中Rasterlayer，并改名为DEM3）加载SpatialAnlysttools|math|Trigonometric|minus和Abs 工具，并将其拖拽到模型生成器窗口中4）在ArcMap中打开DEM找出高程的最大值，将其设置为Input Raster or Constant，此例设置为4000，将outputraster（2）重命名为-DEM5）右键单击模型图标，选择属性命令，在Parameter内选择模型中用的参数DEM和-dem，点击模型界面上的保存图标，保存所有设置。