2012年全国中考数学试题分类解析汇编(159套63专题)专题34_命题与证明(附答案)

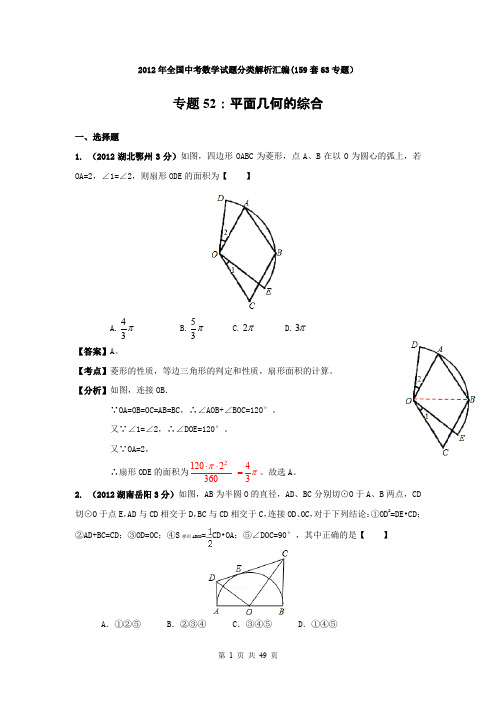
2012年全国中考数学试题分类解析汇编(159套63专题）专题52：平面几何的综合一、选择题1. （2012湖北鄂州3分）如图，四边形OABC 为菱形，点A 、B 在以O 为圆心的弧上，若OA=2，∠1=∠2，则扇形ODE 的面积为【 】A.π34B.π35C.π2D.π3【答案】A 。

【考点】菱形的性质，等边三角形的判定和性质，扇形面积的计算。

【分析】如图，连接OB ．∵OA=OB=OC=AB=BC，∴∠AOB+∠BOC=120°。

又∵∠1=∠2，∴∠DOE=120°。

又∵OA=2，∴扇形ODE 的面积为21202 4 3603ππ⋅⋅=。

故选A 。

2. （2012湖南岳阳3分）如图，AB 为半圆O 的直径，AD 、BC 分别切⊙O 于A 、B 两点，CD 切⊙O 于点E ，AD 与CD 相交于D ，BC 与CD 相交于C ，连接OD 、OC ，对于下列结论：①OD 2=DE•CD； ②AD+BC=CD；③OD=OC；④S 梯形ABCD =CD•OA；⑤∠DOC=90°，其中正确的是【 】A ．①②⑤ B．②③④ C．③④⑤ D．①④⑤【答案】A 。

【考点】切线的性质，切线长定理，相似三角形的判定与性质。

1052629【分析】如图，连接OE ，∵AD 与圆O 相切，DC 与圆O 相切，BC 与圆O 相切，∴∠DAO=∠DEO=∠OBC=90°，∴DA=DE，CE=CB ，AD∥BC。

∴CD=DE+EC=AD+BC。

结论②正确。

在Rt△ADO 和Rt△EDO 中，OD=OD ，DA=DE ，∴Rt△ADO≌Rt△EDO（HL ）∴∠AOD=∠EOD。

同理Rt△CEO≌Rt△CBO，∴∠EOC=∠BOC。

又∠AOD+∠DOE+∠EOC+∠COB=180°，∴2（∠DOE+∠EOC）=180°，即∠DOC=90°。

结论⑤正确。

∴∠DOC=∠DEO=90°。

2012年全国中考数学试题分类解析汇编159套63专题专题43：平行四边形一、选择题1. 2012广东佛山3分依次连接任意四边形各边的中点,得到一个特殊图形可认为是一般四边形的性质,则这个图形一定是A．平行四边形B．矩形C．菱形D．梯形答案 A;考点三角形中位线定理,平行四边形的判定;分析根据题意画出图形,如右图所示：连接AC,∵四边形ABCD各边中点是E、F、G、H,∴HG∥AC,HG=12AC,EF∥AC,EF=12AC;∴EF=GH,EF∥GH;∴四边形EFGH是平行四边形;由于四边形EFGH是平行四边形,它就不可能是梯形；同时由于是任意四边形,所以AC=BD或AC⊥BD不一定成立,从而得不到矩形或菱形的判断;故选A;2. 2012浙江杭州3分已知平行四边形ABCD中,∠B=4∠A,则∠C=A．18°B．36°C．72°D．144°答案B;考点平行四边形的性质,平行线的性质;分析由平行四边形性质求出∠C=∠A,BC∥AD,推出∠A+∠B=180°,求出∠A的度数,即可求出∠C：∵四边形ABCD是平行四边形,∴∠C=∠A,BC∥AD;∴∠A+∠B=180°;∵∠B=4∠A,∴∠A=36°;∴∠C=∠A=36°;故选B;3. 2012湖北武汉3分在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB＝5,BC＝6,则CE＋CF的值为A．11＋1132B．11－1132C ．11＋1132或11－1132D ．11－1132或1＋32答案C; 考点平行四边形的性质和面积,勾股定理;分析依题意,有如图的两种情况;设BE=x,DF=y;如图1,由AB ＝5,BE=x,得222AE AB BE 25x =-=-;由平行四边形ABCD 的面积为15,BC ＝6,得2625x =15-,解得53x=2±负数舍去; 由BC ＝6,DF=y,得222AF AD DF 36y =-=-;由平行四边形ABCD 的面积为15,AB ＝5,得2536y =15-,解得y=33±负数舍去;∴CE＋CF=6－532＋5－33=11－1132; 如图2,同理可得BE= 532,DF=33; ∴CE＋CF=6＋532＋5＋33=11＋1132; 故选C;4. 2012湖南益阳4分如图,点A 是直线l 外一点,在l 上取两点B 、C,分别以A 、C 为圆心,BC 、AB 长为半径画弧,两弧交于点D,分别连接AB 、AD 、CD,则四边形ABCD 一定是A ．平行四边形B ．矩形C ．菱形D ．梯形答案A;考点作图复杂作图,平行四边形的判定;分析∵别以A 、C 为圆心,BC 、AB 长为半径画弧,两弧交于点D,∴AD=BC,AB=CD;∴四边形ABCD 是平行四边形两组对边分别相等的四边形是平行四边形;故选A;5. 2012四川广元3分 若以A,0,B2,0,C0,1三点为顶点要画平行四边形,则第四个顶点不可能在A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案C;考点平行四边形的判定,坐标与图形性质;分析根据题意画出图形,如图所示：分三种情况考虑：①以CB 为对角线作平行四边形ABD 1C,此时第四个顶点D 1落在第一象限；②以AC 为对角线作平行四边形ABCD 2,此时第四个顶点D 2落在第二象限；③以AB 为对角线作平行四边形ACBD 3,此时第四个顶点D 3落在第四象限;则第四个顶点不可能落在第三象限;故选C;6. 2012四川德阳3分 如图,点D 是△ABC 的边AB 的延长线上一点,点F 是边BC 上的一个动点不与点B 重合.以BD 、BF 为邻边作平行四边形BDEF,又AP BE 点P 、E 在直线AB 的同侧,如果BD B 14A =,那么△PBC 的面积与△ABC 面积之比为A.41B.53C.51D.43 答案D;考点平行四边形的判定和性质;分析过点P 作PH∥BC 交AB 于H,连接CH,PF,PE;∵APBE,∴四边形APEB 是平行四边形;∴PE AB;, ∵四边形BDEF 是平行四边形,∴EFBD; ∴EF∥AB;∴P,E,F 共线;设BD=a,∵1BD AB 4=,∴PE=AB=4a;∴PF=PE﹣EF=3a; ∵PH∥BC,∴S △HBC =S △PBC ;∵PF∥AB,∴四边形BFPH 是平行四边形;∴BH=PF=3a;∵S △HBC ：S △ABC =BH ：AB=3a ：4a=3：4,∴S △PBC ：S △ABC =3：4;故选D;7. 2012四川巴中3分不能判定一个四边形是平行四边形的条件是A. 两组对边分别平行B. 一组对边平行,另一组对边相等C. 一组对边平行且相等D. 两组对边分别相等答案B;考点平行四边形的判定分析根据平行四边形的判定：①两组对边分别平行的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③两组对角分别相等的四边形是平行四边形；④对角线互相平分的四边形是平行四边形；⑤一组对边平行且相等的四边形是平行四边形; A、D、C均符合是平行四边形的条件,B则不能判定是平行四边形;故选B;8. 2012四川自贡3分如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为A．2和3 B．3和2 C．4和1 D．1和4 答案B;考点平行四边形的性质,平行的性质,等腰三角形的判定和性质;分析∵AE平分∠BAD,∴∠BAE=∠DAE;∵四边形ABCD是平行四边形,∴AD∥BC;∴∠DAE=∠AEB;∴∠BAE=∠BEA;∴AB=BE=3;∴EC=AD﹣BE=2;故选B;答案D;考点平行四边形的性质,平行的性质,等腰三角形的判定;分析∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,AD=BC;∴∠AEB=∠E BC;又BE平分∠ABC,∴∠ABE=∠EBC;∴∠ABE=∠AEB;∴AB=AE;同理可得：DC=DF;∴AE=DF;∴AE－EF=DE－EF,即AF=DE;当1EF AD4=时,设EF=x,则AD=BC=4x;∴AF=DE=14AD－EF=;∴AE=AB=AF+EF=;∴AB：BC=：4=5：8;∵以上各步可逆,∴当AB：BC=：4=5：8时,1EF AD4=;故选D;10. 2012山东聊城3分如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是A．DF=BE B．AF=CE C．CF=AE D．CF∥AE答案C;考点平行四边形的性质,全等三角形的判定;分析根据平行四边形的性质和全等三角形的判定方法逐项分析即可：A、当DF=BE时,由平行四边形的性质可得：AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE；B、当AF=CE时,由平行四边形的性质可得：BE=DF,AB=CD,∠B=∠D,利用SAS可判定△CDF≌△ABE；C、当CF=AE时,由平行四边形的性质可得：AB=CD,∠B=∠D,利用SSA不能可判定△CDF≌△ABE；D、当CF∥AE时,由平行四边形的性质可得：AB=CD,∠B=∠D,∠AEB=∠CFD,利用AAS可判定△CDF≌△ABE;故选C;11. 2012山东泰安3分如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=53°,则∠BCE的度数为A．53°B．37°C．47°D．123°答案B;考点平行四边形的性质,对项角的性质,平行的性质;分析设CE与AD相交于点F;∵在平行四边形ABCD中,过点C的直线CE⊥AB,∴∠E=90°,∵∠EAD=53°,∴∠EFA=90°﹣53°=37°;∴∠DFC=37∵四边形ABCD是平行四边形, ∴AD∥BC;∴∠BCE=∠DFC=37°;故选B;12. 2012广西南宁3分如图,在平行四边形ABCD中,AB=3cm,BC=5cm,对角线AC,BD相交于点O,则OA的取值范围是A．2cm＜OA＜5cm B．2cm＜OA＜8cm C．1cm＜OA＜4cm D．3cm＜OA＜8cm答案C;考点平行四边形的性质,三角形三边关系;分析∵平行四边形ABCD 中,AB=3cm,BC=5cm, ∴OA=OC=12AC 平行四边形对角线互相平分, BC －AB ＜AC ＜BC ＋AB 三角形三边关系,即2cm ＜AC ＜8cm;∴1cm＜OA ＜4cm;故选C;13. 2012内蒙古包头3分如图,过口ABCD 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与GH ,那么图中的口AEMG 的面积S 1 与口HCFG 的面积S 2的大小关系是A .S 1 > S 2 < S 2 C .S 1 = S 2 = S 2答案C;考点平行四边形的判定和性质;分析易知,四边形BHME 和MFDG 都是平行四边形;∵平行四边形的对角线把平行四边形分成了两个面积相等的三角形,∴ABD BCD EBM BHM GMD DMF S S S S S S ∆∆∆∆∆∆===，，;∴ABD EBM GMD BCD BHM DMF S S S S S S ∆∆∆∆∆∆--=--,即S 1 = S 2;故选C;14. 2012黑龙江绥化3分如图,在平行四边形ABCD 中,E 是CD 上的一点,DE ：EC=2：3,连接AE 、BE 、BD,且AE 、BD 交于点F,则S △DEF ：S △EBF ：S △ABF =A ．2：5：25B ．4：9：25C ．2： 3：5D ．4：10：25答案D;考点平行四边形的性质,相似三角形的判定和性质;分析由DE ：EC=2：3得DE ：DC=2：5,根据平行四边形对边相等的性质,得DE ：AB=2：5 由平行四边形对边平行的性质易得△DFE∽△BFA∴DF：FB= DE ：AB=2：5,S △DEF ：S △ABF =4：25;又∵S △DEF 和S △EBF 是等高三角形,且DF ：FB =2：5,∴S △DEF ：S △EBF =2：5=4：10;∴S △DEF ：S △EBF ：S △ABF =4：10：25;故选D;二、填空题1. 2012广东汕头4分如图,在 ABCD 中,AD=2,AB=4,∠A=30°,以点A 为圆心,AD 的长为半径画弧交AB 于点E,连接CE,则阴影部分的面积是 ▲ 结果保留π．答案133π-;考点平行四边形的性质,扇形面积的计算分析过D点作DF⊥AB于点F;∵AD=2,AB=4,∠A=30°,∴DF=AD sin30°=1,EB=AB﹣AE=2;∴阴影部分的面积=平行四边形ABCD的面积－扇形ADE面积－三角形CBE的面积=230211 4121336023ππ⨯⨯⨯--⨯⨯=-;2. 2012浙江衢州4分如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,CD=2DE．若△DEF的面积为a,则平行四边形ABCD的面积为▲ 用a的代数式表示．答案12a;考点平行四边形的性质,相似三角形的判定和性质;分析∵四边形ABCD是平行四边形,∴AB∥CD,AD∥BC,AB=CD,∴△DEF∽△CEB,△DEF∽△ABF;∴S△DEF：S△CE B=DE：CE2,S△DEF：S△ABF=DE：AB2,∵CD=2DE,∴DE：CE=1：3,DE：AB=1：2,∵S△DEF=a,∴S△CBE=9a,S△ABF=4a,∴S四边形BCDF=S△CEB﹣S△DEF=8a;∴S ABCD=S四边形BCDF+S△ABF=8a+4a=12a;3. 2012江苏南京2分如图,在平行四边形ABCD中,AD=10cm,CD=6cm,E为AD上一点,且BE=BC,CE=CD,则DE= ▲ cm答案;考点平行四边形的性质,平行的性质,等腰三角形的性质,相似三角形的判定和性质;分析∵四边形ABCD是平行四边形,AD=10cm,CD=5cm,∴BC=AD=10cm,AD∥BC,∴∠2=∠3;∵BE=BC,CE=CD,∴BE=BC=10cm,CE=CD=5cm,∠1=∠2,∠3=∠D;∴∠1=∠2=∠3=∠D;∴△BCE∽△CDE;∴BC CECD DE=,即1055DE=,解得DE=;4. 2012江苏镇江2分如图,E是平行四边形ABCD的边CD上一点,连接AE并延长交BC的延长线于点F,且AD=4,CE1AB3=,则CF的长为▲ ;答案2;考点平行四边形的性质,相似三角形的判定和性质的;分析∵四边形ABCD 是平行四边形,∴AB∥DC,BC=AD=4;∴△CEF∽△ABF;∴CE CF AB BF =; 又∵CE 1AB 3=,BF=BC+CF=4+ CF,∴CF 14CF 3=+,解得CF=2; 5. 2012湖北鄂州3分如图,ABCD 中,AE⊥BC 于E,AF⊥CD 于F,若AE=4,AF=6,sin∠BAE=31,则CF= ▲ .考点平行四边形的性质,锐角三角函数定义,勾股定理,相似三角形的判定和性质;分析由AE⊥BC 和sin∠BAE=13,得BE 1AB 3=;∴可设BE=k,则AB=3k;∵AE=4,∴根据勾股定理得222AB AE BE =+,即()2223k 4k =+,解得;;∵四边形ABCD ,∠D=∠B;又∵AE⊥BC,AF⊥CD,∴∠AFD=∠AEB=900;∴△AFD∽△AEB;∴DF AF BE AE=;64=,解得DF DF= =6. 2012湖南永州3分如图,平行四边形ABCD 的对角线相交于点O,且AB≠AD,过O 作OE⊥BD 交BC 于点E ．若△CDE 的周长为10,则平行四边形ABCD 的周长为 ▲ ．答案20;考点平行四边形的性质,线段垂直平分线的性质;144482分析∵四边形ABCD 是平行四边形,∴OB=OD,AB=CD,AD=BC 平行四边形对边相等,对角线互相平分;∵OE⊥BD,∴BE=DE 线段垂直平分线上的点到线段两端的距离相等;∵△CDE 的周长为10,即CD+DE+EC=10,∴平行四边形ABCD 的周长为：AB+BC+CD+AD=2BC+CD=2BE+EC+CD=2DE+EC+CD=2×10=20;7. 2012湖南怀化3分如图,在ABCD 中,AD=8,点E 、F 分别是BD 、CD 的中点,则EF=▲ .答案4;考点平行四边形的性质,三角形中位线定理;分析∵四边形ABCD 是平行四边形,∴BC=AD=8;∵点E 、F 分别是BD 、CD 的中点,∴EF=12BC=12×8=4; 8. 2012湖南湘潭3分如图,在ABCD 中,点E 在DC 上,若EC ：AB=2：3,EF=4,则BF=▲ ． 答案6;考点平行四边形的性质,相似三角形的判定和性质;分析∵四边形ABCD 是平行四边形,∴AB∥CD;∴∠CAB=∠ACD,∠ABE=∠BEC; ∴△ABF∽△CEF;∴AB BF CE EF=, 又∵EC：AB=2：3, EF=4,∴3BF 24=,解得BF=6; 9. 2012四川成都4分如图,将ABCD 的一边BC 延长至E,若∠A=110°,则∠1= ▲ ．答案70°;考点平行四边形的性质,平角的性质; 分析∵平行四边形ABCD 的∠A=110°,∴∠BCD=∠A=110°;∴∠1=180°﹣∠BCD=180°﹣110°=70°;10. 2012辽宁本溪3分如图,在□ABCD 中,∠ABC 的平分线BE 交AD 边于点E,交对角线AC 于点F,若AB 3BC 5=,则AF AC = ▲ ; 答案38; 考点平行四边形的性质,平行的性质,相似三角形的判定和性质;分析∵四边形ABCD 是平行四边形,∴AD∥BC,∠EBC=∠AEB;∵BE 是∠ABC 的角平分线,∴∠EBC=∠AEB=∠ABE,AB=AE; ∵AB 3BC 5=,∴AE 3BC 5=; ∵AD∥BC,∴△AFE∽△CFB;∴AE AF 3BC FC 5==;∴AF 3AF FC 8=+;∴AF 3AC 8=; 11. 2012贵州黔西南3分如图,在△ABC 中,∠ACB＝90°,D 是BC 的中点,DE⊥BC,CE2012山东烟台3分ABCD中,已知点A﹣1,0,B2,0,D0,1．则点C的坐标为▲ ．答案3,1;考点平行四边形的性质,坐标与图形性质;分析画出图形,根据平行四边形性质求出DC∥AB,DC=AB=3,根据D的纵坐标和CD=3即可求出答案：∵平行四边形ABCD中,已知点A﹣1,0,B2,0,D0,1,∴AB=CD=2﹣﹣1=3,DC∥AB;∴C的横坐标是3,纵坐标和D的纵坐标相等,是1;∴C的坐标是3,1;13. 2012吉林长春3分如图,ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合．若△ACD的面积为3,则图中的阴影部分两个三角形的面积和为▲ .答案3;考点平行四边形和矩形的性质;分析∵四边形ABCD是平行四边形,∴△ACD的面积=△ACB的面积;又∵△ACD的面积为3,∴△ACB的面积为3;∵△ACB的面积矩形AEFC的面积的一半, ∴阴影部分两个三角形的面积和=△ACB的面积=3; 14. 2012黑龙江龙东地区3分如图,在平行四边形ABCD中,点E、F分别在边BC、AD上,请添加一个条件使四边形AECF是平行四边形只填一个即可;答案AF=CE答案不唯一;考点平行四边形的判定和性质;分析根据平行四边形性质得出AD∥BC,AF=CE,得出AF∥CE;根据有一组对边相等且平行的四边形是平行四边形的判定,可添加AF=CE 或FD=EB;根据两组对边分别平行的四边形是平行四边形的定义,可添加AE∥FC;添加∠AEC=∠FCA 或∠DAE=∠DFC 等得到AE∥FC,也可使四边形AECF 是平行四边形;三、解答题1. 2012北京市5分已知：如图,点E,A,C 在同一条直线上,AB∥CD,AB=CE,AC=CD．求证：BC=ED.答案证明：∵AB∥CD,∴∠BAC=∠ECD,∵在△BAC 和△E CD 中,AB=EC,∠BAC=∠ECD ,AC=CD,∴△BAC≌△ECDSAS;∴CB=ED;考点平行线的性质,全等三角形的判定和性质;分析首先由AB∥CD,根据平行线的性质可得∠BAC=∠ECD,再由条件AB=CE,AC=CD 可证出△BAC 和△ECD 全等,再根据全等三角形对应边相等证出CB=ED;2. 2012陕西省6分如图,在ABCD 中,∠ABC 的平分线BF 分别与AC 、AD 交于点E 、F ．1求证：AB=AF ；2当AB=3,BC=5时,求AE AC 的值． 答案解：1证明：如图,在ABCD 中,AD∥BC, ∴∠2=∠3;∵BF 是∠ABC 的平分线,∴∠1=∠2;∴∠1=∠3;∴AB=AF;2∵AEF CEB 23∠=∠∠=∠，,∴△AEF∽△CEB;∴AE AF 3EC BC 5==, ∴AE 3AC 8=; 考点平行四边形的性质,平行线的性质,等腰三角形的判定,相似三角形的判定和性质;分析1由在ABCD 中,AD∥BC,利用平行线的性质,可求得∠2=∠3,又由BF 是∠ABC 的平分线,易证得∠1=∠3,利用等角对等边的知识,即可证得AB=AF;2易证得△AEF∽△CEB,利用相似三角形的对应边成比例,即可求得AE AC的值; 3. 2012广东省6分已知：如图,在四边形ABCD 中,AB∥CD,对角线AC 、BD 相交于点O,BO=DO ． 求证：四边形ABCD 是平行四边形．答案证明：∵AB∥CD,∴∠ABO=∠CDO,在△ABO 与△CDO 中,∵∠ABO=∠CDO,BO=DO,∠AOB=∠COD,∴△ABO≌△CDOASA;∴AB=CD;∴四边形ABCD是平行四边形;考点平行的性质,全等三角形的判定和性质,平行四边形的判定;分析根据AB∥CD可知∠ABO=∠CDO,再由BO=DO,∠AOB=∠COD,即可根据ASA得出△ABO≌△CDO,故可得出AB=CD,从而根据一组对边平行且相等的四边是平行四边形的判定得出结论;4. 2012广东湛江8分如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF．求证：1△ABE≌△CDF；2四边形BFDE是平行四边形．答案证明：1∵四边形ABCD是平行四边形,∴∠A=∠C,AB=CD,在△ABE和△CDF中,∵AB=CD,∠A=∠C,AE=CF,∴△ABE≌△CD FSAS;2∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC;∵AE=CF,∴AD﹣AE=BC﹣CF,即DE=BF;∴四边形BFDE是平行四边形;考点平行四边形的性质和判定,全等三角形的判定;分析1由四边形ABCD是平行四边形,根据平行四边形的对边相等,对角相等的性质,即可证得∠A=∠C,AB=CD,又由AE=CF,利用SAS,即可判定△ABE≌△CDF;2由四边形ABCD是平行四边形,根据平行四边形对边平行且相等,即可得AD∥BC,AD=BC,又由AE=CF,即可证得DE=BF;根据对边平行且相等的四边形是平行四边形,即可证得四边形BFDE是平行四边形;5. 2012浙江湖州8分已知：如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E．1说明△DCE≌△FBE的理由；2若EC=3,求AD的长．答案1证明：∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC;∴∠CDE=∠F;又∵BF=AB,∴DC=FB;在△DCE和△FBE中,∵ ∠CDE=∠F,∠CED=∠BEF, DC=FB,∴△DCE≌△FBEAAS;2解：∵△DCE≌△FBE,∴EB=EC;∵EC=3,∴BC=2EB=6;∵四边形ABCD是平行四边形,∴AD=BC;∴AD=6;考点平行四边形的性质,平行的性质,全等三角形的判定和性质;分析1由四边形ABCD是平行四边形,根据平行四边形的对边平行且相等,即可得AB=DC,AB∥DC,继而可求得∠CDE=∠F,又由BF=AB,即可利用AAS,判定△DCE≌△FBE;2由1,可得BE=EC,即可求得BC的长,又由平行四边形的对边相等,即可求得AD的长;6. 2012浙江衢州6分如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BE=DF,连接AE、CF．请你猜想：AE与CF有怎样的数量关系并对你的猜想加以证明．答案解：猜想：AE=CF;证明如下：∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD;∴∠ABE=∠CDF;在△ABE和△CDF中,AB=CD,∠ABE=∠CDF,BE=DF,∴△ABE≌△CDFSAS,∴AE=CF;考点平行四边形的性质,平行线的性质,全等三角形的判定和性质; 分析由四边形ABCD是平行四边形,即可得AB∥CD,AB=CD,然后利用平行线的性质,求得∠ABE=∠CDF,又由BE=DF,即可由SAS证得△ABE≌△CDF,从而可得AE=CF;7. 2012江苏淮安8分已知：如图在平行四边形ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F;求证：△BEF≌△CDF答案证明：∵四边形ABCD是平行四边形,∴DC∥AB,DC=AB; ∴∠CDF=∠B,∠C=∠FBE;又∵BE=AB,∴BE=CD;∵在△BEF和△CDF中,∠CDF=∠B,BE=CD,∠C=∠FBE,∴△BEF≌△CDFASA;考点平行四边形的性质,平行的性质,全等三角形的判定;分析根据平行四边形的对边平行且相等可得AB=CD,AB∥CD,再根据两直线平行,内错角相等可得∠C=∠FBE,然后利用ASA证明即可;8. 2012江苏泰州10分如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF．求证：四边形ABCD是平行四边形．答案证明：∵AE⊥AD,CF⊥BC,∴∠EAD=∠CFB=90°;∵AE∥CF,∴∠AED=∠CFB;在Rt△AED和Rt△CFB中,∵∠EAD=∠CFB=90°,∠AED=∠CFB, AE=CF,∴Rt△AED≌Rt△CFBASA;∴AD=BC;又∵AD∥BC,∴四边形ABCD是平行四边形;考点平行的性质,全等三角形的判定和性质,平行四边形的判定;分析由垂直得到∠EAD=∠BCF=90°,根据AAS可证明Rt△AED≌Rt△CFB,得到AD=BC,根据平行四边形的判定判断即可;9. 2012江苏无锡8分如图,在ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF．求证：∠BAE=∠CDF．答案证明：∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC;∴∠B=∠DCF;∵在△ABE和△DCF中,AB=DC,∠B=∠DCF,BE=CF,∴△ABE≌△DCFSAS;∴∠BAE=∠CDF;考点平行四边形的性质,平行的性质,全等三角形的判定和性质;分析根据平行四边形的性质可得AB=DC,AB∥DC,再根据平行线的性质可得∠B=∠DCF,即可由SAS证明△ABE≌△DCF,再根据全等三角形对应边相等的性质得到结论;10. 2012江苏徐州6分如图,C为AB的中点;四边形ACDE为平行四边形,BE与CD相交于点F;求证：EF=BF;答案证明：∵四边形ACDE为平行四边形,∴ED=AC,ED∥AC;∴∠D=∠FCB,∠DEF=∠B;又∵C为AB的中点,∴AC=BC;∴ED=BC;在△DEF和△C BF中,∵∠D=∠FCB,ED=BC,∠DEF=∠B,∴△DEF≌△CBFSAS;∴EF=BF;考点平行四边形的性质,平行的性质,全等三角形的判定和性质;分析根据平行四边形对边平行且相等的性质,易用SAS证明△DEF≌△CBF,从而根据全等三角形对应边相等的性质即可证得EF=BF;11. 2012福建厦门10分已知ABCD,对角线AC与BD相交于点O,点P在边AD上,过点P分别作PE⊥AC、PF⊥BD,垂足分别为E、F,PE＝PF．1如图,若PE＝错误!,EO＝1,求∠EPF的度数；2若点P是AD的中点,点F是DO的中点,BF ＝BC＋3错误!－4,求BC的长．答案解：1连接PO ,∵ PE＝PF,PO＝PO,PE⊥AC、PF⊥BD,∴ Rt△PEO≌Rt△PFOHL;∴∠EPO＝∠FPO;在Rt△PEO中, tan∠EPO＝错误!＝错误!,∴ ∠EPO＝30°;∴ ∠EPF＝60°;2∵点P是AD的中点,∴ AP＝DP;又∵ PE＝PF,∴ Rt△PEA≌Rt△PFDHL;∴∠OAD＝∠ODA;∴ OA＝OD;∴ AC＝2OA＝2OD＝BD;∴ABCD是矩形;∵ 点P是AD的中点,点F是DO的中点,∴ AO∥PF;∵ PF⊥BD,∴ AC⊥BD;∴ABCD是菱形;∴ABCD是正方形;∴ BD＝错误!BC;∵ BF＝错误!BD,∴BC＋3错误!－4＝错误!BC,解得,BC＝4;考点平行四边形的性质,角平分线的性质,三角形中位线定理,全等三角形的判定和性质,正方形的判定和性质,锐角三角函数定义;分析1连接PO,利用解直角三角形求出∠EPO=30°,再利用“HL”证明△PEO和△PFO全等,根据全等三角形对应角相等可得∠FPO=∠EPO,从而得解;2根据条件证出 ABCD是正方形;根据正方形的对角线与边长的关系列式计算即可得解; 12. 2012福建莆田8分如图,四边形ABCD是平行四边形,连接AC．14分请根据以下语句画图,并标上相应的字母用黑色字迹的钢笔或签字笔画．①过点A画AE⊥BC于点E；②过点C画CF∥AE,交AD于点F；24分在完成1后的图形中不再添加其它线段和字母,请你找出一对全等三角形,并予以证明．答案解：1画图如下：2△ABC≌△CDA ;证明如下：∵ 四边形ABCD是平行四边形,∴ AB＝CD,BC＝DA;又∵ AC＝CA,∴△ABC≌△CDASSS;考点作图复杂作图,平行四边形的性质,全等三角形的判定;分析1根据语句要求画图即可;2首先根据平行四边形的性质和AE∥CF,可得①△ABC≌△CDA,②△AEC≌△CFA,③△ABE≌△CDF;下面给出其它两个的证明：②△AEC≌△CFA;证明如下：∵四边形ABCD是平行四边形,∴ AD∥BC;∴ ∠DAC＝∠ACE;∵AE∥CF,∴ ∠EAC＝∠ACF;∵AC=CA,∴ △AEC≌△CFAASA;③△ABE≌△CDF;证明如下：∵四边形ABCD是平行四边形,∴ AD∥BC,∠B＝∠D,AB ＝CD ;又∵AE∥CF,∴四边形AECF是平行四边形;∴∠AEC＝∠AFC;∴∠AEB＝∠CFD;∴△ABE≌△CDFAAS;13. 2012福建南平8分如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,请再从下列三个备选条件中,选择添加一个恰当的条件．使四边形AECF是平行四边形,并予以证明, 备选条件：AE=CF,BE=DF,∠AEB=∠CFD,我选择添加的条件是：注意：请根据所选择的条件在答题卡相应试题的图中,画出符合要求的示意图,并加以证明答案解：添加的条件可以是BE=DF答案不唯一;证明如下：∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC;∵BE=DF,∴AF=CE,即AF=CE,AF∥CE;∴四边形AECF是平行四边形;考点平行四边形的判定和性质,全等三角形的判定和性质,平行的判定和性质;分析根据平行四边形性质得出AD∥BC,AD=BC,求出AF∥CE,AF=CE,根据平行四边形的判定推出即可;当AE=CF时,四边形AECF可能是平行四边形,也可能是等腰梯形;当∠AEB=∠CFD时,四边形AECF也是平行四边形,证明如下：∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D;∵∠AEB=∠CFD,∴△AEB≌△CFDAAS;∴AE=CF;∵四边形ABCD是平行四边形,∴AD∥BC;∴∠AEB=∠EAF;∴∠CFD=∠EAF;∴AE∥FC;∴四边形AECF是平行四边形;14. 2012福建泉州9分如图,BD是平行四边形ABCD的一条对角线,AE⊥BD于点E,CF⊥BD于点F,求证∠DAE=∠BCF.答案证明：证明：∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC平行四边形对边平行且相等∴∠ADB=∠CBD两直线平行,内错角相等;∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB=90°垂直的定义;在△ADE和△CBF中,∵∠ADB=∠CBD,∠AED=∠CFB,AD=CB,∴△ADE≌S△CBFAAS;∴∠DAE=∠BCF全等三角形的对应角相等;考点平行四边形的性质,平行的性质,全等三角形的判定和性质;分析由四边形ABCD为平行四边形,根据平行四边形的对边平行且相等得到AD=BC,AD与BC平行,利用两直线平行内错角相等得到一对角相等,再由AE⊥BD,CF⊥BD得到一对直角相等,利用AAS可得出三角形ADE与三角形CBF全等,利用全等三角形的对应角相等可得出∠DAE=∠BCF,得证;15. 2012湖北黄石7分如图,已知在平行四边形ABCD中,BE=DF.求证：∠DAE=∠BCF.答案证明：∵四边形ABCD为平行四边形, ∴AD∥BC,且AD=BC;∴∠ADE=∠BCF;又∵BE=DF, ∴BF=DE;∴△ADE≌△CBFSAS;∴∠DAE=∠BCF ;考点平行四边形的性质,平行线的性质,全等三角形的判定和性质;分析根据平行四边形性质求出AD∥BC,且AD=BC,推出∠ADE=∠CBF,求出DE=BF,由SAS证△ADE≌△CBF,推出∠DAE=∠BCF即可;16. 2012湖南郴州8分已知：点P是ABCD的对角线AC的中点,经过点P的直线EF交AB于点E,交DC 于点F．求证：AE=CF．答案证明：∵四边形ABCD是平行四边形,∴AB∥CD,∴∠PAE=∠PCF;∵点P是ABCD的对角线AC的中点,∴PA=PC;在△PAE和△PCE中,∵∠PAE=∠PCF,PA=PC,∠APE=∠CPF,∴△PAE≌△PCEASA;∴AE=CF;考点平行四边形的性质,全等三角形的判定和性质;分析由四边形ABCD是平行四边形,易得∠PAE=∠PCF,由点P是 ABCD 的对角线AC的中点,可得PA=PC,又由对顶角相等,可得∠APE=∠CPF,即可利用ASA证得△PAE≌△PCF,即可证得AE=CF;17. 2012四川广安6分如图,四边形ABCD是平行四边形,点E在BA的延长线上,且BE=AD,点F在AD上,AF=AB,求证：△AEF≌△DFC．答案证明：∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD; ∴∠D=∠EAF;∵AF=AB,BE=AD,∴AF=CD,AD﹣AF=BE﹣AB,即DF=AE;在△AEF和△DFC中,∵AE=DF,∠EAF=∠D,AF=DC,∴△AEF≌△DFCSAS,考点平行四边形的性质,平行线的性质,全等三角形的判定;分析由四边形ABCD是平行四边形,利用平行四边形的性质,即可得AB=CD,AB∥CD,又由平行线的性质,即可得∠D=∠EAF,然后由BE=AD,AF=AB,求得AF=CD,DF=AE,从而由SAS证得;18. 2012辽宁鞍山8分如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP．求证：FP=EP．答案证明：∵四边形ABCD是平行四边形,∴AD∥BC;∴∠DGC=∠GCB,∵DG=DC,∴∠DGC=∠DCG;∴∠DCG=∠GCB;∵∠DCG+∠DCP=180°,∠GCB+∠FCP=180°,∴∠DCP=∠FCP;∵在△PCF和△PCE中,CE=CF,∠FCP=∠ECP,CP=CP,∴△PCF≌△PCESAS;∴PF=PE;考点平行四边形的性质,平行的性质,等腰三角形的性质,全等三角形的判定和性质;分析根据平行四边形的性质推出∠DGC=∠GCB,根据等腰三角形性质求出∠DGC=∠DCG,推出∠DCG=∠GCB,根据等角的补角相等求出∠DCP=∠FCP,根据SAS证出△PCF≌△PCE即可;19. 2012辽宁大连9分如图,□ABCD中,点E、F分别在AD、BC上,且ED＝BF,EF与AC相交于点O.求证：OA＝OC.答案证明：∵四边形ABCD是平行四边形,∴AD=BC;∵ED＝BF,∴AE=CF;∵四边形ABCD是平行四边形,∴AD∥BC;∴∠OAE=∠OCF,∠OEA=∠OFC;在△AOE 和△COF中,∵∠OAE=∠OCF,AE=CF,∠OEA=∠OFC,∴△AOE ≌△COFASA;∴OA＝OC;考点平行四边形的性质,平行的性质,全等三角形的判定和性质;分析根据平行四边形的性质可得AD BC;由等量减等量差相等得AE=CF；由两直线平行内错角相等得∠OAE=∠OCF,∠OEA=∠OFC;由ASA证得△AOE ≌△COF,从而根据全等三角形对应边相等的性质得OA＝OC;20. 2012辽宁沈阳10分已知,如图,在荀ABCD中,延长DA到点E,延长BC到点F,使得AE＝CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.1求证：△AEM≌△CFN；21世纪教育网2求证：四边形BMDN是平行四边形.答案证明：1 ∵四边形ABCD是平行四边形,∴AB∥DC ,AD∥BC;∴∠E=∠F,∠DAB=∠BCD; ∴∠EAM=∠FCN;又∵AE=CF ∴△AEM≌△CFNASA;2 ∵由1△AEM≌△CFN, ∴AM=CN;又∵四边形ABCD是平行四边形,∴AB CD ;∴BM DN;∴四边形BMDN是平行四边形;考点平行四边形的判定和性质,平行的性质,全等三角形的判定和性质;分析1根据平行四边形的性质可得出AD∥BC,∠DAB=∠BCD,再根据平行线的性质及补角的性质得出∠E=∠F,∠EAM=∠FCN,从而利用ASA可作出证明;2根据平行四边形的性质及1的结论可得BM DN,则由有一组对边平行且相等的四边形是平行四边形即可证明;21. 2012贵州六盘水12分如图,已知E是 ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F．1求证：△ABE≌△FCE．2连接AC．BF,若∠AEC=2∠ABC,求证：四边形ABFC为矩形．答案证明：1∵四边形ABCD为平行四边形,∴AB∥DC;∴∠ABE=∠ECF;又∵E为BC的中点,∴BE=CE;在△ABE和△FCE中,∵∠ABE=∠FCE,BE=CE,∠AEB=∠FEC,∴△ABE≌△FCEASA;2∵△ABE≌△FCE,∴AB=CF;又AB∥CF,∴四边形ABFC为平行四边形;∴BE=EC,AE=EF;又∵∠AEC=2∠ABC,且∠AEC为△ABE的外角,∴∠AEC=∠ABC+∠EAB;∴∠ABC=∠EAB,∴AE=BE;∴AE+EF=BE+EC,即AF=BC;∴四边形ABFC为矩形;考点平行四边形的性质,平行的性质,全等三角形的判定和性质,等腰三角形和判定,矩形的判定;分析1由ABCD为平行四边形,根据平行四边形的对边平行得到AB与DC平行,根据两直线平行内错角相等得到一对角相等,由E为BC的中点,得到两条线段相等,再由对应角相等,利用ASA可得出三角形ABE与三角形FCE全等;2由△ABE≌△FCE,根据全等三角形的对应边相等得到AB=CF；再由AB与CF平行,根据一组对边平行且相等的四边形为平行四边形得到ABFC为平行四边形,根据平行四边形的对角线互相平分得到AE=EF,BE=EC；再由∠AEC为三角形ABE的外角,利用外角的性质得到∠AEB等于∠ABE+∠EAB,再由∠AEC=2∠ABC,得到∠ABE=∠EAB,利用等角对等边可得出AE=BE,可得出AF=BC,利用对角线相等的平行四边形为矩形可得出ABFC为矩形;22. 2012山东济南7分1如图1,在ABCD中,点E,F分别在AB,CD上,AE=CF．求证：DE=BF．2如图2,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数．答案1证明：∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,在△ADE和△CBF中,AD=CB ,∠A=∠C ,AE=CF,∴△ADE≌△CBFSAS;∴DE=BF；2解：∵AB=AC,∠A=40°,∴∠ABC=∠C=12180°－40°=70°,又∵BD是∠ABC的平分线,∴∠DBC=12∠ABC=35°;∴∠BDC=180°－∠DBC－∠C=75°;考点平行四边形的性质,全等三角形的判定和性质；等腰三角形的性质,角平分线的定义,角形的内角和定理;分析1根据四边形ABCD是平行四边形,利用平行四边形的性质得到一对边和一对角的对应相等,在加上已知的一对边的相等,由“SAS”,证得△ADE≌△CBF,最后根据全等三角形的对应边相等即可得证;2根据AB=AC,利用等角对等边和已知的∠A的度数求出∠ABC和∠C的度数,再根据已知的BD是∠ABC的平分线,利用角平分线的定义求出∠DBC的度数,最后根据三角形的内角和定理即可求出∠BDC的度数;23. 2012山东潍坊10分如图,已知平行四边形ABCD,过A作AM⊥BC于M,交BD于E,过C作CN⊥AD于N,交BD于F,连结AF、CE．。

2012年全国中考数学试题分类解析汇编(159套63专题）专题44：矩形、菱形、正方形一、选择题1. （2012天津市3分）如图，在边长为2的正方形ABCD中，M为边AD的中点，延长MD 至点E，使ME=MC，以DE为边作正方形DEFG，点G在边CD上，则DG的长为【】（A1（B）3（C（D1【答案】D。

【考点】正方形的性质，勾股定理。

【分析】利用勾股定理求出CM的长，即ME的长，有DM=DE，所以可以求出DE，从而得到DG的长：∵四边形ABCD是正方形，M为边AD的中点，∴DM=12DC=1。

∴CM=1。

∵四边形EDGF1。

故选D。

2. （2012安徽省4分）为增加绿化面积，某小区将原来正方形地砖更换为如图所示的正八边形植草砖，更换后，图中阴影部分为植草区域，设正八边形与其内部小正方形的边长都为a，则阴影部分的面积为【】A.22a B. 32a C. 42a D.52a【答案】A。

【考点】正多边形和圆，等腰直角三角形的性质，正方形的性质。

【分析】图案中间的阴影部分是正方形，面积是2a ，由于原来地砖更换成正八边形，四周一个阴影部分是对角线为a 的正方形的一半，它的面积用对角线积的一半来计算：222114222a a a +⨯⨯=。

故选A 。

3. （2012山西省2分）如图，已知菱形ABCD 的对角线AC ．BD 的长分别为6cm 、8cm ，AE⊥BC 于点E ，则AE 的长是【 】A ．B ．C ．48cm 5D ．24cm 5 【答案】D 。

【考点】菱形的性质，勾股定理。

【分析】∵四边形ABCD 是菱形，∴CO=12AC=3，BO=12BD=，AO⊥BO，∴5=。

∴ABCD 11S BD AC 682422=⋅=⨯⨯=菱形。

又∵ABCD S BC AE =⋅菱形，∴BC·AE=24，即()24AE cm 5=。

故选D 。

4. （2012陕西省3分）如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，OE⊥AB，垂足为E ，若∠ADC=1300，则∠AOE 的大小为【 】A ．75°B ．65°C ．55°D ．50°【答案】B 。

2012年全国中考数学试题分类解析汇编（159套63专题）专题3_整式2（教师篇）2012年全国中考数学试题分类解析汇编(159套63专题）专题3：整式⼀、选择题1. （2012上海市4分）在下列代数式中，次数为3的单项式是【】A ． xy 2B ．x 3+y 3C ．．x 3yD ．3xy 【答案】A 。

2. （2012重庆市4分）计算)2ab 的结果是【】 A ．2ab B ．2a b C ．22a b D ．2ab 【答案】C 。

3. （2012安徽省4分）计算32)2(x -的结果是【】A.52x -B. 68x -C.62x -D.58x -【答案】B 。

4. （2012安徽省4分）某企业今年3⽉份产值为a 万元，4⽉份⽐3⽉份减少了10％，5⽉份⽐4⽉份增加了15％，则5⽉份的产值是【】A.（a －10％）（a +15％）万元B. a （1－10％）（1+15％）万元C.（a －10％+15％）万元D. a （1－10％+15％）万元【答案】B 。

5. （2012⼭西省2分）下列运算正确的是【】A ．B ．C ．a 2a 4=a 8D ．（﹣a 3）2=a 6【答案】D 。

6. （2012海南省3分）计算23x x ?，正确结果是【】A ．6xB ．5xC ．9xD ．8x 【答案】B 。

7. （2012海南省3分）当x 2=-时，代数式x +3的值是【】A ．1B ．－1C ．5D ．－5【答案】A 。

8. （2012陕西省3分）计算32(5a )-的结果是【】A ．510a -B ．610aC ．525a -D ．625a 【答案】D 。

9. （2012宁夏区3分）下列运算正确的是【】A ．223a a =3-B ．235(a )=aC ．369a a =a ?D ．222(2a )=4a 【答案】C 。

10. （2012⼴东佛⼭3分）23a a ?等于【】A ．5aB ．6aC ．8aD ．9a 【答案】A 。

2012年全国各地中考数学试题分类解析汇编第一章有理数（1）1、（2012•遵义）-（-2）的值是（）A．-2 B．2 C．±2 D．4考点：相反数．专题：存在型．分析：根据相反数的定义可知，-（-2）是-2的相反数，由于-2＜0，所以-（-2）=2．解答：∵-（-2）是-2的相反数，-2＜0，∴-（-2）=2．故选B．点评：本题考查的是相反数的定义，即只有符号不同的两个数叫做互为相反数．2、（2012•遵义）据有关资料显示，2011年遵义市全年财政总收入202亿元，将202亿用科学记数法可表示（）A．2.02×102 B．202×108 C．2.02×109 D．2.02×1010考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：将202亿用科学记数法表示为：202亿元=20200000000元=2.02×1010元，故选D．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．3、（2012•自贡）|-3|的倒数是（）A．-3 B．-1/3 C．3 D．1 /3考点：倒数；绝对值．分析：先计算|-3|=3，再求3的倒数，即可得出答案．解答：∵|-3|=3，∴|-3|的倒数是1 /3 ．故选：D．点评：本题考查了倒数、绝对值的概念，熟练掌握绝对值与倒数的意义是解题关键．4、（2012•自贡）自贡市约330万人口，用科学记数法表示这个数为（）A．330×104 B．33×105 C．3.3×105 D．3.3×106考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：将330万=3300000用科学记数法表示为：3.3×106．故选：D．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．5、（2012•重庆）在-3，-1，0，2这四个数中，最小的数是（）A．-3 B．-1 C．0 D．2考点：有理数大小比较．分析：画出数轴，在数轴上标出各点，再根据数轴的特点进行解答即可．解答：这四个数在数轴上的位置如图所示：由数轴的特点可知，这四个数中最小的数是-3．故选A．点评：本题考查的是有理数的大小比较，利用数形结合比较出有理数的大小是解答此题的关键•．6、（2012•肇庆）计算-3+2的结果是（）A．1 B．-1 C．5 D．-5考点：有理数的加法．专题：计算题．分析：根据有理数的加法运算法则计算即可得解．解答： -3+2，=-（3-2），=-1．故选B．点评：本题考查了有理数的加法运算，是基础题，熟记运算法则是解题的关键．7、（2012•肇庆）用科学记数法表示5700000，正确的是（）A．5.7×106 B．57×105 C．570×104 D．0.57×107考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于5700000有7位，所以可以确定n=7-1=6．解答： 5 700 000=5.7×106．故选A．点评：此题考查科学记数法表示较大的数的方法，准确确定n值是关键．8、（2012•张家界）-2012的相反数是（）A．-2012 B．2012 C．-1/2012 D．1 /2012考点：相反数．分析：据相反数的性质，互为相反数的两个数和为0，采用逐一检验法求解即可．解答：根据概念，（-2012的相反数）+（-2012）=0，则-2012的相反数是2012．故选B．点评：本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“-”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．9、（2012•湛江）2的倒数是（）A．2 B．-2 C．1/2 D．-1 /2考点：倒数．分析：直接根据倒数的定义进行解答即可．解答：∵2×1 /2 =1，∴2的倒数是1 /2 ．故选C．点评：本题考查的是倒数的定义，即乘积是1的两数互为倒数．10、（2012•湛江）国家发改委已于2012年5月24日核准广东湛江钢铁基地项目，项目由宝钢湛江钢铁有限公司投资建设，预计投产后年产10200000吨钢铁，数据10200000用科学记数法表示为（）A．102×105 B．10.2×106 C．1.02×106 D．1.02×107考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：将10200000用科学记数法表示为：1.02×107．故选：D．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．11、（2012•玉林）计算：22 =（）A．1 B．2 C．4 D．8考点：有理数的乘方．分析：利用有理数乘方的意义求得结果即可．解答：原式=2×2=4，故选C．点评：本题考查了有理数的乘方，属于基本运算，比较简单．12、（2012•益阳）-2的绝对值等于（）A．2 B．-2 C．1/2 D．±2考点：绝对值．专题：计算题．分析：根据绝对值的性质，当a是正有理数时，a的绝对值是它本身a；即可解答．解答：根据绝对值的性质，|2|=2．故选A．点评：本题考查了绝对值的性质，①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数-a；③当a是零时，a的绝对值是零．13、（2012•义乌市）-2的相反数是（）A．2 B．-2 C．±2 D．-1/2考点：相反数．分析：根据相反数的定义进行解答即可．解答：由相反数的定义可知，-2的相反数是-（-2）=2．故选A．点评：本题考查的是相反数的定义，即只有符号不同的两个数叫做互为相反数．14、（2012•宜昌）如图，数轴上表示数-2的相反数的点是（）A．点P B．点Q C．点M D．点N考点：数轴；相反数．分析：根据数轴得出N、M、Q、P表示的数，求出-2的相反数，根据以上结论即可得出答案．解答：从数轴可以看出N表示的数是-2，M表示的数是-0.5，Q表示的数是0.5，P表示的数是2，∵-2的相反数是2，∴数轴上表示数-2的相反数是点P，故选A．点评：本题考查了数轴和相反数的应用，主要培养学生的观察图形的能力和理解能力，题型较好，难度不大．15、（2012•宜昌）2012年4月30日，我国在西昌卫星发射中心用“长征三号乙”运载火箭成功发射两颗北斗导航卫星，其中静止轨道卫星的高度约为36000km．这个数据用科学记数法表示为（）A．36×103km B．3.6×103km C．3.6×104km D．0.36×105km考点：科学记数法—表示较大的数．分析：科学记数法就是将一个数字表示成（a×10的n次幂的形式），其中1≤|a|＜10，n表示整数．n为整数位数减1，即从左边第一位开始，在首位非零的后面加上小数点，再乘以10的n次幂．解答：36000=3.6×104km．故选C．点评：用科学记数法表示一个数的方法是（1）确定a：a是只有一位整数的数；（2）确定n：当原数的绝对值≥10时，n为正整数，n等于原数的整数位数减1；当原数的绝对值＜1时，n为负整数，n的绝对值等于原数中左起第一个非零数前零的个数（含整数位数上的零）．16、（2012•宜宾）-3的倒数是（）A．1/3 B．3 C．-3 D．-1 /3考点：倒数．分析：据倒数的定义，互为倒数的两数乘积为1，-3×（-1 /3）=1．解答：根据倒数的定义得：-3×（-1 /3 ）=1，因此倒数是-1/ 3 ．故选：D．点评：此题考查的是倒数，关键明确倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．需要注意的是负数的倒数还是负数．17、（2012•扬州）-3的绝对值是（）A．3 B．-3 C．-3 D．1/3考点：绝对值．分析：计算绝对值要根据绝对值的定义求解．第一步列出绝对值的表达式；第二步根据绝对值定义去掉这个绝对值的符号．解答：-3的绝对值是3．故选：A．点评：此题主要考查了绝对值的定义，规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．18、（2012•扬州）今年我市参加中考的人数大约有41300人，将41300用科学记数法表示为（）A．413×102 B．41.3×103 C．4.13×104 D．0.413×103考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答： 41300=4.13×104，故选：C．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．19、（2012•孝感）我国平均每平方千米的土地上，一年从太阳得到的能量相当于燃烧130000吨煤所产生的能量．130000用科学记数法表示为（）A．13×104 B．1.3×105 C．0.13×106 D．1.3×108考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：130000=1.3×105，故选：B．点评：此题主要考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．20、（2012•襄阳）一个数的绝对值等于3，这个数是（）A．3 B．-3 C．±3 D．1/3考点：绝对值．分析：根据绝对值的定义即可求解．解答：因为|3|=3，|-3|=3，所以绝对值等于3的数是±3．故选C．点评：规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．本题是绝对值性质的逆向运用，此类题要注意答案一般有2个，除非绝对值为0的数才只有一个为0．21、（2012•襄阳）李阳同学在“百度”搜索引擎中输入“魅力襄阳”，能搜索到与之相关的结果个数约为236 000，这个数用科学记数法表示为（）A．2.36×103 B．236×103 C．2.36×105 D．2.36×106考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：236 000=2.36×105，故选：C．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．22、（2012•咸宁）-8的相反数是（）A．-8 B．8 C．-1/8 D．1/8考点：相反数．分析：直接根据相反数的定义进行解答即可．解答：由相反数的定义可知，-8的相反数是-（-8）=8．故选B．点评：本题考查的是相反数的定义，即只有符号不同的两个数叫做互为相反数．23、（2012•咸宁）南海是我国固有领海，它的面积超过东海、黄海、渤海面积的总和，约为360万平方千米，360万用科学记数法表示为（）A．3.6×102 B．360×104 C．3.6×104 D．3.6×106考点：科学记数法—表示较大的数．分析：单位为“万”，换成计数单位为1的数，相当于把原数扩大10000倍，进而把得到的数表示成a×10n的形式，a为3.6，n为整数数位减去1．解答：360万=3600000=3.6×106，故选D．点评：考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．24、（2012•武汉）在2.5，-2.5，0，3这四个数种，最小的数是（）A．2.5 B．-2.5 C．0 D．3考点：有理数大小比较．分析：根据有理数的大小比较法则是负数都小于0，正数都大于0，正数大于一切负数进行比较即可．解答：∵-2.5＜0＜2.5＜3，∴最小的数是-2.5，故选B．点评：本题考查了有理数的大小比较法则的应用，有理数的大小比较法则是：负数都小于0，正数都大于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．25、（2012•武汉）某市2012年在校初中生的人数约为23万．数230000用科学记数法表示为（）A．23×104 B．2.3×105 C．0.23×103 D．0.023×106考点：科学记数法—表示较大的数．专题：常规题型．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于23万有6位，所以可以确定n=6-1=5．解答：23万=230 000=2.3×105．故选B．点评：此题考查科学记数法表示较大的数的方法，准确确定n值是关键．26、（2012•潍坊）许多人由于粗心，经常造成水龙头“滴水”或“流水”不断．根据测定，一般情况下一个水龙头“滴水”1个小时可以流掉3.5千克水，若1年按365天计算，这个水龙头1年可以流掉（）千克水．（用科学记数法表示，保留3个有效数字）A．3.1×104 B．0.31×105 C．3.06×104 D．3.07×104考点：科学记数法与有效数字．分析：先列式表示1年水龙头滴水的重量，再把结果用科学记数法表示．有效数字是从左边第一个不是0的数字起，后面所有的数字都是有效数字．用科学记数法表示的数的有效数字只与前面的a有关，与10的多少次方无关．解答：3.5×24×365=30660=3.066×104≈3.07×104故选D．点评：此题主要考查了有理数的乘法在实际生活中的应用，科学记数法的表示方法，以及用科学记数法表示的数的有效数字的确定方法．27、（2012•铜仁地区）从权威部门获悉，中国海洋面积是299.7万平方公里，约为陆地面积的三分之一，299.7万平方公里用科学记数法表示为（）平方公里（保留两位有效数字）A．3×106 B．0.3×107 C．3.0×106 D．2.99×106考点：科学记数法与有效数字．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于299.7万有7位，所以可以确定n=7-1=6．有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字．用科学记数法表示的数的有效数字只与前面的a有关，与10的多少次方无关．解答：299.7万=2.997×106≈3.0×106．故选：C．点评：此题主要考查了科学记数法的表示方法，以及用科学记数法表示的数的有效数字的确定方法．28、（2012•天门）2012的绝对值是（）A．2012 B．-2012 C．1/2012 D．-1/2012考点：绝对值．专题：计算题．分析：根据绝对值的性质直接解答即可．解答：∵2012是正数，∴|2012|=2012，故选A．点评：本题考查了绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．29、（2012•天门）吸烟有害健康．据中央电视台2012年5月30日报道，全世界每因吸烟引起的疾病致死的人数大约为600万，数据600万用科学记数法表示为（）A．0.6×107 B．6×106 C．60×105 D．6×105考点：科学记数法—表示较大的数．分析：首先把600万化为6000000，再用科学记数法表示，科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：600万=6000000=6×106，故选：B．点评：此题主要考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．30、（2012•天津）据某域名统计机构公布的数据显示，截至2012年5月21日，我国“．NET”域名注册量约为560000个，居全球第三位，将560000用科学记数法表示应为（）A．560×103 B．56×104 C．5.6×105 D．0.56×106考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于560000有6位，所以可以确定n=6-1=5．解答：560 000=5.6×105．故选C．点评：此题考查科学记数法表示较大的数的方法，准确确定n值是关键．31、（2012•泰州）过度包装既浪费资源又污染环境．据测算，如果全国每年减少10%的过度包装纸用量，那么可减排二氧化碳3120000吨，把数3120000用科学记数法表示为（）A．3.12×105 B．3.12×106 C．31.2×105 D．0.312×107考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：将3120000用科学记数法表示为：3.12×106．故选：B．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．32、（2012•泰安）下列各数比-3小的数是（）A．0 B．1 C．-4 D．-1考点：有理数大小比较．分析：首先判断出1＞-3，0＞-3，求出每个数的绝对值，根据两负数比较大小，其绝对值大的反而小，求出即可．解答：根据两负数比较大小，其绝对值大的反而小，正数都大于负数，零大于一切负数，∴1＞-3，0＞-3，∵|-3|=3，|-1|=1，|-4|=4，∴比-3小的数是负数，是-4．故选C ．点评：本题考查了有理数的大小比较法则和绝对值等知识点的应用，注意：正数都大于负数，两负数比较大小，其绝对值大的反而小，题型较好，但是一道比较容易出错的题目．33、（2012•泰安）已知一粒米的质量是0.000021千克，这个数字用科学记数法表示为（ ）A ．21×104-千克B ．2.1×106-千克C ．2.1×105-千克D ．21×104-千克考点：科学记数法—表示较小的数．分析：绝对值小于1的正数也可以利用科学记数法表示，一般形式为a ×10n -，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．解答： 0.000021=2.1×105-； 故选：C ．点评：本题考查了用科学记数法表示较小的数，一般形式为a ×10n -，其中1≤|a|＜10，n 为由原数左边起第一个不为零的数字前面的0的个数所决定．34、（2012•台州）计算-1+1的结果是（ ）A ．1B ．0C ．-1D ．-2考点：有理数的加法．专题：常规题型．分析：根据互为相反数的和等于0解答．解答： -1+1=0．故选B ．点评：本题考查了有理数的加法运算，是基础题，熟记运算法则是解题的关键．35、（2012•台湾）计算（-100051）×（5-10）之值为何？（ ）A ．1000B ．1001C ．4999D ．5001考点：有理数的乘法．专题：计算题．分析：将-100051化为-（1000+51），然后计算出5-10，再根据分配律进行计算． 解答：原式=-（1000+51）×（-5）=（1000+51）×5 =1000×5+51×5=5000+1=5001．故选D．点评：本题考查了有理数的乘法，灵活运用分配律是解题的关键．36、（2012•台湾）如图是利用短除法求出三数8、12、18的最大公因子的过程．利用短除法，求出这三数的最小公倍数为何？（）A．12 B．72 C．216 D．432考点：有理数的除法．专题：常规题型．分析：继续完善短除法，然后根据最小公倍数的求法，把所有的数相乘即可．解答：如图，完成短除法如下最小公倍数为2×2×3×2×1×3=72．故选B．点评：本题考查了短除法求最小公倍数的方法，属于小学内容，比较简单，完善短除过程是解题的关键．37、（2012•台湾）已知某公司去年的营业额为四千零七十亿元，则此营业额可用下列何者表示？（）A．4.07×109元 B．4.07×1010元 C．4.07×1011元 D．4.07×1012元考点：科学记数法—表示较大的数．分析：首先将四千零七十亿元可写成407000000000，再利用科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：将四千零七十亿元可写成407000000000，407000000000=4.07×1011，故选：C．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．38、（2012•随州）湿地旅游爱好者小明了解到鄂东南某市水资源总量为42.43亿立方米，其中42.43亿用科学记数法可表示为（）A．42.43×109 B．4.423×108 C．4.243×109 D．0.423×108考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：根据42.43亿=4243000000，用科学记数法表示为：4.243×109．故选：C．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．39、（2012•宿迁）-8的绝对值是（）A．8 B．1/8 C．-1/8 D．-8考点：绝对值．分析：根据负数的绝对值等于它的相反数解答．解答： -8的绝对值为|-8|=8．故选A．点评：本题考查了绝对值的性质，熟记一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0是解题的关键．40、（2012•沈阳）沈阳地铁2号线的开通，方便了市民的出行．从2012年1月9日到2月7日的30天里，累计客运量约达3040000人次，将3040000用科学记数法表示为（）A．3.04×105 B．3.04×106 C．30.4×105 D．0.304×107考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：将3040000用科学记数法表示为3.04×106．故选B．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．41、（2012•深圳）第八届中国（深圳）文博会以总成交额143 300 000 000元再创新高，将数143 300 000 000用科学记数法表示为（）A．1.433×1010 B．1.433×1011 C．1.433×1012 D．0.1433×1012考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于143 300 000 000有12位，所以可以确定n=12-1=11．解答：143 300 000 000=1.433×1011．故选B．点评：此题考查科学记数法表示较大的数的方法，准确确定n值是关键．42、（2012•绍兴）3的相反数是（）A．3 B．-3 C．1/3 D．-1/3考点：相反数．分析：根据相反数的意义，3的相反数即是在3的前面加负号．解答：根据相反数的概念及意义可知：3的相反数是-3．故选B．点评：本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“-”号；一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．43、（2012•绍兴）据科学家估计，地球年龄大约是4 600 000 000年，这个数用科学记数法表示为（）A．4.6×108 B．46×108 C．4.6×109 D．0.46×1010考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答： 4 600 000 000用科学记数法表示为：4.6×109．故选：C．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．44、（2012•陕西）如果零上5℃记作+5℃，那么零下7℃可记作（）A．-7℃ B．+7℃ C．+12℃ D．-12℃考点：正数和负数．分析：在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．解答：∵“正”和“负”相对，∴零上5℃记作+5℃，则零下7℃可记作-7℃．故选A．点评：此题考查了正数与负数的定义．解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．45、（2012•山西）为了实现街巷硬化工程高质量“全覆盖”，我省今年1-4月公路建设累计投资92.7亿元，该数据用科学记数法可表示为（）A．0.927×1010 B．92.7×109 C．9.27×1011 D．9.27×109考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：将92.7亿=9270000000用科学记数法表示为：9.27×109．故选：D．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．46、（2012•日照）-5的相反数是（）A．-5 B．-1/5 C．5 D．1/5考点：相反数．分析：根据相反数的定义解答．解答：只有符号不同的两个数称为互为相反数，则-5的相反数为5，故选C．点评：本题考查了相反数的定义，只有符号不同的两个数互为相反数，a的相反数是-a．47、（2012•日照）据新华社报道：在我国南海某海域探明可燃冰储量约有194亿立方米．194亿用科学记数法表示为（）A．1.94×1010 B．0.194×1010 C．19.4×109 D．1.94×109考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：194亿=19400000000，用科学记数法表示为：1.94×1010．故选：A．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．48、（2012•泉州）-7的相反数是（）A．-7 B．7 C．-1/7 D．1/7考点：相反数．分析：据相反数的性质，互为相反数的两个数和为0，采用逐一检验法求解即可．解答：根据概念，（-7的相反数）+（-7）=0，则-7的相反数是7．故选B．点评：本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“-”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．49、（2012•衢州）下列四个数中，最小的数是（ ） A ．2 B ．-2 C ．0 D ．-1/2 考点：有理数大小比较． 专题：探究型．分析：根据有理数比较大小的法则进行比较即可． 解答：∵2＞0，-2＜0，-1/2 ＜0， ∴可排除A 、C ，∵|-2|=2，|-1 /2 |=1 2 ，2＞1/ 2 ， ∴-2＜-1/ 2 ． 故选B ．点评：本题考查的是有理数的大小比较，熟知正数都大于0； 负数都小于0； 正数大于一切负数； 两个负数，绝对值大的其值反而小是解答此题的关键．50、（2012•衢州）衢州市是国家优秀旅游城市，吸引了众多的海内外游客．据衢州市2011年国民经济和社会发展统计报显示，全年旅游总收入达121.04亿元．将121.04亿元用科学记数法可表示为（ ）A ．12.104×109元B ．12.104×1010元C ．1.2104×1010元D ．1.2104××1011元 考点：科学记数法—表示较大的数． 分析：科学记数法的表示形式为a ×10n的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n 是正数；当原数的绝对值＜1时，n 是负数．解答：将121.04亿用科学记数法表示为：121.04亿元=12104000000元=1.2104×1010元， 故选；C ．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a ×10n的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值． 51、（2012•青岛）-2的绝对值是（ ）A ．-1/2B ．-2C ．1 /2D ．2 考点：绝对值．分析：根据绝对值的定义：数轴上某个数与原点的距离叫做这个数的绝对值．则-2的绝对值就是表示-2的点与原点的距离．解答： |-2|=2， 故选：D ．点评：此题主要考查了绝对值，关键是掌握：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．52、（2012•黔西南州）-141的倒数是（ ） A ．-45 B ．45 C ．-54 D ．54考点：倒数．。

2012年全国中考数学试题分类解析汇编(159套63专题）专题24：方程、不等式和函数的综合一、选择题1. （2012福建龙岩4分）下列函数中，当x ＜0时，函数值y 随x 的增大而增大的有【 】 ①y=x ②y=－2x ＋1 ③1y=x -④2y=3x A ．1个B ．2个C ．3个D ． 4个 【答案】B 。

【考点】一次函数、反比例函数和二次函数的性质。

【分析】根据一次函数、反比例函数和二次函数的性质作出判断：①∵y=x 的k ＞0，∴当x ＜0时，函数值y 随x 的增大而增大；②∵y=－2x ＋1的k ＜0，∴当x ＜0时，函数值y 随x 的增大而减小；③∵1y=x-的k ＜0，∴当x ＜0时，函数值y 随x 的增大而增大； ④∵2y=3x 的a ＞0，对称轴为x=0，∴当x ＜0时，函数值y 随x 的增大而减小。

∴正确的有2个。

故选B 。

2. （2012四川广元3分） 已知关于x 的方程22(x 1)(x b)2++-=有唯一实数解，且反比例函数1b y x+=的图象在每个象限内y 随x 的增大而增大，那么反比例函数的关系式为【 】 A. 3y x =- B. 1y x = C. 2y x = D. 2y x=- 【答案】D 。

【考点】一元二次方程根的判别式，反比例函数的性质。

【分析】关于x 的方程22(x 1)(x b)2++-=化成一般形式是：2x 2＋（2－2b ）x ＋（b 2－1）=0，∵它有唯一实数解，∴△=（2－2b ）2－8（b 2－1）=－4（b ＋3）（b －1）=0，解得：b=－3或1。

∵反比例函数1b y x+= 的图象在每个象限内y 随x 的增大而增大， ∴1+b＜0。

∴b＜－1。

∴b=－3。

∴反比例函数的解析式是13y x -=，即2y x=-。

故选D 。

3. （2012山东菏泽3分）已知二次函数2y ax bx c =++的图象如图所示，那么一次函数y bx c =+和反比例函数a y x=在同一平面直角坐标系中的图象大致是【 】 A ．B ．C ． D【答案】C 。

2012年全国中考数学试题分类解析汇编(159套63专题）专题29：投影与视图一、选择题1. （2012北京市4分）下图是某个几何体的三视图，该几何体是【】A．长方体 B．正方体 C．圆柱 D．三棱柱【答案】D。

【考点】由三视图判断几何体。

【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，由于主视图和左视图为矩形，可得为柱体，俯视图为三角形可得为三棱柱。

故选D。

2. （2012天津市3分）右图是一个由4个相同的正方体组成的立体图形，它的三视图是【】【答案】A。

【考点】简单组合体的三视图。

【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形。

从正面看可得从左往右2列正方形的个数依次为1，2；从左面看可得到从左往右2列正方形的个数依次为2，1；从上面看可得从上到下2行正方形的个数依次为1，2。

故选A。

3. （2012安徽省4分）下面的几何体中，主（正）视图为三角形的是【】A. B.C. D.【答案】C。

【考点】判断立体图形的三视图。

【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形。

因此，根据这几个常见几何题的视图可知：圆柱的主视图是矩形，正方体的主视图是正方形，圆锥的主视图是三角形，三棱柱的主视图是宽相等两个相连的矩形。

故选C。

4. （2012山西省2分）如图所示的工件的主视图是【】A．B．C．D．【答案】B。

【考点】简单组合体的三视图。

【分析】从物体正面看，看到的是一个横放的矩形，且一条斜线将其分成一个直角梯形和一个直角三角形。

故选B。

5. （2012海南省3分）如图竖直放置的圆柱体的俯视图是【】A．长方体 B．正方体 C．圆 D．等腰梯形【答案】C。

【考点】简单组合体的三视图。

【分析】找到从上面看所得到的图形即可：从上面看易得是圆。

故选C。

6. （2012陕西省3分）如图，是由三个相同的小正方体组成的几何体，该几何体的左视图是【】A．B．C．D．【答案】C。

2012年全国中考数学试题分类解析汇编(159套63专题）专题31：折叠问题一、选择题1. （2012广东梅州3分）如图，在折纸活动中，小明制作了一张△ABC 纸片，点D 、E 分别是边AB 、AC 上，将△ABC 沿着DE 折叠压平，A 与A′重合，若∠A=75°，则∠1+∠2=【 】A ．150°B ．210°C ．105°D ．75°【答案】A 。

【考点】翻折变换（折叠问题），三角形内角和定理。

【分析】∵△A′DE 是△ABC 翻折变换而成，∴∠AED=∠A′ED，∠ADE=∠A′DE，∠A=∠A′=75°。

∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣75°=105°，∴∠1+∠2=360°﹣2×105°=150°。

故选A 。

2. （2012江苏南京2分）如图，菱形纸片ABCD 中，∠A=600，将纸片折叠，点A 、D 分别落在A’、D’处，且A’D’经过B ，EF 为折痕，当D’F ⊥CD 时，CF FD的值为【 】A. 12-B. 6C. 16D. 18【答案】A 。

【考点】翻折变换（折叠问题），菱形的性质，平行的性质，折叠的性质，锐角三角函数定义，特殊角的三角函数值。

【分析】延长DC 与A′D′，交于点M ，∵在菱形纸片ABCD 中，∠A=60°，∴∠DCB=∠A=60°，AB∥CD。

∴∠D=180°-∠A=120°。

根据折叠的性质，可得∠A′D′F=∠D=120°，∴∠FD′M=180°-∠A′D′F=60°。

∵D′F⊥CD，∴∠D′FM=90°，∠M=90°-∠FD′M=30°。

∵∠BCM=180°-∠BCD=120°，∴∠CBM=180°-∠BCM -∠M=30°。

2012年全国中考数学试题分类解析汇编(159套63专题）专题33：网格问题一、选择题1. （2012宁夏区3分）一个几何体的三视图如图所示，网格中小正方形的边长均为1，那么下列选项中最接近这个几何体的侧面积的是【】A．24.0 B．62.8 C．74.2 D．113.02. （2012湖北孝感3分）如图，△ABC在平面直角坐标系中的第二象限内，顶点A的坐标是(－2，3)，先把△ABC向右平移4个单位长度得到△A1B1C1，再作△A1B1C1关于x轴的对称图形△A2B2C2，则顶点A2的坐标是【】A．(－3，2) B．(2，－3) C．(1，－2) D．(3，－1)3. （2012湖北荆门3分）下列4×4的正方形网格中，小正方形的边长均为1，三角形的顶点都在格点上，则与△ABC相似的三角形所在的网格图形是【】A． B． C． D．4. （2012山东聊城3分）如图，在方格纸中，△ABC经过变换得到△D EF，正确的变换是【】A．把△ABC绕点C逆时针方向旋转90°，再向下平移2格B．把△ABC绕点C顺时针方向旋转90°，再向下平移5格C．把△ABC向下平移4格，再绕点C逆时针方向旋转180°D．把△ABC向下平移5格，再绕点C顺时针方向旋转180°二、填空题1. （2012天津市3分）“三等分任意角”是数学史上一个著名问题．已知一个角∠MAN设1M AN3α∠=∠（Ⅰ）当∠MAN=690时，α∠的大小为▲ （度）；（Ⅱ）如图，将∠MAN放置在每个小正方形的边长为1cm的网格中，角的一边AM与水平方向的网格线平行，另一边AN经过格点B，且AB=2.5cm．现要求只能使用带刻度的直尺，请你在图中作出α∠，并简要说明作法（不要求证明）▲ ．2. （2012浙江杭州4分）如图，平面直角坐标系中有四个点，它们的横纵坐标均为整数．若在此平面直角坐标系内移动点A，使得这四个点构成的四边形是轴对称图形，并且点A的横坐标仍是整数，则移动后点A的坐标为▲ ．3. （2012江苏泰州3分）如图，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点P，则tan∠APD的值是▲ ．三、解答题1. （2012安徽省8分）如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）和点A1.（1）画出一个格点△A1B1C1，并使它与△ABC全等且A与A1是对应点；（2）画出点B关于直线AC的对称点D，并指出AD可以看作由AB绕A点经过怎样的旋转而得到的.2. （2012海南省8分）如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（－2，4）、（－2，0）、（－4，1），结合所给的平面直角坐标系解答下列问题：（1）画出△ABC关于原点O对称的△A1B1C1.（2）平移△ABC，使点A移动到点A2（0，2），画出平移后的△A2B2C2并写出点B2、C2的坐标.（3）在△ABC、△A1B1C1、△A2B2C2中，△A2B2C2与成中心对称，其对称中心的坐标为 .3. （2012广东梅州7分）如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A1OB1．（直接填写答案）（1）点A关于点O中心对称的点的坐标为；（2）点A1的坐标为；（3）在旋转过程中，点B经过的路径为弧BB1，那么弧BB1的长为．4. （2012广东广州12分）如图，⊙P的圆心为P（﹣3，2），半径为3，直线MN过点M（5，0）且平行于y轴，点N在点M的上方．（1）在图中作出⊙P关于y轴对称的⊙P′．根据作图直接写出⊙P′与直线MN的位置关系．（2）若点N在（1）中的⊙P′上，求PN的长．5. （2012浙江温州8分）如图，在方格纸中，△PQR的三个顶点及A,B,C,D,E五个点都在小方格的顶点上，现以A,B,C,D,E中的三个顶点为顶点画三角形，（1）在图甲中画出一个三角形与△PQR全等；（2）在图乙中画出一个三角形与△PQR面积相等但不全等．．．.6. （2012江苏泰州10分）如图，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上，将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1，然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2．（1）在网格中画出△A1B1C1和△A1B2C2；（2）计算线段AC在变换到A1C2的过程中扫过区域的面积（重叠部分不重复计算）7. （2012江苏常州6分）在平面直角坐标系xOy中，已知△ABC和△DEF的顶点坐标分别为A（1，0）、B （3，0）、C（2，1）、D（4，3）、E（6，5）、F（4，7）。

2012年全国中考数学试题分类解析汇编(159套63专题）专题42：解直角三角形和应用一、选择题1. （2012广东深圳3分）小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上；如图，此时测得地面上的影长为8米，坡面上的影长为4米．已知斜坡的坡角为300，同一时 刻，一根长为l 米、垂直于地面放置的标杆在地面上的影长为2米，则树的高度为【 】A.(6+米B.12米C.(4+米 D ．10米 【答案】A 。

【考点】解直角三角形的应用（坡度坡角问题），锐角三角函数定义，特殊角的三角函数值，相似三角形的判定和性质。

【分析】延长AC 交BF 延长线于E 点，则∠CFE=30°。

作CE⊥BD 于E ，在Rt△CFE 中，∠CFE=30°，CF=4，， 在Rt△CED 中，CE=2，∵同一时刻，一根长为1米、垂直于地面放置的标杆在地面上的影长为2米，∴DE=4。

∵△DCE∽△DAB，且CE ：DE=1：2，∴在Rt△ABD 中，AB=12BD=(12=A 。

2. （2012浙江嘉兴、舟山4分）如图，A 、B 两点在河的两岸，要测量这两点之间的距离，测量者在与A 同侧的河岸边选定一点C ，测出AC=a 米，∠A=90°，∠C=40°，则AB 等于【 】米．A ． asin40°B ． acos40°C ． atan40°D ．a tan40【答案】C 。

【考点】解直角三角形的应用，锐角三角函数定义。

【分析】∵△ABC 中，AC=a 米，∠A=90°，∠C=40°，∴AB=atan40°。

故选C 。

3. （2012福建福州4分）如图，从热气球C 处测得地面A 、B 两点的俯角分别为30°、45°，如果此时热气球C 处的高度CD 为100米，点A 、D 、B 在同一直线上，则AB 两点煌距离是【 】A ．200米B ．2003米C ．2203米D ．100(3＋1)米 【答案】D 。