18.2.2菱形的性质与判定练习题

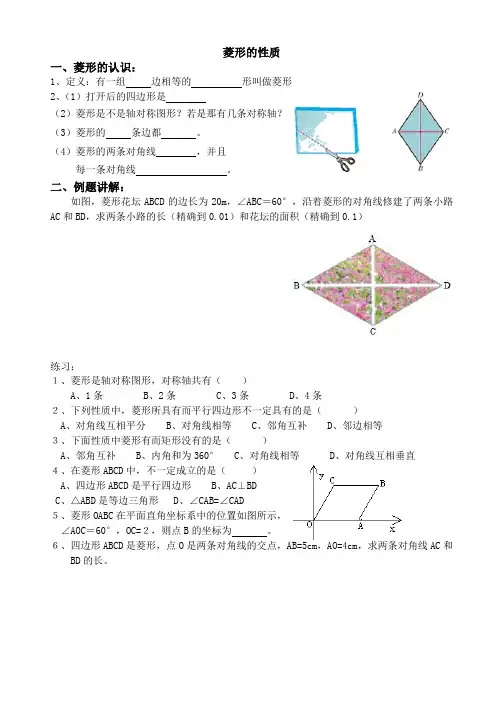
菱形的性质一、菱形的认识：1、定义：有一组边相等的形叫做菱形2、（1）打开后的四边形是（2）菱形是不是轴对称图形？若是那有几条对称轴？（3）菱形的条边都。

（4）菱形的两条对角线，并且每一条对角线。

二、例题讲解：如图，菱形花坛ABCD的边长为20m，∠ABC＝60°，沿着菱形的对角线修建了两条小路AC和BD，求两条小路的长（精确到0.01）和花坛的面积（精确到0.1）练习：１、菱形是轴对称图形，对称轴共有（）A、1条B、2条C、3条D、4条２、下列性质中，菱形所具有而平行四边形不一定具有的是（）A、对角线互相平分B、对角线相等C、邻角互补D、邻边相等３、下面性质中菱形有而矩形没有的是（）A、邻角互补B、内角和为360°C、对角线相等D、对角线互相垂直４、在菱形ABCD中，不一定成立的是（）A、四边形ABCD是平行四边形B、AC⊥BDC、△ABD是等边三角形D、∠CAB=∠CAD５、菱形OABC在平面直角坐标系中的位置如图所示，∠AOC＝60°，OC=２，则点B的坐标为。

６、四边形ABCD是菱形，点O是两条对角线的交点，AB=5cm，AO=4cm，求两条对角线AC和BD的长。

７、如图菱形的两条对角线的长分别是6cm 和8cm ，求菱形的周长和面积。

８、如图，已知菱形ABCD 中，AE ⊥BC 于E 且BE=CE ，AB=2.（1）求证：△ABC 是等边三角形 （2）求对角线BD 的长及菱形ABCD 的面积。

9、如右图，在菱形ABCD 中，E ，F 分别是CB ，CD 上的点，且BE=DF.求证：①△ABE ≌△ADF ；②∠AEF=∠AFE.10、如图，菱形ABCD 中，点E 、F 分别是BC 、CD 上的点，∠B=∠EAF=60°，∠BAE=20°，求∠CEF 的度数。

F ED A B11、如图，在菱形ABCD中，E是AB的中点，且DE⊥AB，AB＝4．求：(1)∠ABC的度数；(2)菱形ABCD的面积．。

人教版八年级数学下册18.2.2.1 菱形的性质同步练习一、选择题（共10小题，3*10=30）1.菱形具有而一般平行四边形不具有的性质是()A．对边相等B．对角相等C．对角线互相平分D．对角线互相垂直2．(2019·贵阳)如图，菱形ABCD的周长是4 cm，∠ABC＝60°，那么这个菱形的对角线AC的长是( ) A．1 cm B．2 cm C．3 cm D．4 cm3. 如图，在△ABC中，AB≠AC，D是BC上一点，DE∥AC交AB于点E，DF∥AB交AC于点F，要使四边形AEDF是菱形，只需添加的条件是()A．AD⊥BC B．∠BAD＝∠CAD C．BD＝DC D．AD＝BD4. 如图，在菱形ABCD中，AB＝4，∠B＝60°，AE⊥BC，AF⊥CD，垂足分别为E，F，连接EF，则△AEF的面积是()A．4 3 B．3 3 C．2 3 D. 35. 如图，菱形ABCD的边AB＝8，∠B＝60°，P是AB上一点，BP＝3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点为A′. 当CA′的长度最小时，CQ的长为()A．5 B．7 C．8 D. 106.如图，在菱形ABCD中，对角线AC，BD相交于点O，BD＝6，AC＝8，直线OE⊥AB交CD于点F，则AE的长为()A．4B．4.8 C．2.4D．3.27. 已知菱形的周长为4 5 ，两条对角线的和为6，则菱形的面积为( )A ．2 B. 5 C ．3 D ．48. 如图，菱形ABCD 的对角线AC ，BD 交于点O ，AC ＝4，BD ＝16，将△ABO 沿点A 到点C 的方向平移，得到△A′B′O′.当点A′与点C 重合时，点A 与点B′之间的距离为( )A ．6B ．8C ．10D ．129. 如图，四边形ABCD 是菱形，AC ＝8，DB ＝6，DH ⊥AB 于H ，则DH 等于( )A ．245B ．125C ．5D ．410．如图，在周长为12的菱形ABCD 中，AE ＝1，AF ＝2，若P 为对角线BD 上一动点，则EP ＋FP 的最小值为( )A ．1B ．2C ．3D ．4二．填空题（共8小题，3*8=24）11. 菱形的两条对角线长分别是5和12，则此菱形的边长是_______，面积是_______．12．在菱形ABCD 中，对角线AC 、BD 相交于点O ，若AB ＝7 cm ，则周长是________cm.13. 如图，在菱形ABCD 中，对角线AC 、BD 相交于点O ，若∠ABC ＝110°，则∠BAD ＝________°， ∠ABD ＝________°，∠BCA ＝________°.14．如图，已知菱形ABCD的对角线AC，BD交于点O，E为BC的中点，若OE＝3，则菱形的周长为_______．15．如图，在菱形ABCD中，对角线AC与BD相交于点O，若AB＝2，∠ABC＝60°，则BD的长为________．16．如图，四边形ABCD是菱形，O是两条对角线的交点，过点O的三条直线将菱形分成阴影和空白部分，当菱形的两条对角线的长分别为6和8时，阴影部分的面积为_______．17. 如图，四边形ABCD为菱形，A，B两点的坐标分别是(2，0)，(0，1)，点C，D在坐标轴上，则菱形ABCD的周长等于________.18. 如图，在菱形ABCD中，E是AC的中点，EF∥CB，交AB于点F，如果EF＝3，那么菱形ABCD 的周长为________.三．解答题（共7小题，46分）19．(6分) 如图，已知菱形的周长为40 cm，两邻角度数之比为1∶2.(1)求菱形的两条对角线的长；(2)求菱形的面积．20．(6分) 如图，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE.求证：OE＝BC.21．(6分) 如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE＝AB，连接CE，若∠E＝50°，求∠BAO的大小．22．(6分) 已知：如图，在菱形ABCD中，点E、F分别为边CD、AD的中点，连接AE，CF，求证：△ADE≌△CDF.23．(6分) 如图，在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED＝∠ABC，∠ABF＝∠BPF.求证：(1)△ABF≌△DAE；(2)DE＝BF＋EF.24．(8分) 如图，菱形ABCD的两条对角线相交于点O，∠DAC＝30°，BD＝12(1)求∠ABC的度数；(2)求菱形ABCD的面积．25．(8分) 在菱形ABCD中，∠B＝60°，点E在边BC上，点F在边CD上．(1)如图①，若E是BC的中点，∠AEF＝60°，求证：BE＝DF；(2)如图②，若∠EAF＝60°，求证：△AEF是等边三角形．参考答案1-5DABBB 6-10 DDCAC11. 6.5，3012. 2813. 70，55，3514. 24 15. 2 316. 1217．4518．2419. 解：(1) ∵四边形ABCD 是菱形，两邻角度数之比为1∶2， ∴∠ABC=∠BAC=60°又∵菱形的周长为40 cm ，AC ＝AB=10 cm ，BD ＝2BO=2×AB 2-AO 2 =2×102-52 =10 3 cm(2)S 菱形＝12BD·AC ＝50 3 cm 2 20. 解：∵DE ∥AC ，CE ∥BD ，∴四边形OCED 是平行四边形， ∵四边形ABCD 是菱形，∴AC ⊥BD ，∴∠DOC ＝90°，∴四边形OCED 是矩形，∴OE ＝CD ，∵四边形ABCD 是菱形，∴CD ＝BC ，∴OE ＝BC21. 解：菱形ABCD 中，AB ＝BC ，∵BE ＝AB ，∴BC ＝BE ，∴∠BCE ＝∠E ＝50°，∴∠CBE ＝180°－50°×2＝80°，∵AD ∥BC ，∴∠BAD ＝∠CBE ＝80°，∴∠BAO ＝12×80°＝40°. 22. 证明：∵四边形ABCD 是菱形，∴AD ＝CD ，∵点E 、F 分别为边CD 、AD 的中点，∴AD ＝2DF ，CD ＝2DE ，∴DE ＝DF ，在△ADE 和△CDF 中，⎩⎪⎨⎪⎧AD ＝CD ，∠ADE ＝∠CDF ，DE ＝DF ，∴△ADE ≌△CDF(SAS)．23. 证明：(1)∵四边形ABCD 是菱形，∴AB ＝AD ，AD ∥BC ， ∴∠BPA ＝∠DAE ，∵∠ABC ＝∠AED ，∴∠BAF ＝∠ADE ，∵∠ABF ＝∠BPF ，∠BPA ＝∠DAE ，∴∠ABF ＝∠DAE ， ∵AB ＝DA ，∴△ABF ≌△DAE(ASA)(2)∵△ABF ≌△DAE ，∴AE ＝BF ，DE ＝AF ，∵AF ＝AE ＋EF ＝BF ＋EF ，∴DE ＝BF ＋EF24. 解：(1)∵菱形ABCD 的两条对角线相交于点O ，∠DAC ＝30°， ∴∠BAD ＝2∠DAC ＝60°，∵AD ∥BC ，∴∠ABC ＝180°－60°＝120°；(2)∵菱形ABCD 的两条对角线相交于点O ，BD ＝12，∴AC ⊥BD ，DO ＝12BD ＝6， 又∵∠DAC ＝30°，∴AD ＝2DO ＝12，∴Rt △AOD 中，AO ＝122－62＝63，∴AC ＝2AO ＝123，∴菱形ABCD 的面积＝12×AC×BD ＝12×12×123＝72 3. 25. 解：(1)连接AC ，∵四边形ABCD 是菱形，∴AB ＝BC ，∵∠B ＝60°，∴△ABC 是等边三角形，∵点E 为BC 的中点，∴AE ⊥BC ，∴∠AEC ＝90°，∵∠AEF ＝60°，∴∠FEC ＝90°－60°＝30°，∵∠C ＝180°－∠B ＝120°，∠C ＋∠EFC ＋∠FEC ＝180°， ∴∠EFC ＝30°，∴∠FEC ＝∠EFC ，∴CE ＝CF ，∵BC ＝CD ，∴BC －CE ＝CD －CF ，即BE ＝DF(2)连接AC ，由(1)得△ABC 是等边三角形，∴AB ＝AC ， ∵∠BAE ＋∠EAC ＝60°，∠EAF ＝∠CAF ＋∠EAC ＝60°，∴∠BAE ＝∠CAF ，∵四边形ABCD 是菱形，∠B ＝60°，∴∠ACF ＝12∠BCD ＝∠B ＝60°， ∴△ABE ≌△ACF(ASA)，∴AE ＝AF ， 又∵∠EAF ＝60°，∴△AEF 是等边三角形。

18.2.2菱形同步习题一．选择题1．菱形ABCD的周长为40cm，它的一条对角线长10cm，则它的另一条对角线长为（）A．10cm B．10cm C．5cm D．5cm2．已知平行四边形ABCD，AC，BD是它的两条对角线，那么下列条件中，能判断这个平行四边形为菱形的是（）A．∠BAC＝∠DCA B．∠BAC＝∠DAC C．∠BAC＝∠ABD D．∠BAC＝∠ADB 3．菱形不具备的性质是（）A．对角线一定相等B．对角线互相垂直C．是轴对称图形D．是中心对称图形4．如图，菱形ABCD中，∠D＝135°，BE⊥CD于E，交AC于F，FG⊥BC于G．若△BFG的周长为4，则菱形ABCD的面积为（）A．4B．8C．16D．165．如图，在菱形ABCD中，E、F分别是AB、CD上的点，且AE＝CF，EF与AC相交于点O，连接BO．若∠DAC＝36°，则∠OBC的度数为（）A．36°B．54°C．64°D．72°6．如图，在菱形ABCD中，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，若∠BAD＝70°，则∠CFD等于（）A．50°B．60°C．70°D．80°7．如图，菱形ABCD中，在边AD、BC上分别截取DM＝BN，连接MN交AC于点O，连接DO，若∠BAC＝20°，则∠ODC的度数为（）A．20°B．40°C．50°D．70°8．如图，在菱形ABCD中，AB＝5，对角线BD＝8，过BD的中点O作AD的垂线，交AD 于点E，交BC于点F，连接DF，则DF的长度为（）A．B．C．D．9．如图平行四边形ABCD中，∠A＝110°，AD＝DC．E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠PEF＝（）A．35°B．45°C．50°D．55°10．如图，在菱形ABCD中，∠D＝120°，AB＝2，点E在边BC上，若BE＝2EC，则点B 到AE的距离是（）A．B．C．D．二．填空题11．如图，在▱ABCD中，点E、F分别在边AD，BC上，且DE＝BF，则再添加一个条件：可判定四边形AFCE是菱形．（只添加一个条件）12．在菱形ABCD中，两条对角线相交于点O，且AB＝10cm，AC＝12cm．则菱形ABCD 的面积是cm2．13．如图，菱形ABCD中，AC和BD交于点O，过点D作DE⊥BC于点E，连接OE，若∠BAC＝25°，则∠OED的度数是．14．如图，在菱形ABCD中，AB＝5，AC＝6．过点D作BA的垂线，交BA的延长线于点E，则线段DE的长为．15．如图，菱形ABCD中，EF是AB的垂直平分线，∠FBC＝80°，则∠ACB＝°．三．解答题16．如图，在▱ABCD中，∠ABC＝60°，BC＝2AB，点E、F分别是BC、DA的中点．（1）求证：四边形AECF是菱形；（2）若AB＝2，求BD的长．17．如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC、BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E．（1）求证：四边形ABCD是菱形；（2）若AB＝5，BD＝6，求CE的长．18．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DE∥AC，且2DE＝AC，连接AE交OD于点F，连接DE、OE．（1）求证：AF＝EF；（2）已知AB＝2，若AB＝2DE，求AE的长．参考答案一．选择题1．解：菱形ABCD如右图所示，∵菱形ABCD的周长为40cm，∴AB＝BC＝CD＝AD＝10cm；∵对角线BD＝10cm，∴BO＝DO＝5cm；在Rt△ADO中，AO＝＝＝．∴AD＝2AO＝．故选：A．2．解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAC＝∠ACB，∵∠BAC＝∠DAC，∴∠BAC＝∠ACB，∴AB＝BC，∴四边形ABCD是菱形（邻边相等的平行四边形是菱形）故选：B．3．解：根据菱形的性质可知：菱形的对角线互相垂直平分；菱形既是轴对称图形，又是中心对称图形．进行的对角线相等，而菱形不具备对角线一定相等．故选：A．4．解：∵菱形ABCD中，∠D＝135°，∴∠BCD＝45°，∵BE⊥CD于E，FG⊥BC于G，∴△BFG与△BEC是等腰直角三角形，∵∠GCF＝∠ECF，∠CGF＝∠CEF＝90°，CF＝CF，∴△CGF≌△CEF（AAS），∴FG＝FE，CG＝CE，设BG＝FG＝EF＝x，∴BF＝x，∵△BFG的周长为4，∴x+x+x＝4，∴x＝4﹣2，∴BE＝2，∴BC＝BE＝4，∴菱形ABCD的面积＝4×2＝8，故选：B．5．解：∵四边形ABCD是菱形，∴AB＝BC＝AD＝CD，AB∥CD，AD∥BC，∴∠EAO＝∠FCO，∠DAC＝∠ACB＝36°，在△AOE和△COF中，，∴△AOE≌△COF（AAS），∴AO＝CO，又∵AB＝BC，∴BO⊥AC，∴∠OBC＝90°﹣∠ACB＝54°，故选：B．6．解：连接BF，如图所示：∵四边形ABCD是菱形，∴∠BAC＝∠BAD＝×70°＝35°，∠BCF＝∠DCF＝∠BAC，BC＝DC，∠ABC＝180°﹣∠BAD＝180°﹣70°＝110°，∵EF是线段AB的垂直平分线，∴AF＝BF，∴∠DCF＝∠ABF＝∠BAC＝35°，∴∠CBF＝∠ABC﹣∠ABF＝110°﹣35°＝75°，在△BCF和△DCF中，，∴△BCF≌△DCF（SAS），∴∠CDF＝∠CBF＝75°，∴∠CFD＝180°﹣∠CDF﹣∠DCF＝180°﹣75°﹣35°＝70°，故选：C．7．解：∵四边形ABCD是菱形，∴AB∥CD，∴∠OAM＝∠OCN，在△AOM和△CON中，，∴△AOM≌△CON（AAS），∴OA＝OC，∵四边形ABCD是菱形，∴点O为BD与AC的交点，∵∠ACD＝∠BAC＝20°，∴∠ODC＝90°﹣∠ACD＝70°．故选：D．8．解：连接AC，如图：∵四边形ABCD是菱形，O是BD的中点，∴OD＝OB＝BD＝4，AD＝AB＝5，AC⊥BD，∴OA＝＝3，∵OE⊥AD，∴△AOD的面积＝AD×OE＝OA×OD，∴OE＝＝＝，同理：OF＝，∴EF＝OE+OF＝，∵DE＝＝＝，∵EF⊥AD，∴DF＝＝＝；故选：D．9．解：∵平行四边形ABCD中，AD＝DC，∴四边形ABCD为菱形，∴AB＝BC，∠ABC＝180°﹣∠A＝70°，∵E，F分别为AB，BC的中点，∴BE＝BF，∠BEF＝∠BFE＝55°，∵PE⊥AB，∴∠PEB＝90°∴∠PEF＝90°﹣55°＝35°，故选：A．10．解：过点B作BH⊥AE于点H，过点E作EF⊥AB交AB的延长线于点F，∵菱形ABCD中，AB＝2，∴BC＝2，∵BE＝2EC，∴BE＝，CE＝，∵∠D＝120°，∴∠ABE＝120°，∴∠EBF＝60°，∴BF＝BE＝，EF＝，∴AF＝AB+BF＝2+＝，∴AE＝＝＝，∵S△ABE＝AB•EF，∴BH＝＝＝．故选：A．二．填空题11．解：添加AE＝AF，理由：∵四边形ABCD是平行四边形，∴AD∥BC，且AD＝BC，又∵DE＝BF，∴AE＝FC．∴四边形AFCE是平行四边形．又∵AE＝AF，∴四边形AFCE是菱形．故答案为：AE＝AF．12．解：∵四边形ABCD为菱形，∴AC⊥BD，OA＝OC＝AC＝6cm，OB＝OD，∴OB＝＝＝8（cm），∴BD＝2OB＝16cm，∴S菱形ABCD＝AC•BD＝×12×16＝96（cm2）．故答案为：96．13．解：∵四边形ABCD是菱形，∠BAC＝25°，∴∠ABC＝180°﹣25°﹣25°＝130°，∴O为BD中点，∠DBE＝∠ABC＝65°．∵DE⊥BC，在Rt△BDE中，OE＝BE＝OD，∴∠OEB＝∠OBE＝65°．∴∠OED＝90°﹣65°＝25°．故答案为：25°．14．解：∵四边形ABCD是菱形，AB＝5，AC＝6．∴AB＝BC＝CD＝DA＝5，AC⊥BD，OA＝OC＝3，∴OB＝＝＝4，∴BD＝2OB＝8，∵，∴＝5DE，解得，DE＝，故答案为：．15．解：∵四边形ABCD是菱形，∴AD∥BC，∠DAC＝∠BAC，∴∠AFB＝∠FBC＝80°，∠DAC＝∠ACB，∵EF是AB的垂直平分线，∴AF＝BF，∴∠F AB＝∠FBA＝（180°﹣∠AFB）＝50°，∴∠DAC＝∠BAC＝25°，∴∠ACB＝25°，故答案为：25．三．解答题16．（1）证明：∵四边形ABCD是平行四边形，∴BC∥AD，BC＝AD．∵E，F分别是BC，AD的中点∴BE＝CE＝BC，AF＝AD，∴CE＝AF，CE∥AF，∴四边形AECF是平行四边形，∵BC＝2AB，∴AB＝BE，∵∠ABC＝60°，∴△ABE是等边三角形，∴AE＝BE＝CE，∴平行四边形AECF是菱形；（2）解：作BG⊥AD于G，如图所示：则∠ABG＝90°﹣∠ABC＝30°，∴AG＝AB＝1，BG＝AG＝，∵AD＝BC＝2AB＝4，∴DG＝AG+AD＝5，∴BD＝＝＝2．17．（1）证明：∵AB∥CD，∴∠OAB＝∠DCA，∵AC为∠DAB的平分线，∴∠OAB＝∠DAC，∴∠DCA＝∠DAC，∴CD＝AD，∵AB∥CD，∴四边形ABCD是平行四边形，∵AD＝AB，∴▱ABCD是菱形；（2）解：∵四边形ABCD是菱形，∴OA＝OC，BD⊥AC，OB＝OD＝BD＝3，∴OA＝＝＝4，∴AC＝2OA＝8，∴菱形ABCD的面积＝AC×BD＝×8×6＝24，∵CE⊥AB，∴菱形ABCD的面积＝AB×CE＝5CE＝24，∴CE＝．18．（1）证明：∵四边形ABCD是菱形，∴OA＝OC＝AC，∵2DE＝AC，∴DE＝OA，又∵DE∥AC，∴四边形OADE是平行四边形，∴AF＝EF；（2）解：连接CE，∵DE∥OC，DE＝OC，∴四边形OCED是平行四边形，又∵菱形ABCD，∴AC⊥BD，∴四边形OCED是矩形，∴∠OCE＝90°，又∵AB＝2DE＝AC，∴△ABC为等边三角形，∵在菱形ABCD中，∠ABC＝60°，∴AC＝AB＝2，AO＝AC＝1，∴在矩形OCED中，CE＝OD＝＝，∴在Rt△ACE中，AE＝＝．。

2020春人教版八下数学18.2.2菱形同步课堂练习(学生版)第1课时菱形的性质01基础题知识点1菱形的性质1．(2018·十堰)菱形不具备的性质是()A．四条边都相等B．对角线一定相等C．是轴对称图形D．是中心对称图形2．(2019·河北)如图，在菱形ABCD中，∠D＝150°，则∠1＝()A．30°B．25°C．20°D．15°3．(2019·贵阳)如图，菱形ABCD的周长是4 cm，∠ABC＝60°，那么这个菱形的对角线AC的长是() A．1 cm B．2 cmC．3 cm D．4 cm4．(2019·呼和浩特)已知菱形的边长为3，较短的一条对角线的长为2，则该菱形较长的一条对角线的长为() A．2 2 B．2 5 C．4 2 D．2105．(2019·赤峰)如图，菱形ABCD周长为20，对角线AC，BD相交于点O，E是CD的中点，则OE的长是()A．2.5B．3C．4D．56．(2019·衢州)已知：如图，在菱形ABCD中，点E，F分别在边BC，CD上，且BE＝DF，连接AE，AF.求证：AE＝AF.知识点2菱形的面积7．(2018·徐州)若菱形两条对角线的长分别是6 cm和8 cm，则其面积为cm2.8．(教材P56例3变式)如图，四边形ABCD是菱形，对角线AC，BD相交于点O，且∠ACD＝30°，BD＝4，求菱形ABCD的面积．易错点点的位置不确定导致漏解9．四边形ABCD是菱形，∠BAD＝60°，AB＝6，对角线AC与BD相交于点O，点E在AC上．若OE＝3，则CE的长为．02中档题10．(2019·泸州)一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为()A．8 B．12 C．16 D．3211．如图，在菱形ABCD中，点M，N分别在AB，CD上，且AM＝CN，MN与AC交于点O，连接BO.若∠DAC＝28°，则∠OBC的度数为()A．28°B．52°C．62°D．72°12．(2019·绵阳)如图，在平面直角坐标系中，四边形OABC为菱形，O(0，0)，A(4，0)，∠AOC＝60°，则对角线交点E的坐标为()A．(2，3) B．(3，2) C．(3，3) D．(3，3)13．(2019·广西)如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AH⊥BC于点H，已知BO＝4，S菱形ABCD＝24，则AH＝．14．(2019·百色)如图，在菱形ABCD中，作BE⊥AD，CF⊥AB，分别交AD，AB的延长线于点E，F.(1)求证：AE＝BF；(2)若点E恰好是AD的中点，AB＝2，求BD的值．15．如图，在菱形ABCD中，对角线AC，BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E.(1)求证：四边形ACDE是平行四边形；(2)若AC＝8，BD＝6，求△ADE的周长．03综合题16．如图，已知菱形ABCD的周长为16，面积为83，E为AB的中点．若P为对角线BD上一动点，则EP ＋AP的最小值为．17．(2019·宁波)如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD 的对角线BD上．(1)求证：BG＝DE；(2)若E为AD中点，FH＝2，求菱形ABCD的周长．对角线互相垂直的四边形的面积我们已经知道：菱形的面积等于对角线乘积的一半，那么，如果是对角线互相垂直的任意一个四边形，还有这样的结论吗？如图，四边形ABCD的对角线AC，BD互相垂直，其中对角线BD长为15，AC长为20，垂足为O，求四边形ABCD的面积．(请写出求解过程)结论：对角线互相垂直的四边形的面积等于．第2课时菱形的判定01基础题知识点1有一组邻边相等的平行四边形是菱形1．如图，若要使▱ABCD成为菱形，则可添加的条件是()A．AB＝CDB．AD＝BCC．AB＝BCD．AC＝BD2．如图，在△ABC中，AD是∠BAC的平分线，DE∥AC交AB于点E，DF∥AB交AC于点F，求证：四边形AEDF是菱形．知识点2对角线互相垂直的平行四边形是菱形3．如图，四边形ABCD的对角线互相垂直，且满足AO＝CO，请你添加一个适当的条件，使四边形ABCD成为菱形．(只需添加一个即可)4．(2018·遂宁)如图，在▱ABCD中，点E，F分别是AD，BC上的点，且DE＝BF，AC⊥EF.求证：四边形AECF 是菱形．知识点3四条边相等的四边形是菱形5．(2019·兰州)如图，AC＝8，分别以A，C为圆心，以5为半径作弧，两条弧分别相交于点B，D.依次连接A，B，C，D，连接BD交AC于点O.(1)判断四边形ABCD的形状，并说明理由；(2)求BD的长．6．如图，在四边形ABCD中，AC＝BD，E，F，G，H依次是AB，BC，CD，DA的中点．求证：四边形EFGH 是菱形．易错点对菱形的判定方法掌握不透导致出错7．下列命题：①四边都相等的四边形是菱形；②两组邻边分别相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形；④对角线相等的四边形是菱形；⑤一条对角线平分一组对角的平行四边形是菱形．其中正确的是．(填序号)02中档题8．(2019·宁夏)如图，四边形ABCD的两条对角线相交于点O，且互相平分．添加下列条件，仍不能判定四边形ABCD为菱形的是()A．AC⊥BD B．AB＝ADC．AC＝BD D．∠ABD＝∠CBD9．(2019·永州)如图，四边形ABCD的对角线相交于点O，且点O是BD的中点．若AB＝AD＝5，BD＝8，∠ABD ＝∠CDB，则四边形ABCD的面积为()A．40 B．24 C．20 D．1510．如图，在四边形ABCD中，AB＝AD，BC＝DC，AC，BD相交于点O，点E在AO上，且OE＝OC.(1)求证：∠1＝∠2；(2)连接BE，DE，判断四边形BCDE的形状，并说明理由．11．(2019·宿迁)如图，矩形ABCD中，AB＝4，BC＝2，点E，F分别在AB，CD上，且BE＝DF＝3 2.(1)求证：四边形AECF是菱形；(2)求线段EF的长．03综合题12．(2019·滨州)如图，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG.(1)求证：四边形CEFG是菱形；(2)若AB＝6，AD＝10，求四边形CEFG的面积．2020春人教版八下数学18.2.2菱形同步课堂练习(教师版)第1课时菱形的性质01基础题知识点1菱形的性质1．(2018·十堰)菱形不具备的性质是(B)A．四条边都相等B．对角线一定相等C．是轴对称图形D．是中心对称图形2．(2019·河北)如图，在菱形ABCD中，∠D＝150°，则∠1＝(D)A．30°B．25°C．20°D．15°3．(2019·贵阳)如图，菱形ABCD的周长是4 cm，∠ABC＝60°，那么这个菱形的对角线AC的长是(A)A．1 cm B．2 cmC．3 cm D．4 cm4．(2019·呼和浩特)已知菱形的边长为3，较短的一条对角线的长为2，则该菱形较长的一条对角线的长为(C) A．2 2 B．2 5 C．4 2 D．2105．(2019·赤峰)如图，菱形ABCD周长为20，对角线AC，BD相交于点O，E是CD的中点，则OE的长是(A)A．2.5B．3C．4D．56．(2019·衢州)已知：如图，在菱形ABCD中，点E，F分别在边BC，CD上，且BE＝DF，连接AE，AF.求证：AE＝AF.证明：∵四边形ABCD是菱形，∴AB＝AD，∠B＝∠D.∵BE＝DF，∴△ABE≌△ADF(SAS)．∴AE＝AF.知识点2菱形的面积7．(2018·徐州)若菱形两条对角线的长分别是6 cm和8 cm，则其面积为24cm2.8．(教材P56例3变式)如图，四边形ABCD是菱形，对角线AC，BD相交于点O，且∠ACD＝30°，BD＝4，求菱形ABCD的面积．解：∵四边形ABCD 是菱形，BD ＝4，∴OA ＝OC ＝12AC ，OB ＝OD ＝12BD ＝2，AC ⊥BD.∵在Rt △OCD 中，∠OCD ＝30°， ∴CD ＝2OD ＝4，OC ＝CD 2－OD 2＝42－22＝2 3.∴AC ＝2OC ＝4 3.∴S 菱形ABCD ＝12AC·BD ＝12×43×4＝8 3.易错点 点的位置不确定导致漏解9．四边形ABCD 是菱形，∠BAD ＝60°，AB ＝6，对角线AC 与BD 相交于点O ，点E 在AC 上．若OE ＝3，则CE 的长为02 中档题 10．(2019·泸州)一个菱形的边长为6，面积为28，则该菱形的两条对角线的长度之和为(C ) A ．8 B ．12 C ．16 D ．3211．如图，在菱形ABCD 中，点M ，N 分别在AB ，CD 上，且AM ＝CN ，MN 与AC 交于点O ，连接BO.若∠DAC ＝28°，则∠OBC 的度数为(C )A ．28°B ．52°C ．62°D ．72°12．(2019·绵阳)如图，在平面直角坐标系中，四边形OABC 为菱形，O(0，0)，A(4，0)，∠AOC ＝60°，则对角线交点E 的坐标为(D )A ．(2，3)B ．(3，2)C ．(3，3)D ．(3，3)13．(2019·广西)如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，过点A 作AH ⊥BC 于点H ，已知BO ＝4，S 菱形ABCD ＝24，则AH ＝245．14．(2019·百色)如图，在菱形ABCD 中，作BE ⊥AD ，CF ⊥AB ，分别交AD ，AB 的延长线于点E ，F. (1)求证：AE ＝BF ；(2)若点E 恰好是AD 的中点，AB ＝2，求BD 的值．解：(1)证明：∵四边形ABCD 是菱形， ∴AB ＝BC ，AD ∥BC.∴∠A＝∠CBF.∵BE⊥AD，CF⊥AB，∴∠AEB＝∠BFC＝90°.∴△AEB≌△BFC(AAS)．∴AE＝BF.(2)∵点E是AD的中点，且BE⊥AD，∴直线BE为AD的垂直平分线．∴BD＝AB＝2.15．如图，在菱形ABCD中，对角线AC，BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E.(1)求证：四边形ACDE是平行四边形；(2)若AC＝8，BD＝6，求△ADE的周长．解：(1)证明：∵四边形ABCD是菱形，∴AB∥CD，AC⊥BD.∴AE∥CD.又∵DE⊥BD，∴DE∥AC.∴四边形ACDE是平行四边形．(2)∵四边形ABCD是菱形，AC＝8，BD＝6，∴AO＝4，DO＝3，AD＝CD＝AO2＋DO2＝5.∵四边形ACDE是平行四边形，∴AE＝CD＝5，DE＝AC＝8.∴C△ADE＝AD＋AE＋DE＝5＋5＋8＝18.03综合题16．如图，已知菱形ABCD的周长为16，面积为83，E为AB的中点．若P为对角线BD上一动点，则EP＋AP的最小值为17．(2019·宁波)如图，矩形EFGH的顶点E，G分别在菱形ABCD的边AD，BC上，顶点F，H在菱形ABCD 的对角线BD上．(1)求证：BG＝DE；(2)若E为AD中点，FH＝2，求菱形ABCD的周长．解：(1)证明：∵四边形EFGH是矩形，∴EH＝FG，EH∥FG.∴∠GFH＝∠EHF.∵∠BFG＝180°－∠GFH，∠DHE＝180°－∠EHF，∴∠BFG＝∠DHE.∵四边形ABCD是菱形，∴AD∥BC.∴∠GBF＝∠EDH.∴△BGF≌△DEH(AAS)．∴BG＝DE.(2)连接EG，∵四边形ABCD是菱形，∴AD＝BC，AD∥BC.∵E为AD中点，∴AE＝ED.∵BG＝DE，∴AE＝BG，AE∥BG.∴四边形ABGE是平行四边形．∴AB＝EG.∵在矩形EFGH中，EG＝FH＝2，∴AB＝2.∴菱形ABCD的周长为8.对角线互相垂直的四边形的面积我们已经知道：菱形的面积等于对角线乘积的一半，那么，如果是对角线互相垂直的任意一个四边形，还有这样的结论吗？如图，四边形ABCD的对角线AC，BD互相垂直，其中对角线BD长为15，AC长为20，垂足为O，求四边形ABCD的面积．(请写出求解过程)解：∵S四边形ABCD＝S△ADC＋S△BAC＝12AC·OD＋12AC·BO＝12AC·(OD＋OB)＝12AC·BD，∴S四边形ABCD＝12×20×15＝150.结论：对角线互相垂直的四边形的面积等于两条对角线乘积的一半．第2课时菱形的判定01基础题知识点1有一组邻边相等的平行四边形是菱形1．如图，若要使▱ABCD成为菱形，则可添加的条件是(C)A．AB＝CDB．AD＝BCC．AB＝BCD．AC＝BD2．如图，在△ABC中，AD是∠BAC的平分线，DE∥AC交AB于点E，DF∥AB交AC于点F，求证：四边形AEDF是菱形．证明：∵DE∥AC，DF∥AB，∴四边形AEDF为平行四边形，∠FAD＝∠EDA.∵AD是∠BAC的平分线，∴∠EAD＝∠FAD.∴∠EDA＝∠EAD.∴AE＝ED.∴四边形AEDF是菱形．知识点2对角线互相垂直的平行四边形是菱形3．如图，四边形ABCD的对角线互相垂直，且满足AO＝CO，请你添加一个适当的条件BO＝DO(答案不唯一)，使四边形ABCD成为菱形．(只需添加一个即可)4．(2018·遂宁)如图，在▱ABCD中，点E，F分别是AD，BC上的点，且DE＝BF，AC⊥EF.求证：四边形AECF 是菱形．证明：∵四边形ABCD是平行四边形，∴AD綊BC.∵DE＝BF，∴AD－DE＝BC－BF，即AE＝FC.∵AE∥FC，∴四边形AECF是平行四边形．又∵AC⊥EF，∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形)．知识点3四条边相等的四边形是菱形5．(2019·兰州)如图，AC＝8，分别以A，C为圆心，以5为半径作弧，两条弧分别相交于点B，D.依次连接A，B，C，D，连接BD交AC于点O.(1)判断四边形ABCD的形状，并说明理由；(2)求BD的长．解：(1)四边形ABCD 为菱形，理由如下：由作法得AB ＝AD ＝CB ＝CD ＝5，∴四边形ABCD 为菱形．(2)∵四边形ABCD 为菱形，∴OA ＝OC ＝12AC ＝4，OB ＝OD ，AC ⊥BD. 在Rt △AOB 中，OB ＝52－42＝3，∴BD ＝2OB ＝6.6．如图，在四边形ABCD 中，AC ＝BD ，E ，F ，G ，H 依次是AB ，BC ，CD ，DA 的中点．求证：四边形EFGH 是菱形．证明：∵E ，F ，G ，H 分别是线段AB ，BC ，CD ，AD 的中点，∴EH ，FG 分别是△ABD ，△BCD 的中位线，EF ，HG 分别是△ABC ，△ACD 的中位线．∴EH ＝FG ＝12BD ，EF ＝HG ＝12AC. 又∵AC ＝BD ，∴EH ＝FG ＝EF ＝HG.∴四边形EFGH 是菱形．易错点 对菱形的判定方法掌握不透导致出错7．下列命题：①四边都相等的四边形是菱形；②两组邻边分别相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形；④对角线相等的四边形是菱形；⑤一条对角线平分一组对角的平行四边形是菱形．其中正确的是①③⑤．(填序号)02中档题8．(2019·宁夏)如图，四边形ABCD的两条对角线相交于点O，且互相平分．添加下列条件，仍不能判定四边形ABCD为菱形的是(C)A．AC⊥BD B．AB＝ADC．AC＝BD D．∠ABD＝∠CBD9．(2019·永州)如图，四边形ABCD的对角线相交于点O，且点O是BD的中点．若AB＝AD＝5，BD＝8，∠ABD ＝∠CDB，则四边形ABCD的面积为(B)A．40 B．24 C．20 D．1510．如图，在四边形ABCD中，AB＝AD，BC＝DC，AC，BD相交于点O，点E在AO上，且OE＝OC.(1)求证：∠1＝∠2；(2)连接BE，DE，判断四边形BCDE的形状，并说明理由．解：(1)证明：在△ADC 和△ABC 中，⎩⎨⎧AD ＝AB ，AC ＝AC ，DC ＝BC ，∴△ADC ≌△ABC(SSS )．∴∠1＝∠2.(2)四边形BCDE 是菱形．理由：∵∠1＝∠2，CD ＝BC ，∴AC 垂直平分BD.∵OE ＝OC ，∴四边形DEBC 是平行四边形．∵AC ⊥BD ，∴四边形DEBC 是菱形．11．(2019·宿迁)如图，矩形ABCD 中，AB ＝4，BC ＝2，点E ，F 分别在AB ，CD 上，且BE ＝DF ＝32. (1)求证：四边形AECF 是菱形；(2)求线段EF 的长．解：(1)证明：∵在矩形ABCD 中，AB ＝4，BC ＝2，∴CD ＝AB ＝4，AD ＝BC ＝2，CD ∥AB ，∠D ＝∠B ＝90°.∴AF ＝CE ＝22＋（32）2＝52. ∵BE ＝DF ＝32，∴CF ＝AE ＝4－32＝52. ∴AF ＝CF ＝CE ＝AE ＝52. ∴四边形AECF 是菱形．(2)过点F 作FH ⊥AB 于点H ，则四边形AHFD 是矩形，∴AH ＝DF ＝32，FH ＝AD ＝2. ∴EH ＝52－32＝1. ∴EF ＝FH 2＋HE 2＝22＋12＝ 5.03 综合题12．(2019·滨州)如图，矩形ABCD 中，点E 在边CD 上，将△BCE 沿BE 折叠，点C 落在AD 边上的点F 处，过点F 作FG ∥CD 交BE 于点G ，连接CG .(1)求证：四边形CEFG 是菱形；(2)若AB ＝6，AD ＝10，求四边形CEFG 的面积．解：(1)证明：由题意得△BCE ≌△BFE ，∴∠BEC ＝∠BEF ，FE ＝CE.∵FG ∥CE ，∴∠FGE ＝∠CEB.∴∠FGE ＝∠FEG.∴FG ＝FE.∴FG ＝EC.∴四边形CEFG 是平行四边形．又∵CE ＝FE ，∴四边形CEFG 是菱形．(2)∵矩形ABCD 中，AB ＝6，AD ＝10，BC ＝BF ，∴∠BAF ＝90°，AD ＝BC ＝BF ＝10.∴AF ＝8.∴DF ＝2.设EF ＝x ，则CE ＝x ，DE ＝6－x.∵∠FDE ＝90°，∴22＋(6－x)2＝x 2.解得x ＝103. ∴CE ＝103. ∴S 四边形CEFG ＝CE·DF ＝103×2＝203.。

矩形、菱形的性质定理和判定定理及其证明习题精选矩形的性质和判定1．矩形的两条对角线的夹角为60°，一条对角线与短边的和为15，则短边的和为15，则短边的长是________。

2．如图32-3-1，设矩形ABCD和矩形AEFC的面积分别为S1、S2，则二者的大小关系是：S1____S2。

3．如果矩形一个角的平分线分一边为4 cm和3 cm两部分，那么矩形的周长为_______。

4．现有一张长为40cm, 宽为20 cm的长方形纸片（如图32-3-2所示），要从中剪出长为18 cm，宽为12 cm的长方形纸片，则最多能剪出___张。

5．矩形的一条较短边的长为5 c m，两条对角线的夹角为60°，则它的对角线的长等于_____ cm。

6．如图32-3-3，在矩形ABCD中，CE⊥BD于E，∠DCE：∠ECB=3：1，则∠ACE=____度。

7．下列说法中正确的是( )A．一个角是直角，两条对角线相等的四边形是矩形。

B．一组对边平行且有一个角是直角的四边形是矩形。

C．对角线互相垂直的平行四边开是矩形。

D．一个角是直角且对角线互相平分的四边形是矩形。

8．四边形ABCD的对角线相交于O，在下列条件中，不能说明它为矩形的是（）A．AB=CD,AD=BC, BAD=90°B．AO=CO，BO=DO，AC=BDC．∠BAD=∠ABC=90°, ∠BAD+∠ADC=180°D．∠BAD=∠BCD, ∠ABC+∠ADC=180°★菱形的性质和判定9．己知菱形的锐角是60°，边长是20 cm，则较长对角线是_____。

10．菱形两条对角线的长分别为6 cm和8 cm，它的高为______。

11．菱形的一个内角是120°，平分这个内角的一条对角钱长为13 cm，则菱形的周长是____。

12．菱形的一边与两条对角线所构成的两个角的差是32°，则菱形较小的内角是_____。

18.2.2菱形同步练习一．选择题1．平行四边形、矩形、菱形都具有的性质是（）A．对角线相等B．对角线互相平分C．都是轴对称图形D．对角线互相垂直2．菱形ABCD的边长是5cm，一条对角线AC的长是8cm，则此菱形的面积为（）A．40cm2B．48cm2C．24cm2D．24cm23．已知菱形的周长是高的8倍，则菱形的两邻角的度数之比为（）A．3：1B．4：1C．5：1D．6：14．如图，菱形ABCD中，∠A＝50°，DE⊥AB于点E．则∠BDE的度数为（）A．25°B．35°C．40°D．50°5．如图，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，垂足为E．连接DF，则∠DFE等于（）A．150°B．140°C．130°D．120°6．如图，在菱形ABCD中，AB＝5，BD＝6，DE⊥AB于点E，则DE的长为（）A．4.8B．5C．9.6D．107．如图，菱形ABCD和菱形ECGF的边长分别为4和2，∠B＝120°，则图中阴影部分的面积是（）A．3B．2C．4D．38．如图，在菱形ABCD中，对角线AC，BD相交于点O，BD＝6，AC＝8，直线OE⊥AB交CD 于点F，则EF的长为（）A．4.8B．C．5D．69．如图，菱形ABCD的对角线相交于点O，AC＝12，BD＝16，点P为边BC上一点，且P不与B、C重合．过P作PE⊥AC于E，PF⊥BD于F，连接EF，则EF的最小值为（）A．4B．4.8C．5D．610．如图，在菱形ABCD中，∠A＝60°，E、F分别是AB，AD的中点，DE、BF相交于点G，连接BD，CG．有下列结论：①∠BGD＝120°；②BG+DG＝CG；③△BDF≌△CGB；④S＝AB2；⑤2DE＝DC；⑥BF＝BC，正确结论的有（）个．菱形ABCDA．1B．2C．3D．4二．填空题11．如图，四边形ABCD的对角线AC与BD交于点O，AC⊥BD，且AC平分BD，若添加一个条件，则四边形ABCD为菱形．12．若一个菱形的周长为200cm，一条对角线长为60cm，则它的面积为．13．如图，菱形ABCD的边长AB＝3，对角线BD＝4，点E，F在BD上，且BE＝DF＝，连接AE，AF，CE，CF．则四边形AECF的周长为．14．如图，菱形ABCD的对角线AC，BD相交于点O，过点O作OE⊥BC于点E，若AC＝6，BD＝8，则OE＝．15．如图，在菱形ABCD中，∠B＝60°，E，H分别为AB，BC的中点，G，F分别为线段HD，CE的中点．若线段FG的长为2，则AB的长为．三．解答题16．如图，在菱形ABCD中，E为对角线BD上一点，且AE＝DE，连接CE．（1）求证：CE＝DE．（2）当BE＝2，CE＝1时，求菱形的边长．17．如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE 的延长线于F，连接CF．（1）求证：△AEF≌△DEB；（2）若∠BAC＝90°，求证：四边形ADCF是菱形．18．如图，平行四边形ABCD中，E、F分别为CD、BC上两点，AF平分∠BAE，∠EAD＝∠FEC．（1）求证：AB＝AE；（2）若∠B＝90°，AF与DC的延长线交于点H，求证：四边形ABHE为菱形．参考答案一．选择题1．解：平行四边形的对角线互相平分，而对角线相等、是轴对称图形、互相垂直不一定成立．故平行四边形、矩形、菱形都具有的性质是：对角线互相平分．故选：B．2．解：如图所示：∵菱形ABCD的边长为5cm，对角线AC＝8cm，∴AB＝5cm，AO＝CO＝4cm，OB＝OD，AC⊥BD，∴OB＝＝＝3（cm），∴BD＝2OB＝6cm，∴此菱形的面积为×8×6＝24（cm2）．故选：D．3．解：如图所示：∵四边形ABCD是菱形，菱形的周长是高的8倍，∴AB＝BC＝CD＝DA＝2，∠DAB+∠B＝180°，∵AE＝1，AE⊥BC，∴AE＝AB，∴∠B＝30°，∴∠DAB＝150°，∴∠DAB：∠B＝5：1，故选：C．4．解：∵四边形ABCD是菱形，∠A＝50°，∴AD＝AB，∴∠ADB＝65°，∵DE⊥AB，∴∠ADE＝90°﹣50°＝40°，∴∠BDE＝65°﹣40°＝25°，故选：A．5．解：连接BF，如图所示：∵四边形ABCD是菱形，∠BAD＝80°，∴∠BAC＝∠BAD＝×80°＝40°，AB＝BC＝DC，∠BCF＝∠DCF＝∠BAC＝40°，∠ABC＝180°﹣∠BAD＝100°，∵EF是线段AB的垂直平分线，∴AF＝BF，∠AFE＝90°﹣∠BAC＝50°，∴∠ABF＝∠BAC＝40°∴∠CBF＝∠ABC﹣∠ABF＝100°﹣40°＝60°，在△BCF和△DCF中，，∴△BCF≌△DCF（SAS），∴∠CDF＝∠CBF＝60°，∴∠AFD＝∠CDF+∠DCF＝60°+40°＝100°，∴∠DFE＝∠AFD+∠AFE＝150°；故选：A．6．解：∵四边形ABCD为菱形，∴AO＝CO，BO＝DO＝3，AC⊥BD，∴AO＝＝＝4，∴AC＝8，∴S菱形ABCD＝AC•BD＝×8×6＝24，∵DE⊥AB，∴S菱形ABCD＝AB•DE＝5DE，∴5DE＝24，∴DE＝＝4.8，故选：A．7．解：方法一：如图，连接AC，则AC平行EG，根据平行线间的距离处处相等可知：阴影部分的面积＝三角形ECG的面积＝菱形ECGF的面积＝3．方法二：如图，设AG交CE于点H，∵菱形ABCD的边AB∥CD，∴△GCH∽△GBA，∴CH：AB＝GC：GB，即CH：4＝2：6，解得CH＝，所以，EH＝CE﹣CH＝2﹣＝，∵∠B＝120°，∴∠BCD＝∠FEC＝180°﹣120°＝60°，∴点B到CD的距离为4×＝6，点F到CE的距离为2×＝3，∴阴影部分的面积＝S△AEH+S△GEH＝××（6+3）＝3．故选：D．8．解：∵在菱形ABCD中，BD＝6，AC＝8，∴OB＝BD＝3，OA＝AC＝4，AC⊥BD，∴AB＝＝5，∵S菱形ABCD＝AC•BD＝AB•EF，即×6×8＝5EF，∴EF＝4.8．故选：A．9．解：连接OP，∵四边形ABCD是菱形，AC＝12，BD＝16，∴AC⊥BD，BO＝BD＝8，OC＝AC＝6，∴BC＝＝＝10，∵PE⊥AC，PF⊥BD，AC⊥BD，∴四边形OEPF是矩形，∴FE＝OP，∵当OP⊥BC时，OP有最小值，此时S△OBC＝OB×OC＝BC×OP，∴OP＝＝4.8，∴EF的最小值为4.8，故选：B．10．解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD．∠A＝∠BCD．∵∠A＝60°，∴∠BCD＝60°，∴△ABD是等边三角形，△BDC是等边三角形．∴∠ADB＝∠ABD＝60°，∠CDB＝∠CBD＝60°．∵E，F分别是AB，AD的中点，∴∠BFD＝∠DEB＝90°，∴∠GDB＝∠GBD＝30°，∴∠GDC＝∠GBC＝90°，DG＝BG，∴∠BGD＝360°﹣90°﹣90°﹣60°＝120°，故①正确；在△CDG和△CBG中，，∴△CDG≌△CBG（SSS），∴∠DGC＝∠BGC＝60°．∴∠GCD＝30°，∴CG＝2GD＝GD+GD，∴CG＝DG+BG．故②正确．∵△GBC为直角三角形，∴CG＞BC，∴CG≠BD，∴△BDF与△CGB不全等．故③错误；∵S菱形ABCD＝2S△ADB＝2×AB•DE＝AB•（BE）＝AB•AB＝AB2，故④错误；∵DE＝BE＝AB＝CD，∴2DE＝CD，故⑤正确；∵BD＞BF，BD＝BC，∴BC＞BF，故⑥错误．∴正确的有：①②⑤共三个．故选：C．二．填空题11．解：添加一个条件OA＝OC，则四边形ABCD为菱形，理由如下：∵AC平分BD，OA＝OC，∴四边形ABCD是平行四边形，又∵AC⊥BD，∴平行四边形ABCD是菱形，故答案为：OA＝OC（答案不唯一）．12．解：已知AC＝60cm，菱形对角线互相垂直平分，∴AO＝30cm，又∵菱形ABCD周长为200cm，∴AB＝50cm，∴BO＝＝＝40cm，∴AC＝2BO＝80cm，∴菱形的面积为×60×80＝2400（cm2）．故答案为：2400cm2．13．解：如图，连接AC，交BD于O，∵四边形ABCD是菱形，∴AC⊥BD，BO＝BD＝＝，在Rt△ABO中，AO＝＝＝1，又∵BE＝，∴EO＝﹣＝，在Rt△AOE中，AE＝＝＝，同理可得，CE＝CF＝AF＝，∴四边形AECF的周长4．故答案为：4．14．解：∵菱形ABCD中，AC＝6，BD＝8，∴OA＝OC＝AC＝3，OB＝BD＝4，AC⊥BD，∴BC＝＝＝5，∵OE⊥BC，∴S△OBC＝×OB×OC＝×BC×OE，∴OE＝＝＝，故答案为：．15．解：如图，连接CG并延长，交AD于点M，连接EM，∵四边形ABCD为菱形，∠B＝60°，∴AD∥BC，∴∠A＝120°，∠MGD＝∠CGH，∵点G为HD的中点，∴HG＝DG，∵∠MGD＝∠CGH，∴△MGD≌△CGH（ASA），∴MG＝CG，MD＝CH＝BC＝AD，∴点G为MC的中点，点M为AD的中点，∵F，G分别为CE和CM的中点，∴FG是△CEM的中位线，∴FG＝EM，∴EM＝2FG＝4，∵E，M分别为AB和AD的中点，∴AE＝AM，∵∠A＝120°，∴EM＝AE＝4，∴AE＝4，∴AB＝2AE＝8．故答案为：8．三．解答题16．（1）证明：∵四边形ABCD是菱形，∴∠ABE＝∠CBE，AB＝CB，在△ABE和△CBE中，，∴△ABE≌△CBE（SAS），∴AE＝CE，∵AE＝DE，∴CE＝DE；（2）解：如图，连接AC交BD于H，∵四边形ABCD是菱形，∴AH⊥BD，BH＝DH，AH＝CH，∵CE＝DE＝AE＝1，∴BD＝BE+DE＝2+1＝3，∴BH＝BD＝，EH＝BE﹣BH＝2﹣＝，在Rt△AHE中，由勾股定理得：AH＝＝＝，在Rt△AHB中，由勾股定理得：AB＝＝＝，∴菱形的边长为．17．证明：（1）∵E是AD的中点，∴AE＝DE，∵AF∥BC，∴∠AFE＝∠DBE，∵∠AEF＝∠DEB，∴△AEF≌△DEB；（2）∵△AEF≌△DEB，∴AF＝DB，∵AD是BC边上的中线，∴DC＝DB，∴AF＝DC，∵AF∥DC，∴四边形ADCF是平行四边形，∵∠BAC＝90°，AD是BC边上的中线，∴AD＝DC，∴▱ADCF是菱形．18．（1）证明：∵∠AEC＝∠AEF+∠FEC＝∠EAD+∠D，∠EAD＝∠FEC，∴∠AEF＝∠D，∵四边形ABCD是平行四边形，∴∠B＝∠D，∴∠B＝∠AEF，∵AF平分∠BAE，∴∠BAF＝∠EAF，在△ABF和△AEF中，，∴△ABF≌△AEF（AAS），∴AB＝AE；（2）证明：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠BAF＝∠EHA，∵∠BAF＝∠EAF，∴∠EHA＝∠EAF，∴AE＝HE，∵AB＝AE，∴AB＝EH，∴四边形ABHE是平行四边形，又∵AB＝AE，∴四边形ABHE为菱形．。