有理数的运算专项训练

有理数计算技巧专项训练
1. 有理数计算中，正负号可别弄混啦！就像你走路不能左右不分呀！比如计算 -3+5，可别看成 3+5 哦！
2. 约分可是个厉害的技巧呢！想想看，就像把一大块蛋糕合理分配，变得更简洁好吃一样。

比如 4/8 约分后就是 1/2 啦！
3. 加减混合运算有妙招哦！这就好比是一场有趣的排列游戏呢。

试着算一算5-3+2 呀！
4. 乘法分配律呀，那可太重要啦！就如同给数字们穿上合适的衣服一样合适。

计算3×(4+5)，用起来呀！
5. 分数计算也不难呀，耐心点就好啦！就好像拼图一样，一块一块来。

算算1/3 + 1/4 呗！
6. 负数计算别害怕呀！可以想象成是在走相反的路哦。

算一算 -2×3 是多少呢！
7. 混合运算要按顺序来，可别乱来哟！这就像排队一样要有秩序。

来算算
2+3×4 呀！
8. 转换成分数来计算有时超好用呢！好比是给数字换个装扮呢。

试试把转
换成分数计算呀！
9. 多练练有理数计算技巧专项训练，你会发现数学其实超有趣的啦！就像打游戏升级一样有成就感哦！总之，掌握了这些技巧，有理数计算就不再是难题啦！。

第1章有理数（易错必刷30题11种题型专项训练）一．正数和负数（共5小题）1．（2022秋•定远县校级月考）某品牌大米包装袋上印有【（9±0.10）（kg）】字样．即标准重量为9kg，上下偏差不超过0.1kg就符合标准．则下列不符合标准的是（）A．9.15kg B．8.95kg C．9.05kg D．8.90kg2．（2022秋•怀远县校级月考）在﹣3.5，﹣2.1，0，﹣1，﹣4，5这6个数中，负数有几个（）A．1B．2C．3D．43．（2022秋•南陵县期中）若a是有理数，则下列叙述正确的是（）A．|a|一定是正数B．﹣a一定是负数C．﹣|a|可能是0D．﹣|a|一定是负数4．（2022秋•怀远县校级月考）若规定向东为正，则向东走100m记作m，向西走200m记作m．5．（2022秋•颍州区校级期末）2020年国庆节放假八天，高速公路免费通行，各地风景区游人如织其中，其中闻名于世的北京故宫，在10月1日的游客人数就已经达到了5万人，接下来的七天中，每天的游客人数变化（单位：万人）如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）．日期10月2日10月3日10月4日10月5日10月6日10月7日10月8日人数变化+0.6+0.2+0.1﹣0.2﹣0.8﹣1.6﹣0.1（1）10月3日的人数为万人；（2）这八天，游客人数最多的是10月日，达到万人；游客人数最少的是10月日，为万人；（3）这8天参观故宫的总人数为万人；（4）如果你们一家人打算在下一个国庆节参观故宫，请你对你们的出行日期提一个建议．二．有理数（共2小题）6．（2022秋•蚌山区校级月考）下列叙述正确的是（）A．不是正数的数一定是负数B．正有理数包括整数和分数C．整数不是正整数就是负整数D．有理数绝对值越大，离原点越远7．（2022秋•霍邱县校级月考）在﹣，，﹣π，﹣4中，属于负整数的是（）A．﹣B．C．﹣πD．﹣4三．数轴（共4小题）8．（2021秋•蚌埠期末）如图，在数轴上有A、B两个动点，O为坐标原点．点A、B从图中所示位置同时向数轴的负方向运动，A点运动速度为每秒2个单位长度，B点运动速度为每秒3个单位长度，当运动秒时，点O恰好为线段AB的中点．9．（2021秋•定远县校级期末）已知a，b在数轴上的位置如图所示，则化简|a﹣b|+|a+b|的结果是．10．（2021秋•庐阳区期末）如图，点A在数轴上表示的数是﹣9，点D在数轴上表示的数是12，AB＝4（单位长度），CD＝2（单位长度）．（1）则点B在数轴上表示的数是，点C在数轴上表示的数是，线段BC的长＝（单位长度）；（2）若点P是线段BC的中点，则P点在数轴上表示的数是：；（3）若点Q是坐标轴上的点，且QC＝2QB，则Q点在数轴上表示的数是．11．（2022秋•蜀山区校级月考）我们知道，若有理数x1，x2表示在数轴上得到点A1，A2，且x1＜x2，则点A1与点A2之间的距离为|x2﹣x1|＝x2﹣x1，现已知数轴上三点A、B、C，其中A表示的数为﹣3，B表示的数为3，C与A的距离等于m，C与B的距离等于n．请解答下列问题：（1）若点C在数轴上表示的数为﹣5，求m+n的值；（2）若m+n＝7，请你直接写出点C表示的数为；（3）若C在点A、B之间（不与点A、B重合），且m＝n，求点C表示的数．四．相反数（共1小题）12．（2022秋•鸠江区校级月考）下列各组数中，互为相反数的是（）A．﹣2022与+（﹣2022）B．﹣（﹣2022）与2022C．﹣（+2022）与+（﹣2022）D．﹣2022 与﹣（﹣2022）五．倒数（共1小题）13．（2022秋•定远县校级月考）﹣2.5的倒数是（）A．﹣2.5B．2.5C．D．﹣六．有理数大小比较（共5小题）14．（2022秋•蒙城县期中）用“＞”或“＜”填空：﹣．15．（2022秋•霍邱县期中）比较两数大小：﹣﹣（用“＜”或“＝”或“＞”填空）．16．（2022秋•亳州期末）在﹣1，1.2，﹣2，0四个数中，最小的数是（）A．﹣1B．1.2C．﹣2D．017．（2022秋•淮北月考）在下列四个数中，比﹣2023小的数是（）A．﹣2024B．﹣2022C．﹣2022.5D．018．（2022秋•无为市月考）有理数a、b在数轴上的对应点的位置如图所示．（1）比大小：|c||b|，﹣a b；（填“＞”，“＝”或“＜”）（2）化简：|2b|+|b﹣c|﹣|c﹣a|．七．有理数的减法（共2小题）19．（2021秋•长丰县期末）已知|a|＝5，b＝3，且a+b＜0，则a﹣b的值为（）A．﹣8B．﹣2C．2或﹣8D．220．（2022秋•淮北月考）阅读理解：数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如图，线段AB＝1＝0﹣（﹣1）；线段BC＝2＝2﹣0；线段AC＝3＝2﹣（﹣1）问题（1）数轴上点M、N代表的数分别为﹣9和1，则线段MN＝；（2）数轴上点E、F代表的数分别为﹣6和﹣3，则线段EF＝；（3）数轴上的两个点之间的距离为5，其中一个点表示的数为2，则另一个点表示的数为m，求m．八．非负数的性质：偶次方（共1小题）21．（2021秋•霍邱县期中）如果|a+2|+（b﹣1）2＝0，那么代数式（a+b）2021的值是（）A．1B．﹣1C．±1D．2021九．有理数的混合运算（共7小题）22．（2022秋•南陵县期中）在数学课上，老师让甲、乙、丙、丁，四位同学分别做了一道有理数运算题，你认为做对的同学是（）甲：9﹣32÷8＝0÷8＝0．乙：24﹣（4×32）＝24﹣4×6＝0．丙：（36﹣12）÷＝36×﹣12×＝16．丁：（﹣3）2÷×3＝9÷1＝9．A．甲B．乙C．丙D．丁23．（2022秋•芜湖期中）a，b互为相反数，且都不为0，c，d互为倒数，|m﹣1|＝2，则的值为．24．（2022秋•安徽期末）计算：5÷[（﹣1）3﹣4]﹣|﹣1|．25．（2022秋•蚌山区月考）计算：．26．（2022秋•颍州区校级期末）（1）计算：（）×30；（2）计算：（﹣1）4×|﹣8|+（﹣2）3×（）2．27．（2022秋•龙子湖区校级月考）已知a、b为有理数，下列说法：①若a、b互为相反数，则＝﹣1；②若|a﹣b|+a﹣b＝0，则b＞a；③若a+b＜0，ab＞0，则|3a+4b|＝﹣3a﹣4b；④若|a|＞|b|，则（a+b）•（a﹣b）是正数，其中正确的序号是．28．（2022秋•庐江县期中）小明定义了一种新的运算，取名为⊗运算，按这种运算进行运算的算式举例如下：①（+4）⊗（+2）＝+6；②（﹣4）⊗（﹣3）＝+7；③（﹣5）⊗（+3）＝﹣8；④（+6）⊗（﹣4）＝﹣10；⑤（+8）⊗0＝8；⑥0⊗（﹣9）＝9．问题：（1）请归纳⊗运算的运算法则：两数进行⊗运算时，；特别地，0和任何数进行⊗运算，或任何数和0进行⊗运算，．（2）计算：[（﹣2）⊗（+3）]⊗[（﹣12）⊗0]；（3）我们都知道乘法有结合律，这种运算律在有理数的⊗运算中还适用吗？请判断是否适用，并举例验证．一十．科学记数法—表示较大的数（共1小题）29．（2022秋•定远县校级月考）北京冬奥会标志性场馆国家速滑馆“冰丝带”近12000平方米的冰面采用分模块控制技术，可根据不同项目分区域、分标准制冰．将12000用科学记数法表示为（）A．0.12×105B．1.2×105C．1.2×104D．12×103一十一．科学记数法与有效数字（共1小题）30．（2021秋•安庆期末）下列关于近似数的说法中正确的是（）A．近似数2020精确到百位B．近似数5.78万精确到百分位C．近似数3.51×105精确到千位D．近似数5.1890精确到千分位。

第1章《有理数》计算题分类专项训练一．有理数的加法1．计算：++（﹣）．2．（﹣27）+（﹣14）+（+17）+（+8）．3．+++++．4．（1）（﹣52）+24+（﹣74）+12；（2）（+）+（﹣）+（+）+（﹣）．5．（1）（﹣25）+34+156+（﹣65）；（2）（﹣0.5）+2+2．二．有理数的减法6．计算：．7．计算：．8．计算：3﹣0.759．计算：1﹣（﹣0.5）﹣2．10．计算：3．三．有理数的乘法11．阅读理解：李华是一个勤奋好学的学生，他常常通过书籍、网络等渠道主动学习各种知识．下面是他从网络搜到的两位数乘11的速算法，其口诀是：“头尾一拉，中间相加，满十进一”例如：①24×11＝264．计算过程：24两数拉开，中间相加，即2+4＝6，最后结果264；②68×11＝748．计算过程：68两数分开，中间相加，即6+8＝14，满十进一，最后结果748．（1）计算：①32×11＝，②78×11＝；（2）若某个两位数十位数字是a，个位数字是b（a+b＜10），将这个两位数乘11，得到一个三位数，则根据上述的方法可得，该三位数百位数字是，十位数字是，个位数字是；（用含a、b的代数式表示）（3）请你结合（2）利用所学的知识解释其中原理．12．用短除法求（1）18和24的最大公因数．（2）30和45的最小公倍数．13．有6张不同数字的卡片：﹣3，+2，0，﹣8，5，+1．（1）若从中任抽两张，使得两数的积最小，求出最小的积；（2）若从中任抽三张，使得三数的积最大，求出最大的积．14．阅读理解题仔细观察下列式子，然后计算：2×3＝6，2×（﹣3）＝﹣6﹣2×3＝﹣6﹣2×（﹣3）＝6根据你得到的规律，计算：（1）﹣5×（﹣2）（2）×（﹣20）15．﹣9×15四．有理数的除法16．（1）4×；（2）7÷3．17．计算：÷（×2）．18．计算：（1）（﹣2）×3；（2）．19．小明有5张写着不同数字的卡片，请你按要求抽出卡片，完成下列各问题．（1）从中取出2张卡片，使这两张卡片上数字的乘积最大，乘积的最大值为．（2）从中取出2张卡片，使这两张卡片上数字相除的商最小，商的最小值为20．在括号内填上适当的数：．五．有理数的乘方21．计算（1）﹣32+（﹣）2×（﹣3）3÷（﹣1）25；（2）1×﹣（﹣）×2+（﹣）×．22．计算：﹣（﹣1）2+（6﹣）×+4÷（﹣）．23．计算：（﹣12.5）×（﹣8）﹣（1+﹣）×（﹣21）．24．计算下列各题：（1）13﹣（﹣）+7﹣|﹣|；（2）﹣14+9×（﹣）2+23．25．计算：4.2×[（﹣）﹣（﹣）]+（﹣0.25）．26．计算：﹣32÷（﹣1）2+|﹣3+2|．六．有理数的混合运算27．计算：（1）（﹣20）+（+3）﹣（﹣5）﹣（+7）．（2）（﹣+）÷﹣（﹣1）2021．28．计算：（1）（）×（﹣24）．（2）﹣12018+4﹣（﹣2）3+3÷（﹣）．。

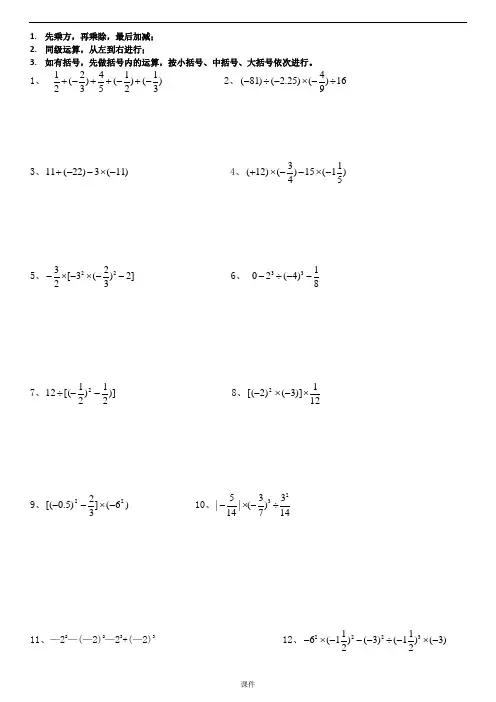
1. 先乘方，再乘除，最后加减；2. 同级运算，从左到右进行；3. 如有括号，先做括号内的运算，按小括号、中括号、大括号依次进行。

1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷3、11(22)3(11)+--⨯-4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、 33102(4)8-÷--7、)]21)21[(122--÷ 8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯-- 10、23533||()14714-⨯-÷223 3 22231113、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、－10 + 8÷(－2 )2 －(－4 )×(－3 ) 16、－49 + 2×(－3 )2 + (－6 )÷(－91)17、－14 + ( 1－0.5 )×31×[2×(－3)2] 18、(－2)2－2×[(－21)2－3×43]÷51．19、)8()4()6(52-÷---⨯ 20、0)132()43(2⨯+-+-35722523、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6－（－12）÷2)2(- 26、（-48）÷ 8 －（-5）÷2)21(-27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯- 30、(－5)×6＋(－125) ÷(－5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算：（1）618－÷）（－）（－312⨯； （2））（－＋51232⨯；（3））（－）（－49⨯＋）（－60÷12； （4）23）（－×[ ）＋（－－9532 ].（1））（－）＋（－2382⨯； （2）100÷22）（－－）（－2÷）（－32；（3））（－4÷）（－）（－343⨯； （4））（－31÷231）（－－3214）（－⨯.（1）36×23121）－（； （2）12.7÷）（－1980⨯；（3）6342＋）（－⨯； （4））（－43×）－＋（－31328；（5）1323－）（－÷）（－21； （6）320－÷34）（－81－；（7）236.15.02）－（－）（－⨯÷22）（－； （8））（－23×[ 2322－）（－ ]；（9）[ 2253）－（－）（－ ]÷）（－2； （10）16÷）（－）－（－）（－48123⨯.（1）11＋（－22）－3×（－11）； （2）0313243⨯⨯）－（－）（－；（3）2332－）（－； （4）23÷[ ）－（－）（－423]；（5））－（8743÷）（－87； （6））＋（）（－654360⨯；（7）－27+2×()23-+（－6）÷()231-； （8））（－）－＋－（－4151275420361⨯⨯.（1））－（－258÷）（－5； （2）－33121）（－－⨯；（3）223232）－（－）（－⨯⨯； （4）0132432⨯⨯）＋（－）（－；（5））（－＋51262⨯； （6）－10＋8÷()22-－4×3；（7）－51－()()[]55.24.0-⨯-； （8）()251-－（1－0.5）×31；（1）（－8）×5－40； （2）（-1.2）÷（-13）-（-2）；（3）-20÷5×14+5×（-3）÷15； （4）-3[-5+（1-0.2÷35）÷（-2）]；（5）－23÷153×（-131）2÷（132）2； （6）－52＋(1276185+-)×(－2.4)参考答案1、-1/52、-13、224、95、96、 07、-488、-19、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-20 16、23 17、2 18、24 19、-28 20、9/16 21、1 22、10 23、-1/12 24、104/3 25、9 26、14 27、-31 28、-81又1/81 29、-9 30、-29 31、-1/5 32、91、【答案】 （1）17； （2）511； （3）31； （4）－112、【答案】 （1）－10； （2）22； （3）－16； （4）－253、【答案】 （1）1； （2）0； （3）42； （4）423； （5）18； （6）0； （7）－4.64；（8）37； （9）8； （10）－25.4、【答案】 （1）22； （2）0； （3）－17； （4）－423； （5）71； （6）－95； （7）－85；（8）6 .5、【答案】 （1）3； （2）1； （3）－54； （4）0； （5）526； （6）－20； （7）－2； （8）－67. 6、【答案】（1）－80； （2）5.6； （3）－2； （4）16； （5）－516； （6）－2.9复习 有理数的乘除、乘方运算测试题一、填空题（每小题3分，共30分） 1．3×（－2）=________，（－6）×（－31）=________． 2．（－3）2的底数是________，结果是________；－32的底数是________，结果是________．3．（－61）÷（+23）=________；－493÷（－176）=________；（+8）÷（－41）=________．4．23×（－41）3=________；（－91）÷（+34）2=________．5．（－32）×________=1；（－32）×________=－16．－65×（－2．4）×（－53）=________．7．－32×（－5）2÷（－21）3=________．8．我国台湾省的面积约为3600平方公里，用科学记数法表示为________． 9．+121的倒数是________；________的倒数是－54． 10．用“＞”“＜”填空： ①23________22②（21）2________（21）3③32________22④（－2）3________（－2）2二、判断题（每小题1分，共5分） 11．零除以任何数都得零（ ）12．互为相反数的两个数的积为负数（ ） 13．如果ab ＞0，则a ＞0且b ＞0（ ）14．1除以一个非零数的商叫做这个数的倒数（ ）15．（－3）5表示5个－3相乘（ ）三、选择题（每小题3分，共21分） 16．下列说法，其中错误的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘，符号不变．A ．1个B ．2个C ．3个D ．4个17．下列各对数：①1与1；②－1与1；③a －b 与b －a ；④－1与－1；⑤－5与|6|，其中互为倒数的是A ．①②③B ．①③⑤C ．①③④D ．①④ 18．下列各题中两个式子的值相等的是A ．－23与（－2）3B ．32与23C ．（－2）2与 －22D ．|－2|与－|－2| 19．下列结论中，其中正确的个数为①0的倒数是0；②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数等于自身的数是±1；④若a ，b 互为倒数，则－ab=－1．A ．4B ．3C ．2D ．1 20．下列各式中结果大于0的是A ．1－910×3B ．（1－910）×3C ．1－（9×3）10D ．（1－9）10×3 21．下列说法中正确的是 A ．一个数的平方必为正数B ．一个数的平方必小于这个数的绝对值C ．一个数的平方必大于这个数D ．一个数的平方不可能为负数22．用科学记数法表示的数2．89×104，原来是A ．2890B ．2890000C ．28900D ．289000四、计算题（共35分）23．（3分）（－3）×（－5）×（+12）×（－21） 24．（3分）－6÷（+3）÷（－4）×（+2） 25．（3分）－5－6÷（－3）26．（3分）（－81）÷241×91÷（－16）27．（3分）－22×（－3）÷5428．（3分）（－1）2000×（－1）2001×（－1）2002÷（－1）200329．（3分）（－2）×（－2001）×［－21－（－21）］×1－200230．（3分）－)45()45(5222-÷-⨯⨯31．（3分）（－5）2÷5×632．（3分）（－2.5）÷（－310）×（－3）33．（5分）30×（21－31+53－109）五、解答题（9分）34．已知A=a+a 2+a 3+……+a 2000（1）若a =1，求A 的值．（2）若a =－1，求A 的值．参考答案一、1．－6 2 2．－3 9 3 －9 3．－91 913 －32 4．－81 －161 5．－23 23 6．－1.2 7．1800 8．3.6×103平方公里 9．32 －141 10．＞ ＞ ＞ ＜ 二、11．× 12．× 13．× 14．√ 15．√三、16．A 17．D 18．A 19．B 20．D 21．D 22．C四、23．－90 24．1 25．－3 26．41 27．15 28．1 29．－2002 30．1 31．30 32．－49 33．－4 五、34．（1）2000 （2）0。

专题训练（二） 有理数的运算类型一 加减混合运算的技巧（一） 相反数相结合或同号结合1．计算：（1）25.3+（﹣7.3）+（+13.7）+7.3 ）（）（））（（8-8032-60110-2++++（二） 同分母相加或凑整相加2. 计算（1）56.8-88.3-56.1012.7-）（）（++（2））（）（）（）（1273-1-5341251-872-522+++++（三） 裂项法3．计算：++++…+．类型二 运用分配率解题的技巧（一） 正用分配率4.计算）（）（14183-7456-+×（二） 逆用分配率5.计算：）（）（）（）（）（763-12763-7-763-5-×+×+×（三） 正用与逆用分配率6.计算：）（31121-18136-121375.41275.3-+×÷+×（四） 除法变乘法，再利用分配率7.计算：）（）（481-2413-4367-1211÷+类型三 有规律的运算与新定义运算8．符号“f ”与“g ”表示两种运算，它对一些数的运算结果如下：（1）f （1）＝0，f （2）＝1，f （3）＝2，f （4）＝3，…（2）g （）＝2，g （）＝3，g （）＝4，g （）＝5，… 利用以上规律计算：g （20201）﹣f （2020）＝ ．9．符号“f”与“g”表示两种运算，它对一些数的运算结果如下：（1）f（1）＝0，f（2）＝1，f（3）＝2，f（4）＝3，…（2）g（）＝2，g（）＝3，g（）＝4，g（）＝5，…利用以上规律计算：g（）﹣f（2018）＝．。

1.先乘方,再乘除,最后加减；之樊仲川亿创作3. 同级运算,从左到右进行；4.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.1、12411 ()()()23523+-++-+-2、4(81)( 2.25)()169-÷-⨯-÷ 3、11(22)3(11)+--⨯- 4、31(12)()15(1)45+⨯--⨯-5、2232[3()2]23-⨯-⨯--6、33102(4)8-÷--7、)]21)21[(122--÷8、121)]3()2[(2⨯-⨯-9、)6(]32)5.0[(22-⨯--10、23533||()14714-⨯-÷11、—22—(—2)2—23+(—2)3 12、2223116(1)(3)(1)(3)22-⨯---÷-⨯-13、199711(1)(10.5)()312----⨯÷- 14、33514(1)(8)(3)[(2)5]217---⨯+-÷-+15、－10 + 8÷(－2 )2－(－4 )×(－3 ) 16、－49 + 2×(－3 )2 + (－6 )÷(－91)17、－14 + ( 1－0.5 )×31×[2×(－3)2] 18、(－2)2－2×[(－21)2－3×43]÷51．19、)8()4()6(52-÷---⨯20、0)132()43(2⨯+-+- 21、6)12()4365127(÷-⨯+-22、22)4()5(25.0)4()85(-⨯-⨯--⨯-23、)23232(21)21(2--⨯+- 24、[][]332)2(3)5(6)7(4-÷--+÷-⨯-25、6－（－12）÷2)2(- 26、（-48）÷ 8 －（-5）÷2)21(- 27、42×)43()32(-+-÷ 0.25 28、()23)9181(-÷-29、()()333232÷---⨯-30、(－5)×6＋(－125) ÷(－5)331、)251(4)5(25.0-⨯⨯-⨯-- 32、22)3(61)2132(1-+÷-+-1、【基础题】计算：（1）618－÷）（－）（－312⨯； （2））（－＋51232⨯； （3））（－）（－49⨯＋）（－60÷12； （4）23）（－×[ ）＋（－－9532 ]. （1））（－）＋（－2382⨯； （2）100÷22）（－－）（－2÷）（－32； （3））（－4÷）（－）（－343⨯； （4））（－31÷231）（－－3214）（－⨯. （1）36×23121）－（； （2）12.7÷）（－1980⨯； （3）6342＋）（－⨯；（4））（－43×）－＋（－31328； （5）1323－）（－÷）（－21； （6）320－÷34）（－81－；（7）236.15.02）－（－）（－⨯÷22）（－； （8））（－23×[ 2322－）（－ ]； （9）[ 2253）－（－）（－ ]÷）（－2；（10）16÷）（－）－（－）（－48123⨯. （1）11＋（－22）－3×（－11）； （2）0313243⨯⨯）－（－）（－；（3）2332－）（－；（4）23÷[ ）－（－）（－423]； （5））－（8743÷）（－87； （6））＋（）（－654360⨯； （7）－27+2×()23-+（－6）÷()231-； （8））（－）－＋－（－4151275420361⨯⨯. （1））－（－258÷）（－5； （2）－33121）（－－⨯； （3）223232）－（－）（－⨯⨯；（4）0132432⨯⨯）＋（－）（－；（5））（－＋51262⨯； （6）－10＋8÷()22-－4×3； （7）－51－()()[]55.24.0-⨯-； （8）()251-－（1－0.5）×31； （1）（－8）×5－40； （2）（-1.2）÷（-13）-（-2）；（3）-20÷5×14+5×（-3）÷15； （4）-3[-5+（1-0.2÷35）÷（-2）]；（5）－23÷153×（-131）2÷（132）2； （6）－52＋(1276185+-)×(－2.4) 参考答案1、-1/52、-13、224、95、96、 07、-48 8、-1 9、-15 10、-15/34311、-24 12、-89 13、3 14、2 15、-2016、23 17、2 18、24 19、-28 20、9/1621、1 22、10 23、-1/12 24、104/3 25、926、1427、-3128、-81又1/81 29、-9 30、-29 31、-1/5 32、9 1、【答案】 （1）17； （2）511； （3）31； （4）－11 2、【答案】 （1）－10； （2）22； （3）－16； （4）－25 3、【答案】 （1）1； （2）0； （3）42； （4）423； （5）18； （6）0； （7）－4.64； （8）37； （9）8； （10）－25.4、【答案】 （1）22； （2）0； （3）－17； （4）－423； （5）71； （6）－95； （7）－85；（8）6 .5、【答案】 （1）3； （2）1； （3）－54； （4）0； （5）526； （6）－20； （7）－2； （8）－67.6、【答案】（1）－80； （2）5.6； （3）－2； （4）16； （5）－516； （6）－2.9温习 有理数的乘除、乘方运算测试题一、填空题（每小题3分,共30分） 1．3×（－2）=________,（－6）×（－31）=________． 2．（－3）2的底数是________,结果是________；－32的底数是________,结果是________．3．（－61）÷（+23）=________；－493÷（－176）=________；（+8）÷（－41）=________． 4．23×（－41）3=________；（－91）÷（+34）2=________．5．（－32）×________=1；（－32）×________=－16．－65×（－2．4）×（－53）=________．7．－32×（－5）2÷（－21）3=________．8．我国台湾省的面积约为3600平方千米,用科学记数法暗示为________． 9．+121的倒数是________；________的倒数是－54． 10．用“＞”“＜”填空： ①23________22②（21）2________（21）3 ③32________22④（－2）3________（－2）2二、判断题（每小题1分,共5分） 11．零除以任何数都得零（ ）12．互为相反数的两个数的积为正数（ ） 13．如果ab ＞0,则a ＞0且b ＞0（ ）14．1除以一个非零数的商叫做这个数的倒数（ ） 15．（－3）5暗示5个－3相乘（ ） 三、选择题（每小题3分,共21分） 16．下列说法,其中错误的有①一个数与1相乘得原数；②一个数乘以－1得原数的相反数；③0乘以任何数得0；④同号两数相乘,符号不变．A ．1个B ．2个C ．3个D ．4个17．下列各对数：①1与1；②－1与1；③a －b 与b －a ；④－1与－1；⑤－5与|6|,其中互为倒数的是A ．①②③B ．①③⑤C ．①③④D ．①④ 18．下列各题中两个式子的值相等的是A ．－23与（－2）3B ．32与23C ．（－2）2与 －22D ．|－2|与－|－2| 19．下列结论中,其中正确的个数为①0的倒数是0；②一个不等于0的数的倒数的相反数与这个数的相反数的倒数相等；③其倒数等于自身的数是±1；④若a,b 互为倒数,则－ab=－1．A ．4B ．3C ．2D ．1 20．下列各式中结果大于0的是 A ．1－910×3 B ．（1－910）×3 C ．1－（9×3）10 D ．（1－9）10×3 21．下列说法中正确的是 A ．一个数的平方必为正数B ．一个数的平方必小于这个数的绝对值C ．一个数的平方必大于这个数D ．一个数的平方不成能为正数22．用科学记数法暗示的数2．89×104,原来是 A ．2890 B ．2890000 C ．28900 D ．289000 四、计算题（共35分）23．（3分）（－3）×（－5）×（+12）×（－21） 24．（3分）－6÷（+3）÷（－4）×（+2） 25．（3分）－5－6÷（－3）26．（3分）（－81）÷241×91÷（－16） 27．（3分）－22×（－3）÷5428．（3分）（－1）2000×（－1）2001×（－1）2002÷（－1）200329．（3分）（－2）×（－2001）×［－21－（－21）］×1－2002 30．（3分）－)45()45(5222-÷-⨯⨯ 31．（3分）（－5）2÷5×632．（3分）（－2.5）÷（－310）×（－3） 33．（5分）30×（21－31+53－109）五、解答题（9分）34．已知A=a+a2+a3+……+a2000 （1）若a=1,求A 的值． （2）若a=－1,求A 的值．参考答案一、1．－6 2 2．－3 9 3 －9 3．－91913－32 4．－81 －161 5．－2323 6．－1.2 7．1800 8．3.6×103平方千米 9．32 －14110．＞ ＞ ＞ ＜二、11．× 12．× 13．× 14．√ 15．√三、16．A 17．D 18．A 19．B 20．D 21．D 22．C 四、23．－90 24．1 25．－3 26．4127．15 28．1 29．－2002 30．1 31．30 32．－4933．－4。

七年级上册计算题专项训练一、有理数的运算1. 计算：(-3)+5 (-2)解析：首先去括号，根据去括号法则，括号前是“+”号，把括号和它前面的“+”号去掉后，原括号里各项的符号都不改变；括号前是“”号，把括号和它前面的“”号去掉后，原括号里各项的符号都要改变。

所以原式变为-3 + 5+2。

然后按照从左到右的顺序进行计算，-3+5 = 2，2 + 2=4。

2. 计算：-2×(-3)÷(1)/(2)解析：先计算乘法，根据有理数乘法法则，两数相乘，同号得正，异号得负，并把绝对值相乘，所以-2×(-3)=6。

再计算除法，除以一个数等于乘以它的倒数，(1)/(2)的倒数是2，所以6÷(1)/(2)=6×2 = 12。

3. 计算：(-2)^3+(-3)×[(-4)^2 2]-(-3)^2解析：先计算幂运算，(-2)^3=-8，(-4)^2 = 16，(-3)^2=9。

原式变为-8+(-3)×(16 2)-9。

接着计算括号内的式子，16-2 = 14。

然后计算乘法，-3×14=-42。

最后计算加减法，-8+(-42)-9=-8 42-9=-59。

二、整式的加减1. 化简：3a + 2b 5a b解析：合并同类项，同类项是指所含字母相同，并且相同字母的指数也相同的项。

对于a的同类项，3a-5a=-2a；对于b的同类项，2b b=b。

所以化简结果为-2a + b。

2. 先化简，再求值：(2x^2 3xy + 4y^2)-3(x^2 xy+(5)/(3)y^2)，其中x = -2,y = 1解析：先去括号，2x^2-3xy + 4y^2-3x^2+3xy 5y^2。

然后合并同类项，(2x^2-3x^2)+(-3xy + 3xy)+(4y^2 5y^2)=-x^2 y^2。

当x = -2,y = 1时，代入-x^2 y^2，-(-2)^2-1^2=-4 1=-5。

专项练习有理数的混合运算技巧► 技巧一 凑零相加法1．计算：(－15.43)＋(－4.15)＋(＋15.20)＋(＋4.15)＋(＋0.23)＋(－5)． 2．计算：10－213－6－4＋23＋123＋1.3．计算：8＋5＋(－4)－(－6)＋4－(－2)＋3＋(－3)＋(－2)－9＋1. ► 技巧二 凑整相加法4．计算：(＋6.4)＋(－5.1)－(－3.9)＋(－2.4)－(＋4.9)． 5．计算：⎝ ⎛⎭⎪⎫＋235＋(－0.8)＋⎝ ⎛⎭⎪⎫＋318＋(＋2.8)＋⎝ ⎛⎭⎪⎫－18. ► 技巧三 同号相加法6．计算：(＋5)＋(－6)＋(＋4)＋(＋9)＋(－7)＋(－8)． 7．计算：－(＋0.5)－⎝ ⎛⎭⎪⎫－314＋2.75－⎝ ⎛⎭⎪⎫＋712. ► 技巧四 同分母相加 8．计算：－112＋114－⎝ ⎛⎭⎪⎫－34－⎝ ⎛⎭⎪⎫＋212. 9．计算：－1423＋11215－⎝ ⎛⎭⎪⎫－1223－14＋⎝ ⎛⎭⎪⎫－11215. ► 技巧五 巧分离相加法 10．计算：⎝ ⎛⎭⎪⎫－200056＋⎝ ⎛⎭⎪⎫－199923＋400034＋⎝ ⎛⎭⎪⎫－112. ► 技巧六 拆项相消法11．请观察以下算式： 11×2＝1－12，12×3＝12－13，13×4＝13－14，14×5＝14－15，…. (1)第10个算式为____________＝__________，第n 个算式为____________＝____________； (2)运用以上规律计算：12＋16＋112＋…＋190＋1110＋1132.► 技巧七 错位相减法12．计算：1－12＋14－18＋116－132＋164－1128.► 技巧八 逆用分配律法13．计算：25×(－18)＋(－25)×12＋25×(－10)． 14．计算：－7778÷(－7)－3338÷3.详解详析1．解：原式＝[(－15.43)＋(＋15.20)＋(＋0.23)]＋[(－4.15)＋(＋4.15)]＋(－5)＝0＋0＋(－5)＝－5. 2．解：原式＝(10－6－4)＋⎝ ⎛⎭⎪⎫－213＋23＋123＋1＝0＋0＋1＝1. 3．解：原式＝8＋5－4＋6＋4＋2＋3－3－2－9＋1＝(－4＋4)＋(2－2)＋(3－3)＋(8－9＋1)＋5＋6＝0＋0＋0＋0＋11＝11.4．解：原式＝(＋6.4)＋(－5.1)＋(＋3.9)＋(－2.4)＋(－4.9)＝6.4－5.1＋3.9－2.4－4.9＝(6.4－2.4)＋(－5.1－4.9)＋3.9＝4－10＋3.9＝－2.1. 5．解：原式＝[(－0.8)＋(＋2.8)]＋⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫＋318＋⎝ ⎛⎭⎪⎫－18＋⎝ ⎛⎭⎪⎫＋235 ＝2＋3＋235 ＝735.6．解：原式＝[(＋5)＋(＋4)＋(＋9)]＋[(－6)＋(－7)＋(－8)]＝(＋18)＋(－21)＝－3.7．解：原式＝－0.5＋314＋2.75－712 ＝⎝ ⎛⎭⎪⎫－0.5－712＋⎝ ⎛⎭⎪⎫314＋2.75 ＝－8＋6＝－2.8．解：原式＝－32＋54＋34－52＝⎝ ⎛⎭⎪⎫－32－52＋⎝ ⎛⎭⎪⎫54＋34 ＝－4＋2＝－2.9．解：原式＝－1423＋11215＋1223－14－11215＝⎝ ⎛⎭⎪⎫－1423＋1223＋⎝ ⎛⎭⎪⎫11215－11215－14 ＝－2＋0－14＝－16. 10．解：原式＝－201956－201923＋400034－112＝(－2019－2019＋4000－1)＋(－56－23＋34－12)＝0－54 ＝－54. 11．解：(1)110×11 110－111 1n 〔n ＋1〕 1n －1n ＋1 (2)12＋16＋112＋…＋190＋1110＋1132＝1－12＋12－13＋13－14＋…＋19－110＋110－111＋111－112＝1＋(－12＋12)＋(－13＋13)＋(－14＋14)＋…＋(－111＋111)－112＝1－112＝1112. 12．解：设S ＝1－12＋14－18＋116－132＋164－1128，①那么2S ＝2－1＋12－14＋18－116＋132－164.②把①和②式的左右两边分别相加， 得S ＋2S ＝2＋(1－1)＋⎝ ⎛⎭⎪⎫－12＋12＋…＋⎝⎛⎭⎪⎫164－164－1128， 那么3S ＝2－1128＝255128，所以S ＝85128，即1－12＋14－18＋116－132＋164－1128＝85128.13．解：原式＝25×(－18)－25×12＋25×(－10)＝25×(－18－12－10)＝－1000. 14．解：原式＝－(77＋78)×(－17)－(33＋38)×13＝11＋18－11－18＝0.。

专题2.4 有理数的混合运算专项训练（100题）参考答案与试题解析一．解答题（共25小题，满分100分，每小题4分）1．（4分）（2022•黄冈开学）计算：（1）(−514)+(−3.5)； （2）23+(−15)+(−1)+13；（3）−22÷(−12)−(138+213−334)×48； （4）（﹣2）2×3+（﹣3）3÷9．【分析】（1）先通分，然后根据有理数的加法法则计算即可；（2）根据加法的交换律和结合律解答即可；（3）先算乘方，然后算乘除法，最后算加减法即可；（4）先算乘方，再算乘除法，最后算加法即可．【解答】解：（1）(−514)+(−3.5)＝（﹣514）+（﹣324） ＝﹣834； （2）23+(−15)+(−1)+13＝（23+13）+[（−15）+（﹣1）] ＝1+（﹣115）=−15；（3）−22÷(−12)−(138+213−334)×48 ＝﹣4×（﹣2）−118×48−73×48+154×48＝8﹣66﹣112+180＝10；（4）（﹣2）2×3+（﹣3）3÷9＝4×3+（﹣27）÷9＝12+（﹣3）＝9．2．（4分）（2022•垦利区期末）计算：（1）（﹣5）+（﹣4）﹣（+101）﹣（﹣9）；（2）−12021×[4−(−3)2]+3÷(−34)；（3）(512−79+23)÷136；（4）−316×7−316×(−9)+(−196)×(−8)．【分析】（1）先把减法转化为加法，然后根据有理数的加法法则计算即可；（2）先算乘方和括号内的式子，然后计算括号外的乘除法、最后算加法即可；（3）先把除法转化为乘法、然后根据乘法分配律计算即可；（4）先将带分数化为假分数，然后根据乘法分配律计算即可．【解答】解：（1）（﹣5）+（﹣4）﹣（+101）﹣（﹣9）＝（﹣5）+（﹣4）+（﹣101）+9＝﹣101；（2）−12021×[4−(−3)2]+3÷(−34)＝﹣1×（4﹣9）+3×（−43）＝﹣1×（﹣5）+（﹣4）＝5+（﹣4）＝1；（3）(512−79+23)÷136＝（512−79+23）×36=512×36−79×36+23×36＝15﹣28+24＝11；（4）−316×7−316×(−9)+(−196)×(−8)=−196×7−196×（﹣9）−196×（﹣8）=−196×[7+（﹣9）+（﹣8）]=−196×（﹣10）=953．3．（4分）（2022•呼和浩特期末）计算：（1）（﹣8）×（﹣7）÷（−12）；（2）(23−34+16)÷(−124)；（3）﹣14﹣（1﹣）×13−|1﹣（﹣5）2|；（4）|13−12|÷(−112)−18×(−2)3．【分析】（1）先把除法统一成乘法，按乘法法则计算即可；（2）利用乘法的分配律计算比较简便；（3）先算乘方，再算绝对值和括号里面的，最后算乘法和加减；（4）先算乘方和绝对值里面的，再算乘除，最后算加减．【解答】解：（1）（﹣8）×（﹣7）÷（−12）＝﹣8×7×2＝﹣112；（2）(23−34+16)÷(−124)＝（23−34+16）×（﹣24）=23×（﹣24）−34×（﹣24）+16×（﹣24）＝﹣16+18﹣4＝﹣2；（3）﹣14﹣（1﹣）×13−|1﹣（﹣5）2|＝﹣1−12×13−|1﹣25|＝﹣1−16−24＝﹣2516；（4）|13−12|÷(−112)−18×(−2)3 ＝|−16|×（﹣12）−18×（﹣8）=16×（﹣12）+1＝﹣2+1＝﹣1．4．（4分）（2022•重庆期末）计算：（1）3+（﹣6）﹣（﹣7）；（2）（﹣22）×（﹣114）÷13；（3）（34−13−56）×（﹣12）； （4）﹣12023﹣（−13）×（﹣22+3）+12×|3﹣1|．【分析】（1）先把减法转化为加法，然后根据有理数加法法则计算即可；（2）先算乘方、再算乘除法即可；（3）根据乘法分配律可以解答本题；（4）先算乘方和括号内的式子，再算括号外的乘法和加减法即可．【解答】解：（1）3+（﹣6）﹣（﹣7）＝3+（﹣6）+7＝4；（2）（﹣22）×（﹣114）÷13 ＝（﹣4）×（−54）×3＝15；（3）（34−13−56）×（﹣12）=34×（﹣12）−13×（﹣12）−56×（﹣12）＝（﹣9）+4+10＝5；（4）﹣12023﹣（−13）×（﹣22+3）+12×|3﹣1|＝﹣1﹣（−13）×（﹣4+3）+12×2 ＝﹣1+13×（﹣1）+1＝﹣1+（−13）+1=−13．5．（4分）（2022•镇平县校级期末）计算：（1）|﹣2|÷（−12）+（﹣5）×（﹣2）； （2）（23−12+56）×（﹣24）； （3）15÷（−32+56）；（4）（﹣2）2﹣|﹣7|﹣3÷（−14）+（﹣3）3×（−13）2．【分析】（1）首先计算绝对值，然后计算除法、乘法，最后计算加法即可．（2）根据乘法分配律计算即可．（3）首先计算小括号里面的加法，然后计算小括号外面的除法即可．（4）首先计算乘方、绝对值，然后计算除法、乘法，最后从左向右依次计算即可．【解答】解：（1）|﹣2|÷（−12）+（﹣5）×（﹣2）＝2×（﹣2）+10＝﹣4+10＝6．（2）（23−12+56）×（﹣24）=23×（﹣24）−12×（﹣24）+56×（﹣24）＝﹣16+12﹣20＝﹣24．（3）15÷（−32+56）＝15÷（−23）＝15×（−32）＝﹣．（4）（﹣2）2﹣|﹣7|﹣3÷（−14）+（﹣3）3×（−13）2 ＝4﹣7﹣3×（﹣4）+（﹣27）×19＝4﹣7+12+（﹣3）＝﹣3+12+（﹣3）＝9+（﹣3）＝6．6．（4分）（2022•高青县期末）计算：（1）（14+38−712）÷124； （2）﹣23÷8−14×（﹣2）2；（3）﹣24+（3﹣7）2﹣2×（﹣1）2；（4）[（﹣2）3+43]÷4+（−23）． 【分析】（1）运用乘法对加法的分配律，简化计算．（2）先算乘方，再算乘除，最后算加减．（3）先算乘方，再算乘除，最后算加减．（4）先算乘方，再算中括号里的，再算除法，再算加法．【解答】解：（1）原式=(14+38−712)×24=14×24+38×24−712×24＝6+9﹣14＝1．（2）原式=−8÷8−14×4 ＝﹣1﹣1＝﹣2．（3）原式＝﹣16+（﹣4）2﹣2×1＝﹣16+16﹣2＝﹣2．（4）原式=(−8+43)÷4+(−23) =−203÷4+(−23) =−53+(−23)=−73．7．（4分）（2022•莱西市期末）计算：（1）﹣﹣﹣；（2）（−613）+（−713）﹣5； （3）25×34−（﹣25）×12+25×；（4）5×（﹣6）﹣（﹣4）2÷（﹣8）．【分析】（1）利用有理数的加减运算的法则进行求解即可；（2）利用加减运算的法则进行求解即可；（3）先把式子进行整理，再利用乘法的分配律进行求解即可；（4）先算乘方，再算乘法与除法，最后算加法即可．【解答】解：（1）﹣﹣﹣＝﹣﹣＝﹣＝﹣12；（2）（−613）+（−713）﹣5 ＝﹣1﹣5＝﹣6；（3）25×34−（﹣25）×12+25× ＝25×0.75+25×0.5+25×＝25×（）＝25×＝；（4）5×（﹣6）﹣（﹣4）2÷（﹣8）＝5×（﹣6）﹣16÷（﹣8）＝﹣30+2＝﹣28．8．（4分）（2022•越城区校级月考）计算（1）10﹣1÷（16−13）÷112（2）﹣12﹣6×（−13）2+（﹣5）×（﹣3）（3）32÷（﹣22）×（﹣114）+（﹣5）6×（−125）3 （4）[1﹣（38+16−34）×24]÷5．【分析】（1）先算括号里面的，再算除法，最后算减法即可；（2）先算乘方，再算乘法，最后算加减即可；（3）先算乘方，再算除法和乘法，最后算加减即可；（4）先算乘法，再算加减，最后算除法即可．【解答】解： （1）原式＝10﹣1÷（−16）×12＝10+72＝82；（2）原式＝﹣1﹣6×19+15 ＝﹣1−23+15 ＝1313；（3）原式＝32÷（﹣4）×（−54）+（﹣1）＝10﹣1＝9；（4）[1﹣（38+16−34）×24]÷5．＝[1﹣（9+4﹣18）]÷5＝[1﹣（﹣5）]÷5＝6÷5＝．9．（4分）（2022•宜兴市期中）计算：（1）﹣10﹣（﹣16）+（﹣24）；（2）5÷(−35)×53； （3）﹣22×7﹣（﹣3）×6+5；（4）(113+18−2.75)×（﹣24）+（﹣1）2014+（﹣3）3． 【分析】（1）根据有理数的加减混合运算进行计算即可；（2）根据有理数的乘除法进行计算即可；（3）根据有理数的混合运算进行计算即可；（4）根据有理数的混合运算进行计算即可．【解答】解：（1）原式＝﹣10+16﹣24＝﹣18；（2）原式＝﹣5×53×53=−1259；（3）原式＝﹣4×7+18+5＝﹣28+18+5＝﹣5；（4）原式=−43×24−18×24+114×24+1﹣27 ＝﹣32﹣3+66﹣26＝5．10．（4分）（2022•镇平县月考）计算：（1）（−58）÷143×（−165）÷（−67）（2）﹣3﹣[﹣5+（1﹣×35）÷（﹣2）]（3）（413−312）×（﹣2）﹣223÷（−12） （4）[50﹣（79−1112+16）×（﹣6）2]÷（﹣7）2．【分析】（1）原式从左到右依次计算即可得到结果；（2）原式先计算乘除运算，再计算加减运算即可得到结果；（3）原式先计算乘除运算，再计算加减运算即可得到结果；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．【解答】解：（1）原式=−58×314×165×76=−12； （2）原式＝﹣3+5+（1−325）×12=−3+5+1125=21125； （3）原式=−263+7+163=323；（4）原式＝（50﹣28+33﹣6）×149=49×149=1．11．（4分）（2022•饶平县校级期中）计算：（1）2﹣5+4﹣（﹣7）+（﹣6）（2）（﹣2467）÷6 （3）（﹣18）÷214×49÷（﹣16）（4）43−{(−3)4−[(−1)÷2.5+214×(−4)]÷(24815−27815)}．【分析】（1）原式利用减法法则变形，计算即可得到结果；（2）原式变形后，利用乘法分配律计算即可得到结果；（3）原式利用除法法则变形，约分即可得到结果；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．【解答】解：（1）原式＝2﹣5+4+7﹣6＝2；（2）原式＝（﹣24−67）×16=−4−17=−417；（3）原式＝﹣18×49×49×（−116）=29；（4）原式＝64﹣81+（﹣925）÷（﹣3）＝64﹣81+4715=−131315． 12．（4分）（2022•定陶区期中）计算：（1）23﹣6×（﹣3）+2×（﹣4）；（2）（﹣134）﹣（+613）﹣+103； （3）214×（−67）÷（12−2）；（4）（﹣5）3×（−35）+32÷（﹣22）×（﹣114）．【分析】（1）根据有理数的乘法和加减法可以解答本题；（2）根据有理数的加减法可以解答本题；（3）根据有理数的乘除法和减法可以解答本题；（4）根据有理数的乘方、有理数的乘除法和加法可以解答本题．【解答】解：（1）23﹣6×（﹣3）+2×（﹣4）＝23+18+（﹣8）＝33；（2）（﹣134）﹣（+613）﹣+103＝（﹣134）+（﹣613）+（﹣214）+313 ＝[（﹣134）+（﹣214）]+[（﹣613）+313] ＝（﹣4）+（﹣3）＝﹣7；（3）214×（−67）÷（12−2） =94×（−67）÷（−32） =94×67×23=97； （4）（﹣5）3×（−35）+32÷（﹣22）×（﹣114）＝（﹣125）×（−35）+32÷（﹣4）×（−54）＝75+（﹣8）×（−54）＝75+10＝85．13．（4分）（2022•甘州区期末）计算：（1）(18−13+16)×(−24)； （2）|−2|×(−1)2023−3÷12×2；（3）−12−(1−0.5)×13×[2−(−3)]2；（4）7×(−36)×(−87)×16． 【分析】（1）原式利用乘法分配律计算即可得到结果；（2）原式先计算绝对值及乘方运算，再计算乘除运算，最后算加减运算，即可得到结果；（3）原式先计算乘方及括号中的运算，再计算乘法运算，最后算加减运算，即可得到结果；（4）原式约分即可得到结果．【解答】解：（1）原式=18×（﹣24）−13×（﹣24）+16×（﹣24）＝﹣3+8﹣4＝1；（2）原式＝2×（﹣1）﹣3×2×2＝﹣2﹣12＝﹣14；（3）原式＝﹣1−12×13×25 ＝﹣1+76 =−316； （4）原式＝48．14．（4分）（2022•江都区期中）计算（1）0﹣（+3）+（﹣5）﹣（﹣7）﹣（﹣3）（2）48×（−23）﹣（﹣48）÷（﹣8） （3）﹣12×（12−34+112）（4）﹣12﹣（1﹣）×13×[3﹣（﹣3）2]．【分析】（1）先将减法转化为加法，再利用加法法则计算；（2）先算乘除，再算加法即可；（3）利用分配律计算即可；（4）先算乘方，再算乘除，最后算加减，有括号，要先做括号内的运算．【解答】解：（1）原式＝0﹣3﹣5+7+3＝﹣8+10＝2；（2）原式＝﹣32﹣6＝﹣38；（3）原式＝﹣12×12+12×34−12×112＝﹣6+9﹣1＝﹣7+9＝2；（4）原式＝﹣1−12×13×（3﹣9） ＝﹣1−12×13×（﹣6） ＝﹣1+1＝0．15．（4分）（2022•铁力市校级期中）计算：（1）25−|−112|−(+214)+(−2.75) （2）[(−12)2+(−14)×16+42]×[(−32)−3]（3）−13−(1−0.5)×13×[2−(−3)2]（4）(−5)×313+2×313+(−6)×313．【分析】（1）先计算绝对值、将减法转化为加法，再根据法则计算可得；（2）根据有理数混合运算顺序和运算法则计算可得；（3）根据有理数混合运算顺序和运算法则计算可得；（4）逆用乘法分配律提取313，再计算括号内的，最后计算乘法即可得．【解答】解：（1）原式=25−32−94−114=−1110−5＝﹣6110；（2）原式＝（14−4+16）×（−92）=494×（−92）8（3）原式＝﹣1−12×13×（﹣7）＝﹣1+76=16；（4）原式=103×（﹣5+2﹣6） =103×（﹣9）＝﹣30．16．（4分）（2022•禄丰县校级期中）计算（1）23﹣17﹣（﹣7）+（﹣16）（2）（﹣4）+|﹣8|+（﹣3）3﹣（﹣3）（3）﹣24÷（223）2﹣312×（−14）（4）×（﹣2）3﹣[4÷（−23）2+1]+（﹣1）2022．【分析】（1）根据有理数的加法法则计算即可；（2）先计算乘方、绝对值即可；（3）先算乘方，再算乘除，最后算加减即可；（4）先算乘方，再算乘除，最后算加减即可；【解答】解：（1）23﹣17﹣（﹣7）+（﹣16）＝23﹣17+7﹣16＝﹣3（2）（﹣4）+|﹣8|+（﹣3）3﹣（﹣3）＝﹣4+8﹣27+3＝﹣20（3）﹣24÷（223）2﹣312×（−14）＝﹣24×964+72×14=−278+788=−52 （4）×（﹣2）3﹣[4÷（−23）2+1]+（﹣1）2022．＝﹣2﹣（9+1）+1＝﹣1117．（4分）（2022•高新区校级期中）计算：（1）12﹣（﹣18）+（﹣12）﹣15（2）（−13）﹣（−25）+（−23）+35（3）（14−12+16）×（﹣24）（4）﹣14+（﹣2）3×（−12）﹣（﹣32）【分析】（1）减法转化为加法，依据法则计算可得；（2）减法转化为加法，运用加法的交换律和运算法则计算可得；（3）运用乘法分配律计算可得；（4）根据有理数混合运算顺序和运算法则计算可得．【解答】解：（1）原式＝12+18﹣12﹣15＝30﹣27＝3；（2）原式=−13−23+25+35=−1+1＝0；（3）原式=14×（﹣24）−12×（﹣24）+16×（﹣24）＝﹣6+12﹣4＝2；（4）原式＝﹣1+8×12+9＝﹣1+4+9＝12．18．（4分）（2022•如皋市校级月考）计算：（1）11+（﹣22）﹣3×（﹣11）（2）(−36911)÷9（3）3.52×(−47)+2.48×(−47)−13×(−47) （4）(13−12)×(−6)+(−14)÷(−18)．【分析】（1）先计算乘法，再计算加减可得；（2）将除法转化为乘法，再计算乘法可得；（3）逆用乘法分配律提取公因数−47，再计算括号内的，最后计算乘法即可得；（4）先计算乘法、除法，然后计算加减可得．【解答】解：（1）原式＝11﹣22+33＝22；（2）原式＝﹣（36+911）×19=−4−111=−4111；（3）原式＝（−47）×（﹣13）＝（−47）×（﹣7）＝4；（4）原式＝﹣2+3+2＝3．19．（4分）（2022•郯城县月考）计算（1）1+（﹣2）+|﹣2﹣3|﹣5﹣（﹣9）（2）113×（13−12）×311÷54（3）（512+23−34）×（﹣12）（4）﹣3﹣[﹣5+（1﹣2×35）÷（﹣2）]．【分析】（1）原式利用减法法则变形，计算即可求出值；（2）原式先计算括号中的运算，再计算乘除运算即可求出值；（3）原式利用乘法分配律计算即可求出值；（4）原式先计算乘除运算，再计算加减运算即可求出值．【解答】解：（1）原式＝1﹣2+5﹣5+9＝8；（2）原式=113×（−16）×311×45=−215； （3）原式=512×（﹣12）+23×（﹣12）−34×（﹣12）＝﹣5﹣8+9＝﹣4；（4）原式＝﹣3+5−110=．20．（4分）（2022•南川区校级月考）计算（1）（+45）﹣91+5+（﹣9）（2）（−34）×113÷（﹣112） （3）（−74）÷78−23×(−6)（4）[1124−（38+16−34）×24]÷5．【分析】（1）根据加法交换律和结合律简便计算；（2）将除法变为乘法，再约分计算即可求解；（3）先算乘除法，再算加法即可求解；（4）先算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．注意乘法分配律的运用．【解答】解：（1）（+45）﹣91+5+（﹣9）＝（45+5）+（﹣91﹣9）＝50﹣100＝﹣50；（2）（−34）×113÷（﹣112） =34×43×23 =23；（3）（−74）÷78−23×(−6)＝﹣2+4＝2；（4）[1124−（38+16−34）×24]÷5 ＝[1124−9﹣4+18]÷5＝6124÷5＝1524． 21．（4分）（2022•凉州区校级月考）计算：（1）74÷78−23×（﹣6）（2）（−34−59+712）÷136（3）（﹣）+（﹣）﹣（﹣）﹣|﹣5.7|（4）113×（13−12）×311÷54．【分析】（1）根据有理数的乘除法和减法可以解答本题；（2）先把除法转化为乘法，再根据乘法分配律即可解答本题；（3）根据有理数的加减法可以解答本题；（4）根据有理数的乘除法和减法可以解答本题．【解答】解：（1）74÷78−23×（﹣6）=74×87+4＝2+4＝6；（2）（−34−59+712）÷136＝（−34−59+712）×36＝﹣27﹣15+21＝﹣21；（3）（﹣）+（﹣）﹣（﹣）﹣|﹣5.7|＝（﹣）+（﹣）+2.5+（﹣）＝﹣；（4）113×（13−12）×311÷54=113×(−16)×311×45=−215．22．（4分）（2022•凉州区校级月考）计算：（1）74÷78−23×（﹣6）（2）（−34−59+712）÷136（3）（﹣）+（﹣）﹣（﹣）﹣|﹣5.7|（4）113×（13−12）×311÷54．【分析】（1）根据有理数的乘除法和减法可以解答本题；（2）先把除法转化为乘法，再根据乘法分配律即可解答本题；（3）根据有理数的加减法可以解答本题；（4）根据有理数的乘除法和减法可以解答本题．【解答】解：（1）74÷78−23×（﹣6）=74×87+4＝2+4＝6；（2）（−34−59+712）÷136＝（−34−59+712）×36＝﹣27﹣15+21＝﹣21；（3）（﹣）+（﹣）﹣（﹣）﹣|﹣5.7|＝（﹣）+（﹣）+2.5+（﹣）＝﹣；（4）113×（13−12）×311÷54=113×(−16)×311×45=−215．23．（4分）（2022•兴隆台区校级月考）计算（1）（1−38+712）×（﹣24）（2）25×16+25×13−25×12（3）（﹣1）4−17×[2﹣（﹣4）2]（4）﹣32+16÷（﹣2）×12−（﹣1）2015．【分析】（1）原式利用乘法分配律计算即可得到结果；（2）原式逆用乘法分配律计算即可得到结果；（3）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．【解答】解： （1）原式＝﹣24+9﹣14＝﹣29；（2）原式＝25×（16+13−12）＝25×0＝0；（3）原式＝1−17×（﹣14）＝1+2＝3； （4）原式＝﹣9﹣4+1＝﹣12．24．（4分）（2022•苏仙区校级期中）计算（1）23+（﹣37）﹣23+7（2）﹣10+8÷（﹣2）2﹣（﹣4）×（﹣3）（3）（23−112−415）×（﹣60）．（4）﹣12022+|﹣5|×（−85）﹣（﹣4）2÷（﹣8）．【分析】（1）原式结合后，相加即可得到结果；（2）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果；（3）原式利用乘法分配律计算即可得到结果；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可得到结果．【解答】解：（1）原式＝23﹣23﹣37+7＝﹣30；（2）原式＝﹣10+2﹣12＝﹣20；（3）原式＝﹣40+5+16＝﹣19；（4）原式＝﹣1﹣8+2＝﹣7．25．（4分）（2022•立山区期中）计算题（1）﹣81÷（﹣214）×49÷（﹣16）；（2）（−124）÷（123−54+76）；（3）﹣32÷（﹣2）3×|﹣113|×6+（﹣2）4；（4）﹣（23）2×18﹣2×（−15）÷25+|﹣8|×2+179×（﹣112）2．【分析】（1）原式从左到右依次计算即可求出值；（2）原式被除式与除式调换求出值，即可求出所求；（3）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可求出值；（4）原式先计算乘方运算，再计算乘除运算，最后算加减运算即可求出值．【解答】解：（1）原式＝﹣81×49×49×116＝﹣1；（2）（123−54+76）÷（−124）＝（123−54+76）×（﹣24）=53×（﹣24）−54×（﹣24）+76×（﹣24）＝﹣40+30﹣28＝﹣38，则原式=−138；（3）原式＝﹣9÷（﹣8）×43×6+16=98×43×6+16＝9+16＝25；（4）原式=−49×18﹣2×（−15）×52+8×+169×94＝﹣8+1+2+4＝﹣1．。

有理数乘除法则专项训练含答案1.计算：(1)5×(-4)(2)(-4)×(-9)(3)(-0.6)×(-5)(4)×(-)解：(1)5×(-4)=-(5×4)=20(2)(-4)×(-9)=4×9=36(3)(-0.6)×(-5)=0.6×5=3(4)×(-)=-(×)=-指导：(1)(4)题是异号两数相乘，先确定积的符号为“-”，再把绝对值相乘;(2)(3)题是同号两数相乘，先确定积的符号为“+”，再把绝对值相乘。

2.计算：(1)(-4)×9×(-2.5)解：(1)(-4)×9×(-2.5)=(-4)×(-2.5)×9=10×9=90指导：(1)用乘法交换律和结合律。

3.-3的倒数是()A.B.C.-3D.3[来源:]解：A指导：倒数概念以及有理数除法运算是中考命题热点。

求一个数的倒数，用1除以这个数的商即是。

注意：负数的倒数是负数，0没有倒数。

4.中百超市推出如下优惠方案：(1)一次性购物不超过100元，不享受优惠;(2)一次性购物超过100元，但不超过300元一律九折;(3)一次性购物超过300元一律八折;某人两次购物分别付款80元，252元，如果他将这两次所购商品一次性购买，则应付款()。

A.288元B.332元C.288元或316元D.332元或363元解：C指导：本题渗透了分类讨论思想。

当252元的实际价值是在300元以内时的实际价值应为：252÷0.9=280元，故应付款(280+80)×0.8=288(元);当252元的实际价值是在300元以上时的实际价值应为：252÷0.8=315(元)，故应付款(315+80)×0.8=316(元)。

第1章 有理数（易错必刷30题14种题型专项训练）➢ 正数和负数 ➢ 有理数 ➢ 数轴 ➢ 相反数 ➢ 绝对值 ➢ 有理数大小比较 ➢ 有理数的减法➢ 有理数的乘法 ➢ 有理数的乘方 ➢ 非负数的性质：偶次方 ➢ 有理数的混合运算 ➢ 科学记数法—表示较大的数 ➢ 实数大小比较 ➢ 规律型：数字的变化类一．正数和负数（共4小题）1．（2022秋•霍林郭勒市校级月考）如果向东走6km ，记作+6km ，那么﹣3km 表示（ ） A ．向西走3kmB ．向北走3kmC ．向南走3kmD ．向东走3km2．（2022秋•桂林月考）如果零上2℃记作+2℃，那么零下3℃记作 ．3．（2022秋•惠济区期中）为全力迎接全国第十四届运动会，西安市将继续加快交通高质量发展，不断增强市民获得感和幸福感．某检修小组从O 地出发，在东西向的马路上检修线路，如果规定向东行驶为正，向西行驶为负，一天中七次行驶记录如下，（单位：km ） 第一次 第二次 第三次 第四次 第五次 第六次 第七次 ﹣4+7﹣9+8+6﹣5﹣1（1）求收工时距O 地多远？ （2）在第几次记录时距O 地最远？（3）若每千米耗油0.2升，问共耗油多少升？4．（2022秋•福清市校级月考）超市购进8筐白菜，以每筐25kg 为准，超过的千克数记作正数，不足的千克数记作负数，称后的记录如下：1.5，﹣3，2，﹣0.5，1，﹣2，﹣2，﹣2.5． （1）这8筐白菜总计超过或不足多少千克？（2）这8筐白菜一共多少千克？（3）超市计划这8筐白菜按每千克3元销售，为促销超市决定打九折销售，求这8筐白菜现价比原价便宜了多少钱？二．有理数（共1小题）5．（2022秋•旌阳区校级月考）请你把下列各数填入表示它所在的数集的圈里：﹣2，﹣20%，﹣0.13，，10，，21，6.2，4.7，﹣8．正整数：{ …}；负整数：{ …}；正分数：{ …}；负分数：{ …}．三．数轴（共3小题）6．（2022秋•隆昌市校级月考）数轴上点P表示的数为﹣2，与点P距离为3个单位长度的点表示的数为（）A．1B．5C．1或﹣5D．1或57．（2022秋•雁塔区校级月考）有理数a、b、c在数轴上的位置如图所示，则|a|﹣|a﹣b|+|c﹣a|+|b﹣c|的值是（）A．2c﹣3a B．a C．2c﹣a D．2c﹣2b8．（2022秋•广信区月考）数a，b，c在数轴上的位置如图所示：化简：|a+c|+|b﹣c|﹣|c﹣b|．四．相反数（共1小题）9．（2022秋•齐河县校级月考）的相反数是（）A．2B．﹣2C．D．五．绝对值（共1小题）10．（2022秋•启东市校级月考）已知|m|＝4，|n|＝6，且m+n＝|m+n|，则m﹣n的值是（）A．﹣10B．﹣2C．﹣2或﹣10D．2六．有理数大小比较（共3小题）11．（2022秋•连山区月考）在有理数0，2，﹣1，﹣2中，最小的数是（）A．0B．2C．﹣1D．﹣212．（2022秋•高明区月考）写出一个比﹣3大的负整数为．13．（2022秋•阿图什市校级月考）在数轴上把下列各数表示出来，并用小于符号从小到大排列出来﹣2，0，|﹣4|，0.5，﹣5，﹣（﹣3）．七．有理数的减法（共1小题）14．（2022秋•扬州月考）对于含绝对值的算式，在有些情况下，可以不需要计算出结果也能将绝对值符号去掉，例如：|7﹣6|＝7﹣6；|6﹣7|＝7﹣6；＝；＝．观察上述式子的特征，解答下列问题：（1）把下列各式写成去掉绝对值符号的形式（不用写出计算结果）：①|23﹣47|＝；②＝；（2）当a＞b时，|a﹣b|＝a﹣b；当a＜b时，|a﹣b|＝；（3）计算：．八．有理数的乘法（共1小题）15．（2022秋•南安市月考）如果两数之和是负数，且它们的积是负数，那么（）A．这两个数都是负数B．这两个数都是正数C．这两个数中，一个是正数，一个是负数，且负数的绝对值较大D．这两个数中，一个是正数，一个是负数，且正数的绝对值较大九．有理数的乘方（共2小题）16．（2021秋•香洲区校级月考）下列说法正确的是（）A．倒数等于它本身的数只有1B．平方等于它本身的数只有1C．立方等于它本身的数只有1D．正数的绝对值是它本身17．（2022秋•桂林月考）下列各数中，互为相反数的是（）A．|﹣1|和1B．﹣3和﹣（﹣2）C．（﹣2）2和﹣22D．﹣3和一十．非负数的性质：偶次方（共1小题）18．（2022春•南岗区校级月考）已知|a﹣2|+（b+3）2＝0，则b a＝．一十一．有理数的混合运算（共8小题）19．（2022秋•怀柔区校级月考）如果a＞0，那么下面各式计算结果最大的是（）A．B．C．D．20．（2022秋•西城区校级月考）（1）﹣5+1﹣（﹣2）；（2）（﹣）2+8×（﹣）；（3）（+﹣）÷（﹣）；（4）[﹣33×（）2﹣|﹣1|]×（﹣）．21．（2022秋•朝阳区校级月考）计算（能用简便方法的用简便方法）：（1）（﹣3）+12+（﹣17）+（+8）；（2）；（3）；（4）．22．（2022•越秀区校级开学）39×+148×+48×．23．（2022•越秀区校级开学）．24．（2022秋•宛城区校级月考）某水果店以每箱200元的价格从水果批发市场购进20箱樱桃，若以每箱净重10千克为标准，超过的千克数记为正数，不足的千克数记为负数，称重的记录如下表：与标准重量的差值（单位：千克）﹣0.5﹣0.2500.250.30.5箱数1246n2（1）求n的值及这20箱樱桃的总重量：（2）若水果店打算以每千克25元销售这批樱桃，若全部售出可获利多少元；（3）实际上该水果店第一天以（2）中的价格只销售了这批樱桃的60%，第二天因为害怕剩余樱桃腐烂，决定降价把剩余的樱桃以原零售价的70%全部售出，水果店在销售这批樱桃过程中是盈利还是亏损，盈利或亏损多少元．25．（2022秋•朝阳区校级月考）对于任意的非零有理数a，b，定义：，解决以下问题：（1）计算（﹣3）*4；（2）计算（﹣6）*2*（﹣3）；（3）请你举例验证一下交换律即a*b＝b*a在这一运算中是否成立．（举一个例子即可）．26．（2022秋•庐江县期中）小明定义了一种新的运算，取名为⊗运算，按这种运算进行运算的算式举例如下：①（+4）⊗（+2）＝+6；②（﹣4）⊗（﹣3）＝+7；③（﹣5）⊗（+3）＝﹣8；④（+6）⊗（﹣4）＝﹣10；⑤（+8）⊗0＝8；⑥0⊗（﹣9）＝9．问题：（1）请归纳⊗运算的运算法则：两数进行⊗运算时，；特别地，0和任何数进行⊗运算，或任何数和0进行⊗运算，．（2）计算：[（﹣2）⊗（+3）]⊗[（﹣12）⊗0]；（3）我们都知道乘法有结合律，这种运算律在有理数的⊗运算中还适用吗？请判断是否适用，并举例验证．一十二．科学记数法—表示较大的数（共2小题）27．（2022秋•沈丘县月考）2021年末河南省常住人口9883万人，其中城镇常住人口5579万人，乡村常住人口4304万人；常住人口城镇化率为56.45%，比上年末提高1.02个百分点，数据“9883万”用科学记数法可以表示为（）A．9.883×107B．9.883×108C．98.83×107D．98.83×10628．（2022秋•茅箭区校级月考）据国家航天局消息，航天科技集团所研制的天问一号探测器由长征五号运载火箭发射，并成功着陆于火星预选着陆区，距离地球320000000千米．其中320000000用科学记数法表示为．一十三．实数大小比较（共1小题）29．（2021秋•松山区期中）已知数a，b表示的点在数轴上的位置如图所示．（1）在数轴上表示出a，b的相反数的位置，并将这四个数从小到大排列；（2）若数b与其相反数相距16个单位长度，则b表示的数是多少？（3）在（2）的条件下，若数a与数b的相反数表示的点相距4个单位长度，则a表示的数是多少？一十四．规律型：数字的变化类（共1小题）30．（2020秋•新市区校级月考）阅读下面的解答过程．计算：．解：因为，所以原式＝＝＝＝．根据以上解题方法计算：（1）＝﹣（n为正整数）；（2）．（3）．。

北师大版七年级计算题专项训练一、有理数运算（1 10题）1. 计算：(-2)+3 (-5)解析：首先去括号，根据去括号法则，-( 5)=5，所以原式变为-2 + 3+5。

然后按照从左到右的顺序计算，-2+3 = 1，1 + 5=6。

2. 计算：(-3)×(-4)÷(-2)解析：先计算乘法，根据有理数乘法法则，两数相乘，同号得正，异号得负，所以(-3)×(-4)=12。

再计算除法，12÷(-2)= 6。

3. 计算：(-2)^3+(-3)×[(-4)^2 2]解析：先计算指数运算，(-2)^3=-8，(-4)^2 = 16。

然后计算括号内的式子，(-4)^2-2 = 16 2=14。

接着计算乘法，(-3)×14=-42。

最后计算加法，-8+(-42)=-50。

4. 计算：(1)/(2)-<=ft(-(1)/(3))+<=ft(-(1)/(4))解析：首先去括号，-<=ft(-(1)/(3))=(1)/(3)，原式变为(1)/(2)+(1)/(3)-(1)/(4)。

通分，分母的最小公倍数是12，(1)/(2)=(6)/(12)，(1)/(3)=(4)/(12)，(1)/(4)=(3)/(12)。

然后进行计算，(6)/(12)+(4)/(12)-(3)/(12)=(6 + 4-3)/(12)=(7)/(12)。

5. 计算：(-5)×<=ft((2)/(5)-(3)/(10))解析：先计算括号内的式子，(2)/(5)-(3)/(10)=(4 3)/(10)=(1)/(10)。

再计算乘法，(-5)×(1)/(10)=-(1)/(2)。

6. 计算：-1^4-(1 0.5)×(1)/(3)×[2-(-3)^2]解析：先计算指数运算，-1^4=-1，(-3)^2 = 9。

然后计算括号内的式子，1-0.5 = 0.5=(1)/(2)，2-(-3)^2=2 9=-7。

有理数的加减乘除混合运算100道以下是一篇关于有理数加减乘除混合运算的文章。

有理数的加减乘除混合运算100道在数学中，有理数是指可以表示为两个整数的比值的数字，包括整数、分数和小数。

有理数的运算是数学中的基础内容，掌握有理数的加减乘除混合运算是进行更高级别数学运算的前提。

本文将提供100道有理数的加减乘除混合运算题目，以帮助读者巩固相关知识。

1. 1/2 + 3/4 - 5/8答案：3/82. 12/5 - 3/4 × 2/3答案：33/103. -1.5 × 2/3 ÷ 0.5答案：-94. 5/6 + (-2/3) - (-2/3)答案：5/65. -4 + (-3) × 2/5答案：-22/56. 1/4 ÷ 2/3 × 1.5答案：3/8答案：8/38. -7/8 + (-1/4) + 1/2答案：-1/89. 3.5 × (-2) - 1/3 × (-4/5)答案：7/610. -2/5 ÷ (3/4 - 5/6)答案：10/911. 1/3 + (-0.25) + 0.4 - (-1/5)答案：1.8512. 3/4 - (1/2 + 1/8)答案：13/3213. -6 × (-0.25) ÷ (-1/3)答案：414. 2.5 - (-1/4) + (-3/8)答案：2.7515. (-4) ÷ (-0.25) × (1/2)答案：32答案：3/217. 5/6 × (-1/4 - 3/5)答案：-17/6018. 0.4 ÷ 0.2 + 1/5答案：7/519. (-3/4) + (-1/2) - 0.25答案：-7/420. -0.6 × 0.3 ÷ (-0.5)答案：0.3621. (-2/3) - 1/4 + 0.2 - (-1/5)答案：-13/6022. -1.25 - (1.5 - 1/3)答案：-0.416723. 1/2 + 3/4 + (-5/8)答案：7/824. 12/5 - (3/4 × 2/3)答案：3/10答案：-326. 5/6 + (-2/3) - (-2/3)答案：5/627. -4 + ((-3) × 2/5)答案：-22/528. (1/4 ÷ 2/3) × 1.5答案：3/829. 2/3 - 1.5 ÷ (-2/5)答案：8/330. -7/8 + (-1/4) + 1/2答案：-1/8⋮经过以上30道题目的训练，相信读者对有理数的加减乘除混合运算已经有了更深入的理解。

有理数的混合运算专项训练（含解析）一．有理数的加减法专项训练1．口算：（1）（﹣13）+（+19）= （2）（﹣4.7）+（﹣5.3）=（3）（﹣2009）+（+2010）= （4）（+125）+（﹣128）=（5）（+0.1）+（﹣0.01）= （6）（﹣1.375）+（﹣1.125）=（7）（﹣0.25）+（+）= （8）（﹣8）+（﹣4）=（9）=⎪⎭⎫⎝⎛-+⎪⎭⎫⎝⎛-+127411310（10）（﹣1.125）+（+）=（11）（﹣15.8）+（+3.6）= （12）（﹣5）+0=2．口算题：（1）（+6）+（﹣9）=；（2）（﹣5）+（﹣7）=；（3）=；（4）0+（﹣6）=；（5）8﹣8=；（6）（﹣4）+（﹣6）=；（7）6+（﹣6）=；（8）（﹣4）+14=；（9）（﹣3）﹣（﹣5）=；（10）0﹣（﹣）=．3．计算：（1）5+（﹣5）；（2）﹣23+（+58）﹣（﹣5）；（3）﹣4+28﹣（﹣29）+（﹣24）；（4）（﹣49）﹣（+91）﹣（﹣5）+（﹣9）；（5）﹣7.2﹣0.8﹣5.6+11.6；（6）（﹣）﹣（﹣0.2）+1；（7）|﹣3+1|﹣（﹣2）；（8）+（﹣）+（+）+（﹣）．4．计算：（1）45+（﹣20）；（2）（﹣8）﹣（﹣1）；（3）|﹣10|+|+8|；（4）（﹣12）﹣5+（﹣14）﹣（﹣39）；（5）0.47﹣4﹣（﹣1.53）﹣1；（6）36﹣76+（﹣23）﹣105；（7）﹣20+|﹣14|﹣（﹣18）﹣13；（8）（+1.75）+（﹣）+（+）+（+1.05）+（﹣）+（+2.2）．5．计算：（1）（﹣4）﹣（+11）﹣（﹣9）；（2）12﹣（﹣18）+（﹣12）﹣15；（3）（﹣83）+（+26）+（﹣41）+（+15）；（4）（﹣1.8）+（+0.7）+（﹣0.9）+1.3+（﹣0.2）；（5）|﹣|﹣（﹣2.5）+1﹣|1﹣|；（6）4+8﹣（+3）+（﹣1）+（﹣2）．6．计算（1）（﹣23）+（﹣12）（2）（﹣2）﹣（﹣5）+（﹣9）﹣（﹣7）（3）（﹣5.5）+（﹣3.2）﹣（﹣2.5）﹣4.8 （4）（﹣4）﹣（+5）﹣（﹣4）（5）﹣|﹣1|﹣（+2）﹣（﹣2.75）（6）（﹣0.5）﹣（﹣3）+3.75﹣（+8）．7．计算：（1）（﹣4）+9﹣（﹣7）﹣13 （2）（+18）+（﹣32）+（﹣16）+（+26）（3）5+（﹣5）+4+（﹣）（4）（﹣6.37）+（﹣3）+6.37+2.75（5）（﹣1）﹣（+6）﹣2.25+（6）﹣0.5+（﹣15）﹣（﹣17）﹣|﹣12|8．计算：（1）（﹣）+（+）+（+）+（﹣1）（2）（﹣3）+（+8）﹣（﹣5）（3）（﹣3）﹣（﹣）+（﹣0.5）+3（4）（+3）+（﹣2）﹣（﹣5）﹣（+）（5）（﹣0.25）+（﹣3）﹣|﹣1|﹣（﹣3）（6）（+）+（+17）+（﹣1）﹣（+7）﹣（﹣2）+（﹣）二．有理数的乘法专项训练9．计算：（1）﹣0.75×（﹣0.4 ）×1；（2）0.6×（﹣）•（﹣）•（﹣2）10．用简便方法计算：（1）﹣13×﹣0.34×+×（﹣13）﹣×0.34 （2）（﹣﹣+﹣）×（﹣60）11．简便计算（1）（﹣48）×0.125+48×（2）（）×（﹣36）12．计算：（1）；（2）．13．用简便方法计算（1）（﹣3.7）×（﹣0.125）×（﹣8）（2）（﹣﹣）×（﹣12）（3）﹣17×（﹣3）（4）﹣5×（﹣）+13×（﹣）﹣3×（﹣）14．计算下列各式：（1）（﹣4）×1.25×（﹣8）；（2）×（﹣2.4）×；（3）（﹣14）×（﹣100）×（﹣6）×（0.01）；（4）9×15；（5）﹣100×﹣0.125×35.5+14.5×（﹣12.5%）；（6）（1﹣2）×（2﹣3）×（3﹣4）×（4﹣5）×…（19﹣20）．三．有理数的除法专项训练15．计算：（1）﹣5÷（﹣1）；（2）（﹣）÷（﹣）÷（﹣1）．16．计算：（1）（﹣36）÷9 （2）（﹣）×（﹣3）÷（﹣1）÷3．17．计算（1）﹣3÷（）÷（）（2）（﹣﹣+）÷．18．计算（1）；（2）．（3）；（4）．四．有理数的乘方专项训练19．﹣10+8÷（﹣2）2﹣（﹣2）3×（﹣3）20．计算：（﹣2）3+（﹣3）×[（﹣4）2+2]﹣（﹣3）2÷（﹣2）21．计算：﹣14﹣（1﹣0.5）××[2﹣（﹣3）2]．22．计算﹣72+2×（﹣3）2+（﹣6）÷（﹣）2．五．有理数的混合运算专项训练23．计算（1）5.02﹣1.37﹣2.63 （2）72×（﹣+﹣）（3）×[÷（﹣）] （4）[﹣（﹣）÷]÷．24．（1）7+（﹣5）﹣（﹣3）+（6）（2）（﹣2）÷（2）×（﹣2.8）（3）25×+（﹣25）×+25×（﹣）（4）（﹣99）×99（5）﹣12017﹣[2﹣（1﹣×0.5）]×[32﹣（﹣2）2] （6）|﹣|+[×22﹣（﹣）2]．有理数的混合运算专项训练参考答案与试题解析一．解答题（共24小题）1．口算：解：（﹣13）+（+19）=6；（﹣4.7）+（﹣5.3）=﹣10；（﹣2009）+（+2010）=1；（+125）+（﹣128）=﹣3；（+0.1）+（﹣0.01）=0.09；（﹣1.375）+（﹣1.125）=﹣2.5；（﹣0.25）+（+）=；（﹣8）+（﹣4）=﹣12；+（﹣）+（﹣）=0；（﹣1.125）+（+）=﹣；（﹣15.8）+（+3.6）=﹣12.2；（﹣5）+0=﹣5．2．口算题：（1）（+6）+（﹣9）=﹣3；（2）（﹣5）+（﹣7）=﹣12；（3）=；（4）0+（﹣6）=﹣6；（5）8﹣8=0；（6）（﹣4）+（﹣6）=﹣10；（7）6+（﹣6）=0；（8）（﹣4）+14=10；（9）（﹣3）﹣（﹣5）=2；（10）0﹣（﹣）=．3．计算：解：（1）5+（﹣5）=0；（2）﹣23+（+58）﹣（﹣5）=﹣23+58+5=﹣23+63=40；（3）﹣4+28﹣（﹣29）+（﹣24）=﹣4+28+29﹣24=﹣28+28+29=29；（4）（﹣49）﹣（+91）﹣（﹣5）+（﹣9）=﹣49﹣91+5﹣9=﹣149+5=﹣144；（5）﹣7.2﹣0.8﹣5.6+11.6=﹣8+6=﹣2；（6）（﹣）﹣（﹣0.2）+1=﹣1+1=0；（7）|﹣3+1|﹣（﹣2）=2+2=4；（8）+（﹣）+（+）+（﹣）=（+）+（﹣﹣）=1﹣1=0．4．计算：解：（1）45+（﹣20）=25；（2）（﹣8）﹣（﹣1）=﹣8+1=﹣7；（3）|﹣10|+|+8|=10+8=18；（4）（﹣12）﹣5+（﹣14）﹣（﹣39）=﹣12﹣5﹣14+39=8；（5）0.47﹣4﹣（﹣1.53）﹣1=（0.47+1.53）﹣（4+1）=2﹣6=﹣4；（6）36﹣76+（﹣23）﹣105=36﹣（76+23+105）=36﹣204=﹣168；（7）﹣20+|﹣14|﹣（﹣18）﹣13=﹣20﹣13+14+18=﹣33+32=﹣1；（8）（+1.75）+（﹣）+（+）+（+1.05）+（﹣）+（+2.2）=（1.75+1.05）+（0.8+2.2）﹣（+）=2.8+3﹣1=4.8．5．计算：解：（1）（﹣4）﹣（+11）﹣（﹣9）=﹣4﹣11+9=﹣6；（2）12﹣（﹣18）+（﹣12）﹣15=12+18﹣12﹣15=3；（3）（﹣83）+（+26）+（﹣41）+（+15）=﹣83+26﹣41+15=﹣83；（4）（﹣1.8）+（+0.7）+（﹣0.9）+1.3+（﹣0.2）=﹣1.8+0.7﹣0.9+1.3﹣0.2=﹣0.9；（5）|﹣|﹣（﹣2.5）+1﹣|1﹣|=2+2.5+1﹣2+1=4.5；（6）4+8﹣（+3）+（﹣1）+（﹣2）=4+8﹣3﹣1﹣2=5．6．计算解：（1）（﹣23）+（﹣12）=﹣（23+12）=﹣35；（2）（﹣2）﹣（﹣5）+（﹣9）﹣（﹣7）=（﹣2）+（+5）+（﹣9）+（+7）=12﹣11=1；（3）（﹣5.5）+（﹣3.2）﹣（﹣2.5）﹣4.8 =（﹣5.5）+（﹣3.2）+（+2.5）﹣4.8=（﹣5.5+2.5）+（﹣3.2﹣4.8）=﹣3﹣8=﹣11；（4）（﹣4）﹣（+5）﹣（﹣4）=（﹣4）+（﹣5）+（+4）=﹣5（5）﹣|﹣1|﹣（+2）﹣（﹣2.75）=0.4﹣1.5﹣2.25+2.75=﹣0.6（6）（﹣0.5）﹣（﹣3）+3.75﹣（+8）=（﹣0.5）+（+3.25）+3.75﹣8.5=﹣27．计算：解：（1）（﹣4）+9﹣（﹣7）﹣13=﹣4+9+7﹣13=（9+7）+（﹣4﹣13）=16+（﹣17）=﹣1（2）（+18）+（﹣32）+（﹣16）+（+26）=18﹣32﹣16+26=（18+26）+（﹣32﹣16）=44+（﹣48）=﹣4（3）5+（﹣5）+4+（﹣）=（5+4）+[（﹣5）+（﹣）]=10+（﹣6）=4（4）（﹣6.37）+（﹣3）+6.37+2.75=[）（﹣6.37）+6.37]+[（﹣3.75）+2.75]=0+（﹣3.75）+2.75=﹣1（5）（﹣1）﹣（+6）﹣2.25+=（﹣1）+（﹣6）+（﹣2.25）+=[（﹣1）+（﹣2.25）]+[（﹣6）+]=（﹣4）+（﹣3）=﹣7（6）﹣0.5+（﹣15）﹣（﹣17）﹣|﹣12|=﹣0.5﹣15+17﹣12=（﹣0.5﹣15﹣12）+17=（﹣27.5）+17=﹣10.5 8．计算：解：（1）原式=﹣﹣1++=﹣2+1=﹣1；（2）原式=﹣3+5+8=2+8=11；（3）原式=﹣3﹣++3=﹣4+4=0；（4）原式=3+5﹣2﹣=9﹣3=6；（5）原式=﹣﹣1﹣3+3=﹣2；（6）原式=﹣+17﹣7﹣1+2=10+1=11．9．计算：解：（1）﹣0.75×（﹣0.4 ）×1==．（2）0.6×（﹣）•（﹣）•（﹣2）=﹣=﹣110．用简便方法计算：解：（1）﹣13×﹣0.34×+×（﹣13）﹣×0.34=﹣13×﹣×13﹣×0.34﹣0.34×=﹣13×（+）﹣（+）×0.34=﹣13×1﹣1×0.34=﹣13﹣0.34=﹣13.34（2）（﹣﹣+﹣）×（﹣60）=（﹣）×（﹣60）﹣×（﹣60）+×（﹣60）﹣×（﹣60）=20+15﹣12+28=5111．简便计算解：（1）（﹣48）×0.125+48×=48×（﹣+﹣）=0；（2）（）×（﹣36）=﹣20+27﹣2=5．12．计算：解：（1）原式=×12+×12﹣=﹣1；（2）原式=﹣（0.25×4×）=．13．用简便方法计算解：（1）（﹣3.7）×（﹣0.125）×（﹣8），=（﹣3.7）×1，=﹣3.7；（2）（﹣﹣）×（﹣12），=×（﹣12）﹣×（﹣12）﹣×（﹣12），=﹣4+2+1，=﹣1；（3）﹣17×（﹣3），=﹣17×（﹣4+），=﹣17×（﹣4）+（﹣17）×，=68﹣1，=67；（4）﹣5×（﹣）+13×（﹣）﹣3×（﹣），=（﹣）×（﹣5+13﹣3），=（﹣）×5，=﹣11．14．计算下列各式：解：（1）（﹣4）×1.25×（﹣8）=（﹣）××（﹣8）=××8=；（2）×（﹣2.4）×=﹣×2.4×=﹣1.2；（3）（﹣14）×（﹣100）×（﹣6）×（0.01）=（﹣100）×（0.01）×（﹣14）×（﹣6）=﹣1×84=﹣84；（4）9×15=（10﹣）×15=10×15﹣×15=150﹣=149；（5）﹣100×﹣0.125×35.5+14.5×（﹣12.5%）=﹣100×0.125﹣0.125×35.5+14.5×（﹣0.125）=0.125×（﹣100﹣35.5﹣14.5）=0.125×（﹣150）=﹣；（6）（1﹣2）×（2﹣3）×（3﹣4）×（4﹣5）×…×（19﹣20）=（﹣1）×（﹣1）×（﹣1）×（﹣1）×…×（﹣1）=﹣1．15．计算：解：（1）﹣5÷（﹣1）=5×=3．（2）（﹣）÷（﹣）÷（﹣1）=﹣=﹣．16．计算：解：（1）原式=﹣（36+）×，=﹣（36×+×），=﹣4；（2）原式=﹣（×××），=﹣．17．计算解：（1）原式=﹣3××=﹣；（2）原式=（﹣﹣+）×36=﹣27﹣20+21=﹣26．18．计算解：（1）﹣1÷（﹣）﹣3÷（﹣）=﹣1×（﹣8）﹣3×（﹣2）=8+6=14；（2）﹣81÷﹣÷（﹣）=﹣81×3﹣×（﹣9）=﹣243+3=﹣240；（3）﹣1+5÷（﹣）×（﹣6）=﹣1+5×（﹣6）×（﹣6）=﹣1+180=179；（4）（﹣）÷1÷=﹣××10=﹣．19．﹣10+8÷（﹣2）2﹣（﹣2）3×（﹣3）【解答】解：原式=﹣10+2﹣24=﹣34+2=﹣32．20．（2017•石家庄模拟）计算：（﹣2）3+（﹣3）×[（﹣4）2+2]﹣（﹣3）2÷（﹣2）【解答】解：原式=﹣8+（﹣3）×18﹣9÷（﹣2），=﹣8﹣54﹣9÷（﹣2），=﹣62+4.5，=﹣57.5．21．计算：﹣14﹣（1﹣0.5）××[2﹣（﹣3）2]．【解答】解：原式=﹣1﹣0.5××（2﹣9）=﹣1﹣（﹣）=．22．（2017•文昌校级模拟）计算﹣72+2×（﹣3）2+（﹣6）÷（﹣）2．【解答】解：原式=﹣49+2×9+（﹣6）÷=﹣49+18﹣6×9=﹣49+18﹣54=﹣85．23．计算解：（1）5.02﹣1.37﹣2.63=5.02﹣（1.37+2.63）=5.02﹣4=1.02（2）72×（﹣+﹣）=72×﹣72×+72×﹣72×=36﹣24+18﹣6=12+18﹣6=24（3）×[÷（﹣）]=×[÷]=×=4（4）[﹣（﹣）÷]÷=[﹣÷]×10=[﹣]×10=×10=124．解：（1）7+（﹣5）﹣（﹣3）+（6）=（7+3）+（﹣5+6）=11+1=12；（2）（﹣2）÷（2）×（﹣2.8）=××=；（3）25×+（﹣25）×+25×（﹣）=25×（﹣﹣）=25×0=0；（4）（﹣99）×99=（﹣100+）×99=﹣100×99+×99=﹣9900+1=﹣9899；（5）﹣12017﹣[2﹣（1﹣×0.5）]×[32﹣（﹣2）2]=﹣1﹣[2﹣（1﹣）]×[9﹣4]=﹣1﹣×5 =﹣1﹣5=﹣6；（6）|﹣|+[×22﹣（﹣）2]=+[×4﹣]=+[2﹣]=﹣=﹣．。