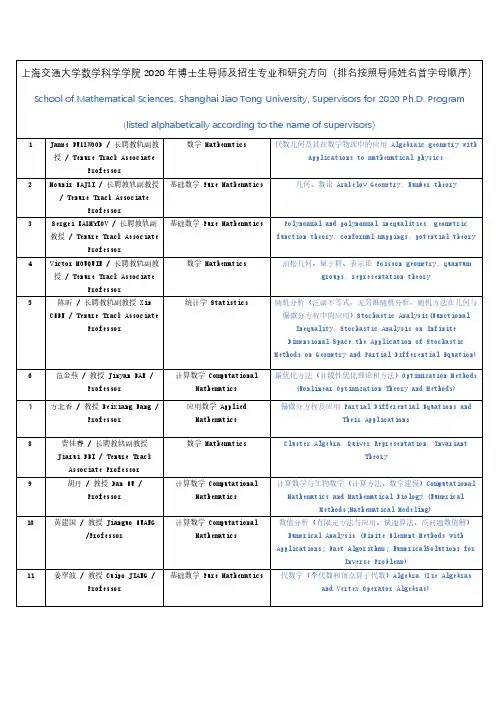
SJTU多尺度材料模拟与计算
- 格式:pdf
- 大小:386.54 KB
- 文档页数:4

2005年上海交通大学材料科学基础考博试卷[回忆版]材料科学基础:8选5。
每题两问,每问10分,我当10个题说吧,好多我也记不清是那个题下的小问了。
1。
填空。
你同学应该买那本材料科学基础习题了吧,看好那本此题就没多大问题,因为重复性很强。
2。
论述刃位错和螺位错的异同点3。
画晶面和晶向,立方密排六方一定要会,不仅是低指数;三种晶型的一些参数象原子数配位数之类的4。
计算螺位错的应力。
那本习题也有类似的,本题连续考了两年,让你同学注意下此题5。
置换固熔体、间隙固熔体的概念,并说明间隙固熔体、间隙相、间隙化合物的区别。
那本习题上有答案、6。
扩散系数定义,及对他的影响因素7。
伪共晶定义,还有个相关的什么共晶吧,区分下。
根据这概念好像有个类似计算的题,这我没做,不太记得了,总之就是共晶后面有点内容看下8。
关于固熔的题,好像是不同晶型影响固熔程度的题,我就记得当时我画了个铁碳相图举例说明了下还有两个关于高分子的题,我没做也没看是啥题总之,我觉得复习材科把握课本及习题,习题很重要,有原题,而且我发现交大考试重基础,基本概念要搞清楚,就没问题。
上海交通大学2012年材料科学基础考博试卷[回忆版]5 个大题,每个大题20分。
下面列出的是材料科学基础的前五个大题,其中第一大题有几个想不起来了,暂列9个。
其实后边还有三道大题,一道是关于高分子的,一道是关于配位多面体的,还有最后一个是作为一个材料工作者结合经验谈谈对材料科学特别是对材料强韧化的看法和建议,我都没敢选。
一填空(20分,每空1分)1 密排六方晶体有()个八面体间隙,()个四面体间隙2 晶体可能存在的空间群有(230)种,可能存在的点群有(32)种。
3 离子晶体中,正负离子间的平衡距离取决于(),而正离子的配位数则取决于()。
(鲍林第一规则)4 共价晶体的配位数服从()法则。
5 固溶体按溶解度分为有限固溶体和无限固溶体,那么()固溶体永远属于有限固溶体。
6 空位浓度的计算公式:()。

材料科学与工程的多尺度计算模拟技术材料科学与工程是一门研究材料的组成、结构、性质以及制备与应用的学科。
随着计算机技术的不断发展,多尺度计算模拟技术逐渐成为材料科学研究中不可或缺的重要工具。
多尺度模拟技术可以帮助研究人员从微观和宏观两个层面上理解材料的行为,为新材料的设计与开发提供指导和支持。
多尺度模拟技术是指将不同尺度下的模型和方法相结合,对材料进行全面深入的研究。
目前,多尺度模拟技术主要包括分子动力学模拟、量子力学模拟和连续介质模拟等方法。
这些方法可以从不同的角度描述材料的结构、力学性能、热学性能等各个方面,并对材料的行为进行预测和优化。
分子动力学模拟是一种以原子或分子为基本单元,通过数值计算模拟材料内部粒子的运动和相互作用来研究材料的方法。
它可以模拟分子尺度下材料的性质与行为,如材料的力学性能、热学性能、电学性能等。
通过分子动力学模拟,可以推导出材料的物理性质与力学性能的规律,并为新材料的设计与开发提供指导。
量子力学模拟是一种以原子核和电子的量子力学运动方程为基础,通过求解这些方程来预测材料的性质与行为的方法。
它可以模拟材料的电子结构、能带结构、光学性质等。
量子力学模拟可以提供高精度的材料性质预测,对于研究材料的电学、磁学、光学等性质具有重要意义。
连续介质模拟是一种将材料看作连续均匀介质的模拟方法。
它将材料分为小的体积元,通过数值模拟来计算和预测材料的宏观性质和行为。
连续介质模拟可以模拟材料的力学性能、热学性能、流体性质等。
它能够处理大尺度和长时间尺度的问题,对于材料的宏观行为研究具有重要意义。
多尺度模拟技术将上述不同尺度的模拟方法相结合,可以在不同层面上研究材料。
例如,分子动力学模拟可以提供原子尺度下材料的局部结构信息,而连续介质模拟则可以提供宏观尺度下材料的宏观性能信息。
通过多尺度模拟,可以将两者的结果相结合,形成全面、准确的材料性质与行为的认识。
多尺度模拟技术在材料科学与工程领域的应用非常广泛。

多尺度计算模型在材料力学中的应用研究材料力学是研究材料在外力作用下的应变和变形行为的学科。
随着科技的不断发展,对材料力学的研究也日趋深入。
尤其是近年来,多尺度计算模型在材料力学中的应用越来越受到关注。
多尺度计算模型是一种综合不同尺度的方法,用于研究材料的力学特性。
它能够从微观尺度到宏观尺度,对材料的各种物理和力学性质进行建模和计算。
这种模型的应用,可以帮助我们更好地理解材料的力学行为,并为材料设计和工程应用提供指导。
在材料力学中,多尺度计算模型主要包括两个层次:微观尺度和宏观尺度。
微观尺度主要研究材料的原子、分子结构和微观力学性质,而宏观尺度则侧重于材料的整体力学行为。
这两个层次之间存在着相互耦合的关系,多尺度计算模型正是基于这种关系来构建材料力学模型的。
在微观尺度上,多尺度计算模型可以通过原子力学模拟、分子动力学模拟等方法来研究材料的微观力学性质。
通过这些模拟方法,我们可以获得材料在不同应变率、温度等条件下的力学行为,并揭示材料的微观变形机制。
同时,这些模拟结果还可以与实验数据进行比对,从而验证模型的准确性。
在宏观尺度上,多尺度计算模型可以利用有限元法等方法对材料进行宏观力学建模。
通过建立合适的力学方程,我们可以预测材料在不同载荷条件下的应力、应变和变形行为。
此外,多尺度计算模型还可以将微观尺度的模拟结果与宏观尺度的力学模型进行耦合,从而得到更加准确的力学行为。
除了在理论研究中的应用,多尺度计算模型在材料力学中的应用还包括材料设计和工程应用。
利用这种模型,我们可以快速筛选出符合特定要求的材料,并优化材料的力学性能。
例如,通过模拟和优化材料的微观结构和组分分布,我们可以设计出更高强度、更轻量的材料。
此外,在材料工程应用中,多尺度计算模型还可以用于预测材料在不同工况下的损伤行为,为工程实践提供可靠的预测和指导。
总之,多尺度计算模型在材料力学中的应用研究是一个深入且具有广阔前景的领域。
它不仅可以为我们解析和解释材料的力学行为提供深入理论研究,还可以为材料设计和工程应用提供强有力的支持。

材料力学行为的多尺度模拟与分析材料力学行为是研究材料在外力作用下的变形、破坏和失效等现象的学科。
多尺度模拟与分析则是一种研究方法,旨在从不同尺度上理解和解释材料力学行为的本质。
本文将介绍多尺度模拟与分析在材料力学领域的应用,并探讨其意义与前景。
一、尺度效应与多尺度模拟材料存在着尺度效应,即材料在不同尺度上具有不同的力学行为。
以纳米材料为例,由于其尺寸接近原子尺度,其力学性质受到原子间作用的影响,具有明显的尺度效应。
随着材料研究的深入,人们逐渐认识到单纯从宏观尺度上研究材料的力学行为是不够全面和准确的,因此出现了多尺度模拟方法。
多尺度模拟是一种将材料力学行为从宏观到微观各个尺度上进行综合建模和仿真的方法。
其核心思想是将材料分为不同层次的子系统,通过子系统间的相互作用来模拟和分析材料的力学行为。
常见的多尺度模拟方法包括分子动力学模拟、有限元方法和连续介质力学模拟等。
二、多尺度模拟的应用多尺度模拟在材料力学领域有着广泛的应用。
首先,多尺度模拟能够帮助人们深入研究材料的本质力学行为。
通过将材料分解为不同尺度的子系统,并建立相应的物理数学模型,可以揭示材料在微观尺度上的内部机制和动力学过程。
这对于理解材料的结构、性能与行为之间的关系具有重要意义。
其次,多尺度模拟能够预测材料的宏观力学性能。
通过模拟材料在不同尺度下的行为,可以得到材料在宏观尺度上的物理性质,如强度、刚度和韧性等。
这将有助于人们设计出更高性能的材料,并指导实际工程中的材料选择和应用。
此外,多尺度模拟还可以研究材料的破坏与失效机制。
在材料受到外界载荷作用下,通过模拟和分析材料在不同尺度下的破坏模式和损伤演化过程,可以识别材料的弱点,并提出相应的改进措施,以提高材料的破坏韧性和可靠性。
三、多尺度模拟的挑战与前景多尺度模拟虽然在材料力学领域有着广泛的应用,但仍然面临着一些挑战。
首先,多尺度模拟的建模和计算过程较为复杂,需要耗费大量的时间和计算资源。


二维导热物体温度场的数值模拟一、物理问题有一个用砖砌成的长方形截面的冷空气通道,其截面尺寸如下图1-1所示,假设在垂直于纸面方向上用冷空气及砖墙的温度变化很小,可以近似地予以忽略。
在下列两种情况下试计算: 砖墙横截面上的温度分布;垂直于纸面方向的每米长度上通过砖墙的导热量。
第一种情况:内外壁分别均匀维持在0℃及30℃; 第二种情况:内外壁均为第三类边界条件,且已知:Km K m W h C t Km W h C t ∙=∙=︒=∙=︒=∞∞/35.0/93.3,10/35.10,30222211λ砖墙导热系数二、数学描写由对称的界面必是绝热面,可取左上方的四分之一墙角为研究对象,该问题为二维、稳态、无内热源的导热问题。
控制方程:02222=∂∂+∂∂y tx t边界条件: 第一种情况:由对称性知边界1绝热: 0=w q ; 边界2为等温边界,满足第一类边界条件: C t w ︒=0;1-1图2-1图边界3为等温边界,满足第一类边界条件: C t w ︒=30。
第一种情况:由对称性知边界1绝热: 0=w q ;边界2为对流边界,满足第三类边界条件: )()(2f w w w t t h n tq -=∂∂-=λ; 边界3为对流边界,满足第三类边界条件: )()(2f w w w t t h ntq -=∂∂-=λ。
三、方程离散用一系列与坐标轴平行的间隔0.1m 的二维网格线将温度区域划分为若干子区域,如图1-3所示。
采用热平衡法,利用傅里叶导热定律和能量守恒定律,按照以导入元体(m,n )方向的热流量为正,列写每个节点代表的元体的代数方程,第一种情况: 边界点:边界1(绝热边界):5~2)2(411,11,12,1,m =++=+-m t t t t m m m , 11~8)2(411,161,16,15,16=++=+-n t t t t n n n n,3-1图边界2(等温内边界): 7,16~7;7~1,6,0,=====n m n m t nm边界3(等温外边界): 12,16~2;12~1,1,30,=====n m n m t n m内节点:11~8,15~6;11~2,5~2)(411,1,,1,1,====+++=-+-+n m n m t t t t t n m n m n m n m n m第二种情况 边界点:边界1(绝热边界): 5~2)2(411,11,12,1,m =++=+-m t t t t m m m , 11~8)2(411,161,16,15,16=++=+-n t t t t n n n n ,边界2(内对流边界):6~1)2(222111,61,6,5,6=++++=∆∆-+n Bi t Bi t t t t n n n n ,16~7)2(2221117,17,18,7,=++++=∆∆-+m Bi t Bi t t t t m m m m ,边界3(外对流边界):11~1)2(2222221,11,1,2,1=++++=∆∆-+n Bi t Bi t t t t n n n n,16~2)2(22222212,112,111,12,=++++=∆∆-+m Bi t Bi t t t t m m m m ,内角点: )3(22)(21116,67,78,67,57,6+++++=∆∆Bi t Bi t t t t t外角点:)1(222211,112,212,1+++=∆∆Bi t Bi t t t内节点:11~8,15~6;11~2,5~2);(411,1,,1,1,====+++=-+-+n m n m t t t t t n m n m n m n m n m(10,22121==∆=∞∆t t xh Bi λ;30,21212==∆=∞∆t t xh Bi λ)四、编程思路及流程图编程思路为设定两个二维数组t(i,j)、ta(i,j)分别表示本次迭代和上次迭代各节点的温度值,iter (实际编程时并未按照此名称来命名迭代步长)表示迭代进行的次数, 1Q 、2Q 分别表示外边界、内边界的散热量。
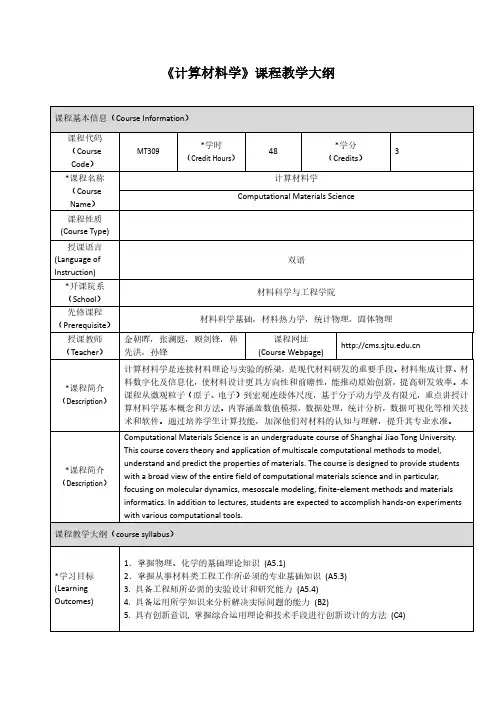

材料模拟与计算课程代码:83071000课程名称:材料模拟与计算英文名称:Materials Simulation and Calculation学分: 4 开课学期:第10学期授课对象:应用物理专业本科学生先修课程:量子力学,固体物理,热力学统计物理课程主任:吴爱玲,副教授,博士课程简介:《材料模拟与计算》课程是物理学和材料物理学等专业的专业方向课程。
该课程主要讲授材料模拟的物理化学基础——量子化学基本原理及应用,密度泛函理论方法,分子力学和分子动力学方法,以及材料模拟常见软件简介等内容。
通过本课程的学习,要求学生掌握材料设计的基本原理和计算模拟的基本方法以及常见模拟软件的使用,从而使学生从计算模拟的角度加深对材料和凝聚态物质的结构与物性的认识。
课程考核:课程最终成绩=平时成绩*30%+期末论文成绩*70%;平时成绩由出勤率、作业的完成情况决定;期末考试采取论文形式。
指定教材:无合适的教科书参考书目:[1] 《量子化学基本原理和从头计算法》(中),徐光宪,黎乐民,王德民,北京:科学出版社,2003;[2] 《现代材料计算与设计教程》,吴兴惠,项金钟,北京:电子工业出版社,2002。
[3] 《分子模拟的理论与实践》,陈正隆,徐为人, 汤立达,北京:化学工业出版社,2007。
[4] 《量子化学计算方法与应用》,林梦海,北京:科学出版社,2004。
[5] 《Molecular Modeling Principles and Applications》(分子模拟的原理与应用),A. R. Leach ,(第二版),北京:兴国图书出版社,2003。
[6]《计算材料学》,[德]D.罗伯编著,项金钟,吴兴惠译,北京:化学工业出版社,2002。

半导体器件仿真的多尺度模型与计算方法下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!半导体器件的设计和优化需要多尺度模型和计算方法的支持。

多尺度计算与模拟在材料科学中的应用随着科技的不断发展,人们对材料科学的理解也越来越深入,在材料科学中,多尺度计算与模拟技术具有重要的应用价值。
多尺度计算与模拟技术,是一种通过各种不同尺度的计算和模拟手段,对材料进行多层次的描述、分析和预测的技术。
本文将就多尺度计算与模拟在材料科学中的应用进行探讨。
一、多尺度模拟技术的基本原理多尺度模拟技术是在不同层次上进行模拟,再在层次间建立相应的关联,从而可以得到材料的多层次描述。
这个过程是一个迭代的过程,其基本原理是将材料的宏观行为分解为微观行为,从而获得材料的更全面和更深入的了解。
在多尺度模拟中,对材料的描述可以从宏观到微观多个层次上进行,如:材料的晶体结构、晶界、空隙、杂质和缺陷等;同时,可以根据不同的应用需求和研究对象,将材料定义为不同的尺度下的研究对象,如宏观尺度下的构件、中尺度下的材料组合、微观尺度下的单晶等。
在多尺度模拟中,材料的基本描述可以从量子力学范畴到力学方程范畴,在这个过程中,不同尺度下的模拟方法通常包括了不同的模型和理论,需用到多种计算方法和软件,如蒙特卡罗、分子动力学、密度泛函理论、有限元等。
二、多尺度模拟技术的应用场景1、材料表面的纳米结构设计表面介观尺度结构的改变可以极大的影响材料的力学、热学和光学等性质。
因此,纳米结构设计可以被用于一些特殊的需求,如能源储存和转换等现代技术。
例如,在金属的表面上定向生长纳米小颗粒可以使材料表面的光感诱导反应得到明显提高,因此可以用于太阳能电池、催化反应等领域。
2、晶界和缺陷的形成和演化晶界和缺陷是影响材料力学性质的关键因素,多尺度计算可以在不同尺度上刻画晶格缺陷对材料的影响。
例如,晶界的渗透会导致生长过程中的偏析现象,而在多尺度计算中,可以通过手动引入一个晶界来模拟晶界对物质输运和晶体相界面等方面的影响。
3、材料疲劳行为的预测钢材等材料在循环载荷下容易产生疲劳现象,而使用多尺度计算和模拟,可以预测疲劳行为的形成机制,并且为疲劳破坏预报提供有力的理论支持。
多尺度模拟技术在材料研究中的应用多尺度模拟技术是近年来材料科学领域中一项重要的研究工具和方法。
它通过将微观层面和宏观层面相结合,可以解决材料研究中存在的一些难题,为人们提供更加全面深入的材料结构和性能的认识,有助于推动材料科学领域的发展。
本文将从多尺度模拟技术的原理、应用和发展趋势等方面入手,深入探讨这项技术在材料研究中的应用。
一、多尺度模拟技术的原理多尺度模拟技术是一种将不同层次、不同尺度的信息进行有效融合的方法。
其基本原理是将微观尺度上的原子、分子等精细结构和宏观尺度上的宏观物理性质进行有效耦合,建立起一个多层次、多尺度的物理模型,通过计算机模拟,实现从原子水平到宏观水平的连续和一致性。
实现这一目标的主要手段包括尺度转换、信息传递和耦合方法等。
二、多尺度模拟技术在材料研究中的应用(一)材料结构与性能分析多尺度模拟技术可以有效模拟出材料的原子结构、分子结构以及材料的宏观结构和性能,可以帮助人们进一步探究材料的结构与性能之间的关系,从而指导材料的设计和制备工作。
例如,在纳米材料的研究中,多尺度模拟可以模拟出纳米材料的结构,在原子和分子级别上研究纳米材料的物理性质。
模拟结果可以揭示纳米材料的结构缺陷形成机制,从而改进纳米材料的制备方法,提高其性能。
(二)高温、高压下材料行为研究多尺度模拟技术可以模拟高温、高压、高辐射等极端条件下材料的行为,从而研究材料的物理和化学行为特性。
例如,在科学家们研究地球内部的构成和演化过程时,多尺度模拟技术被用于模拟地球内部材料的性质。
模拟结果发现,这些材料在极端的温度和压力条件下会发生多种相变,从而对地球内部的构成和演化过程造成重大影响。
(三)材料制备和加工过程的控制与优化多尺度模拟技术也可以被应用于材料制备和加工等过程中。
利用多尺度模拟技术可以模拟出材料的微观结构和性质,从而制定合理的制备和加工策略,优化材料的制备和加工过程,提高材料性能。
例如,在材料的表面处理及涂层制备过程中,多尺度模拟技术可以模拟表面处理过程中,不同物质间的相互作用原理,从而指导涂层制备过程,提高表面性能。
材料科学与工程中的多尺度建模技术多尺度建模技术是材料科学与工程领域中的一个重要研究方向。
随着现代科技的不断发展,材料科学与工程已经进入一个高度复杂的时代。
传统的材料研究方法已经不能够满足实际需求,因此多尺度建模技术的应用越来越广泛,成为了目前材料科学与工程领域中的热门议题。
多尺度建模技术是一种基于物理规律和数学方法的高度细致化建模技术。
该技术可以将材料的各种物理和化学过程从微观、介观、宏观各个尺度上进行建模和仿真,进而实现对材料性能和结构的预测和优化。
多尺度建模技术可以有效地提高材料研究的效率和准确度,同时还可以为材料工程实践提供较为精确的设计指导。
从微观尺度上看,多尺度建模技术主要运用分子动力学、量子化学和原子力显微镜等技术对材料的原子结构和动力学行为进行研究。
这些方法可以揭示材料微观结构和物理性质之间的关系,同时还可以研究各种小的结构缺陷、碎屑和化学反应的影响。
微观尺度的研究可以帮助我们更好地理解材料的结构和性能,为后续的宏观建模提供了重要的基础。
在介观尺度上,多尺度建模技术主要涉及晶体学、组织学、纳米结构控制和微观力学等方面。
这些方法主要用于模拟材料中的结晶、位错、相变等现象。
通过介观尺度以及上述的微观尺度的工作,研究人员可以掌握材料的完整结构与物理行为,为精细计算提供重要的条件。
在宏观尺度上,多尺度建模技术主要运用传统的材料力学、热力学和流体力学等物理学方法。
这些方法可以研究材料的整体力学性和热力学特性。
此外,材料的外观、几何结构等因素也会对材料的性能产生影响,并且这些因素也是材料宏观尺度建模的重要内容。
通过宏观尺度上的建模,研究人员可以为材料工程提供直接的应用价值,如钢铁、混凝土、建筑材料等工程中的材料。
在材料科学与工程中,多尺度建模技术的应用范围非常广泛。
例如,在钢铁工程中,它可以协助铁水的脱碳和净化过程。
在半导体工程中,多尺度建模技术可以为芯片设计优化提供以下数据。
在医学领域,多尺度建模技术可以帮助研究与治疗骨骼疾病相关的因素等等;在航空航天工程领域,多尺度建模技术可以模拟材料对高温、高压和极端环境下的抵御和适应性,以及攻坚雷达和飞机等设备的研究。
sjtu实变函数实变函数是数学较为高阶且难度较大的一个学科,其内容涉及到数学分析、微积分等多个领域。
上海交通大学(简称SJTU)作为我国顶尖学府之一,在实变函数的研究和应用上也有着很高的研究水平和学术地位。
在SJTU的实变函数教学中,首先会对实变函数的基本概念、性质、定理、证明方法等进行详细的阐述。
学生需要掌握实变函数的基础知识,如上极限、下极限、无穷小、无穷大、一致连续等,才能够进一步分析和理解实变函数的高层次内容。
另外,SJTU的实变函数课程也注重培养学生的数学思维和证明能力,学生需要熟练掌握证明方法,学习证明思路,强化数学逻辑,从而能够在数学研究和应用中更好地运用实变函数知识。
SJTU的实变函数教学不仅注重基础理论的掌握,也融入了实践应用环节。
在实际应用中,实变函数常常被用来求极限、优化问题、微积分、偏微分方程、调和分析、泛函分析等。
SJTU的教师们注重将实变函数理论与实际问题相结合,并引导学生进行相关的问题求解和研究。
这种理论与实践相结合的教学模式有利于学生更好地学习和运用实变函数知识。
除了教学方面,SJTU还在实变函数领域开展了许多研究和成果。
其实变函数研究团队在实变函数领域具有很高的学术地位,该团队在实变函数和拓扑学、调和分析等领域都有着较为出色的研究成果。
例如,该团队的研究人员蔡元培教授被誉为全球实变函数领域的大师。
他在实变函数领域的研究开创了全新的方向,提出了一系列有影响力的研究结论,并培养了一批优秀的学生。
除此之外,SJTU的实变函数研究团队还积极参与国际合作和学术交流。
例如,该团队的蔡元培教授曾多次受邀参加在国际上举办的学术会议,并发表了多篇具有重要影响的研究论文。
这也为SJTU的实变函数研究和教学提高了很高的学术影响力和国际地位。
综上所述,SJTU在实变函数教学和研究方面有着很高的学术水平和成就。
未来,SJTU的实变函数领域仍将继续加强教学和研究,加强国际交流,从而更好地为推动我国数学学科的发展和提高做出贡献。
计算材料科学中的多尺度模拟随着计算机技术和计算模拟技术的发展,计算材料科学不断引起人们的关注。
多尺度模拟具有将不同尺度的物理规律有效地整合在一起的能力,因此被视为应用于计算材料科学的一种强大工具。
本文将讨论多尺度模拟在计算材料科学中的应用和发展趋势。
1. 什么是多尺度模拟?多尺度模拟是一种用于描述物质在不同尺度下的行为和性质的模拟方法。
不同的尺度之间存在着不同的物理规律,因此需要采用不同的理论来解释不同尺度下的现象。
多尺度模拟的目的是将这些不同尺度的物理规律有效地整合在一起,以提高研究物质的效率和精度。
多尺度模拟通常包括从原子、分子、纳米尺度到宏观尺度的各个层次,涵盖了材料科学中热力学、动力学、结构和力学等领域。
不同的尺度对应着不同的物理规律和计算方法,如分子动力学、Monte Carlo模拟、有限元分析等。
2. 多尺度模拟在计算材料科学中的应用多尺度模拟在计算材料科学中具有广泛的应用,包括材料结构、材料强度、材料相变、介观结构等方面。
在材料结构方面,多尺度模拟可以通过从原子到宏观的不同尺度模拟来确定材料的微观组成和结构,以便更好地理解材料的性质和行为。
其中,分子动力学模拟可以用来研究材料的原子结构和动力学行为,而扩散反应模拟可以用来研究材料的表面反应和传输。
在材料强度方面,多尺度模拟可以通过模拟材料的变形和破裂行为来分析材料的力学性能和强度。
其中,有限元分析可以用来模拟宏观材料的力学行为,而分子动力学模拟可以用来模拟材料的原子层面上的力学行为。
在材料相变方面,多尺度模拟可以用来研究材料在相变过程中的结构和力学行为。
其中,Monte Carlo模拟可以用来模拟材料的相变过程,而分子动力学模拟可以用来模拟相变过程中原子的动力学行为。
在介观结构方面,多尺度模拟可以用来模拟和分析材料的介观结构和性质。
其中,相场模拟可以用来模拟材料的形态演化以及晶界、孪晶等介观结构的形成和演化,而格子Boltzmann方法可以用来模拟材料的传热和传质行为。
材料物理学中的多尺度模拟方法一、介绍材料物理学是研究物质各种性质和变化机制的科学。
多尺度模拟方法是材料物理学研究的基础工具之一,通过不同尺度模拟,可以更深入地理解材料本质和物理机理。
本文将介绍材料物理学中的多尺度模拟方法及其应用。
二、理论基础多尺度模拟方法基于材料的分子结构,将材料分为不同尺度的部分进行模拟。
通常使用的多尺度模拟方法有从第一性原理计算到材料微观结构分析的多层次模拟方法(MLM),分子动力学模拟(MD)、蒙特卡罗模拟(MC)等。
1.第一性原理计算第一性原理计算是通过量子力学基本原理对材料进行计算,不假设任何经验参数,因此对于复杂物质的计算具有很大的优势。
通过计算材料的电子结构、热力学性质、光电材料性质等参数,可以得到材料的理论性能。
同时,第一性原理计算也是多尺度模拟方法的基础,因为材料的宏观性质是由其分子结构和粗大中的作用相互影响的。
2.分子动力学模拟分子动力学模拟是一种基于牛顿运动定律进行的模拟方法,通过对材料组成部分的运动进行模拟来预测材料的行为和稳定性。
分子动力学模拟可以在原子或分子水平上解释材料性能,在材料制备、加工、使用等不同阶段的问题上发挥了重要的作用。
3.蒙特卡罗模拟蒙特卡罗模拟是基于随机采样的一种模拟方法,其核心思想是允许材料结构中的离子、分子在空间中运动,通过跳跃式的方法计算材料在温度、压力等条件下的性质变化。
三、应用多尺度模拟方法可以用于材料表面特性、力学性质、热力学性质、化学反应性质等多个领域的研究。
以下是几个应用案例。
1.材料表面特性表面结构影响了材料与其他材料的接触和与环境相互作用的方式。
通过对表面结构进行多尺度模拟,可以理解材料表面的原子结构、表面能、表面反应动力学等性质。
2.力学性质材料的力学性质在制备过程中和使用过程中都起着关键作用。
通过多尺度模拟,可以预测材料在应力场下的弹性和塑性变形、力学失稳的机制等,同时也可以对材料所受到的力进行详细分析,为设计材料提供数据支持。
华东师范大学2018年物理与材料科学学院理论物理专业简介概况物理系理论物理专业培养博士和硕士两个层次的研究生,分理论、数值计算、以及理论与数值模拟结合三个不同的培养模式。
主要目标是:培养具有坚实的物理基础,掌握熟练的数值模拟技术,站在学科发展前沿,能独立从事科学研究、高等教育、技术研发与管理等高层次、全面发展型专业人才。
独特的培养模式(博士生):1.宽口径培养:理论研究和数值模拟联合培养;2.国际联合培养:中法联合培养项目(国外、国内双学位),自由联合培养(1-2年国外研究机会,国内拿学位)。
学科基础与研究环境:本学科依托于物理系、理论物理研究所。
团队承担有多项国家级科研项目,包括多项国家自然科学基金重点项目、面上项目、青年项目,及多项国家教委与上海市人才计划项目(新世纪人才计划、曙光计划、浦江计划)等。
本学科导师团队成员均具有国外留学经历与背景,建立了广泛的国际合作关系。
与我们有长期合作的国外科研机构包括,美国、德国、法国、新加坡、意大利、日本、巴西等十多个国家的很多研究机构。
我们会不定期地邀请这些国外机构的知名专家学者前来短期访问,讲学。
这些专家不仅给研究生带来了一系列精彩的学术报告,并在报告后耐心的与研究生进行学术交流与探讨,同时也为研究生打开国际视野,提供国外学习与研究的机会奠定基础。
本学科专业有较为宽阔的就业机会。
我们毕业的博士生有成为高等院校教师、中科院研究所科研人员,技术公司研发工程师等,也有学生出国进行博士后研究的。
硕士毕业后多数去国外攻读博士学位,部分有从事教师、公司技术人员等。
到目前为止,我们专业培养了很多优秀的研究生。
值得一提是2016年毕业生张希昀同学与2017年毕业的毕宏杰同学均以第一作者在国际顶尖的物理学期刊《Physical Review Letters》上发表了论文。
到目前为止,所有已毕业的十多位博士生同学全部有出国留学经历。
顾长贵同学已获上海市东方学者,唐明同学已获华东师大紫江青年学者。
Dislocation and Stacking Fault
Name:Wu lingling(user023) Student number:016050910054
1 Calculations of Lattice constant and volume modulus
Using molecular dynamics,we can simulate crystals in edge dislocation,screw dislocations and stacking fault, also we can calculate the dislocation strain energy and dislocations. Comparing the method of molecular dynamics calculation values and theoretical, we can analysis its error.Through this experiment, deepen para fault, fault, and the understanding of molecular dynamics simulation.
For edge dislocation, strain for per unit length:
20ln
4(1)e e
Gb R
E r πn =−
For a screw dislocation, strain for per unit length:
20ln
4s
e
Gb R E r π
= Molecular dynamics is dislocation of strain energy method:
()/MD dislocated ref E E E L
=−
In actual crystal structure, the closed normal stacking sequence may be damaged and staggered,
which named the stacking fault.Cambium mistake almost do not produce lattice distortion, but it undermines the integrity of the crystal and the normal cyclical, anomalous diffraction effect in the electronic, allowing the energy of the crystal increased, this part of the increased energy is called the stacking fault energy.
The mathod using Molecular dynamics to calculation approach stacking fault:
SFE =
tot ref
E E S
γ−
2 Results and Analysis
2.1 helical dislocation
-91512.1172811518-(-91519.9264975819)7.80921643s
E ev =
e
l =4.45685A A
,so
57.80921643 1.5326.0/7A 3A 95s s e
s
E ev
E ev l ===A A When calculating Cu,0 3.639A a =A
,
0/2b a =,43.55G GPa =,we can get the result:
20
ln 0.6595(/A)
4s e
Gb R
E ev r π==A
2.2 stacking fault
-91512.1172811518-(-91519.9264975819)7.80921643s
E ev =
e
l =5.09537A A
When calculating Cu,0 3.639A a =A
,0/2b a =,43.55G GPa =, we can get the
result:
20
ln 0.6595(/A)
4s e
Gb R
E ev r π==A
2.3 stacking fault
E=
2
44.0461825440018(mJ/m )
For edge dislocation,when chocing x1=[6.81205 126.341 109.114] A and x2=[6.87178 126.333 141.831] A ,we can get 141.831109.11432.717A d −==A
,so
2102 1.30(10/)81s b J m m n πn −+•=−,2
2
21=39.7347(/)81s b mJ m d
m n γπn +••=− For helical dislocation,when chocing x1=[127.087 125.957 2.27685] A ,x2=[137.353 124.044 1.02476] A ,we can get 137.353127.08710.266A d −==A
,so
210
230.585(10/)81s b J m m n πn −−•=−,222-31=56.9842(/)81s b mJ m d m n γπn ••=−.
3 Summary form。