电路理论习题解答第4章

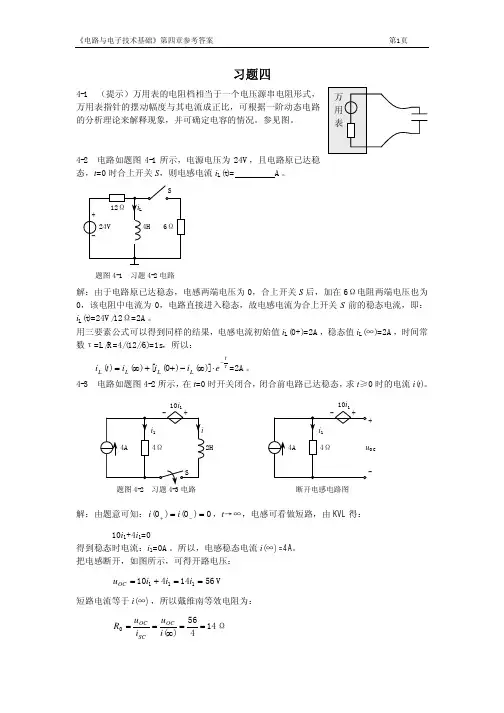
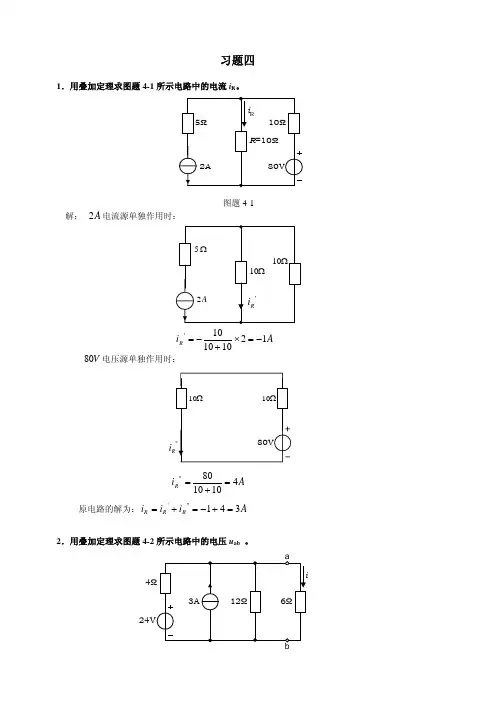
习题四1．用叠加定理求图题4-1所示电路中的电流i R 。

图题4-1解： A 2电流源单独作用时：A i R 12101010'−=×+−=V 80电压源单独作用时：i A i R 4101080''=+=原电路的解为：A i i i R R R 341'''=+−=+=2．用叠加定理求图题4-2所示电路中的电压u ab 。

4图题4-2解：V 24电压源单独作用时：Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时：Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为：V u u u ab ab ab 18612'''=+=+=3．用叠加定理求图题4-3所示电路中的电流i 。

6A图题4-3解： A 6电流源单独作用时：ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时：Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为：()()A i i i 624'''−=−+−=+=4．图题4-4所示电路中，R =6Ω，求R 消耗的功率。

图题4-4解： 将R 支路以外的部分看作一个二端电路。

可采用叠加原理求oc u ：12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻：eqRΩ=++×=426363eq R 原电路简化为：Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5．图题4-5所示电路中， R 1=1.5Ω R 2=2Ω，求（a ）从a、b 端看进去的等效电阻；（b ）i 1与i s 的函数关系。

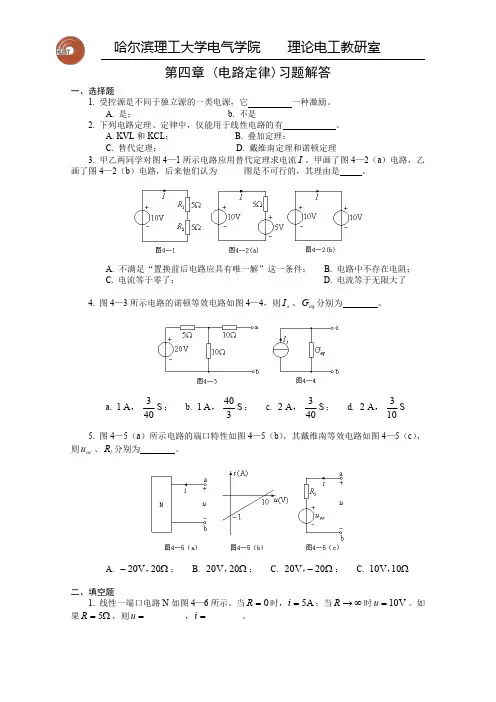
第四章(电路定律)习题解答一、选择题1.受控源是不同于独立源的一类电源，它一种激励。

A.是； b.不是2.下列电路定理、定律中，仅能用于线性电路的有。

A.KVL 和KCL ； B.叠加定理；C.替代定理； D.戴维南定理和诺顿定理3.甲乙两同学对图4—1所示电路应用替代定理求电流I 。

甲画了图4—2（a ）电路，乙画了图4—2（b ）电路，后来他们认为图是不可行的，其理由是。

A.不满足“置换前后电路应具有唯一解”这一条件；B.电路中不存在电阻；C.电流等于零了；D.电流等于无限大了4.图4—3所示电路的诺顿等效电路如图4—4，则s I 、eq G 分别为。

a.S 403A 1，；b.S 340A 1，；c.S 403A 2，；d.S 103A 2，5.图4—5（a ）所示电路的端口特性如图4—5（b ），其戴维南等效电路如图4—5（c ），则oc u 、i R 分别为。

A.Ω-20V 20，；B.Ω20V 20，；C.Ω-20V 20，； C.Ω10V 10，二、填空题1.线性一端口电路N 如图4—6所示。

当0=R 时，A 5=i ；当∞→R 时V 10=u 。

如果Ω=5R ，则=u ，=i 。

2.图4—7所示电路中，N 为线性电路，且Ω=10R 。

当0=s u ，0=s i 时，V 5=u ；当A 2=s i ，0=s u 时，V 8=u ；当0=s i ，V 10=s u 时，V 6=u 。

那么，当A 6=s i ，V 4=s u 时，=i 。

3.图4—8（a ）所示电路的戴维南等效电路如图4—8（b ），那么=s U ，=eq R 。

4.图4—9（a ）所示电路的戴维南等效电路如图4—9（b ），则=s U ，=eq R 。

5.在图4—10（a ）所示的电路中，i u 1024-=(i 的单位用安培时，u 的单位为伏特)，其戴维南等效电路如图4—10（b ），则=s u ，=0R 。

三、计算题1.用叠加定理计算图4—11所示电路中的u 。

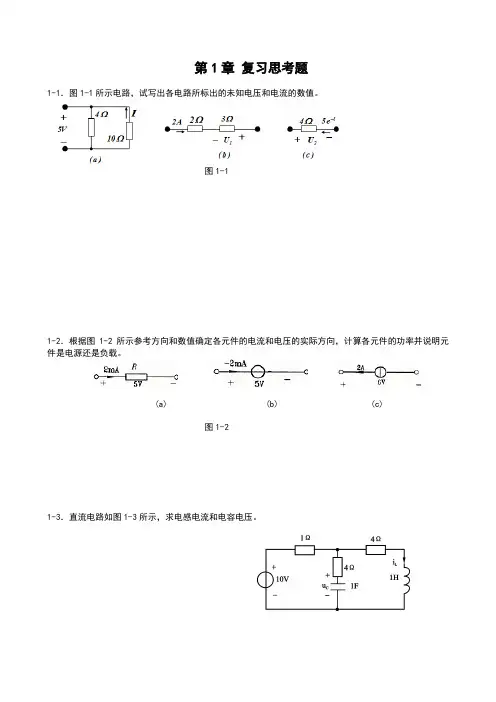
第1章复习思考题1-1．图1-1所示电路，试写出各电路所标出的未知电压和电流的数值。

图1-11-2．根据图1-2所示参考方向和数值确定各元件的电流和电压的实际方向，计算各元件的功率并说明元件是电源还是负载。

(a) (b) (c)图1-21-3．直流电路如图1-3所示，求电感电流和电容电压。

图1-31-4．如图1-4所示，电路中包含的各个元件的电压和电流参考方向如图所示，其中100P 1=W ，10P 2-=W ，50P 3=W ，20P 4=W ，求5P ，元件5是电源还是负载？图1-41-5．求图1-5所示电路中的电压1u 和1i 。

图1-51-6．求图1-6所示电路中的电压u 。

3Ω2Ω4Ωi10 V图1-61-7．求图1-7所示电路中的电压U 。

2ΩU4Ω+ -+ -+- +- 5V2V 5V 1Aa bde图1-71-8．图1-8所示电路中，已知5u ab -=V ，求电压源电压s u 。

图1-81-9．电路如图1-9所示，试求电压U X 。

图1-91-10．如图1-10所示的图，如果选1、2、3、4、8支路为树，则其基本回路组是什么？如果选择自然网孔为基本回路组，则其对应的树由哪些支路组成？②⑤1 2 3 4610 ④89 ⑥57 ③图1-10第2章复习思考题2-1．写出题2 1图所示各电路的端口电压电流的伏安特性方程。

(a) (b)图2-12-2．电路如图2-2(a)、(b)、(c)、(d)、(e)和(f)所示，试计算a、b两端的电阻，其中电阻R=8。

(a) (b)(c)(d)(e) (f)图2-22-3． 利用电源等效变换，化简图2-3(a)和(b)的一端口网络。

(a) (b)图2-32-4．利用电源的等效变换求图示2-4电路中的电流I 。

图2-42Ω6V+I2Ω 2A7Ω6A2Ω2-5．求图2-5电路中的受控电流源的功率。

图2-5 2-6．求图2-6各电路的输入电阻R in。

图2-6第3章复习思考题3-1．用支路电流法求图3-1所示电路中各支路电流及各电阻上吸收的功率。

教材习题4答案部分（p126）答案解：将和改写为余弦函数的标准形式，即电压、电流的有效值为初相位相位差；与同相；与正交，超前于答案答案解：(a)利用正弦量的相量表示法的线性性质得：(b)磁通相量通常用最大值表示，利用正弦量的相量表示法的微分性质得：(c) 利用正弦量的相量表示法的线性性质与微分性质得：答案解：电压表和电流表读数为有效值，其比值为阻抗模，即将已知条件代入，得联立方程，解得答案解：(a) RC串联电路中电阻电压与电容电压相位正交，各电压有效值关系为电流的有效值为(b)RC并联电路中电阻电流与电容电流相位正交，总电流有效值为(c)由并联电容、电感上电流相位相反，总电流为电阻电压与电容电压相位正交，总电压为：答案略答案解：设，则所求电流有效值为。

答案解：电压源和电流源的相量分别为对节点①和②列相量形式节点电压方程由图可知受控源控制量解得受控电流源的电压为答案解：相量模型如图(b)所示。

对节点①、②列节点电压方程：(1)(2)联立解得又因为所以即越前于的相位差为。

答案解：对含运算放大器的电路宜列写节点电压方程：(1)(2)由端口特性得(3)将式(2)(3)代入(1)得输出电压瞬时值为答案解：图示电路容抗，列节点电压方程（1）将代入(1)式解得电流答案解：由阻抗的串、并联等效化简规则得当时，由上式得，且与频率无关。

答案解：(1)求开路电压对图(a)电路列节点电压方程受控源控制量即为节点电压，即(3)将式(3)代入式(2)再与式(1)联立解得，(2)求等效阻抗在ab端外施电压源，求输入电流，与的比值即为等效阻抗。

由节点②得又答案解：对图(a)电路做戴维南等效，如图(b)所示。

(1)(2)由图(b)可知，当时，电阻两端电压与电阻无关，始终等于。

由式(1)解得将式(3)代入式(2)得答案解：先对图(a)电路ab端左侧电路作戴维南等效，如图(b)所示。

令得等效阻抗由知，欲使电流有效值为最大，电容的量值须使回路阻抗虚部为零，即：等效后电路如图(b)所示。

第四章电路定律1. 内容提要电路定理是电路理论的重要组成部分，为求解电路问题提供了另一种分析方法，这些方法具有比较灵活，变换形式多样，目的性强的特点。

因此相对来说比第三章中的方法较难掌握一些，但应用正确，将使得一些看似复杂的问题的求解过程变得非常简单。

应用定理分析电路问题必须做到理解其内容，注意使用的范围、条件，熟练掌握使用的方法和步骤。

需要指出，在很多问题中定理和方程法往往又是结合使用的。

2. 重点和难点(1) 掌握各种定理的适用范围；(2) 叠加定理中受控源与独立电源的不同作用；(3) 戴维南-诺顿等效电路的求解、特别是等效电阻的求解方法；(4) 应用特勒根定理与互易定理时，注意电路的特征。

3. 典型例题分析【例题1】：叠加定理的应用。

求图4.1所示电路中的电压U。

图4.1解：当12V电压源单独作用时，电流源等于零即相当于开路，画出电路如图4.1.1所示，应用分压原理有：U‘= = 4V当3A电流源单独作用时，电压源等于零即相当于短路，画出电路如图4.1.2所示，应用分流公式得：U‘‘= (6//3) 3= 6V图4.1.1 图4.1.2则所求电压：U = U‘+ U‘‘=4+6=10V.【例题2】：含有受控源的电路，在应用叠加定理时，受控源始终保留在分电路中。

计算图4.2所示电路的电压u电流i 。

图4.2解：应用叠加定理求解。

当10V电源单独作用时的等效电路如图4.2.1所示：图4.2.1 图4.2.2∵∴解得：；。

当5A电源单独作用时的等效电路如图4.2.2所示，由左边回路的KVL：。

解得：，，所以：，【例题3】：在使用叠加定理时，要注意其适用条件的应用。

本例给出了研究激励和响应关系的实验方法。

封装好的电路如图4.3所示，已知下列实验数据：图4.3当U S=1V，i S=1A时，响应i=2A；当U S=-1V，i S=2A时，响应i=1A；求：U S=-3V，I S=5A时，响应i=？。

电路理论练习参考解答§3、线性电阻电路1）、对第一小节中的电路，假定g1=g2=…=g10=1s，求节点1、3与地之间形成的二端口(不包括图中的电流源)的开路阻抗矩阵。

解：将各g 的值代入节点电压方程，先在节点1注入单位电流源，有：[]100000Tn n Y V ⋅=其中210100021100012001100310100031001013n Y −−⎡⎤⎢⎥−−⎢⎥⎢⎥−−=⎢⎥−−⎢⎥⎢⎥−−⎢⎥−−⎣⎦解出上述方程，得[0.8833 0.3500 0.2833 0.4167 0.3667 0.2167]n V =T ， 因此0.8833，0.2833。

再在节点3注入单位电流源，节点电压方程成为：11z =21z =[]001000Tn n Y V ⋅=解[0.45 0.65 1.05 0.25 0.30 0.45]n V =T 故0.45， 1.05，从而12z =22z =0.88330.28330.451.05oc Z ⎡⎤=⎢⎥⎣⎦2）、试推导二端口从y 参数到传输参数的转换式。

解：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−Δ−−−=⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡⇒⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡−=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−⎥⎦⎤⎢⎣⎡−⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−⎥⎦⎤⎢⎣⎡−⇒⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡−21112121212222221212111112222121121112211222112112121222112112122211211211100110010100101001y y y y y y y i v y y y y i v i v y y i v y y i v i v y y y y i i v v y y y y v v y y y y i i ；即得传输参数表达，其中，11221221y y y y y Δ=−。

第4章三相电路【基本要求】掌握三相四线制中三相负载的正确联接。

了解中线的作用；掌握对称星形和三角形联接时相线电压、相线电流在对称三相电路中的相互关系；掌握对称三相电路电压、电流和功率的计算。

了解安全用电常识，触电方式及其防护、接地和接零保护以及静电防护与电气防火防爆。

【重点】对称三相负载星形、三角形联接的三相对称电路分析，相线电压、相线电流的关系以及三相电路功率的计算。

【难点】各电压、电流相位的确定以及非对称三相电路分析。

4.1 基本理论1. 三相正弦交流电由三相交流发电机产生，经升压变压器输送至电网，再输送到各地变电所，经降压后到用户。

由发电厂到电网将交流电压升高是为了降低电网传输时的功率损耗；由电网到用户的降压则是为了保障人身和设备的安全。

2. 由三条相线和一条中性线向用户供电的电源称三相四线制电源。

三相四线制电源可提供相、线电压两种电压，且U L=√3U P，线电压相位比对应相电压超前30º。

3. 负载接于三相电源时必须遵循两个原则：一是加于负载的电压必须等于负载的额定电压；二是尽可能使电源的三相负载对称。

根据此两项原则，三相负载可接成星形或三角形。

当负载的额定相电压等于电源相电压时，负载接成星形；当负载的额定相电压等于电源线电压时，负载接成三角形。

4. 负载作星形连接时，I L=I P，当负载对称或负载不对称作Y O（三相四线制）连接时，负载的相电压即电源的相电压，与电源的线电压U L间保持U L=√3U P、相位超前30º关系。

若负载不对称作Y形（三相三相制，无中线）连接时，则以上关系不存在。

可见，中线的作用是不论负载是否对称，可使三相负载的相电压保持对称。

5. 负载作三角形连接时，负载的相电压为电源的线电压，即U P=U L，当负载对称时，I L=√3I P、线电流相位滞后对应的相电流30º。

当负载不对称时，不存在上述关系。

6. 三相负载的有功功率和无功功率分别等于每相负载的有功功率和无功功率之和，即P=P A+P B+P CQ=Q A+Q B+Q CS=√P2+Q2C若负载对称时，则有如下计算公式P=3U P I P cosϕ=√3U L I L cosϕQ=3U P I P sinϕ=√3U L I L sinϕS=√P2+Q2=3U P I P=√3U L I L上式对星形联接和三角形联接的三相负载均适用。

第四章 电路定理电路定理是电路理论的重要组成部分，为我们求解电路问题提供了另一种分析方法，这些方法具有比较灵活，变换形式多样，目的性强的特点。

因此相对来说比第三章中的方程式法较难掌握一些，但应用正确，将使一些看似复杂的问题的求解过程变得非常简单。

应用定理分析电路问题必须做到理解其内容，注意使用的范围、条件，熟练掌握使用的方法和步骤。

需要指出，在很多问题中定理和方程法往往又是结合使用的。

4-1 应用叠加定理求图示电路中电压ab u 。

解：首先画出两个电源单独作用式的分电路入题解4-1图（a ）和（b ）所示。

对（a ）图应用结点电压法可得1sin 5)121311(1t u n =+++ 解得 15sin 3sin 53n t u t V== (1)111113sin sin 2133n ab n u u u t t V=⨯==⨯=+对（b ）图，应用电阻的分流公式有1132111135t t e i e A--+=⨯=++所以 (2)110.25t t ab u i e e V--=⨯==故由叠加定理得(1)(2)sin 0.2t ab ab ab u u u t e V -=+=+4-2 应用叠加定理求图示电路中电压u 。

解：画出电源分别作用的分电路如题解（a ）和（b ）所示。

对（a ）图应用结点电压法有105028136)101401281(1++=+++n u解得(1)113.650.10.0250.1n u u +==++ 18.624882.6670.2253V===对（b ）图，应用电阻串并联化简方法，可求得10402(8)32161040331040183(8)21040si u V ⨯⨯++=⨯=⨯=⨯+++ (2)16182323si u u V-==-⨯=-所以，由叠加定理得原电路的u 为(1)(2)24888033u u u V =+=-=4-3 应用叠加定理求图示电路中电压2u 。

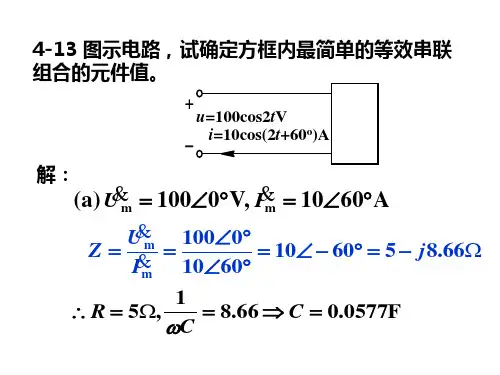
电路理论第四章习题答案P1294.2电路如图4・51所示，若电压源的电压＞ W,则电路的功率情况是怎 样的？若S 〉1V 则 M "1•:弘"1 V 。

（产生）P R = U s • ip > 0 （吸收） RA = -U^x\A=-U c <0 /寺牛、:.-U （lh +5Z 2+3X 2A-8V + 2X 2A = 0/. U ah =4 + 5x3 + 3x2-8 = 177解:参考点选在对①(4 + 3X7,-4173 =-8-3x1对④点-5SU 3 4-1/4 (1+5)= 8A - 25 AU 3 = 22V U { , U 2 =5V :,U n =U }-U 2=\W4.10已知线性含源单口网络与外电路相连，如图4・59所示，且已知ab 端口 电压〃 = 12.5V,而“b 端口的短路电流I sc=^A ，试求岀单口网络N 的戴维南 等效电路。

解：设“b 的左边等效为和心的串联：电路如图4-58所示，求节点①和节点②之间的电 网络N 也用"oc 和心等效n 解：i 2=\A^iU. 4.5图4・54,求a,b 两点间的电压Uab则2A 流过2。

ir= 2A — （—!）=3A当端口短路时： 40 U/ =/ +人二冷_ +』1 = 10〃必sc 1 2 5 R （）~3由①、②nUdW R° =5K04.12已知线性电阻网络如图4-61,半2A 电流源没接入吋，3A 电流源对网 络提供功率54W,且已知匕=12卩，当3A 电流源，没接入时，2A 电流源对网 络提供28W 功率且知：U 3=SV1） 求两电源同时接入时，各电源的功率。

2） 确定网络N 最简单的一种结构和元件参数值。

解：当3A 作用，含量用列），⑴）表示t/P = 12V当2A 单独作用时,分量用呼，於）表示当两电源共同作用时,-=科）+砧）=12V + 14心26V [73=[/p ）+^2） = l8 + 8V= 26VP 2A = _2 A x ”2 = _2 x 26 = _52（w ）P 34 = -3A x [/3 =-3x26 = -78（vv ）2）•••匕式厲，用如下网络代替i = 2A + 3A = 5A{2X R X +R 7X 5A = U 2=26V且已知为2A 单独作用吋：［/（2）= 14V, = 8VR x = 同理3A 单独作用吋：列）= 12U, U^} = \SV3A 3R z = 4Q4.13 No 为无源线性电阻网络，R ］可调，R2固定，当Us=8V 时，R 】=0时， I 2=0.2A ；当逐渐增大R I 值时,使X0.5A 时,&端电压U ）=5V,如图4-62（a ）所 示,当Us=20V 时,变化R ］值,使b=2A,如图4-62（b ）所示，试问此吋R ］端电P3AP2A ~2A 28 ~214V （〃炉-砂））二（14-8）“3a 2 2压3为何值。

第四章配电网运行分析习题和解答一、简答题1、配电网的电压降落、电压损耗和电压偏移指什么？答：电压降落是指线路首末两端电压的相量差。

电压损耗是指线路首末两端电压的数值差。

电压偏移是指线路首端或末端实际电压和线路额定电压的数值差。

2、配电网的损耗由哪些因素引起的？答：配电网的损耗是由两部分组成的：一部分是和传输功率有关的损耗，它产生在输电线路和变压器的串连阻抗上，传输功率愈大则损耗愈大，这种损耗叫变动损耗，在总损耗中所占比重较大；另一部分损耗则仅和电压有关，它产生在输电线路和变压器的并联导纳上，如输电线路的电晕损耗、变压器的励磁损耗等，这种损耗叫固定损耗。

3、配电网的网损率指什么？答：在同一时间内，配电网的电能损耗占供电量的百分比，称为配电网的损耗率，简称网损率或线损率。

4、配电网的潮流计算指什么？答：配电网的潮流计算是根据配电网中已知的负荷及电源电压计算出其它节点的电压和元件上的功率分布。

5、电力系统中有哪些主要的无功电源？答：电力系统主要的无功电源包括同步发电机、调相机、电容器及静止无功补偿器、线路充电功率等。

6、电力系统无功功率平衡指什么？答：电力系统无功功率平衡包含两个含义。

首先是对于运行的各个设备，要求系统无功电源所发出的无功功率和系统无功负荷及无功损耗相平衡。

其次是对于一个实际系统或是在系统的规划设计中，要求系统无功电源设备容量和系统运行所需要的无功电源及系统的备用无功电源相平衡，以满足运行的可靠性及适应系统负荷发展的需要。

7、短路指什么？有哪些基本类型？答：短路就是供电系统中一相或多相载流导体接地或相互接触并产生超出规定值的大电流。

供电系统中短路的基本类型分三相短路、两相短路、单相接地短路和两相接地短路。

8、简述无穷大功率电源条件下短路电流的计算步骤。

答：无穷大功率电源条件下短路电流的计算步骤如下：（1）取功率基准值S，B并取各级电压基准值等于该级的平均额定电压。

（2）计算各元件的电抗标么值，并绘制出等值电路。

电路理论基础习题答案第一章1-1. (a)、(b)吸收10W ；(c)、(d)发出10W. 1-2. –1A; –10V; –1A; – 4mW.1-3. –0.5A; –6V; –15e –tV; 1.75cos2t A; 3Ω; 1.8cos 22t W.1-4. u =104 i ; u = -104 i ; u =2000i ; u = -104 i ;1-5.1-6. 0.1A. 1-7.1-8. 2F; 4C; 0; 4J. 1-9. 9.6V,0.192W, 1.152mJ; 16V, 0, 3.2mJ. 1-10. 1– e-106 tA , t >0 取s .1-11. 3H, 6(1– t )2 J; 3mH, 6(1–1000 t ) 2 mJ;1-12. 0.4F, 0 .1-13. 供12W; 吸40W;吸2W; (2V)供26W, (5A)吸10W.1-14. –40V, –1mA; –50V, –1mA; 50V, 1mA. 1-15. 0.5A,1W; 2A,4W; –1A, –2W; 1A,2W.1-16. 10V,50W;50V,250W;–3V,–15W;2V,10W. 1-17. (a)2V;R 耗4/3W;U S : –2/3W, I S : 2W; (b) –3V; R 耗3W; U S : –2W, I S :5W; (c)2V,–3V; R 耗4W;3W;U S :2W, I S :5W; 1-18. 24V, 发72W; 3A, 吸15W;24V 电压源; 3A ↓电流源或5/3Ω电阻. 1-19. 0,U S /R L ,U S ;U S /R 1 ,U S /R 1 , –U S R f /R 1 . 1-20. 6A, 4A, 2A, 1A, 4A; 8V, –10V, 18V. 1-21. K 打开：(a)0, 0, 0; (b)10V, 0, 10V; (c)10V,10V,0; K 闭合: (a)10V,4V,6V; (b)4V,4V,0; (c)4V,0,4V; 1-22. 2V; 7V; 3.25V; 2V. 1-23. 10Ω.1-24. 14V.1-25. –2.333V, 1.333A; 0.4V, 0.8A.1-26. 12V, 2A, –48W; –6V, 3A, –54W . ※第二章2-1. 2.5Ω; 1.6R ; 8/3Ω; 0.5R ; 4Ω; 1.448Ω; . R /8; 1.5Ω; 1.269Ω; 40Ω; 14Ω. 2-2. 11.11Ω; 8Ω; 12.5Ω. 2-3. 1.618Ω.2-4. 400V;363.6V;I A =.5A, 电流表及滑线电阻损坏. 2-6. 5k Ω. 2-7. 0.75Ω.2-8. 10/3A,1.2Ω;–5V,3Ω; 8V,4Ω; 0.5A,30/11Ω. 2-9. 1A,2Ω; 5V,2Ω; 2A; 2A; 2A,6Ω. 2-10. –75mA; –0.5A. 2-11. 6Ω; 7.5Ω; 0; 2.1Ω. 2-12. 4Ω; 1.5Ω; 2k Ω. 2-13. 5.333A; 4.286A. 2-14. (a) –1 A ↓; (b) –2 A ↓, 吸20W. 2-16. 3A. 2-17. 7.33V. 2-18. 86.76W. 2-19. 1V, 4W. 2-20. 64W.2-21. 15A, 11A, 17A. 2-23. 7V, 3A; 8V,1A. 2-24. 4V, 2.5V, 2V. 2-26. 60V. 2-27. 4.5V. 2-28. –18V.2-29. 原构成无解的矛盾方程组; (改后)4V,10V. 2-30. 3.33 k , 50 k . 2-31. R 3 (R 1 +R 2 ) i S /R 1 . 2-32. 可证明 I L =－ u S /R 3 . 2-33. –2 ; 4 .2-34. (u S1 + u S2 + u S3 )/3 . ※第三章3-1. –1+9=8V; 6+9=15V; sin t +0.2 e – t V. 3-2. 155V. 3-3. 190mA. 3-4. 1.8倍.3-5. 左供52W, 右供78W. 3-6. 1; 1A; 0.75A.3-7. 3A; 1.33mA; 1.5mA; 2/3A; 2A.iA 0 s 1 12 3 1-e -t t 0 t ms imA 4 10 0 t ms p mW 4 100 2 25 i , A 0.4 .75 t 0 .25 1.25 ms -0.4 (d) u , V 80 0 10-20 t , ms(f ) u , V 1000 10 t , ms (e)p (W) 100 1 2 t (s) -10编辑版word3-8. 20V, –75.38V.3-9. –1A; 2A; –17.3mA. 3-10. 5V, 20; –2V, 4. 3-12. 4.6. 3-13. 2V; 0.5A. 3-14. 10V, 5k .3-15. 4/3, 75W; 4/3, 4.69W. 3-16. 1, 2.25W. 3-18. 50. 3-19. 0.2A. 3-20. 1A. 3-21. 1.6V. 3-22. 4A; –2A. 3-23. 23.6V; 5A,10V. 3-24. 52V. ※第四章4-1. 141.1V, 100V, 50Hz, 0.02s,0o , –120o ; 120 o.4-2. 7.07/0 o A, 1/–45 o A, 18.75/–40.9 oA. 4-3. 3mU , 7.75mA .4-4. 10/53.13oA, 10/126.87oA, 10/–126.87oA,10/–53.13oA ；各瞬时表达式略。