电路理论习题解答第2章

第二章电阻电路的等效变换等效变换”在电路理论中是很重要的概念，电路等效变换的方法是电路问题分析中经常使用的方法。

所谓两个电路是互为等效的，是指（1）两个结构参数不同的电路再端子上有相同的电压、电流关系，因而可以互代换的部分）中的电压、电流和功率。

相代换；（2）代换的效果是不改变外电路（或电路中未由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。

等效的对象是外接电路（或电路未变化部分）中的电压、电流和功率。

等效变换的目的是简化电路，方便地求出需要求的结果。

深刻地理解“等效变换” 的思想，熟练掌握“等效变换”的方法在电路分析中是重要的。

2-1 电路如图所示，已知。

若：（1）；（2）；（3）。

试求以上3 种情况下电压和电流。

解：（1）和为并联，其等效电阻，则总电流分流有2）当，有3），有2-2 电路如图所示，其中电阻、电压源和电流源均为已知，且为正值。

求：（1）电压和电流；（2）若电阻增大，对哪些元件的电压、电流有影响？影响如何？解：（1）对于和来说，其余部分的电路可以用电流源等效代换，如题解图（a）所示。

因此有2）由于和电流源串接支路对其余电路来说可以等效为个电流源，如题解图（b）所示。

因此当增大，对及的电流和端电压都没有影响。

但增大，上的电压增大，将影响电流源两端的电压，因为显然随的增大而增大。

注：任意电路元件与理想电流源串联，均可将其等效为理想电压源，如本题中题解图（a）和（b）o但应该注意等效是对外部电路的等效。

图（a）和图b) 中电流源两端的电压就不等于原电路中电流源两端的电压。

同时，任意电路元件与理想电压源并联，均可将其等效为理想电压源，如本题中对而言，其余部分可以等效为，如题图（c）所示。

但等效是对外部电路（如）的等效，而图（c）中上的电流则不等于原电路的电流。

2-3 电路如图所示。

（1）求；（2）当时，可近似为，此时引起的相对误差为当为的100倍、10 倍时，分别计算此相对误差。

第1章习题解析一．填空题：1.电路通常由电源、负载和中间环节三个部分组成。

2.电力系统中，电路的功能是对发电厂发出的电能进行传输、分配和转换。

3. 电阻元件只具有单一耗能的电特性，电感元件只具有建立磁场储存磁能的电特性，电容元件只具有建立电场储存电能的电特性，它们都是理想电路元件。

4. 电路理论中，由理想电路元件构成的电路图称为与其相对应的实际电路的电路模型。

5. 电位的高低正负与参考点有关，是相对的量；电压是电路中产生电流的根本原因，其大小仅取决于电路中两点电位的差值，与参考点无关，是绝对的量6.串联电阻越多，串联等效电阻的数值越大，并联电阻越多，并联等效电阻的数值越小。

7.反映元件本身电压、电流约束关系的是欧姆定律；反映电路中任一结点上各电流之间约束关系的是KCL定律；反映电路中任一回路中各电压之间约束关系的是KVL定律。

8.负载上获得最大功率的条件是：负载电阻等于电源内阻。

9.电桥的平衡条件是：对臂电阻的乘积相等。

10.在没有独立源作用的电路中，受控源是无源元件；在受独立源产生的电量控制下，受控源是有源元件。

二．判断说法的正确与错误：1.电力系统的特点是高电压、大电流，电子技术电路的特点是低电压，小电流。

（错）2.理想电阻、理想电感和理想电容是电阻器、电感线圈和电容器的理想化和近似。

（对）3. 当实际电压源的内阻能视为零时，可按理想电压源处理。

（对）4.电压和电流都是既有大小又有方向的电量，因此它们都是矢量。

（错）5.压源模型处于开路状态时，其开路电压数值与它内部理想电压源的数值相等。

（对）6.电功率大的用电器，其消耗的电功也一定比电功率小的用电器多。

（错）7.两个电路等效，说明它们对其内部作用效果完全相同。

（错）8.对电路中的任意结点而言，流入结点的电流与流出该结点的电流必定相同。

（对）9．基尔霍夫电压定律仅适用于闭合回路中各电压之间的约束关系。

（错）10．当电桥电路中对臂电阻的乘积相等时，则该电桥电路的桥支路上电流必为零。

亲爱的朋友，很高兴能在此相遇！欢迎您阅读文档电路习题集及答案，这篇文档是由我们精心收集整理的新文档。

相信您通过阅读这篇文档，一定会有所收获。

假若亲能将此文档收藏或者转发，将是我们莫大的荣幸，更是我们继续前行的动力。

电路习题集及答案篇一：电路习题及答案第一章电路的基本概念和基本定律1.1指出图（a）、（b）两电路各有几个节点？几条支路？几个回路？几个网孔？(a)(b)习题1.1电路1.2标出图示电路中，电流、电动势和电压的实际方向，并判断A、B、C三点电位的高低。

1.3如图所示电路，根据以下各种情况，判断A、C两点电位的高低。

（1）用导线连接B、C；（2）B、D两点接地；（3）两电路无任何电气联系。

习题1.2电路习题1.3电路1.4有人说，“电路中，没有电压的地方就没有电流，没有电流的地方也就没有电压”。

这句话对吗？为什么？1.5求图示电路中，A点的电位。

（a）（b）习题1.5电路1.6如图所示电路，求开关闭合前、后，UAB和UCD的大小。

习题1.6电路习题1.7电路1.7求图示电路中，开关闭合前、后A点的电位。

1.8如图所示电路，求开关闭合前及闭合后的UAB、电流I1、I2和I3的大小。

习题1.8电路习题1.9电路1.9如图所示电路，电流和电压参考方向如图所示。

求下列各种情况下的功率，并说明功率的流向。

（1）i2A,u100V，（2）i5A,u120V，（3）i3A,u80V，（4）i10A,u60V1.10一盏220V/40W的日光灯，每天点亮5小时，问每月（按30天计算）消耗多少度电？若每度电费为0.45元，问每月需付电费多少元？1.11求如图所示电路中,A、B、C、D元件的功率。

问哪个元件为电源？哪个元件为负载？哪个元件在吸收功率？哪个元件在产生功率？电路是否满足功率平衡条件？（已知UA30V,UB10V,UCUD40V，I15A,I23A,I32A。

）习题1.11电路1.12已知一电烙铁铭牌上标出“25W，220V”。

第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念，电路等效变换的方法是电路问题分析中经常使用的方法。

所谓两个电路是互为等效的，是指（1）两个结构参数不同的电路再端子上有相同的电压、电流关系，因而可以互相代换；（2）代换的效果是不改变外电路（或电路中未被代换的部分）中的电压、电流和功率。

由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。

等效的对象是外接电路（或电路未变化部分）中的电压、电流和功率。

等效变换的目的是简化电路，方便地求出需要求的结果。

深刻地理解“等效变换”的思想，熟练掌握“等效变换”的方法在电路分析中是重要的。

2-1 电路如图所示，已知12100,2,8s u V R k R k ==Ω=Ω。

若：（1）38R k =Ω；（2）处开路）33(R R ∞=；（3）处短路）33(0R R =。

试求以上3种情况下电压2u 和电流23,i i 。

解：（1）2R 和3R 为并联，其等效电阻84R k ==Ω，则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==（2）当∞=3R ，有03=imA u i s 10100212===V i R u 80108222=⨯==（3）03=R ，有0,022==u imA R u i s 50210013===2-2 电路如图所示，其中电阻、电压源和电流源均为已知，且为正值。

求：（1）电压2u 和电流2i ；（2）若电阻1R 增大，对哪些元件的电压、电流有影响？影响如何？解：（1）对于2R 和3R 来说，其余部分的电路可以用电流源s i 等效代换，如题解图（a ）所示。

因此有 32332R R i R i += 32322R R i R R u s+=（2）由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源，如题解图（b ）所示。

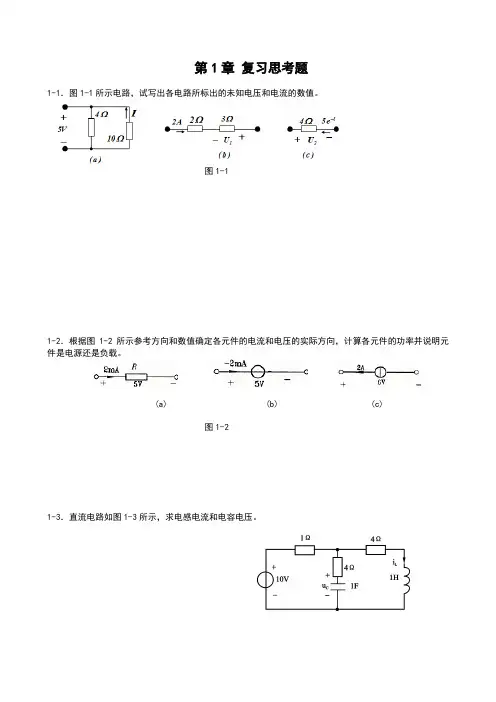
第1章复习思考题1-1．图1-1所示电路，试写出各电路所标出的未知电压和电流的数值。

图1-11-2．根据图1-2所示参考方向和数值确定各元件的电流和电压的实际方向，计算各元件的功率并说明元件是电源还是负载。

(a) (b) (c)图1-21-3．直流电路如图1-3所示，求电感电流和电容电压。

图1-31-4．如图1-4所示，电路中包含的各个元件的电压和电流参考方向如图所示，其中100P 1=W ，10P 2-=W ，50P 3=W ，20P 4=W ，求5P ，元件5是电源还是负载？图1-41-5．求图1-5所示电路中的电压1u 和1i 。

图1-51-6．求图1-6所示电路中的电压u 。

3Ω2Ω4Ωi10 V图1-61-7．求图1-7所示电路中的电压U 。

2ΩU4Ω+ -+ -+- +- 5V2V 5V 1Aa bde图1-71-8．图1-8所示电路中，已知5u ab -=V ，求电压源电压s u 。

图1-81-9．电路如图1-9所示，试求电压U X 。

图1-91-10．如图1-10所示的图，如果选1、2、3、4、8支路为树，则其基本回路组是什么？如果选择自然网孔为基本回路组，则其对应的树由哪些支路组成？②⑤1 2 3 4610 ④89 ⑥57 ③图1-10第2章复习思考题2-1．写出题2 1图所示各电路的端口电压电流的伏安特性方程。

(a) (b)图2-12-2．电路如图2-2(a)、(b)、(c)、(d)、(e)和(f)所示，试计算a、b两端的电阻，其中电阻R=8。

(a) (b)(c)(d)(e) (f)图2-22-3． 利用电源等效变换，化简图2-3(a)和(b)的一端口网络。

(a) (b)图2-32-4．利用电源的等效变换求图示2-4电路中的电流I 。

图2-42Ω6V+I2Ω 2A7Ω6A2Ω2-5．求图2-5电路中的受控电流源的功率。

图2-5 2-6．求图2-6各电路的输入电阻R in。

图2-6第3章复习思考题3-1．用支路电流法求图3-1所示电路中各支路电流及各电阻上吸收的功率。

第2章 整流电路2. 2图2-8为具有变压器中心抽头的单相全波可控整流电路,问该变压器还有直流磁化问题吗?试说明:晶闸管承受的最大反向电压为22U 2;当负载是电阻或电感时，其输出电压和电流的波形与单相全控桥时一样。

答：具有变压器中心抽头的单相全波可控整流电路，该变压器没有直流磁化问题。

因为单相全波可控整流电路变压器二次侧绕组中，在正负半周上下绕组中的电流方向相反，波形对称，其一个周期内的平均电流为零，故不存在直流磁化的问题。

以下分析晶闸管承受最大反向电压及输出电压和电流波形的情况。

①以晶闸管VT2为例。

当VT1导通时，晶闸管VT2通过VT1与2个变压器二次绕组并联，所以VT2承受的最大电压为22U 2。

②当单相全波整流电路与单相全控桥式整流电路的触发角α一样时，对于电阻负载：(O~α)期间无晶闸管导通，输出电压为0；(α~π)期间,单相全波电路中VT1导通，单相全控桥电路中VTl 、VT4导通，输出电压均与电源电压U 2相等；( π~απ+)期间均无晶闸管导通，输出电压为0；(απ+~2π)期间，单相全波电路中VT2导通，单相全控桥电路中VT2、VT3导通，输出电压等于－U 2。

对于电感负载： ( α~απ+)期间，单相全波电路中VTl 导通，单相全控桥电路中VTl 、VT4导通，输出电压均与电源电压U2相等； (απ+~2απ+)期间，单相全波电路中VT2导通，单相全控桥电路中VT2、VT3导通，输出波形等于-U2。

可见，两者的输出电压一样，加到同样的负载上时，那么输出电流也一样。

2.3.单相桥式全控整流电路，U 2=100V ，负载中R=20Ω，L 值极大，当α=︒30时，要求：①作出U d 、I d 、和I 2的波形；②求整流输出平均电压U d 、电流I d ，变压器二次电流有效值I 2；③考虑平安裕量，确定晶闸管的额定电压和额定电流。

解：①Ud 、Id、和I2的波形如以下图：②输出平均电压Ud 、电流Id、变压器二次电流有效值I2分别为：Ud =0.9U2cosα=0.9×100×cos︒30＝77.97〔V〕Id＝Ud/R=77.97/2=38.99(A)I2=Id=38.99(A)③晶闸管承受的最大反向电压为：2U2=1002=141.4(V) -考虑平安裕量，晶闸管的额定电压为：UN=(2~3)×141.4=283~424(V)详细数值可按晶闸管产品系列参数选取。

第7节闭合电路的欧姆定律1．了解内电路、外电路，知道电动势等于内外电路电势降落之和。

2．掌握闭合电路的欧姆定律并会进行有关计算。

3．会用闭合电路的欧姆定律分析路端电压与负载的关系。

一、闭合电路的欧姆定律1．闭合电路的组成及电流流向2．闭合电路的欧姆定律二、路端电压与负载(外电阻)的关系1．路端电压与电流的关系：U＝□01E－Ir。

2．路端电压随外电阻的变化规律(1)外电阻R增大时，电流I□02减小，外电压U□03增大，当R增大到无限大(断路)时，I ＝□040，U＝□05E，即断路时的□06路端电压等于电源□07电动势。

(2)外电阻R减小时，电流I□08增大，路端电压U□09减小，当R减小到零时，即电源短路时I ＝□10E r，U ＝□110。

在实验课上，小明同学用电压表去测量1节新干电池的电动势约为1.5 V,1节旧干电池的电动势约为1.45 V ，现在他把这样的两节旧电池串联后接在一个标有“3 V 2 W”的小灯泡两端，结果发现小灯泡不发光，检查电路的连接，各处均无故障。

电池虽然旧了，但电动势并没有减小多少，那么小灯泡为什么不亮呢？提示：电池变旧后，电动势并不明显减小，但内阻明显变大，因而使电路中的电流很小，小灯泡不发光。

(1)电动势就是电源两极间的电压。

( )(2)闭合电路中的电流跟电源电动势成正比，跟整个电路的电阻成反比。

( ) (3)外电路的电阻越大，路端电压就越大。

( ) (4)闭合电路中的短路电流无限大。

( )(5)电源断路时，电流为零，所以路端电压也为零。

( )(6)外电阻变化可以引起内电压的变化，从而引起内电阻的变化。

( ) (7)电源U ­I 图象上某点纵、横坐标的乘积对应此时的输出功率。

( ) 提示：(1)× (2)√ (3)√ (4)× (5)× (6)× (7)√课堂任务闭合电路的欧姆定律仔细观察下列图片，认真参与“师生互动”。

电路理论练习参考解答§3、线性电阻电路1）、对第一小节中的电路，假定g1=g2=…=g10=1s，求节点1、3与地之间形成的二端口(不包括图中的电流源)的开路阻抗矩阵。

解：将各g 的值代入节点电压方程，先在节点1注入单位电流源，有：[]100000Tn n Y V ⋅=其中210100021100012001100310100031001013n Y −−⎡⎤⎢⎥−−⎢⎥⎢⎥−−=⎢⎥−−⎢⎥⎢⎥−−⎢⎥−−⎣⎦解出上述方程，得[0.8833 0.3500 0.2833 0.4167 0.3667 0.2167]n V =T ， 因此0.8833，0.2833。

再在节点3注入单位电流源，节点电压方程成为：11z =21z =[]001000Tn n Y V ⋅=解[0.45 0.65 1.05 0.25 0.30 0.45]n V =T 故0.45， 1.05，从而12z =22z =0.88330.28330.451.05oc Z ⎡⎤=⎢⎥⎣⎦2）、试推导二端口从y 参数到传输参数的转换式。

解：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−Δ−−−=⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡⇒⎥⎦⎤⎢⎣⎡−⎥⎦⎤⎢⎣⎡−=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡−⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−⎥⎦⎤⎢⎣⎡−⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡−⎥⎦⎤⎢⎣⎡−⇒⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡−21112121212222221212111112222121121112211222112112121222112112122211211211100110010100101001y y y y y y y i v y y y y i v i v y y i v y y i v i v y y y y i i v v y y y y v v y y y y i i ；即得传输参数表达，其中，11221221y y y y y Δ=−。

第2章 线性直流电路2.1. 求图示电路的a b 端口的等效电阻。

图 题 2.1解：根据电桥平衡有eq (2060)||(2060)40R =++=Ω2.2．图中各电阻均为6Ω，求电路的a b 端口的等效电阻。

abab图 题 2.2解：根据电桥平衡，去掉电桥电阻有eq [(66)||(66)6]||64R =+++=Ω2.3求图示电路的电压1U 及电流2I 。

20k Ω1U +-图 题2.220k Ω(b)+_U解：电路等效如图(b)所示。

图中等效电阻 (13)520(13)k //5k k k 1359R +⨯=+ΩΩ=Ω=Ω++由分流公式得：220mA 2mA 20k RI R =⨯=+Ω电压220k 40V U I =Ω⨯=再对图(a)使用分压公式得：13==30V 1+3U U ⨯2.4 图示电路中要求21/0.05U U =，等效电阻eq 40k R =Ω。

求1R 和2R 的值。

2U +-1U 图 题2.3_1R U解：设2R 与5k Ω的并联等效电阻为2325k 5k R R R ⨯Ω=+Ω(1)由已知条件得如下联立方程：32113130.05(2) 40k (3)eqR U U R R R R R ⎧==⎪+⎨⎪=+=Ω⎩由方程(2)、(3)解得138k R =Ω 32k R =Ω再将3R 代入(1)式得 210k 3R =Ω 2.5求图示电路的电流I 。

图 题 2.5解：由并联电路分流公式，得1820mA 8mA (128)I Ω=⨯=+Ω2620mA 12mA (46)I Ω=⨯=+Ω由节点①的KCL 得128mA 12mA 4mA I I I =-=-=- 2.6求图示电路的电压U 。

图 题2.5120Ω(a)(b)解：首先将电路化简成图(b)。

图中1(140100)240R =+Ω=Ω2(200160)120270360(200160)120R ⎡⎤+⨯=+Ω=Ω⎢⎥++⎣⎦由并联电路分流公式得211210A 6A R I R R =⨯=+及 21104A I I =-= 再由图(a)得321201A 360120I I =⨯=+由KVL 得，3131200100400V U U U I I =-=-=- 2.7求图示电路的等效电阻x R 。

西安交通大学 面朝大海目 录附录一：电路试卷 ........................................................ 38 附录二：习题集部分答案 (58)第一章 电路模型和电路定律一、是非题 (注:请在每小题后[ ]内用"√"表示对,用"×"表示错).1. 电路理论分析的对象是电路模型而不是实际电路。

[ ] .2. 欧姆定律可表示成 u R i =?, 也可表示成u R i =-?,这与采用的参考方向有关。

[ ].3. 在节点处各支路电流的方向不能均设为流向节点，否则将只有流入节点的电流而无流出节点的电流。

[ ] .4. 在电压近似不变的供电系统中，负载增加相当于负载电阻减少。

[ ] .5.理想电压源的端电压是由它本身确定的，与外电路无关，因此流过它的电流则是一定的，也与外电路无关。

[ ] .6. 电压源在电路中一定是发出功率的。

[ ] .7. 理想电流源中的电流是由它本身确定的，与外电路无关。

因此它的端电压则是一定的，也与外电路无关。

[ ] .8. 理想电流源的端电压为零。

[ ] .9. 若某元件的伏安关系为u ＝2i+4，则该元件为线性元件。

[ ] .10. 一个二端元件的伏安关系完全是由它本身所确定的，与它所接的外电路毫无关系。

[ ] .11.元件短路时的电压为零,其中电流不一定为零。

元件开路时电流为零,其端电压不一定为零。

[ ] .12. 判别一个元件是负载还是电源，是根据该元件上的电压实际极性和电流的实际方向是否一致（电流从正极流向负极）。

当电压实际极性和电流的实际方向一致时，该元件是负载，在吸收功率；当电压实际极性和电流的实际方向相反时，该元件是电源（含负电阻），在发出功率 [ ].13.在计算电路的功率时，根据电压、电流的参考方向可选用相应的公式计算功率。

若选用的公式不同,其结果有时为吸收功率，有时为产生功率。

第二章 正弦交流电路2.1 基本要求(1) 深入理解正弦量的特征，特别是有效值、初相位和相位差。

(2) 掌握正弦量的各种表示方法及相互关系。

(3) 掌握正弦交流电路的电压电流关系及复数形式。

(4) 掌握三种单一参数（R ，L ，C ）的电压、电流及功率关系。

(5) 能够分析计算一般的单相交流电路，熟练运用相量图和复数法。

(6) 深刻认识提高功率因数的重要性。

(7) 了解交流电路的频率特性和谐振电路。

2.2 基本内容 2.2.1 基本概念 1. 正弦量的三要素(1) 幅值（U m ，E m ，I m ）、瞬时值（u, e, i ）、有效值（U ，E ，I ）。

注：有效值与幅值的关系为：有效值2幅值=。

(2) 频率（f ）、角频率（ω）、周期（T ）。

注：三者的关系是 Tf ππω22==。

(3) 相位（ϕω+t ）、初相角（ϕ）、相位差（21ϕϕ-）。

注：相位差是同频率正弦量的相位之差。

2. 正弦量的表示方法 (1) 函数式表示法：。

)sin();sin();sin(i m e m u m t I i t E e t U u ϕωϕωϕω-=+=+= (2) 波形表示法：例如u 的波形如图2-1-1(a)所示。

(3) 相量（图）表示法：使相量的长度等于正弦量的幅值（或有效值）； 使相量和横轴正方向的夹角等于正弦量的初相角； 使相量旋转的角速度等于正弦量的角速度。

注：例。

)60sin(24,)30sin(2621V t u V t u o o +=+=ωω求?21=+u u解：因为同频率同性质的正弦量相加后仍为正弦量，故)sin(221ϕω+==+t U u u u , 只要求出U 及ϕ问题就解决了。

解1：相量图法求解如下：具体步骤为三步法（如图2-1-2所示）：第一步：画出正弦量u 1、u 2的相量12U U 、（U 1=6，U 2=4）。

第二步：在相量图上进行相量的加法，得到一个新相量U。