3.5 直线和圆的位置关系(2)切线判定定理

学习笔记-点和圆、直线和圆的位置关系主要内容：点和圆的位置关系、直线和圆的位置关系、切线的判定及性质、圆和圆的位置关系。

（1）点和圆的位置关系：数量关系和位置关系的对应（2）圆的确定1、过一点可做无数个圆；2、过二点可做无数个圆；3、不在同一条直线上的三点确定（有且只有）一个圆；过在一条直线的三点不能做圆；4、不在同一条直线上的四点有可能作一个圆，也有可能做不出一个圆；（3）三角形的外接圆1、三角形外接圆、圆的内接三角形、外心（外接圆圆心，三角形三条边的中垂线交点）；2、“接”：三角形顶点与圆的关系，顶点在圆上；“外、内”：三角形和圆的位置关系；（4）反证法1、定义：假设命题的结论不成立，由此经过推理得出矛盾，有矛盾断定假设不正确，从而得出原命题成立；2、使用场景：用于解决不易直接证明或不能直接证明的命题，主要适用于：①结论是否定形式的命题②结论是无限形式的命题③结论是“至多”或“至少”形式的命题3、否定形式“大（小）于——不大（小）于”“或——且”“至多有n个——至少有n+1个”“都是——不都是”（5）“一箭穿心”模型（圆外一点到圆的最大距离和最小距离）先把圆心到点的距离d求出来，最大距离为d+r，最小距离为d-r（三角形三边关系可证明）；（1）直线和圆的位置关系：数量关系和位置关系的对应（2）直线与圆相离，直线到圆的最大距离和最小距离先把圆心到直线的距离d求出来，最大距离为d+r，最小距离为d-r（垂线段最短可证明）；（1）切线的定义➢与圆只有一个交点的直线➢圆心到直线的距离等于半径的直线（2）切线的判定➢定义法：与圆只有一个公共点➢数量关系：d=r（圆心到直线的距离等于半径）➢位置关系（切线判定定理）：经过半径的外端并且垂直于这条半径的直线是圆的切线证明切线的常用辅助线：◆有交点，连半径，证垂直◆无交点，作垂直，证半径（3）切线的性质➢切线与圆有且只有一个公共点➢圆心到切线的距离等于圆的半径➢（切线的性质定理）圆的切线垂直于过切点的半径以下是两个推论：⏹经过圆心且垂直于切线的直线必经过切点⏹经过切点且垂直于切线的直线必经过圆心有切线后的常用辅助线：切点的位置确定：连接圆心和切点，得垂直，即连切点得垂直切点位置不确定：过圆心作切线的垂线，垂足就是切点，即作垂直得切点（4）切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角主要讲解下面这个图形：找出图中互相垂直的线段、直角三角形、等腰三角形、全等三角形注意：适当讲解弦切角定理（两角互余可证明），开阔学生做题的思路。

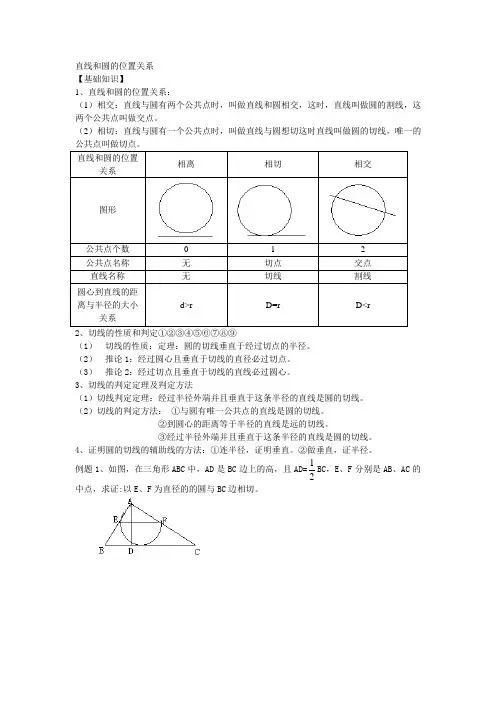
直线和圆的位置关系 【基础知识】1、直线和圆的位置关系：（1）相交：直线与圆有两个公共点时，叫做直线和圆相交，这时，直线叫做圆的割线，这两个公共点叫做交点。

（2）相切：直线与圆有一个公共点时，叫做直线与圆想切这时直线叫做圆的切线，唯一的（1） 切线的性质：定理：圆的切线垂直于经过切点的半径。

（2） 推论1：经过圆心且垂直于切线的直径必过切点。

（3） 推论2：经过切点且垂直于切线的直线必过圆心。

3、切线的判定定理及判定方法（1）切线判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线。

（2）切线的判定方法： ①与圆有唯一公共点的直线是圆的切线。

②到圆心的距离等于半径的直线是远的切线。

③经过半径外端并且垂直于这条半径的直线是圆的切线。

4、证明圆的切线的辅助线的方法：①连半径，证明垂直。

②做垂直，证半径。

例题1、如图，在三角形ABC 中，AD 是BC 边上的高，且AD=21BC ，E 、F 分别是AB 、AC 的中点，求证:以E 、F 为直径的的圆与BC 边相切。

【跟踪练习】1、已知：如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE，求证：DE与半圆O相切．2、如图，已知CD是△ABC中AB边上的高，以CD为直径的⊙O交CA于点E，点G是AD的中点．求证：GE是⊙O的切线；5、三角形的内切圆（1）内切圆：和三角形三边都相切的圆叫做三角形的内切圆。

内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心，这个三角形叫做圆的外接三角形。

三角形的内心到三边的距离相等。

例题2．如图，在△ABC中，AB=AC，内切圆O与边BC，AC，AB分别切于D，E，F．（1）求证：BF=CE；（2）若∠C=30°，AC的长．例题3、如图，⊙I切△ABC的边分别为D，E，F，∠B=70°，∠C=60°，M是 DEF上的动点（与D，E不重合），∠DMF的大小一定吗？若一定，求出∠DMF的大小；若不一定，请说明理由．【跟踪练习】1．图1，⊙O内切于△ABC，切点为D，E，F．已知∠B=50°，∠C=60°，•连结OE，OF，DE，DF，那么∠EDF等于（）A．40°B．55°C．65°D．70°图1 图2 图32．如图2，⊙O是△ABC的内切圆，D，E，F是切点，∠A=50°，∠C=60°，•则∠DOE=（）A．70°B．110°C．120°D．130°3．如图3，△ABC中，∠A=45°，I是内心，则∠BIC=（）A．112.5°B．112°C．125°D．55°6、切线长定理及切线长概念（1）切线长的概念：在经过员外一点的圆的切线上，这点和切点之间的线段的长，叫做这点倒圆的切线长。

直线与圆的位置关系及切线的性质与判定【知识点一】：直线与圆的位置关系（1）直线和圆的三种位置关系：①相离：一条直线和圆没有公共点．②相切：一条直线和圆只有一个公共点，叫做这条直线和圆相切，这条直线叫圆的切线，唯一的公共点叫切点．③相交：一条直线和圆有两个公共点，此时叫做这条直线和圆相交，这条直线叫圆的割线．（2）判断直线和圆的位置关系：设⊙O的半径为r，圆心O到直线l的距离为d．①直线l和⊙O相交⇔d＜r②直线l和⊙O相切⇔d＝r③直线l和⊙O相离⇔d＞r．【典例分析】1．如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是（）A．8≤AB≤10B．8＜AB≤10C．4≤AB≤5D．4＜AB≤52．如图，在平面直角坐标系中，x轴上一点A从点（﹣3，0）出发沿x轴向右平移，当以A为圆心，半径为1的圆与函数y＝x的图象相切时，点A的坐标变为（）A．（﹣2，0）B．（﹣，0）或（，0）C．（﹣，0）D．（﹣2，0）或（2，0）3．如图，∠ABC＝80°，O为射线BC上一点，以点O为圆心，OB长为半径作⊙O，要使射线BA与⊙O相切，应将射线BA绕点B按顺时针方向旋转（）A．40°或80°B．50°或100°C．50°或110°D．60°或120°第1题图第2题图第3题图4．如图，在平面直角坐标系中，已知⊙O的半径为2，动直线AB与x轴交于点P（x，0），直线AB与x轴正方向夹角为45°，若直线AB与⊙O有公共点，则x的取值范围是（）A．﹣2≤x≤2B．﹣2＜x＜2C．0≤x≤2D．﹣2≤x≤25．如图，已知⊙P的半径为2，圆心P在抛物线y＝x2﹣1上运动，当⊙P与x轴相切时，圆心P的坐标为．6．如图，半圆的圆心与坐标原点重合，半圆的半径1，直线l的解析式为y＝x+t．若直线l与半圆只有一个交点，则t的取值范围是．第4题图第5题图第6题图7．如图Rt△ABC中，∠ABC＝90°，P是斜边AC上一个动点，以BP为直径作⊙O交BC于点D，与AC的另一个交点E，且＝，连接DE．（1）若＝140°，求∠C的度数．（2）求证AB＝AP．8．如图，在△ABC中，∠C＝90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．（1）判断直线DE与⊙O的位置关系，并说明理由；（2）若AC＝6，BC＝8，OA＝2，求线段DE的长．【知识点二】：切线的性质（1）切线的性质①圆的切线垂直于经过切点的半径．②经过圆心且垂直于切线的直线必经过切点．③经过切点且垂直于切线的直线必经过圆心．（2）切线的性质可总结如下：如果一条直线符合下列三个条件中的任意两个，那么它一定满足第三个条件，这三个条件是：①直线过圆心；②直线过切点；③直线与圆的切线垂直．（3）切线性质的运用运用切线的性质进行计算或证明时，常常作的辅助线是连接圆心和切点，通过构造直角三角形或相似三角形解决问题．【典例分析】1．如图，AB，BC，CD分别与⊙O相切于E、F、G三点，且AB∥CD，BO＝3，CO＝4，则OF的长为（）A．B．C．D．52．AB为⊙O的直径，延长AB到点P，过点P作⊙O的切线，切点为C，连接AC，∠P＝40°，D为圆上一点，则∠D的度数为（）A．25°B．30°C．35°D．40°3．如图，菱形OABC的顶点A，B，C在⊙O上，过点B作⊙O的切线交OA的延长线于点D．若⊙O的半径为1，则BD的长为（）A．1B．2C．D．第1题图第2题图第3题图4．如图，AB是⊙O的直径，C，D是⊙O上两点，AD＝CD，过点C作⊙O的切线交AB的延长线于点E，若∠E ＝50°，则∠ACD等于（）A．40°B．50°C．55°D．60°5．如图，在平面直角坐标系中，点P在第一象限，⊙P与x轴、y轴都相切，且经过矩形AOBC的顶点C，与BC 相交于点D．若⊙P的半径为5，点A的坐标是（0，8）．则点D的坐标是（）A．（9，2）B．（9，3）C．（10，2）D．（10，3）6．如图，已知一次函数y＝﹣x+2的图象与坐标轴分别交于A、B两点，⊙O的半径为1，P是线段AB上的一个点，过点P作⊙O的切线PM，切点为M，则PM的最小值为（）A．2B．C．D．第4题图第5题图第6题图7．如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连接PM，以点P为圆心，PM长为半径作⊙P．当⊙P与正方形ABCD的边相切时，BP的长为．8．如图，▱ABCD的两边AB、BC分别切⊙O于点A、C，若∠B＝50°，则∠DAE＝．第7题图第8题图9．如图，以BC为直径的⊙O交△ABC的边AB于点D，过点D作⊙O的切线交AC于点E，且AC＝BC．（1）求证：DE⊥AC；（2）若BC＝4cm，AD＝3cm，求AE的长．10．如图，AB为⊙O的直径，点C在⊙O上，AD与过点C的切线互相垂直，垂足为D．连接BC并延长，交AD 的延长线于点E．（1）求证：AE＝AB；（2）若AB＝20，BC＝16，求CD的长．11．如图，AB为⊙O的直径，点C是⊙O上一点，CD与⊙O相切于点C，过点A作AD⊥DC，连接AC，BC．（1）求证：AC是∠DAB的角平分线；（2）若AD＝2，AB＝3，求AC的长．12．如图，在Rt△ABC中，∠C＝90°，以BC为直径的⊙O交AB于点D，切线DE交AC于点E．（1）求证：∠A＝∠ADE；（2）若AD＝8，DE＝5，求BC的长．13．已知直线l与⊙O相切，AB是⊙O的直径，AD⊥l于点D．（1）如图①，当直线l与⊙O相切于点C时，若∠DAC＝30°，求∠BAC的大小；（2）如图②，当直线l与⊙O相交于点E，F时，若∠DAE＝18°，求∠BAF的大小．【知识点三】：切线的判定（1）切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．（2）在应用判定定理时注意：①切线必须满足两个条件：a、经过半径的外端；b、垂直于这条半径，否则就不是圆的切线．②切线的判定定理实际上是从”圆心到直线的距离等于半径时，直线和圆相切“这个结论直接得出来的．③在判定一条直线为圆的切线时，当已知条件中未明确指出直线和圆是否有公共点时，常过圆心作该直线的垂线段，证明该线段的长等于半径，可简单的说成“无交点，作垂线段，证半径”；当已知条件中明确指出直线与圆有公共点时，常连接过该公共点的半径，证明该半径垂直于这条直线，可简单地说成“有交点，作半径，证垂直”．【典例分析】1．如图，AB为⊙O的直径，AC平分∠BAD交⊙O于点C，CD⊥AD，垂足为点D．求证：CD是⊙O的切线．2．如图，在Rt△ABC中，∠BAC＝90°，BD是角平分线，以点D为圆心，DA为半径的⊙D与AC相交于点E （1）求证：BC是⊙D的切线；（2）若AB＝5，BC＝13，求CE的长．3．如图，四边形ABCD中，AB＝AD＝CD，以AB为直径的⊙O经过点C，连接AC、OD交于点E．（1）求证：OD∥BC；（2）若AC＝2BC，求证：DA与⊙O相切．4．已知：AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使AB＝AC，连接AC，过点D作DE⊥AC，垂足为E．（1）求证：DC＝BD；（2）求证：DE为⊙O的切线．5．如图，AB是⊙O的直径，点P在AB的延长线上，弦CD⊥AB，联结OD、PC，∠ODC＝∠P，求证：PC是⊙O的切线．6．如图，在Rt△ABC中，∠ABC＝90°，∠ACB的平分线CO交AB边于点O，以点O为圆心，OB为半径作⊙O．（1）请判断AC与⊙O的位置关系，并证明你的结论；（2）若BO＝1，∠BAC＝30°，求△AOC的面积．7．如图，在△ABC中，∠C＝90°，AD是∠BAC的平分线，O是AB上一点，以OA为半径的⊙O经过点D．（1）求证：BC是⊙O切线；（2）若BD＝5，DC＝3，求AC的长．8．已知如图，以Rt△ABC的AC边为直径作⊙O交斜边AB于点E，连接EO并延长交BC的延长线于点D，点F 为BC的中点，连接EF．（1）求证：EF是⊙O的切线；（2）若⊙O的半径为3，∠EAC＝60°，求AD的长．。

直线与圆的位置关系【学习目标】1.理解并掌握直线与圆的三种位置关系；2.理解切线的判定定理和性质定理.【要点梳理】要点一、直线与圆的位置关系1.切线的定义：直线与圆有唯一的公共点时，这条直线叫做圆的切线，这个唯一的公共点叫做切点.此时直线与圆的位置关系称为相切.2．直线和圆的三种位置关系：(1) 相交：当直线与圆有两个公共点时，叫做直线与圆相交．(2) 相切：当直线与圆有唯一公共点时，叫做直线与圆相切．这条直线叫做圆的切线，公共点叫做切点．(3) 相离：当直线与圆没有公共点时，叫做直线与圆相离．3．直线与圆的位置关系的判定和性质．直线与圆的位置关系能否像点与圆的位置关系一样通过一些条件来进行分析判断呢？由于圆心确定圆的位置，半径确定圆的大小，因此研究直线和圆的位置关系，就可以转化为直线和点(圆心)的位置关系．下面图(1)中直线与圆心的距离小于半径；图(2)中直线与圆心的距离等于半径；图(3)中直线与圆心的距离大于半径．一般地，直线与圆的位置关系有以下定理：如果⊙O的半径为r，圆心O到直线l的距离为d，那么，（1）d＜r直线l与⊙O相交；（2）d=r直线l与⊙O相切；（3）d＞r直线l与⊙O相离.要点进阶：这三个命题从左边到右边反映了直线与圆的位置关系所具有的性质；从右边到左边则是直线与圆的位置关系的判定．要点二、切线的性质定理和判定定理1．切线的性质定理：圆的切线垂直于过切点的半径.要点进阶：切线的性质定理中要注意：圆的切线是与过切点的半径垂直，不是与任意半径都垂直.2．切线的判定定理：过半径外端且垂直于半径的直线是圆的切线.要点进阶：切线的判定定理中强调两点：一是直线与圆有一个交点，二是直线与过交点的半径垂直，缺一不可. 要点三、三角形的内切圆1．三角形的内切圆：与三角形各边都相切的圆叫做三角形的内切圆.2．三角形的内心：三角形内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心. 三角形的内心到三边的距离都相等.要点进阶：(1) 任何一个三角形都有且只有一个内切圆，但任意一个圆都有无数个外切三角形；(2) 解决三角形内心的有关问题时，面积法是常用的，即三角形的面积等于周长与内切圆半径乘积的一半，即(S为三角形的面积，P为三角形的周长，r为内切圆的半径).【典型例题】类型一、直线与圆的位置关系例1．在Rt△ABC中，∠C=90°，AC=3厘米，BC=4厘米，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？(1)r=2厘米； (2)r=2.4厘米； (3)r=3厘米举一反三：【变式】已知⊙O的半径为10cm，如果一条直线和圆心O的距离为10cm，那么这条直线和这个圆的位置关系为（）A. 相离B. 相切C. 相交D. 相交或相离类型二、切线的判定与性质例2．如图所示，在Rt△ABC中，∠B＝90°，∠A的平分线交BC于D，以D为圆心，DB长为半径作⊙D．求证：AC是⊙D的切线．例3.如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．（1）求BC的长；（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．例4．如图，AB为⊙O的直径，AC为⊙O的弦，AD平分∠BAC，交⊙O于点D，DE⊥AC，交AC的延长线于点E．（1）判断直线DE与⊙O的位置关系，并说明理由；（2）若AE＝8，⊙O的半径为5，求DE的长．O C B A举一反三：【变式1】如图，在△ABC 中，∠CAB=90°，∠CBA=50°，以AB 为直径作⊙O 交BC 于点D ，点E 在边AC 上，且满足ED=EA ． （1）求∠DOA 的度数；（2）求证：直线ED 与⊙O 相切．举一反三：【变式2】如图所示，在△ABC 中，AB ＝BC ＝2，以AB 为直径的⊙O 与BC 相切于点B ，则AC 等于( )A ．2B ．3C ．22D ．23类型三、三角形的内切圆例5．如图，已知O 是△ABC 的内心，∠A=50°，求∠BOC 的度数.O C BA【变式】如图，△ABC 中，∠C=90°，BC=4，AC=3，⊙O 内切与△ABC ，则△ABC 去除⊙O 剩余阴影部分的面积为（ ）A.12-πB. 12-2πC. 14-4πD. 6-π【巩固练习】一、选择题1.已知：如图，PA ，PB 分别与⊙O 相切于A ，B 点，C 为⊙O 上一点，∠ACB=65°，则∠APB 等于( ) A ．65° B ．50° C ．45° D ．40°2．如图，AB 是⊙O 的直径，直线EC 切⊙O 于B 点，若∠DBC=α，则( ) A ．∠A=α B ．∠A=90°－α C ．∠ABD=α D ．∠α2190o-=ABD第1题图 第2题图3．设⊙O 的半径为3，点O 到直线l 的距离为d ，若直线l 与⊙O 至少有一个公共点，则d 应满足的条件是( )A.d=3B. d ＜3C. d≤3D.d＞34.如图，在⊙O 的内接四边形ABCD 中，AB 是直径，∠BCD=120°，过D 点的切线PD 与直线AB 交于点P ，则∠ADP 的度数为（ ）A ．40°B ． 35°C ． 30°D ． 45°5．如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ，且CO ＝CD ，则∠PCA＝（ ） A.30° B.45° C.60° D.67.5°6．已知AB是⊙O的直径，点P是AB延长线上的一个动点，过P作⊙O的切线，切点为C，∠APC的平分线交AC于点D，则∠CDP等于（）A.30°B.60°C.45°D.50°二、填空题7．如图，AB是⊙O的直径，BC切⊙O于点B，AC交⊙O于点D.若AC=5，BC=3，则⊙O的半径为_______.8．如图，⊙O的切线PC交直径AB的延长线于点P，C为切点.若∠P=30°，⊙O的半径为1，则PB的长为______________.9．在△ABO中，OA=OB=2cm，⊙O的半径为1cm，当∠ABO=时，直线AB与⊙O相切．10.如图所示，已知直线AB是⊙O的切线，A为切点，OB交⊙O于点C，点D在⊙O上，且∠OBA＝40°，则∠ADC＝________．OCB A 11．如图所示，已知△ABC ，AC ＝BC ＝6，∠C ＝90°，O 是AB 的中点，⊙O 与AC 、BC 分别相切于点D 与点E ．点F 是⊙O 与AB 的一个交点，连DF 并延长交CB 的延长线于点G ，则CG ＝________．12．木工师傅可以用角尺测量并计算出圆的半径r .用角尺的较短边紧靠O ，并使较长边与O 相切于点C .假设角尺的较长边足够长，角尺的顶点为B ，较短边8cm AB .若读得BC 长为cm a ，则用含a 的代数式表示r 为 .三、解答题13. 如图，已知⊙O 是边长为2的等边△ABC 的内切圆，求⊙O 的面积.14． AB 是⊙O 的直径，BC 切⊙O 于B ，AC 交⊙O 于D 点，过D 作⊙O 的切线DE 交BC 于E.求证：CE=BE.15.如图，AB是⊙O的弦，OC⊥OA，交AB与点P，且PC=BC，求证：BC是⊙O的切线．。

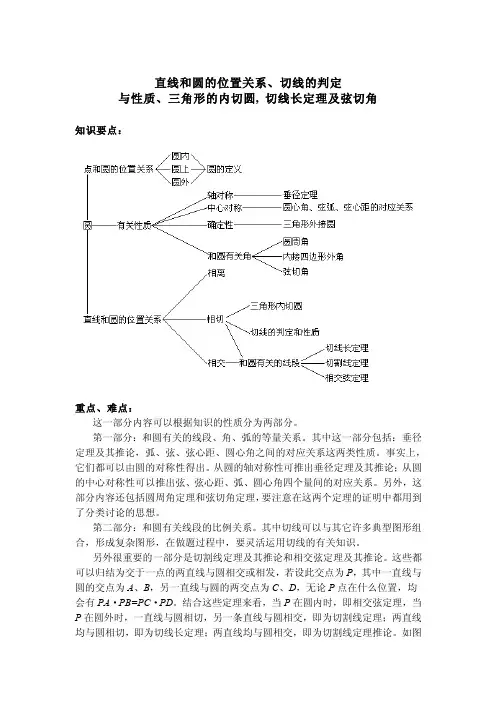
直线和圆的位置关系、切线的判定与性质、三角形的内切圆, 切线长定理及弦切角知识要点：重点、难点：这一部分内容可以根据知识的性质分为两部分。

第一部分：和圆有关的线段、角、弧的等量关系。

其中这一部分包括：垂径定理及其推论，弧、弦、弦心距、圆心角之间的对应关系这两类性质。

事实上，它们都可以由圆的对称性得出。

从圆的轴对称性可推出垂径定理及其推论；从圆的中心对称性可以推出弦、弦心距、弧、圆心角四个量间的对应关系。

另外，这部分内容还包括圆周角定理和弦切角定理，要注意在这两个定理的证明中都用到了分类讨论的思想。

第二部分：和圆有关线段的比例关系。

其中切线可以与其它许多典型图形组合，形成复杂图形，在做题过程中，要灵活运用切线的有关知识。

另外很重要的一部分是切割线定理及其推论和相交弦定理及其推论。

这些都可以归结为交于一点的两直线与圆相交或相发，若设此交点为P，其中一直线与圆的交点为A、B，另一直线与圆的两交点为C、D，无论P点在什么位置，均会有PA·PB=PC·PD。

结合这些定理来看，当P在圆内时，即相交弦定理，当P在圆外时，一直线与圆相切，另一条直线与圆相交，即为切割线定理；两直线均与圆相切，即为切线长定理；两直线均与圆相交，即为切割线定理推论。

如图1—5所示。

相交弦定理相交弦定理推论 切线长定理 PA PB PC PD ··=()PA PB PC PD 22=· PA PB PC PDPA PC··=∴=切割线定理 切割线定理推论 PA PB PC PD ··=PA PB PC PD ··=PA PC PD 2=·基础知识(1)知识内容及要求直线和圆的位置关系是从运动的观点研究的, 相切是位置中的一种特殊情况, 切线的判定和性质定理是研究相切问题的重点, 三角形的内切圆是两个基本图形的组合, 切线长定理是切线的数量的研究, 弦切角又是圆中十分重要的角。

与圆有关的位置关系1、点与圆的位置关系如果圆的半径是r ，这个点到圆心的距离为d ，那么：（1）点在圆外⇔d ＞r ； （2）点在圆上⇔d ＝r ； （3）点在圆内⇔d ＜r ； 2、直线与圆位置关系的定义及有关概念（1）直线与圆有两个公共点，叫做直线与圆相交，这直线叫做圆的割线，公共点叫做交点. （2）直线和圆有一公共点时，叫做直线和圆相切，这直线叫做圆的切线，公共点叫做切点. （3）直线和圆没有公共点时，叫做直线和圆相离. 3、直线和圆的位置关系如果⊙O 的半径为r ，圆心O 到直线l 的距离为d ，那么 （1）直线l 和⊙O 相交⇔d ＜r ； （2）直线l 和⊙O 相切⇔d ＝r ； （3）直线l 和⊙O 相离⇔d ＞r ；典例精析例1：已知直线l ：y ＝x －3和点A （0，3），B （3，0），设P 点为l 上一点，试判断P 、A 、B 是否在同一个圆上？例2：下列说法正确的是（ ）A. 过圆内接三角形的顶点的直线是圆的切线B. 若直线与圆不相切，则它和圆相交C. 若直线和圆有公共点，直线和圆相交D. 若直线和圆有唯一公共点，则公共点是切点例3：设直线l 到⊙O 的圆心的距离为d ，⊙O 的半径为R，并使20x R -+=，试根据关于x 的一元二次方程根的情况讨论l 与⊙O 的位置关系.3、圆和圆的位置关系⎧⎨⎩外离(没有公共点)(1)相离内含(包括同心圆) ()⎧⎨⎩外切(2)相切有一个公共点内切(3)相交(有两个公共点)注：两圆同心是两圆内含的一种特例.2、两圆的位置与两圆的半径、圆心距之间的数量关系 设两圆的半径分别为R 和r ，圆心距为d ，那么 （1）两圆外离⇒d ＞R ＋r （2）两圆外切⇒d ＝R ＋r （3）两圆相交⇒R －r ＜d ＜R +r（4）两圆内切⇒d ＝R －r （5）两圆内含⇒d ＜R －r典例精析例1：已知两个圆的半径分别为2、3，圆心距是d ，若两圆有公共点，则d 的取值范围为______. 例2：已知⊙O 1和⊙O 2内切，圆心距为7cm ，⊙O 1的半径为8cm ，求⊙O 2的半径.DC BA例4：如图：⊙M 的半径为8cm ，⊙N 的半径为6cm ，MN ＝10cm ，两圆相交于A 、B 两点，连接AB 与MN 交于点C ，求AB 的长为多少？与相切有关的性质 定理 1、切线的性质定理：定理：圆的切线垂直于过切点的半径.推论1：经过圆心且垂直于切点的直线必经过切点. 推论2：经过切点且垂直于切点的直线必经过圆心. 2、切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线. 3、切线的判定方法（1）定义：和圆只有一个公共点的直线是圆的切线；（2）数量关系：和圆心的距离等于半径的直线是圆的切线；（证长度） （3）定理：过半径外端且与这条半径垂直的直线是圆的切线.（证角度） 两圆相切与相交的性质：（1）如果两圆相切，那么两圆的连心线经过切点；（2）两圆相交，连心线垂直平分相交圆的公共弦。

直线与圆的位置关系切线长定理在几何学中，直线与圆的位置关系一直是一个重要的研究课题。

其中，切线长定理是直线与圆的位置关系中的一个重要定理，它在解决直线与圆的位置关系问题时起着至关重要的作用。

本文将介绍切线长定理的定义、推导过程及其应用。

一、切线长定理的定义切线长定理是指直线与圆的位置关系中，一条直线与圆相切时，切线与切点之间的长度关系。

具体来说，切线长定理可以表述为：一条直线与圆相切时，切线与切点之间的长度平方等于切点到圆心的距离的平方减去圆的半径的平方。

切线长定理可以用公式表示为：PT^2 = PC^2 - r^2其中，PT表示切线与切点之间的长度，PC表示切点到圆心的距离，r表示圆的半径。

二、切线长定理的推导切线长定理的推导可以通过几何方法和代数方法来进行。

这里我们将介绍一种代数方法的推导过程。

假设圆的方程为(x-a)^2 + (y-b)^2 = r^2，其中(a, b)为圆心坐标，r为圆的半径。

直线的方程为y = kx + c，其中k为直线的斜率，c为直线的截距。

首先，我们要找到直线与圆相切的条件。

直线与圆相切的条件是直线与圆的切点只有一个，也就是直线与圆的方程组有且只有一个解。

将直线方程代入圆的方程中，得到一个关于x的二次方程：(x-a)^2 + (kx+c-b)^2 = r^2解这个方程，得到直线与圆相切的条件：Δ = (k^2+1)(c-b)^2 - (1+k^2)(a^2+b^2-r^2) = 0其中，Δ为方程的判别式。

当Δ=0时，直线与圆相切。

接下来，我们要求出切线与切点之间的长度。

设直线与圆的切点为P(x0, y0)，则切点到圆心的距离为：PC^2 = (x0-a)^2 + (y0-b)^2切线与切点之间的长度为：PT^2 = (x-x0)^2 + (y-y0)^2将直线方程代入PT^2的表达式中，得到：PT^2 = (x-x0)^2 + (kx+c-y0)^2将PT^2和PC^2代入切线长定理的公式中，得到：(x-x0)^2 + (kx+c-y0)^2 = (x0-a)^2 + (y0-b)^2 - r^2 化简上式，得到切线长定理的公式：PT^2 = PC^2 - r^2三、切线长定理的应用切线长定理在解决直线与圆的位置关系问题时起着重要作用。

直线与圆的切线与切点知识点总结在平面几何中，直线与圆的位置关系是一个重要的知识点，其中切线与切点的相关内容更是具有关键意义。

接下来，让我们详细地探讨一下这部分知识。

一、直线与圆的位置关系在开始深入研究切线与切点之前，我们先来了解一下直线与圆的基本位置关系，主要有以下三种：1、相离：直线与圆没有公共点。

此时圆心到直线的距离大于圆的半径。

2、相切：直线与圆有且仅有一个公共点，这个公共点就是切点。

圆心到直线的距离等于圆的半径。

3、相交：直线与圆有两个公共点。

圆心到直线的距离小于圆的半径。

通过判断圆心到直线的距离与圆半径的大小关系，我们可以确定直线与圆的位置关系。

二、圆的切线1、切线的定义当一条直线与圆只有一个公共点时，称这条直线为圆的切线，这个公共点称为切点。

2、切线的性质（1）切线与圆只有一个公共点。

（2）圆心到切线的距离等于圆的半径。

（3）切线垂直于经过切点的半径。

3、切线的判定（1）定义法：如果直线与圆只有一个公共点，那么这条直线是圆的切线。

（2）距离法：如果圆心到直线的距离等于圆的半径，那么这条直线是圆的切线。

（3）定理法：经过半径的外端并且垂直于这条半径的直线是圆的切线。

三、切点切点是直线与圆相切时的公共点，具有一些特殊的性质。

1、切点在圆上，满足圆的方程。

2、过切点的半径与切线垂直。

四、切线长从圆外一点引圆的两条切线，这一点到两切点的线段长度相等，这个长度称为切线长。

切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

五、切线方程如果圆的方程为$（x a)＾2 ＋（y b)＾2 ＝ r^2$，点$P(x_0, y_0)＄在圆上，则切线方程为：＄（x_0 a)（x a) ＋（y_0 b)（y b) ＝ r^2$如果点$P(x_0, y_0)＄在圆外，设切线方程为$y y_0 ＝k(x x_0)＄，然后将其代入圆的方程，得到一个关于$x$的一元二次方程，令判别式等于 0，即可求出切线的斜率$k$，从而得到切线方程。