当前位置：文档之家 › 3空间一般力系

3空间一般力系

  • 格式：doc
  • 大小：1.74 MB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

空间一般力系

空间一般力系

Fy = −Fxy cos β = −F cosα cos β n
机械设计基础
§5-2 力对轴的矩
y
平面里的力对点之矩，实际是空间里力对轴之矩。 平面里的力对点之矩，实际是空间里力对轴之矩。
z
r r Mz (F) = Mo (Fxy ) =±Fxy ⋅ h
x
空间的力对轴之矩： 空间的力对轴之矩：
（a）力与轴平行，力对轴的力矩等于零； ）力与轴平行，力对轴的力矩等于零； ）、（c） （b）、（ ）力与轴相交，力对轴的力矩等于零； ）、（ 力与轴相交，力对轴的力矩等于零；
X Y Z 方向： 方向： cosα = , cos β = , cosγ = F F F
机械设计基础
⒍ 注意 力在坐标轴上的投影是代数量； 力在坐标轴上的投影是代数量；而力沿直角坐标轴的分量及 力在坐标平面上的投影是矢量。 力在坐标平面上的投影是矢量。 二、空间汇交力系的合成 ⒈ 几何法 与平面汇交力系的合成方法相同，也可用力多边形方法求 与平面汇交力系的合成方法相同， 合力。 合力。
⒊ 二次投影法（间接投影法） 二次投影法（间接投影法） 当力与各轴正向间夹角不易 确定时， 面上， 确定时，可先将 F 投影到xy 面上，然后再投影到x、y 轴 上。 X =F⋅sinγ ⋅cosϕ=F ⋅cosϕ=F⋅cosθ⋅cosϕ 即：
Y =F⋅sinγ ⋅sinϕ=Fxy ⋅sinϕ=F⋅cosθ⋅sinϕ Z = F ⋅ cosγ = F ⋅ sinθ
Fxy
作用点： 作用点： 物体和力矢的起点或终点 的接触之点。 的接触之点。
机械设计基础
一次投影法（直接投影法） ⒉ 一次投影法（直接投影法） 由图可知： 由图可知： X =F⋅cosα,

第三章空间力系习题解答

第三章空间力系习题解答
图3-34
3-10如图3-35所示的空间支架。已知：∠CBA=∠BCA=60°，∠EAD=30°，物体的重量为W=3kN，平面ABC是水平的，A、B、C各点均为铰接，杆件自重不计。试求撑杆AB和AC所受的压力FAB和FAC及绳子AD的拉力FT。
图3-35
3-11空间构架由三根直杆铰接而成，如图3-36所示。已知D端所挂重物的重量W=10kN，各杆自重不计。试求杆AD、BD、CD所受的力。
图3-41
3-17曲轴如图3-42所示，在曲柄E处作用一力F=30kN，在曲轴B端作用一力偶M而平衡。力F在垂直于AB轴线的平面内且与铅垂线成夹角a=10°。已知：CDGH平面与水平面间的夹角f=60°，AC=CH=HB=400mm，CD=200mm，DE=EG。不计曲轴自重，试求平衡时力偶矩M之值和轴承的约束反力。
习 题
3-1在边长为a的正六面体上作用有三个力，如图3-26所示，已知：F1=6kN，F2=2kN，F3=4kN。试求各力在三个坐标轴上的投影。
图3-26
3-2如图3-27所示，已知六面体尺寸为400 mm×300 mm×300mm，正面有力F1=100N，中间有力F2=200N，顶面有力偶M=20N·m作用。试求各力及力偶对z轴之矩的和。
图3-36
3-12空间桁架如图3-37所示。力F作用在ABDC平面内，且与铅垂线成45°角，ΔEAK≌ΔFBM，等腰三角形ΔEAK、ΔFBM和ΔNDB在顶点A、B和D处均为直角，又EC=CK=FD=DM。若F=10kN，试求各杆的受力。
图3-37
结点A
结点B
3-13三轮车连同上面的货物共重W=3kN，重力作用点通过C点，尺寸如图3-38所示。试求车子静止时各轮对水平地面的压力。
图3-42

力学第三章空间力系

力学第三章空间力系

第三章空间力系二、基本内容1. 基本概念1) 力在空间直角坐标轴的投影(a) 直接投影法：巳知力F 和直角坐标轴夹角a 、丫,则力F 在三个轴上的投 影分别为X = F cos aZ = Feos/(b) 间接投影法(即二次投影法)：巳知力F 和夹角八°,则力F 在三个轴上的 投影分别为X = F sin/cos^9Y = F sin/sin 。

Z = F cos/2) 力矩的计算(a) 力对点之矩—、目的和要求能熟练地计算力在空间直角坐标轴上的投影。

熟练掌握力对点之矩与力对轴之矩的计算。

对空间力偶的性质及其作用效应有清晰的理解。

了解空间力系向一点简化的方法，明确空间力系合成的四种结果。

能正确地画出各种常见空间的约束反力。

会应用各种形式的空间力系平衡方程求解简单空间平衡问题。

对平行力系中心和重心应有清晰的概念，能熟练地应用坐标公式求物体 的重心。

1、2、3、4、5、6^ 7、在空间情况下力对点之矩为一个定位矢量，其定义为i j kM0(F) = rx F = x y z = (yZ - zY)i + (zX - xZ)j + (xY - yX)kX Y Zr = xi + yj + zk F = Xi+ Yj + Zk其中尸为力尸作用点的位置矢径(b)力对轴之矩在空间情况下力对轴之矩为一代数量，其大小等于此力在垂直于该轴的平面上的投影对该轴与此平面的交点之矩，其正负号按右手螺旋法则来确定，即M Z(F) = ±F u,h = +2AOAB在直角坐标条下有Mx (乃=yZ-zY M y (F)=zX-xZ M z (F) =xY-yX(c)力矩关系定理力对己知点之矩在通过该点的任意轴上的投影等于同一力对该轴之矩。

在直角坐标系下有Mo(F)^M x(F)i+My(F)j+M2(F)k(d)合力矩定理空间力系的合力对任一点之矩等于力系中各力对同一点之矩的矢量和，即Mo g)二 W, (F)空间力系的合力对任一轴(例如z轴)之矩等于力系中各力对同一轴之矩的代数和，即M z(F R)=ZM z(F)=Z(xY-yX)3)空间力偶及其等效条件(a)力偶矩矢空间力偶对刚体的作用效果决定于三个要素(力偶矩大小、力偶作用面方位及力偶的转向)，它可用力偶矩矢肱表示。

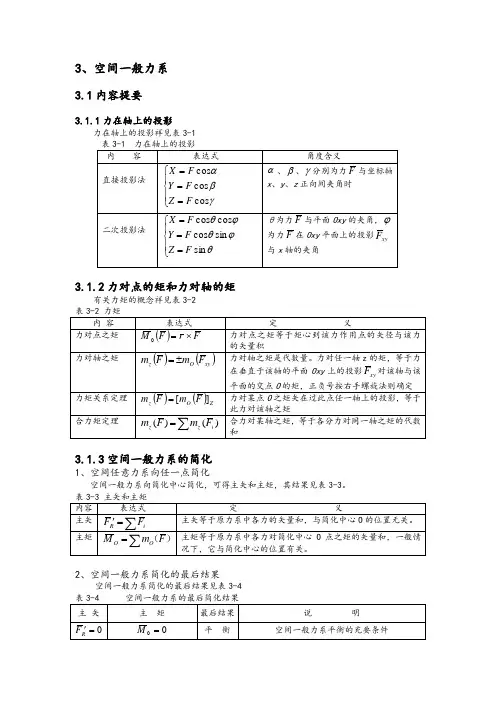
空间一般力系

空间一般力系

3、空间一般力系3.1内容提要3.1.1力在轴上的投影力在轴上的投影祥见表3-13.1.2力对点的矩和力对轴的矩有关力矩的概念祥见表3-23.1.3空间一般力系的简化1、空间任意力系向任一点简化空间一般力系向简化中心简化，可得主矢和主矩，其结果见表3-3。

2、空间一般力系简化的最后结果空间一般力系简化的最后结果见表3-43.1.4空间一般力系的平衡空间一般力系是力系的最一般形式，其平衡的充要条件是，力系的主矢和对任一点O 的主矩都等于零，即0='R F ，00=M空间力系的平衡方程见表3-5。

3.2解题要点1、 空间一般力系的题型可分为空间力系的简化问题和平衡问题两大类。

物体在空间力系作用下的平衡问题的解题方法和步骤与平面问题基本相同。

但求解空间问题时，要有清晰的空间概念，熟练掌握力在轴上的投影和力对轴之矩。

3、为了简化计算，在选取投影抽与力拒轴时，投影轴要与尽可能多的未知力或其所 在的平面相垂直，力矩轴应与尽可能多的未知力相交或平行．投影轴不一定要彼此垂直， 也不一定要与力矩轴相重合。

在列平衡方程时，可用适当的力矩方程取代投影方程，即 可采用四矩式、五矩式或六矩式的平衡方程，只要所建立的平衡方程是彼此独立的，就能 解出全部未知量。

4.解空间力系平衡问题时，有时采用将该力系向三个相互垂直的坐标平面投影的方 法，将空间力系化为三个平面力系分别求解。

采用此法时，必须注意各力在投影面上投 影的大小、方向及作用点的位置。

3.3范例分析例3-1 图3-1(a)为直角三棱柱。

其上作用力系：:F 1=200 N,22F F '==100N ，试求该力系在各轴上的投影及对轴之矩。

图3-1解解题思路： F 1在轴上的投影可按直接投影法计算，对轴之矩可用力对轴之矩的解析式计算；22F F '与组成一个空间力偶矩矢M 1=F 2×0.2=20N ·m ，如图（b ）所示，对轴之矩直接投影即可。

空间力系

空间力系

第三章 空间力系一、空间汇交力系（一）空间汇交力系的合成 1．空间力在坐标轴上的投影 （1）一次投影法如图3-1所示,若已知力F 与三个坐标轴x,y,z 间的夹角分别为θ、β和γ，则力F 在三个坐标轴上的投影分别为⎪⎭⎪⎬⎫===γβθcos cos cos z y x F F F （3.1）图3-1相应的，若已知力F 的三个投影，可以求出力F 的大小和方向，即大小为 222z y x F F F F ++=（3.2）方向 ⎪⎪⎪⎭⎪⎪⎪⎬⎫===F FF F F F z yx γβθcos cos cos（3.3）（2）二次投影法如图3-2所示,若已知力F 与坐标轴Oxy 的仰角γ以及力F 在Oxy 平面上的投影xy F 与x 轴间的夹角ϕ，则力F 在三个坐标轴上的投影分别为γϕλϕγsin sin in cos in F F Fs F Fs F z y x ===，，图3-22．合力投影定理 合力在某轴上的投影，等于各分力在同一坐标轴上投影的代数和。

即∑=+++=xixn x x Rx FF F F F 21 同理 ∑∑==ziRz yi RyF F F F ，3．空间共点力系的合成空间共点力系可以合成为一个合力，该合力的作用线通过力系的公共作用点，合力的大小和方向为()()()222∑∑∑++=zyxR F F F F （3.4）()()()⎪⎪⎪⎭⎪⎪⎪⎬⎫===∑∑∑R z R R yRR xRF F F F F F k F j F i F ,cos ,cos ,cos（3.5）（二）空间汇交力系的平衡 1．空间汇交力系的平衡条件空间汇交力系平衡的充要条件是合力等于零，即()()()0222=++=∑∑∑zyxR F F F F2．空间汇交力系的平衡方程根据平衡条件，得到空间汇交力系的平衡方程为⎪⎪⎭⎪⎪⎬⎫===∑∑∑000y x zFFF（3.6）利用上述三个方程，可以求解3个未知量。

02第二讲：刚体的平衡方程

02第二讲：刚体的平衡方程
i=1 i=1 i=1 n i=1 n
n
n
FR = ( ∑ Fx ) 2 + ( ∑ Fy ) 2 + ( ∑ Fz ) 2
M O = (∑ M Ox )2 +(∑ M Oy )2 +(∑ M Oz )2
空间任意力系平衡的充分必要条件： 空间任意力系平衡的充分必要条件：
∑ MOx (F ) = 0 ∑ M x (F ) = 0 ∑ Fx = 0 FR = 0 ⇔ ∑ Fy = 0 MO = 0 ⇔ ∑ MOy (F ) = 0 = ∑ M y (F ) = 0, MOz (F ) = 0 ∑ M z (F ) = 0 ∑ ∑ Fz = 0 10
平面任意力系平衡的充分必要条件： 平面任意力系平衡的充分必要条件：
y
一矩式
O
x
∑F = 0 x ∑MA(F) = 0 ∑MB(F) = 0
∑ Fx = 0 ∑ Fy = 0 ∑ M O ( F ) = 0
二矩式
三矩式
∑MA(F) = 0 ∑MB(F) = 0 ∑MC (F) = 0
– 力系中各力的大小、方向、作用点、力系的简化点A。 力系中各力的大小、方向、作用点、力系的简化点 。
• 输出结果
– 力系的主矢（大小和方向或用分量表示） 力系的主矢（大小和方向或用分量表示） – 力系对 点的主矩（大小和方向或用分量表示） 力系对A点的主矩（大小和方向或用分量表示） 点的主矩 – 力系简化的最简结果
FAy F A x
A
B
W
F B
∑ Fx = 0 C ∑ Fy = 0 W ∑ M O ( F ) = 0
讨论： 讨论： 二矩式和三 矩式的应用

第3章-平面与空间一般力系

第3章-平面与空间一般力系
【解】 土压力 FR 可使挡土墙绕A点倾覆，
故求土压力 FR使墙倾覆的力矩，就是求 FR
对A点的力矩。由已知尺寸求力臂d不方便，但如果将
FR分解为两分力 F1 和 F2
M A (FR ) M A (F1) M A (F2 )
F1h / 3 F2b
，
＝FR cos 30
＝150kN 3
1h3.5m -F1R50siknN301h1.5m
注意：主矢与简化中心位置无关，主矩则有关。因此说
到力系的主矩时，必须指出是力系对于哪一点的主矩。
主矢的解析表达法
R RX 2 RY 2
RX X1 X 2 X n X1 X 2 X n X
同理： RY Y
R X 2 Y 2
Tan RY Y RX X
M0=∑M0=M0(F1)+M0(F2)+…M0(Fn)=∑M0(F)
又B处的支座反力垂直于支持面，要形成与已知力偶M反向的 力偶，B处的支座反力 FB 方向只能斜向上，A处的支座反力
FA 的方向斜向下，作用线与 FB 平行，且有 FA FB
n
由平衡条件 Mi 0 ，得： i 1
FB d M 0
30°
FB (4m sin 30 ) 20MkN m 0
n
Mi 0
i 1
【例题3-3】 如图3-10(a)所示的简支梁AB，受一力偶的作用。
已知力偶 M 20kN m ，梁长l 4m ，梁的自重不计。 求梁A、B支座处的反力。
30°
M
A B
4m
60°
d
M
A FA
B FB 4m
【解】 取梁AB为研究对象，梁AB上作用一集中力偶M且保持 平衡，由于力偶只能用力偶来平衡，则A、B处的支座反力必形 成一对与已知力偶M反向的力偶

空间力系的平衡方程式及其应用

空间力系的平衡方程式及其应用

即与各坐标轴相交。因此各力对坐标轴的矩均为零，即式（3-17）中，
M x (F ) 0 ， M y (F ) 0， M z (F ) 0 。于是，空间汇交力系的平衡方程
只有三个，即
Fx 0
Fy
0
Fz
0
（3-18）
（2）空间平行力系
若取z轴平行于力系中各力的作用线，则 Oxy 坐标面与各力作用线
衡的必要与充分条件是：力系的主矢和力系对于任意点的主矩矢
都等于零。即
FR 0
MO 0
根据式（3-14）和式（3-16），上述条件可写成
空间任意力系平衡的必要与充分条 件是：力系中各力在任一直角坐标 系中每一轴上的投影的代数和等于 零，以及各力对每一轴的矩的代数 和也等于零。
Fx 0
Fy 0
式中，负号表明 FB ，FC 的实际方向与假设相反，即两杆均受压力。
例3-4
O1 和 O2 圆盘与水平轴 AB 固连，O1 盘垂直于z轴，O2 盘垂直于x轴，
力的矢量和。
即
FR F1 F2 Fn Fi （3-11）
图3-9
附加力偶系可合成为一个空间力偶，其力偶矩 MO，等于各附加力
偶矩的矢量和，亦即等于原力系中各力对于简化中心O的矩的矢量和。
MO MO (F1) MO (F2 ) MO (Fn ) MO (Fi )
F称R 为原力系的主矢，称为原力系对简化中心O的主矩矢 M。O
Fz 0
M
x
(F
)
0
M y (F ) 0
M
z
(F
)
0
（3-17）
空间任意力系是物体受力的最一般情况，其他类型的力系都可 以认为是空间任意力系的特殊情形，因而它们的平衡方程也可 由方程式（3-17）导出，具体如下。

工程力学教学课件模块3空间力系

工程力学教学课件模块3空间力系
转动的力矩为正，顺时针转动的力矩为负。力矩
的单位为N•m或kN•m。
由上述结论可知，力的作用线与轴相交或平
行时，力对轴之矩等于零。
提
示
3.2.2 合力矩定理
在平面力系中推导出来的合力矩定理对空间力系也同样适用，即空间力系中的合力对某轴之
矩等于力系中各分力对同一轴之矩的代数和，其表达式为
在计算力对轴之矩时，有时应用合力矩定理会使计算变得简单：先将力F沿空间直角坐标轴
Fz=Fsin 60°=600×0.866=520（N）
19
3.2.2 合力矩定理
20
3.2.2 合力矩定理
（2）计算力对轴之矩。先将力F在作用点处沿x、y、z方向分解，得到
三个分量Fx、Fy、Fz，它们的大小分别等于投影Fx、Fy、Fz的大小。
根据合力矩定理，可求得力F对指定的x、y、z轴之矩。
（b）所示。
先将力F向Axy平面和Az轴投影，得到Fxy和Fz；再将Fxy向x、y轴
投影，得到Fx和Fy。于是，有
Fx=Fxycos 45°=Fcos 60°cos 45°=600×0.5×0.707=212（N）
Fy=Fxysin 45°=Fcos 60°sin 45°=600×0.5×0.707=212（N）
力FNA、FNB、FNC的作用下保持平衡，各力的作
用线相互平行，构成空间平行力系。
3.3 空间力系的平衡方程
30
3.3 空间力系的平衡方程
（2）根据各力的作用线方向与几何位置，建立空间直角
坐标系Hxyz（点H为坐标原点）。
（3）列平衡方程并求解。
∑Fz=0，FNA+FNB+FNC-G=0
∑Mx（F）=0，FNC-G=0

理论力学3—空间力系解析

理论力学3—空间力系解析

以矩心O为原点建立坐标系，则
MO(F)
F
r xi y j zk F Fx i Fy j Fz k
kr Oj
ih x
A(x,y,z) y
3.2 力对点的矩和力对轴的矩
i jk MMOO(F))(r FF) = (xxi yjy zk )z(iFxi jFy j kFzk )
M O (FF)x rFy F F=z x y z MO(F()yFz(rzFF)y )i(xi(zFyxj xzkF)z)F(jxFxi(xFFyFyy jFyzFFzxk))k
3.2 力对点的矩和力对轴的矩
例3-4
已知： F,l, a,
求：M x F , M y F , M z F
解：把力 F 分解如图
M x F F l a cos M y F Fl cos
M z F F l a sin
3.2 力对点的矩和力对轴的矩
3 力对轴的矩的解析表达式
§3.3 空间力偶
1、力偶矩以矢量表示－－力偶矩矢
F1 F2 F1 F2
空间力偶的三要素 （1） 大小：力与力偶臂的乘积； （2） 方向：转动方向； （3） 作用面：力偶作用面。
§3.3 空间力偶 M rBA F
§3.3 空间力偶
2、力偶的性质 (1）力偶中两力在任意坐标轴上投影的代数和为零 . （2）力偶对任意点取矩都等于力偶矩，不因矩心的改
3.1 空间汇交力系
2 空间汇交力系的合成与平衡 （1）合成 将平面汇交力系合成结果推广得：
FR F1 F2 F n Fi 或 FR Fx i Fy j Fz k
合力的大小和方向为：
FR ( Fx )2 ( Fy )2 ( Fz )2
cos(FR

工程力学—空间力系力的投影

工程力学—空间力系力的投影
第三章 空间力系 空间一般力系：各力的作用线在空间任意分布的力系。
平面汇交力系、平面平行力系、平面一般力系都是它的特 殊情况。
设直角坐标系Oxyz如
图所示，已知力 与 F
x﹑y﹑z 轴间的夹角分别为
z
﹑ ﹑ 。 则力 在 F
x﹑y﹑z 轴上的投影Fx﹑ Fy﹑Fz 分别为：
Fx F cos
Fz F Fx o
y
Fy F cos
x
Fy
Fz F cos
注意
Fx﹑Fy﹑Fz为代数量。
二次投影法
z
Fx F sin cos Fy F sin sin Fz F
Fz F cos
力的正交分解
i、 j、k分别为x、y、z
Fx o
x
Fy
y
Fxy
方向的单位矢量，若以 ﹑F
x、y、z 的三个正交分量，则
合力的大小为
F Fx2 Fy2 Fz2 1643 N
合力与 x、y、z 轴的夹角分别为
arccosFx arccos 300 79o29
F
1643
arccosFy arccos 600 68o35
F
1643
arccosFFz arccos11654030
arccos(0.9130 ) 155 o55
F Fz
Fx Fy
x
﹑F
y分F别z表示
沿直F角坐标轴
F Fx Fy Fz Fxi Fy j Fzk
已知力的三个投影，求力的大小和方向的公式
F Fx2 Fy2 Fz2
arccosFxFΒιβλιοθήκη arccosFyF
注意
arccosFz
F
力的投影和分量的区别：

第三章 空间力系

第三章 空间力系

第三章 空间力系一、 判别题（正确和是用√，错误和否用×，填入括号内。

） 4-1 力对点之矩是定位矢量，力对轴之矩是代数量。

（ √ ）4-2 当力与轴共面时，力对该轴之矩等于零。

（ √ ）4-3 在空间问题中，力偶对刚体的作用完全由力偶矩矢决定。

（ √ ）4-4 将一空间力系向某点简化，若所得的主矢和主矩正交，则此力系简化的最后结果为 一合力。

（ √ ）4-5 某空间力系满足条件：ΣΣΣΣy x y F 0,Z 0,M (F )0,M (F )0====，该力系简化的最后结果可能是力、力偶或平衡。

（ √ ）4-6 空间力对点之矩矢量在任意轴上的投影，等于该力对该轴之矩。

（ × ） 4-7 空间力对点之矩矢量在过该点的任意轴上的投影等于该力对该轴之矩。

（ √ ） 4-8 如果选取两个不同的坐标系来计算同一物体的重心位置，所得重心坐标相同。

（ × ）4-9 重心在物体内的位置与坐标系的选取无关。

（ √ ）4-10 如题图4-10所示，若力F 沿x 、y 、z 轴的分力为F x 、F y 和F z ，则力F 在x 1轴上的投影等于F x 和F z 在x 1轴上的投影的代数和。

（ √ ）4-11 在题图4-10中，当x 1轴与z 轴间的夹角⎪⎭⎫ ⎝⎛=c b arctg ϕ时，力F 才能沿x 1轴和y 轴分解成两个分量。

（ √ ） 4-12 由n 个力系组成的空间平衡力系，若其中（n -1）个力相交于A 点，则另一个力也一定通过A 点。

（ √ ）4-13 空间汇交力系在任选的三个投影轴上的投影的代数和分别为零，则汇交力系一定平衡。

（ × ）4-14 某空间力系由两个力组成，此二力既不平行，又不相交，则该力系简化的最终结果为力螺旋。

（ √ ）4-15 空间任意力系的合力（如果存在合力）的大小一定等于该力系向任一点简化的主矢大小。

（ √ ）题4-10图4-16 任一平衡的空间汇交力系，只要A 、B 、C 三点不共线，则∑M A （F ） = 0，∑M B （F ） = 0和∑M C （F ） = 0是一组独立的平衡方程。

工程力学第3章空间力系的平衡

工程力学第3章空间力系的平衡
缺点
计算量大，需要较高的数学水平。
几何法求解空间力系平衡问题
几何法
通过几何图形来描述物体的运动状态和受力 情况，通过观察和计算几何关系得到物体的 运动轨迹和受力情况。
优点
直观易懂，适用于简单运动和受力情况。
缺点
精度低，容易受到主观因素的影响。
代数法求解空间力系平衡问题
1 2
代数法
通过代数方程来描述物体的运动状态和受力情况， 通过解代数方程得到物体的运动轨迹和受力情况。
平衡方程形式
空间力系的平衡方程为三个平衡方程，分别表示力在x、y、z轴上 的平衡。
空间力系的平衡方程应用
解决实际问题
利用空间力系的平衡方程，可以 解决实际工程中的受力分析问题， 如梁的受力分析、结构的稳定性 分析等。
简化问题
通过将复杂的问题简化为简单的 空间力系问题，可以更方便地求 解问题。
验证实验结果
优点
适用范围广，可以用于解决各种复杂问题。
3
缺点
计算量大，需要较高的数学水平。
04
空间力系平衡问题的实例分 析
平面力系的平衡问题实例分析
总结词
平面力系平衡问题实例分析主要涉及二维空间中的受力分析，通过力的合成与分解，确定物体在平面内的平衡状 态。
详细描述
在平面力系中，物体受到的力可以分解为水平和垂直方向的分力。通过分析这些分力的合成与平衡，可以确定物 体在平面内的稳定状态。例如，在桥梁设计中，需要分析桥墩受到的水平风力和垂直压力，以确保桥墩的稳定性。
平衡条件
物体在空间力系作用下，满足力矩平衡、力矢平衡和 力平衡三个条件。
空间力系的简化
01
02
03
力矩
描述力对物体转动效应的 量，由力的大小、与力臂 的乘积决定。

力学第四章空间力系

力学第四章空间力系
例4-3 如图所示的折杆，已知在其自由端A处受到 力F的作用。试求折杆固定端O的约束力。
§4－3 空间任意力系的平衡方程
解 取折杆为研究对象，画受力图如图所示,选直角坐 标系0xyz，列平衡方程
Fx = 0
FOx = 0
Fy = 0
FOy = 0
Fz = 0
FOz F = 0
Mx F = 0 MOx Fb = 0
§4－3 空间任意力系的平衡方程
平衡基本方程
空间任意力系平衡的充分必要条件：
各力在各坐标轴上的投影代数和分别等于零； 各力对各坐标轴的矩的代数和分别等于零
即：
Fx = 0
Fy = 0
Fz = 0
MxF = 0 M y F = 0 Mz F = 0
§4－3 空间任意力系的平衡方程
§4－3 空间任意力系的平衡方程
例4-5 用空间平衡力系的平面解法重解例4-4 解 重物匀速上升,鼓轮作匀速转动,即处于平衡姿态。取鼓轮为研究 对象。将力G和Q平移到轴线上，分别作垂直平面、水平平面和侧垂直
平面(图a、b、c)的受力图。
a)
c) b)
§4－3 空间任意力系的平衡方程
由(图a、b、 c)，列平衡方程。
§4－2 力对轴之矩
力对轴之矩（N·m）：度量力使物体绕轴的转动效应
M z (F ) = M O (Fxy ) = Fxyd
结论：力对某轴之矩是力使物体绕该轴 转动效应的度量，其大小等于力对垂直 于某轴平面内力对O点（即某轴在该面 的投影点）之矩。
力对轴之矩的符规定：
§4－2 力对轴之矩
例4-1 图示力F作用在圆轮的平面内,设力F作用线距z轴 距离为d。试计算力F对z轴之矩。
符号规定：从投影的起点到终点的方向与相应坐标轴 正向一致的就取正号；反之，就取负号。

第四章4-1,2,3

第四章4-1,2,3
FAx 0 A
y x C
θ
P B
l /2 RB
m d
l /2
FAy
∑ Fx = 0 ∑ Fy= 0
FAx - P cosθ = 0 FAy - P sinθ + RA = 0
FAx = P cosθ θ
m 1 FAy = + Psin θ l 2
例4-4:塔式起重机如图所示.设机身的重力为G1,载重的 重力为G2 ,距离右轨的最大距离为L,平衡重物的 重量为G3 ,求起重机满载和空载均不致翻倒时, 平衡重物的重量G3所满足的条件.
G1 F q2 Fq1 q
L G2
d1 B qm d2
mA A FAx FAy
L
G2
列平衡方程求解: 列平衡方程求解 ∑Fx = 0 FAx -Fq1 = 0
y C G1 H h d1 B d2 Fq1
1 h 3
Fq2
0
1 l 2
x
1 1 FAx = Fq1 = q m h = γ 1 h 2 2 2
a G3 e
C G1 L A b B
G2
解:取起重机为研究对象,画出受力图 取起重机为研究对象, 1,满载时,当重物距离右轨最远时,当起重机平衡时: ,满载时,当重物距离右轨最远时,当起重机平衡时: ∑ mB(F) = 0 - G1 e- G2 L- NA b+ G3 (a+ b) = 0 ) NA =[ -G1 e- G2 L+ G3 ( a+ b)]/b ) 起重机不翻倒的条件为: 起重机不翻倒的条件为: NA ≥0 G3 ≥( G1 × e+ G2 × L)/( a+ b) ( ) G3 a C e G 1 L B b NB

空间一般力系

空间一般力系
3
§4–1 空间一般力系的简化
设空间一般力系（F1，F2，……，Fn）中各力作用于刚体 上P1，P2，……，Pn各点。
在刚体上任选一点O作为简化中心。
FR Fi
F1 P1
F2 P2
力系等效定理
MO M Oi FR
O
Pn
O
MO
Fn
4
FR Fi MO M Oi
➢ 空间一般力系向任一点简化可得到一个力和一个力偶。 ➢ 这个力通过简化中心，称为力系的主矢，它等于各 个力的矢量和，并与简化中心的选择无关。 ➢ 这个力偶的力偶矩矢称为力系对简化中心的主矩， 并等于力系中各力对简化中心之矩矢的矢量和，并 与简化中心的选择有关。
主视图：yz平面
z
50
200
FAz A FAy C FAx
x 20o Q
FBz B
FBx
100
D Py y
Px Pz
Fy 0
FAy Py 0 FAy Py 352(N)
MA 0
200FBz 300Pz 50Q sin200 0
z
FBz 2040(N)
Qz
FAz
FAy CA
FBz
Pz
FR
d O' O
MO //
力螺旋
d MO FR
9
§4–2 空间一般力系的平衡
一、空间一般力系的平衡条件
FR
0
MO 0
空间一般力系平衡的充分与必要条件 是主矢量和对任一点的主矩都等于零。
二、空间一般力系的平衡方程
FR
Fxi 2
Fyi 2
Fzi 2
MO
空间一般力系平衡的充要条件是：
各力在三个坐标轴上的投影的代数和及各力对三个轴 力矩的代数和都必须分别等于零。 共六个独立方程，只能求解独立的六个未知数。 投影轴和取矩轴可以任意选择，但六个方程必须线性无关。 空间一般力系的平衡方程的其它形式：四矩式，五矩式，六

理论力学 第3章

理论力学 第3章

• 作业： • 习题 3-6，3-12
§ 3-5 空间任意力系的平衡方程
1. 空间任意力系的平衡方程 空间任意力系平衡的必要和充分条件：
该力系的主矢r 和对于r 任一点的主矩都为零 FR 0, MO 0
Fx 0 Fy 0 Fz 0
Mx 0 My 0 Mz 0
所有各力在三个坐标轴中每一个轴上的投影的 代数和等于零，以及这些力对于每一个坐标轴的 矩的代数和也等于零。
解析法表示:
M M xi M y j M zk
Mx 0 My 0 Mz 0
——空间力偶系的平衡方程
例3-5 已知：在工件四个面上同时钻5个孔，每个 孔所受切削力偶矩均为80N·m.
求：工件所受合力偶矩在 x, y轴, z上的投影.
解：
把力偶用力偶矩 矢表示，平行移到 点A .
Mx Mix M3 M4 cos45 M5 cos45 193.1N m
力螺旋 由一力和一力偶组成的力系，其中
的力垂直于力偶的作用面
（1）FR 0, M O 0, FR // M O
中心轴过简化中心的力螺旋
钻头钻孔时施加的力螺旋
r r rr （2）FR 0, MO 0,既FR不, M平O行也不垂直，成任意夹
角
力螺旋中心轴距简化中心为 d M O sin
FR
F1 F2 3.54kN FA 8.66kN
§ 3-2 力对点的矩和力对轴的矩
1. 力对点的矩以矢量表示——力矩矢
力对点之矩 在平面力系中——代数量 在空间力系中——矢量
MO (F) Fh 2ΔOAB
r MO
r (F
)
rr
r F
三要素：
（1）大小:力 F与力臂的乘积

03-理论力学-第一部分静力学第三章空间力系

03-理论力学-第一部分静力学第三章空间力系
F X i Y j Z k , r xi y j zk i jk MO(F) r F x y z
X
Y
Z
( yZ zY )i (zX xZ) j (xY yX )k
2 力对轴的矩
力使物体绕某一轴转动效应的度 量，称为力对该轴的矩。
16
力对轴的矩的定 义 M z (F ) MO (Fxy )
力系简化的计算 计算主矢的大小和方向
FRx X , FRy Y , FRz Z
FR FRx2 FRy2 FRz2
cos FRx ,
FR
cos FRy ,
FR
cos FRz
FR
计算主矩的大小和方向
MOx M x (F ) , MOy M y (F ) ,
MOz M z (F )
与 z 轴共面
18
力对轴的矩的解析式
先看对z轴的矩:
M z (F ) MO (Fxy )
M O (Fy ) MO (Fx )
Fy x y Fx
xY yX
类似地，有：
M x (F) yZ zY M y (F ) zX xZ M z (F ) xY yX
Fy
Fx
Fxy
力对轴的矩的 解析表达式
3
§3 - 1 空间汇交力系 本节的主要内容有：
★ 空间力的投影；
★空间汇交力系的合成与平衡。
1 力在直角坐标轴上的投影和力沿直角坐标轴的
分解
(1) ■直接投影法
X F cos
Y F cos
Z F cos
也称为一次投影法
4
■间接投影法
Fx y F sin X Fxy cos F sin cos Y Fxy sin F sin sin

理论力学第三章 空间力系汇总

理论力学第三章 空间力系汇总

Pxy Pcos45
Px Pcos45sin60 Py Pcos45cos60
P 6 Pi 2 P j 2 Pk
4
4
2
r 0.05 i 0.06 j 0 k
MO(F) r F
i
j
k
0.05 0.06 0
6P 2P 2P
4
4
2
84.8 i 70.7 j 38.2 k
称为空间汇交力系的平衡方程. 空间汇交力系平衡的充要条件：该力系中所有各力在三个坐 标轴上的投影的代数和分别为零.
[例]三角支架由三杆AB、AC、AD用球铰A连接而成，并用球铰支座B、C、
D固定在地面上，如图所示。设A铰上悬挂一重物，已知其重量W=500N。
结构尺寸为a=2m，b=3m，c=1.5m，h=2.5m。若杆的自重均忽略不计，求
（2）何时MZ (F) 0
Mz (F) Mo(Fxy ) Fxy h
z
F
Fz
Fxy o
h
P
力与轴相交或与轴平行（力与轴在同一平面内），力对该轴 的矩为零.
（3) 解析表达式
M Z (F) MO (F xy ) MO (F x ) MO (F y )
xFy yFx
M x (F) yFz zFy
空间力偶的三要素
（1） 力偶矩大小：力与力偶臂的乘积； （2） 力偶矩方向：右手螺旋； （3） 作用面：力偶作用面。
转向：右手螺旋；
2、力偶的性质
(1）力偶中两力在任意坐标轴上投影的代数和为零 . （2）力偶对任意点的矩都等于力偶矩矢，不因矩心的改变而 改变。
M x (P) 84.8(N.m) M y (P) 70.7(N.m) M x (P) 38.2(N.m)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

3、空间一般力系内容提要力在轴上的投影力在轴上的投影祥见表3-1表3-1 力在轴上的投影力对点的矩和力对轴的矩有关力矩的概念祥见表3-2空间一般力系的简化1、空间任意力系向任一点简化空间一般力系向简化中心简化，可得主矢和主矩，其结果见表3-3。

2、空间一般力系简化的最后结果空间一般力系简化的最后结果见表3-4空间一般力系的平衡空间一般力系是力系的最一般形式，其平衡的充要条件是，力系的主矢和对任一点O 的主矩都等于零，即0='R F ，00=M空间力系的平衡方程见表3-5。

解题要点1、 空间一般力系的题型可分为空间力系的简化问题和平衡问题两大类。

物体在空间力系作用下的平衡问题的解题方法和步骤与平面问题基本相同。

但求解空间问题时，要有清晰的空间概念，熟练掌握力在轴上的投影和力对轴之矩。

3、为了简化计算，在选取投影抽与力拒轴时，投影轴要与尽可能多的未知力或其所 在的平面相垂直，力矩轴应与尽可能多的未知力相交或平行．投影轴不一定要彼此垂直， 也不一定要与力矩轴相重合。

在列平衡方程时，可用适当的力矩方程取代投影方程，即 可采用四矩式、五矩式或六矩式的平衡方程，只要所建立的平衡方程是彼此独立的，就能 解出全部未知量。

4.解空间力系平衡问题时，有时采用将该力系向三个相互垂直的坐标平面投影的方 法，将空间力系化为三个平面力系分别求解。

采用此法时，必须注意各力在投影面上投 影的大小、方向及作用点的位置。

范例分析例3-1 图3-1(a)为直角三棱柱。

其上作用力系：:F 1=200 N,22F F '==100N ，试求该力系在各轴上的投影及对轴之矩。

图3-1解解题思路： F 1在轴上的投影可按直接投影法计算，对轴之矩可用力对轴之矩的解析式计算；22F F '与组成一个空间力偶矩矢M 1=F 2×=20N ·m ，如图（b ）所示，对轴之矩直接投影即可。

)N ( 28.742922004.03.02.02.02221=⨯=++=F F x)N ( 56.1482942002941=⨯==F F y)N ( 41.1112932002931-=⨯-=-=F F z)m N ( 56.44041.1114.0)(⋅-=-⨯-=-=y z x zF yF M)m N ( 28.341241.1112.053)(1⋅=+⨯=+-=M xF zF M z x y 154)(M yF xF M x y z +-=)m N ( 161628.44.056.1482.0⋅=+⨯-⨯=7例3-2均质矩形板ABCD 重P=200 N ，作用在其对角线交点上，矩形板用球形铰链A 和蝶形铰链B 固定在墙上，并用绳子CE 维持在水平位置如图3-2（a ）所示，若α=30°，试求绳子的拉力以及铰链A,B 的反力。

图3-2解解题思路：取矩形板为研究对象，空间球形铰链A 的约束反力可用三个互相垂直的分力来表示。

而蝶形铰链轴向的约束反力和垂直于轴向的约束力偶可以忽略，故约束反力的作用线在垂直于铰链轴的平面内。

作用在板上的力组成一个空间任意力系，它有六个平衡方程，可求解六个未知力。

（1）取矩形板为研究对象，受力图如图（b ）所示。

为便于计算绳子拉力F 对x ，y 轴之矩，可将力F 分解成平行于z 轴的分力F z =F sin30°，与在板平面内的分力F xy =F cos30°。

（2）建立空间任意力系的平衡方程：0)(=∑F m z ， 0=Bx F （1） 0)(=∑F m y ，030sin 21=⋅︒-⨯BC F BC P （2） N F 200=0)(=∑F m x ，030sin 21=⋅︒+⨯-⋅CD F AB P AB F Bz （3）0=Bz F0=∑X ，060cos 30cos =︒⋅︒-+F F F Bx Ax （4）N 6.86=Ax F0=∑Y ， 030cos 30cos =︒⋅︒-F F Ay （5）N 150=Ay F0=∑Z ， 030sin =︒+-+F P F F Bz Az （6）N 100=Az F[讨论]空间力系的平衡方程建立次序可以随意，一般，首先建立的是不用解联立方程的力矩平衡方程。

应尽可能使一个方程包含一个未知量，使未知量从方程中直接解出。

最后还可以用非独立的平衡方程来校核所得约束力。

如对DB 线用0=∑DB M 平衡方程来校核力F ，F Az 的例3-3 图3-3（a ）所示电杆OD 高7m ，D 处受水平力F =10kN 作用。

O 处视为球铰支座，A 处以钢索AB 、AC 与地面相连，略去电杆自重。

试求钢索拉力及支座反力。

解：解题思路：电杆OD 受已知力F 、钢索的拉力F 1与F 2以及球铰支座O 处的反力F Ox 、F Oy 、F Oz 作用，计有5个未知量，可由空间一般力系平衡方程的基本形式求解。

OD 杆的受力如图（b ）所示。

对图示坐标系，列平衡方程图3-30=∑X ， 0sin 45cos sin 45cos 21=+︒-︒Ox F a F a F （1）0=∑Y ， 0cos 45cos cos 45cos 21=+︒+︒+-Oy F a F a F F （2）0=∑Z ， 045cos 45cos 21=︒-︒-F F F Oz （3） 0)(=∑F m x ， 0445sin 445sin 721=⋅︒-⋅︒-⋅F F F （4）0)(=∑F m y 0345sin 345sin 21=⋅︒-⋅︒F F （5）由图示几何关系知：53sin =a ，54cos =a 联立求解上述5个平衡方程，可得kN 37.1221==F F ，F Ox =0，F Oy =–4 kN ，F Oz = kN其中，负号表示约束反力的实际方向与假设的方向相反。

讨论 为了避免解联立方程组，如何合理选取力矩轴理论依据是当力与轴相交或平行时，力对该轴之矩等于零。

首先，欲使力矩平衡方程中不出现F 1及F 2 ，可过F 1、F 2交点A 作x '及y '轴（图b ），此时力F 、F Oy 、F Oz 与y '轴共面，则这些力对y '轴之矩为零。

故应以y '轴为矩轴。

0)(=∑'F m y ，05=⋅-Ox F得0=Ox F同理，应以x '轴为矩轴列为矩平衡方程。

由于已求出00=X ，在下面建立平衡方程时，可不再考虑。

由0)(=∑'F m x ，052=⋅-⋅Oy F F得kN 452-=-=F F Oy其次以F 1、F 2的交线BC 为矩轴，即0)(=∑F m BC ，047=⋅-⋅Oz F F得kN 5.1747==F F Oz 最后，求F 1及F 2 。

分别以OC 及OB 为力矩轴，列出力矩平衡方程0)(=∑F m OC ， 0)290cos(225sin 71=-︒⋅⋅+⋅-a F a F 0)(=∑F m OB ， 0)290cos(225sin 72=-︒⋅⋅-⋅a F a F 可解出αααcos 257)290cos(225sin 721F F F F ⋅=-==kN 37.12542570==应注意到，在上式的力矩计算中，应用了力矩关系定理。

例如，当求)(1F m OC 时，是将力1F 对O 点之矩先表示为矩矢)(10F m ，再投影到OC 轴上。

在本例中还可应用对CG 及BE 轴的力矩平衡方程，以求解F 1及F 2 。

综上述可知，由于合理地选取了力矩轴，并以力矩方程代替了投影方程，使得每个未知量都可由一个平衡方程单独解出来。

既避免了解联立方程组，又可避免由于数值计算而产生误差的传播。

例3-4 在铅垂轴AB 上有一个水平圆盘。

A 点为向心轴承，B 点为止推轴承。

盘上C 点有力F 作用，在转轴上绕有一软绳，绳的一端悬挂有重物P ，如图3-4（a ）所示。

已知：P=100KN ，r 1=,r 2=, a=1m ,α=30°,β=60°.试求平衡时力F 及轴承反力。

解解题思路：先对z 轴取矩，列平衡方程，求出力F ，然后再求出A 及B 处的反力。

图3-4(1)选取AB 物体为研究对象，A 点具有两个方向的轴向约束,B 点具有三个方 向的轴向约束，将传动轴上软绳分割。

显然，分割后绳子的拉力为P 值。

物体的受力图见图(b)，为方便地建立平衡方程，可将力F 分解成三个轴向的分力，按二次投影法，可得各分力大小为：F x =Fcos60°cos30°，F y =Fcos 260°，F y =Fsin60°。

在作力F 的二次投影时，可以作辅助图（c ）来表示。

(2)按尽可能避免求解联立方程的原则建立方程：∑=0)(F m z， 060cos 21=︒-⋅r F rP得 F=80kN∑=0)(F mX， 030cos 232=︒-++-z y Ay F r aF aP aF得 F A y =63﹒3kN∑=0)(F m Y ， 030sin 32=︒++z x Ax F r aF aF 得 F Ax =–17﹒3kN ∑=0X ， 0=++x Bx Ax F F F 得： F Bx =–17﹒3kN ∑=0Y ， 0=--+y By Ay F P F F 得 F By =56﹒7kN∑=0Z ， 0=-z Bz F F 得 F Bz =69﹒3kN讨论：对空间一般力系的平衡问题，可先将空间力沿三个坐标轴方向分解，然后再列平衡方程求解，较为方便。

例3-5边长为a 的等边三角形板ABC 用三根铅直杆1、2、3和三根与水平面各成30°角的斜杆4、5、6支撑在水平位置。

在板的平面内作用有力偶M ，如图3-5(a)所示。

板和各杆的自重不计，求各杆的内力。

图3-5解：解题思路：因支撑三角板的杆都是二力杆，故用截面法将各杆截开，取三角板为研究对象，受力如图（b ）所示。

它们构成空间一般力系，有六个未知量，可用空间一般力系平衡方程式求解。

下面分别用三种方法求解。

[方法一]用空间力系一般形式的平衡方程式求解。

坐标系Dxyz 如图（b ）所示。

0)(=∑F M z ，030cos 30cos 5=+︒⋅︒M a F （1） 得 a Ma M F 3430cos 25-=︒-= 0=∑Y ，030cos 30cos 30cos 30cos 54=︒︒-︒︒F F （2） 得 aM F F 3454-== 0=∑X ，030sin 30cos 30sin 30cos 30cos 546=︒︒-︒︒-︒F F F （3）得 aMF F F 3430sin )(546-=︒+= 0)(=∑F M x ，030cos 30sin 30cos 42=︒⋅︒-︒-a F a F得 aMF F 3230sin 42=︒-= （4） 0)(=∑F M y ，030sin 30sin 30sin 30sin 5423=⋅︒-︒⋅︒-︒--a F a F a F a F （5） 得 aMF F F F 3230sin )30sin (5423=︒-︒--= 0=∑Z ，030sin 30sin 30sin 654321=︒-︒-︒----F F F F F F （6）得aMF F F F F F 3230sin )(654321=︒++---= 上述求得的结果为各杆内力的大小。