当前位置：文档之家 › 第三章 空间力系分解

第三章 空间力系分解

  • 格式：ppt
  • 大小：845.50 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

03第三章 空间力系

03第三章 空间力系

m (F) = m (F ) z O xy = m (F ) +m (F ) O x O y
即
m (F) = xY − yX z
同理可得其余两式，即有：
m (F) = yZ − zY x my (F) = zX − xZ m (F) = xY − yX z
力对轴的矩的解析式
三、力对点的矩与力对通过该点的轴之矩的关系 ⒈ 定理 力对点的矩矢在通过该点的 任意轴上的投影等于这力对于该 轴的矩。 轴的矩。这就是力对点之矩与对 通过该点轴之矩的关系。 通过该点轴之矩的关系。 ⒉ 证明
第3章 章 空 间 力 系
本章重点、 本章重点、难点
⒈重点
力在空间直角坐标轴上的投影和力对轴之矩。 力在空间直角坐标轴上的投影和力对轴之矩。 空间力系平衡方程的应用。 空间力系平衡方程的应用。 常见的空间约束及约束反力。 常见的空间约束及约束反力。
⒉难点
空间矢量的运算， 空间矢量的运算，空间结构的几何关系与立体 图。
四、空间力偶系的合成与平衡 ⒈ 合成 由于空间力偶系各力偶是自由矢量，只要不改变各分力偶 矩矢方向，将它们都滑移至某汇交点，它们的合成符合矢量合 成法则。 即：合力偶矩 = 分力偶矩的矢量和。
n i= 1
即： m = m +m +m +L m = ∑m + n 1 2 3 i
2 2 大小： m = mx ห้องสมุดไป่ตู้m2 +mz ; y
四、力对点的矩的解析求法 又由于
m (F) = r ×F O =[m (F)]xi +[m (F)]y j +[m (F)]z k O O O
=mx (F)i +my (F) j+mz (F)k

3空间力系正式解析

3空间力系正式解析
∑my(F)=0
上式表明空间平行力系平衡的必要和充分条件
图4.1
本章内容
4.1 力沿空间直角坐标轴的投影
4.2 力对轴之矩 4.3 空间力系的平衡方程 4.4 重心
4.1 力沿空间直角坐标轴的投影 4.1.1 一次投影法
设有一力F和空间直角坐标系Oxyz(图4.2)。
图4.2
如果力F与x、y、z轴所夹的锐角分别为α、β、γ，
则 Fx=±Fcosα Fy=±Fcosβ （4-1） Fz=±Fcosγ
Fy=±Fsinγsinφ
Fz=±Fcosγ
（4-2）
【例4.1】在一立方体上作用有三个力P1、P2、P3，如图 4.4所示。已知P1=2kN，P2=1kN,P3=5kN，试分别计算这 三个力在坐标轴x、y、z上的投影。 【解】力P1的作用线与轴x平行，与坐标面yOz垂直，与 轴y、z也垂直，根据力在轴上的投影的定义可得 P1x=-P1=-2kN P1y=0 P1z=0 力P2的作用线与坐标面yOz平行，与轴x垂直，先将 此力投影在x轴和yOz面上，在x轴上投影为零，在yOz面 上投影P2yz就等于此力本身；然后再将P2yz投影到y、z轴 上。
mz(F)=mO(F)=±Fd 在一般情况下，力F可能既不平行于z轴，又不 与z轴相交，也不在垂直于z轴的平面内，如图4.5(c) 所示。
力F使门绕z轴转动的效应完全由分力Fxy来确定。 分力Fxy使门转动的效应可用力Fxy对O点之矩来度量， 因此可得 mz(F)=mz(Fxy)=mO(Fxy)=±Fxyd （4-5）
4.1.2 二次投影法
如图4.3所示，如果已知力F与z轴的夹角γ及F和z 轴所形成的平面与x轴的夹角φ，为求出力F在三个坐 标轴上的投影，可先将力F投影到z轴及坐标平面xOy 上，在xOy平面上的投影为矢量Fxy，其大小为

第三章 第一节 空间力的分解与投影

第三章 第一节 空间力的分解与投影
3 cosa cos b cosg 3
O b
F
g a
y
3 Fx F cosa F 3 3 F y F cos b F 3 3 Fz F cosg F 3
x
方法二(二次投影法) z
sing cosg 2a 3a a 3a 2 3 3 3
F
O
b
Fx = Fcosa Fy = Fcosb Fz = Fcosg
Fy
x F = Fx + Fy + Fz
Fx =Fx i y Fy =Fy j iO j Fx Fz =Fz k x 力在轴上投影为代; Fz k
2.二次投影法 z Fz
g
Fz = Fcosg Fxy = Fsing 注意:力在平面上的投影Fxy为矢量 y Fx = Fxycosj = Fsing cosj Fy = Fxysinj = Fsing sinj
第三章 空间力系
空间力系：各力的作用线不在同一平面内的力系。 方法：采用力系向一点简化的方法进行研究。
本章我们将要学习的内容 空间力系的基本概念 空间力系的简化 空间力系平衡问题 重心
第一节 空间力的分解与投影
一、空间力的分解 z Fz O Fx F Fy y
a
二、空间力的投影 1. 直接投影法 z Fz k g F
F Fy Fxy
O
Fxj x
已知力在的投影，则可以确定该力的大小和方向。
F Fx2 F y2 Fz2 Fx cos a F cos b Fy F Fz cos g F
例(P71例3-1)在边长为a的正六面体的对角线上作用一力F。 试求该力分别在x、y、z轴上的投影。
z 解 方法一(直接投影法)

武汉理工大学理论力学课件 第三章 空间力系(第二版)资料

武汉理工大学理论力学课件 第三章 空间力系(第二版)资料

应该注意：力在轴上的投影是代数量， 而力在平面上的投影是矢量。
5
力沿直角坐标轴的分解
z
Fz F
F Fx Fy Fz Fx i Fy j Fz k
k
力F 在坐标轴上的投影和力F 沿坐
oj
标轴的正交分量间的关系为：
Fx i
Fy y
x
图4.3
Fx Fx i Fy Fy j Fz Fz k
cos(M,i)
M ix M
cos(M, j)
M iy M
cos(M,k)
M iz
M
25
空间力偶系的平衡条件 空间力偶系平衡的必要与充分条件是：合力偶
矩矢等于零，亦即所有力偶矩矢的矢量和等于零。
Mi 0
M ( Mix )2 ( Miy )2 ( Miz )2 0
欲使上式成立，必须同时满足：
一、力对点之矩以矢量表示－－力矩矢
三要素：
实例
(1) 大小:力F与力臂的乘积
F
(2) 方向:转动方向
(3) 作用面：力矩作用面。
9
力对点之矩的定义
MO(F) r F
力矩矢MO(F) 的 始端必须在矩心，
为定位矢量
MO F
大小： MO (F) r F F h 2AΔOAB
r
矩矢方向：按右手螺旋法则确定
Fy3 1500 cos sin 1073 N
Fz3 1500 sin 671N
7
例3.2 已知力沿直角坐标轴的解析式为F=3i+4j-5k(kN), 试求这个力的大小和方向。
解：Fx=3kN，Fy=4kN，Fz=-5kN
F ( Fx )2 ( Fy )2 ( Fz )2 5 2kN

第3章 空间力系

第3章 空间力系

４７第3章 空间力系本章要点● 理解力在空间直角坐标轴上的投影● 理解力对轴之矩● 掌握空间力系的平衡方程及其应用● 掌握重心及其计算前面我们讨论了平面力系，平面力系中各力的作用线分布在同一平面内，这是物体受力的特殊情况，现在将讨论物体受力的最一般的情况——空间力系。

当力系中各力的作用线不在同一平面，而呈空间分布时，称为空间力系。

本章主要介绍空间力系的简化与平衡问题。

在工程实际中，有许多问题都属于这种情况。

如图3-1所示车床主轴，受有切削力F x 、F y 、F z 和齿轮上的圆周力F t 、径向力F n 以及轴承A 、B 处的约束反力，这些力构成一组空间力系。

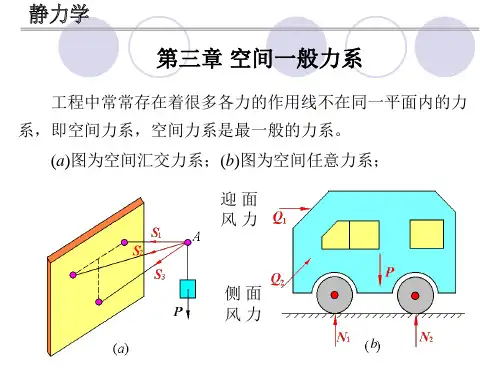
与平面力系一样，空间力系可分为空间汇交力系、空间平行力系及空间一般力系。

图3-1 车床主轴3.1 力在空间直角坐标轴上的投影在平面力系中，常将作用于物体上某点的力向坐标轴x 、y 上投影。

同理，在空间力系中，也可将作用于空间某一点的力向坐标轴x 、y 、z 上投影。

具体作法如下：1.直接投影法若一力F 的作用线与x 、y 、z 轴对应的夹角已经给定，如图3-2a 所示，则可直接将力F 向三个坐标轴投影，得⎪⎭⎪⎬⎫=== cos cos cos γβαF F F F F F z y x （3-1）４８其中，α、β、γ分别为力F 与x 、y 、z 三坐标轴间的夹角。

2.二次投影法当力F 与x 、y 坐标轴间的夹角不易确定时，可先将力F 投影到坐标平面xoy 上，得一力F xy ，进一步再将F xy 向x 、y 轴上投影。

如图3-2b 所示。

若γ为力F 与z 轴间的夹角，φ为F xy 与x 轴间的夹角，则力F 在三个坐标轴上的投影为⎪⎭⎪⎬⎫===== cos sin sin sin cos sin cos γϕγϕϕγϕF F F F F F F F z xy y xy x （3-2）图3-2 二次投影法具体计算时，可根据问题的实际情况选择一种适当的投影方法。

第三章 空间力系

第三章 空间力系

Ft tan Fa Ft tan Fr cos
第三章 空间力系
【课堂练习】图示力F作用在A点，此力在x轴、y轴、z轴 上的投影分别是多少？
第三章 空间力系
三、交于一点且互相垂直的三力的合成
力直角平行六面体法则
F＝
Fx2 Fy2 Fz2
Fx cosα＝ F
Fy cosβ＝ F
第三章 空间力系
（2）力F对各坐标轴之矩为： Mz(F )= Mz(Fx)+Mz(Fy)= -Fx· y+Fy· x= -10.98 N· m Mx(F )=Mx(Fy)+Mx(Fz)= -Fy· z-Fz· y= -105 N· m My(F)=My(Fx)+My(Fz)=Fx· z+Fz· x=53.3 N· m。
解：
（1）确定车刀刀尖为研究对象，以工件主轴为水平轴空间 直角坐标系。
第三章 空间力系
（ 2）刀尖受力分析
刀尖受到径向力Fx（沿x轴方向）、轴向力Fy（沿y轴方 向）、圆周力Fz（沿z轴方向）的作用。 （3）用力直角平行六面体法则求合力F 以三力Fx、Fy、Fz为棱边作一直角平行六面体，则此六面 体的对角线即为三力的合力F＝19.6 kN
第三章 空间力系 三、空间力系的平衡条件和平衡方程
力矢的主矢和力系对空间任意一点的主矩都等于零。
FR' 0
，
Mo 0
Fy =0 Fy=0 Fz=0 Fz =0 Mx(F )=0 Mz(F )=0
• 空间汇交力系力系 Fx =0 • 空间平行力系力系 Fy=0 • 空间任意力系力系 Fx=0 • 空间力偶系力系
第三章 空间力系 四、空间力系平衡的平面解法
1．确定研究对象，画出受力图。

第三章 空间力系


①力偶矩的大小= m 等于力偶的力与力偶臂的乘积。
②力偶矩的方位——垂直于力偶所在的平面
③指向——遵循右手螺旋规则。
空间力偶的等效定理 作用在同一刚体的两平行平面的两个力偶，若它们的转向相 同，力偶矩的大小相等，则两个力偶等效。 由此可见：空间力偶矩是自由矢量
21
例3-4 已知：在工件四个面上同时钻5个孔，每个孔所受切削 力偶矩均为80N· m. 求：工件所受合力偶矩在 x, y , z 轴上的投影
1、若FR' 0, MO , 0 则该力系平衡（后面专门讨论）。 2、若 FR' 0, MO 0 则力系可合成一个合力偶，其矩等于原
力系对于简化中心的主矩MO。此时主矩与简化中心的位置无 关。
3、若 FR' 0, MO 0 则力系可合成为一个合力，主矢 F ' R 等于原力系合力矢 FR ，合力 FR 通过简化中心O点。
My

F Fl cos
M z F F l a sin
18
19
五、空间力偶矩用矢量表示：
由于空间力偶除大小、转向外，还必须确定力偶的作用面， 所以空间力偶矩必须用矢量表示。 力偶的转向为右手螺旋定则。
从力偶矢末端看去，逆时针转动
为正。
20
空间力偶矩是自由矢量，它有三个要素：
力系向点简化.avi
26
若取简化中心O点为坐标原点，则：
2 2 2 Fix FR Fiy Fiz FRy FRx FRz 主矢方向 cos , cos b , cosg FR FR FR 根据力对点之矩与力对轴之矩的关系: [ mO ( Fi ) ] x m x ( Fi ) mOx ; mOy [ mO ( F ) ] y m y ( F ); mOz [ mO ( F ) ] z m z ( F )

第三章 空间力系

M y (F) M y (Fx ) M y (Fy ) M y (Fz ) Fx z Fz x Mz (F) Fy x Fx y
MO (F)x yFz zFy M x (F ) MO (F ) y zFx xFz M y (F )
MO (F)z xFy yFx M z (F)
1)力 F 的大小为 F Fx2 Fy2 Fz2 5 2 kN
2)力 F 的方向余弦以及与坐标轴的夹角为
cos F ,i 3 0.424; F ,i θ 64.9 52
cos F , j 4 0.566 ; F , j β 55.55 52
cos F ,k 5 0.707 ; F ,k γ 180 45 135 52
Fx F cos , Fy F cos , Fz F cos (3 1)
5
第三章 空间力系
§3-1 空间汇交力系 2）二次投影法（间接投影法）
当力与轴Ox，Oy正向夹角不易确定 时，可先将 F 投影到坐标平面xy上，得 Fxy，再将Fxy投影到x,y轴上，于是投影 的大小为：
Fx Fxy cos F sing cos Fy Fxy sin F sing sin
x
解：由题知：
Fx 4.5kN ;Fy 6.3kN ;Fz 18kN
y Fy
β γ
\力F 的大小
Fz
F Fx2 Fy2 Fz2 19.6 kN
zF
力F 的方向余弦，及与坐标轴的夹角为
cos Fx 4.5 0.220， 76.7
F 19.6
cos Fy 6.3 0.322, 71.1
侧面 风力
b
(a)图为空间汇交力系；(b)图为空间任意力系 (b)图中去了风力为空间平行力系。

空间力系分解课件

定性。
科学研究
在物理、化学、生物等领域中，需 要进行空间力系的解析分解，以研 究受力对物质运动和变化的影响。
日常生活
在日常生活中，许多设备和工具都 需要考虑力的作用和影响，如车辆 、家具、玩具等，因此也需要进行 空间力系的解析分解。
04
CATALOGUE
空间力系分解的实例分析来自实例一：斜拉桥的受力分析
平衡法
根据力的平衡条件，将空 间力系分解为若干个平衡 的子力系，然后分别进行 分析。
02
CATALOGUE
空间力系的几何分解
空间力系的几何表示
空间力系
在三维空间中，力系是由多个力矢量组成的系统。这些力矢量具有大小、方向 和作用点，并且遵循牛顿第三定律。
几何表示
空间力系可以用矢量图来表示，其中每个力矢量由一个箭头表示，箭头的长度 代表力的大小，箭头的指向代表力的方向，箭头的起点代表力的作用点。
在空间力系分解时，需要明确力的方向， 以确保分力是唯一的。
力系分解的发展趋势与展望
智能化与自动化
随着人工智能和机器学习技术的发展，未来空间力系分解将更加智能 化和自动化，能够自动识别和选择最佳的分解方法。
多学科交叉融合
空间力系分解将进一步与数学、物理、工程等多个学科交叉融合，推 动相关领域的发展。
空间力系
在三维空间中，力系由三个互相垂直 的主矢和三个互相垂直的主矩组成， 主矢描述力的大小和方向，主矩描述 力矩的大小和方向。
力系分解的意义
01
02
03
简化问题
通过将复杂的力系分解为 简单、易于处理的子力系 ，可以简化问题的分析和 计算。
便于分析
分解后的力系可以更好地 揭示力的作用效果和相互 关系，便于对问题进行深 入分析。

第3章空间力系简


二、 空间任意力系的平衡方程
空间任意力系平衡的充要条件：该力系的主矢、主矩分别为零. 空间任意力系的平衡方程
∑F
x
=0
∑F
y
=0
∑F
z
=0
∑M
x
=0
∑M
y
=0
∑M
z
=0
空间平行力系的平衡方程
∑F =0 ∑M =0 ∑M =0
z x y
重为G的均质正方形板置于水平面内 求球铰链O和蝶铰 例:重为 的均质正方形板置于水平面内 求球铰链 和蝶铰 重为 的均质正方形板置于水平面内,求球铰链 处的反力及绳的拉力. 链A处的反力及绳的拉力 处的反力及绳的拉力 z B
即：合力等于各分力的矢量和 2、解析法： 、解析法 由于 Fi = X ii + Y i j + Z i k 合力 代入上式
i
R = ∑ X i i + ∑Y i j + ∑ Z i k
∴
由 ∑ X i 为合力在x轴的投影，
Rx = ∑ X i R y = ∑Y i Rz = ∑Z i
3、合力投影定理： 、合力投影定理 空间力系的合力在任一轴上的投影，等于各分力在同一轴 上投影的代数和。
Mx = ∑Mix = −M3 − M4 cos 45 − M5 cos 45 = −193.1N⋅ m My = ∑Miy = −M2 = −80N⋅ m
Mz = ∑Miz = −M1 − M4 cos 45 − M5 cos 45 = −193.1N⋅ m
例4-11 已知：正方体上作用两个力偶
S1
S5= S1= -P/2
2 2 2 合力: R = R x + R y + R z = ( ∑ X ) 2 + ( ∑Y ) 2 + ( ∑ Z ) 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
问题：如果已知： 如何求力F 对 z 轴之矩 F Fx i Fy j Fz k z Fz
F k i x
Fy Fxy
力对轴之矩计算公式
Fx
j y Fx
z x
M x ( F ) yFz zFy Fy y M y ( F ) zFx xFz
F F1 F2
F1
F2
r
M1 M2
F1'
F2'
F
'
F ' F1' F2'
M R {F , F ' }
M R r F ' r (F1 'F2 ' ) r F1 'r F2 ' M1 M2
rDC
C
F2
F1 '
M1 rBA F1
F2 '
M 2 rDC F2
rBA F1 M1 M 2 rDC F2
基本量的计算
二、力偶的性质
性质一 力偶不能与一个力等效 {F , F '} {FR } 性质二 力偶可在其作用面内任意移动（或移到另一平行平 面),而不改变对刚体的作用效应
Fxy
M z ( F ) xFy yFx
问题：力对轴之矩与力对点之矩有什么关系？
基本量的计算
力对轴之矩
MO
O
z F
M x ( F ) yFz zFy M y ( F ) zFx xFz M z ( F ) xFy yFx
力对点之矩在各坐标轴上的投影
x
y r
M Ox yFz zFy M Oy zFx xFz M Oz xFy yFx
M x ( F ) M Ox M y ( F ) M Oy M z ( F ) M Oz
结论:力对轴之矩等于力对轴上任意一点之矩在该轴上的投影
2.2力对轴之矩
物体绕轴转动效果的度量。 以门绕Z轴的转动为例来讨论。 显然有：Mz(F1)=0； Mz(F2)=0 将力F分解成Fz和Fxy，可见 Mz(Fz)=0; Mz(Fxy)=MO(Fxy)
O
z
Fz
h
F Fxy
y
x
力与轴相交或平行，对轴之矩为零
F1
F2
故力F对轴z之矩可写为：Mz(F)=MO(Fxy)=Fxyh 力F对轴z之矩Mz(F)等于力在垂直于z轴之平面 内的分量Fxy对轴z与该平面交点O之矩。 正负用右手螺旋法确定，（图中为正）。
Fz
B F Fy Fxy D y A
Fxy Fx、Fy；
显然有： F=Fx+Fy+Fz；
Fx
z x
K
′ 且各分力为： Fx F cos cos F cosBAE Fx 由定义知后者正是力 在各轴上的投影。故 Fy F cos sin F cos BAK Fy 正交坐标系中，投影 Fz F sin F cos F cosBAC Fz 和分力大小相等。
4、空间一般力系:若作用于物体上所有的力（包括力偶） 都不在同一平面内，则力系称为空间一般（任意）力系。
基本量的计算
基本量的计算包括：
(1) 力在轴上的投影； (2) 力对点之矩与力对轴之矩；
(3) 力偶。
基本量的计算
1. 力在空间坐标轴上的投影 力F 为Fz、Fxy；
z E y x C A o
利用合力矩定理，进一步有：
Mz(F)=Mz(Fx)+Mz(Fy)+Mz(Fz)=Fyx－ Fxy
例: 试写出图中力F在轴上的投影及对力轴之矩。
Fx=0
Fy=(4/5)F=40 N FZ=(3/5)F=30 N Mx(F)=-Fyz+Fzy =-40+36=-4 N.m
z a=0.6m a
b=0.8m B
F F
x
F
a a
F F
a a a
a
A
B
F
a
x
F F
A
F F
B
基本量的计算
性质三 只要力偶矩矢量的方向和大小不变（F，d 可变）， 则力偶对刚体的作用效应就不变。
FF 2
A
F
a a a
B
F
F 2
基本量的计算
三、力偶系的合成
设作用于刚体上的两个力偶 M1 , M 2
M1 {F1 , F1' } M 2 {F2 , F2' }
a
O A
FZ
F=50N
z=1m Fy C x=0.2m
y
My(F)=-FZx=-6 N.m
Mz(F)=Fyx=8 N.m
A' x y=1.2m
3、力偶的矢量表示
3.1 力偶矩矢：
空间力偶对刚体的作用效果取决于 力偶矩的大小； 力偶作用平面； 力偶的转动方向。
y
x
F
M
F'
z
力偶矩矢 M：矢的长度--力偶矩的大小； 矢的指向--力偶作用平面的法向； 转向--由右手螺旋规则确定。
故：力偶对刚体的作用完全由力偶矩矢所确定。 力偶矩矢是自由矢，可平行移动。 空间力偶系的合成可按力偶矩矢量求和进行。
基本量的计算
3.2、力偶的等效条件和性质
一、力偶的等效条件(定理）
{F1 , F1'} {F2 , F2' }
•两个力偶等效的条件是它们的力偶矩相等 M1 M2 B
rBA
A
F1
D
第三章 空间力系
3.1
3.2 3.3 3.4
基本量的计算
空间力系简化 平衡条件和平衡方程
空间力系平衡问题
空间力系实例
车 床 主 轴
手摇钻
飞行的飞机
空间力系的分类
空间力系
-各力作用线不共面的力系
1、空间汇交力系:各力作用线汇交于同一点(不含力偶)。 2、空间力偶系:若物体上仅仅有力偶的作用，并且它们都 不在同一平面内。 3、空间平行力系:各力作用线相互平行(可包含力偶)。
z F
d
y
r
基本量的计算
(2) 解析表示式
r xi yj zk F Fx i Fy j Fz k
MO r F
z
Fz
F
k
k z Fz
r j y
z
Fy
x
y
i x Fx
j y Fy
x
i
Fx
M oxi M oy j M oz k
力对点之矩在轴上的投影：
M Ox yFz zFy M Oy zFx xFz M xF yF y x Oz
二次投影法：先投影到坐标面，再投影到轴上。
基本量的计算
2.1、力对点之矩
1、力对点之矩的数学描述 (1) 矢量表示式
MO r F
M O Fd
力对点之矩三要素: (1) 大小: 力F与力臂的乘积 (2) 方向: 转动方向(逆为正,顺为负) (3) 作用面: 力矢与矩心构成的平面
MO
O x