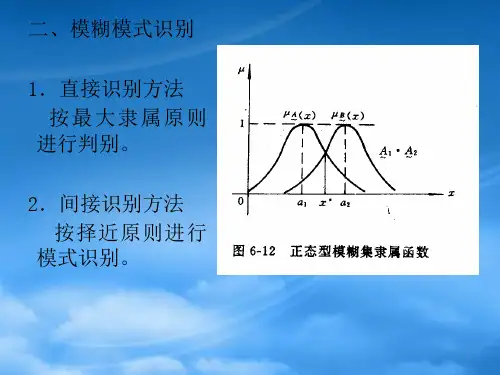
第二节 模糊模式识别

模糊模式识别1 模糊模式识别的原则(1) 最大隶属原则当模式是模糊的，被识别对象是明确的，问题可以描述如下：设有n 个模式，它们分别表示成某论域X （X 可以是多个集合的笛卡儿乘积集）的n 个模糊子集12,,,n A A A，而0x X ∈是一个具体被识别的对象，若有},2,1{n i ∈，使得12()m ax{(),(),,()}inA o A o A o A o x x x x μμμμ=则认为0x 相对属于模式i A。

对事物进行直接识别时，所依据的是最大隶属原则。

这种方法适合处理具有如下特点的问题：a 用作比较的模式是模糊的；b 被识别的对象本身是确定的。

(2) 贴近度原则当模式及被识别对象都是模糊的，问题可以描述如下：设论域X 的模糊子集12,,,n A A A代表n 个模糊模式，被识别的对象可以表示成X 的子集B，若有},2,1{n i ∈，使得12(,)max{(,),(,),,(,)}i n B A B A B A B A σσσσ=则认为B相对合于模式A。

在模糊模式识别的具体应用中，关键是模式或被识别对象的模糊集合的构造，即如何建立刻画模式或对象的模糊集合。

根据实际应用来看，通常有三种主要方法，简单模式的识别方法，语言模式的识别方法和统计模式的识别方法。

2 模糊模式识别方法（一）简单模式的模糊模式识别具体的模糊模式识别工作可分为如下三个步骤：1）选取模式的特征因子集合},,,{21n X X X =X，被识别的对象表示为nni i XXX X ⨯⨯⨯∆∏= 211上的向量（),,,21n x x x ，,1,2,,,i i x X i n ∈= 或者表示为∏=ni i X 1上的模糊子集；2）建立模糊模式的隶属函数()A X μ,1()ni i A F X =∈∏；3）利用最大隶属度原则或贴近度原则对被识别的对象进行归属判决。

特征因子(1,2,,)i X i n = 的选取直接影响识别的效果，它取决于识别者的知识和技巧，很难做一般性讨论，而模式识别中最困难的是建立模式的隶属函数，人们还没有从理论上彻底解决隶属函数的确定问题。

模糊模式识别1模糊数学基本理论9.1 模糊集合•模糊"一词来自英文fuzzy，意思是"模糊的"、"（形状或轮廓）不淸楚"等等.•模糊数学是运用数学方法研究和处理带有模糊性现象的一门新兴学科，它的创始人是美国加利福尼亚大学著名的控制论专家扎德(L.A.zadah)•所谓的模糊性，是指事物的亦此亦彼性，反映在概念形成过程中外延的不分明性•1965年，美国加利福尼亚大学控制论专家扎德（L, A. Zadeh〉教授在《信息与控制》杂志上发表了一箱开创性论文《模糊集》，这标志着模糊数学的诞生。

•在人类社会和各个科学领域中，人们所遇到的各种量大体上可以分成两大类：•确定性的与不确定性的，而不确定性又可分为随机性和模糊性.人们正是用三种数学来分别研究客观世界中不同的量，即在这种框架内，数学模型分为三大类.•第一类是确定性数学模型。

这类模型研究的对象具有确定性，对象之间具有必然的关系，最典型的就是用微分法、微分方程、差分方程所建立的数学模型.•第二类是随机性数学模型。

这类模型研究的对象具有随机性，对象之间具有偶然的关系，如用概率分布方法、马尔可夫(Markov〉链所建立的数学模型。

•第三类是模糊性数学模型。

这类模型所研究的对象与对象之间的关系具有模糊性.两种不确定性之间的区别：•随机性的不确定性，也就是概率的不确定性。

例如，“明天有雨”，“掷一骰子出现6点”等，它们的发生是一种偶然现象，具有不确定性.•在这里，事件本身是确定的，而事件的发生不确定。

只要时间过去，到了明天，“明天有雨”是否发生就变成确定的了。

“掷一骰子出现6点”，只要实际做一次实验，它就变成确定的了.•而模糊性的不确定性，即使时间过去了，或者实际做了一次实验，它们仍然是不确定的。

这主要是因为事件本身( 如“青年人”、“高个子”等) 是不确定的，具有模糊性，是由概念、语言的模糊性产生的。

模糊数学在实际中的应用•几乎涉及国民经济的各个领域，尤其在科学技术、经济管理、社会科学方面得到了广泛而又成功的应用.比如：•在生物学发展史上，由于科学技术的不断进步，人们发现在动物与植物之间存在着“中介状态”，于是又分出张将生物分为五类、六类.这一现象用模糊集合就可得到合理的解释.•对某个领域的经济发展水平的评价，往往划分为富裕型、小康型、温饱型、贫困型，这些都是模糊的，只有通过模糊数学模型才能得到合乎实际的评价。

绪言任何新生事物的产生和发展，都要经过一个由弱到强，逐步成长壮大的过程，一种新理论、一种新学科的问世，往往一开始会受到许多人的怀疑甚至否定。

模糊数学自1965年L.A.Zadeh教授开创以来所走过的道路，充分证实了这一点，然而，实践是检验真理的标准，模糊数学在理论和实际应用两方面同时取得的巨大成果，不仅消除了人们的疑虑，而且使模糊数学在科学领域中，占有了自己的一席之地。

经典数学是适应力学、天文、物理、化学这类学科的需要而发展起来的，不可能不带有这些学科固有的局限性。

这些学科考察的对象，都是无生命的机械系统，大都是界限分明的清晰事物，允许人们作出非此即彼的判断，进行精确的测量，因而适于用精确方法描述和处理。

而那些难以用经典数学实现定量化的学科，特别是有关生命现象、社会现象的学科，研究的对象大多是没有明确界限的模糊事物，不允许作出非此即彼的断言，不能进行精确的测量。

清晰事物的有关参量可以精确测定，能够建立起精确的数学模型。

模糊事物无法获得必要的精确数据，不能按精确方法建立数学模型。

实践证明，对于不同质的矛盾，只有用不同质的方法才能解决。

传统方法用于力学系统高度有效，但用于对人类行为起重要作用的系统，就显得太精确了，以致于很难达到甚至无法达到。

精确方法的逻辑基础是传统的二值逻辑，即要求符合非此即彼的排中律，这对于处理清晰事物是适用的。

但用于处理模糊性事物时，就会产生逻辑悖论。

如判断企业经济效益的好坏时，用“年利税在100万元以上者为经济效益好的企业” 表达，否则，便是经济效益不好的企业。

根据常识，显而易见：“比经济效益好的企业年利税少1元的企业，仍是经济效益好的企业”，而不应被划为经济效益不好的企业。

这样，从上面的两个结论出发，反复运用经典的二值逻辑，我们最后就会得到，“年利税为0者仍为经济效益好的企业”的悖论。

类似的悖论有许多，历史上最著名的有“罗素悖论”。

它们都是在用二值逻辑来处理模糊性事物时产生的。

4 模式识别技术一个模式类是由一些给定的共同属性所决定的一个类别，该类别中的一员就是一个模式。

所谓模式识别也就是对所研究的对象根据其共同特征或属性进行识别和分类。

严格地说，模式识别不是简单的分类学。

模式识别过程主要包括三部分，首先从观测样品中提取特征；然后按照某种原则对这些特征进行选择，保留一些起主要作用的特征用于识别；最后采用各种判别方法或聚类方法，根据多个特征对样品进行研究和分类。

模式识别的方法很多，本章讨论了模糊综合评判、模糊模式识别、分段线性模式识别和人工神经网络模式识别等四种方法。

4.1 模糊综合评判法模糊综合评判就是应用模糊变换原理和最大隶属度原则，考虑与被评价事物相关的各个因素，对其所做的综合评判。

在模糊综合评判中需考虑两个集合，即着眼因素集合),,,(21m u u u U =和抉择评语集合),,,(21n v v v V =。

做模糊综合评判的关键就在于找出着眼因素集合U 与抉择评语集合V 之间的模糊关系，并确定合适的综合评判模型。

对于断层识别而言，通过分析地震属性参数与小断层之间的模糊关系，建立各种地震属性参数对应小断层的隶属函数，最后预测小断层存在的肯定区、可能区及否定区。

首先对着眼因素集U 中的单因素),,2,1(m i u i =做单因素评价，从因素i u 着眼确定该事物对抉择等级),,2,1(n j v j =的隶属度ij r ，这样就得出第i 个因素i u 的单因素评价集),,,(21in i i i r r r r =它是抉择评语集合上的模糊子集。

这样m 个着眼因素的评价集就构造出一个总的评价矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=mn m m n n r r r r r r r r r R 212222111211 (4-1) 式中 R ——着眼因素集U 到抉择评语集V 的一个模糊关系；ij r ——因素i u 对抉择等级j v 的隶属度。

在多因素综合评价中，一方面，对于被评价的事物，从不同的因素着眼可以得到不同的结论；另一方面，在诸多着眼因素中，有些因素在总评价中影响程度大些，而另一些可能影响小些，但究竟多大，则是一个模糊择优问题。

模式识别是人工智能的一个重要应用领域，其方法主要包括以下几种：
统计模式识别：基于统计原理，利用计算机对样本进行分类。

主要方法有基于概率密度函数的方法和基于距离度量的方法。

结构模式识别：通过对基本单元（如字母、汉字笔画等）进行判断，是否符合某种规则来进行分类。

这种方法通常用于识别具有明显结构特征的文字、图像等。

模糊模式识别：利用模糊集合理论对图像进行分类。

这种方法能够处理图像中的模糊性和不确定性，提高分类的准确性。

人工神经网络：模拟人脑神经元的工作原理，通过训练和学习进行模式识别。

常见的神经网络模型有卷积神经网络（CNN）、循环神经网络（RNN）等。

支持向量机（SVM）：通过找到能够将不同分类的样本点最大化分隔的决策边界来进行分类。

SVM在处理高维数据和解决非线性问题时具有较好的性能。

决策树：通过树形结构对特征进行选择和分类。

决策树可以直观地表示分类的决策过程，但易出现过拟合问题。

集成学习：通过构建多个弱分类器，并将其组合以获得更强的分类性能。

常见的集成学习方法有bagging、boosting等。

在实际应用中，根据具体任务的需求和数据特点，可以选择适合的模式识别方法。

同时，也可以结合多种方法进行综合分类，以提高分类的准确性和稳定性。

三角形类型的模糊模式识别摘要：三角形类型的模糊模式识别问题，在生物细胞染色体形状的识别、癌细胞以及白血球分类等问题中有很大意义。

发现传统方法和参考论文所提出的新方法在某些三角形判断中的不足，故提出基于给定阈值5.0=λ的最大隶属度原则，提出关于三角形角度的指数型隶属度函数，并与其它两种方法进行对比，结果表明指数函数性质使所求得的隶属度差距较大、区别明显，便于识别，并且更贴近于人们的直观理解，能更好的实现三角形的分类。

关键词：三角形；最大隶属度原则；阀值原则；指数型隶属度函数1、基本概念a) 最大隶属度原则：当模式是模糊的，被识别对象时明确的，问题可以描述成：设~~2~1,...,,n A A A 是论域U 中的n 个模糊模式。

0U 是U 中一个元素。

若有},...,2,1{n i ∈，使：()()}{m ax 010~~u u j i A nj A μμ≤≤=则认为0U 相对隶属于模式~i A ，并称这种识别方法为最大隶属度原则。

b) 阀值原则：设~~2~1,...,,n A A A 是论域U 中的n 个模糊模式，规定一个阀值](1,0∈λ，U u ∈为一个待识别对象。

若()()()λ<},...,,m ax {~~2~1u A u A u A n ，则作为“拒绝识别”的判断；若()()()λ≥},...,,m ax {~~2~1u A u A u A n ，并且有k 个模式()()()u A u A u A ik i i ~~2~1,...,,大于或等于λ，则认为识别可行。

2、指数型隶属度函数的建立设三角形的三个内角分别为C B A ,,，并且约定0>≥≥C B A 。

取特征因子集()}0,180,,{>≥≥=++=C B A C B A C B A U ο。

根据三角形的特征，在U 中规定5个具体的三角形：等腰三角形~I ；直角三角形~R ；等边三角形~E ；等腰直角三角形~IR ；非典型三角形~O 。

第一部分模糊计算课后任务找一些使用模糊数学作为基础的实际应用，并归类整理。

对每种实际应用进行简单介绍，并形成文档。

模糊数学的应用1、模糊模式识别2、模糊聚类分析3、模糊综合评价4、模糊控制系统5、模糊数学在决策中的应用1、模糊模式识别模式识别就是机器的识别，目的在于让机器自动识别事物。

一个典型的模式识别系统，由数据获取、预处理、特征提取和选择、分类决策以及分类器组成。

一般分为学习过程和识别过程，通过这两个过程对未知类别进行分类。

在生活中有些模式的界限是不明确的，所以对于界限不明确的模式识别就称为模糊模式识别。

模糊模式识别主要分为三个步骤：（1）、提取特征（2）、建立标准类型模型（3）、建立识别判决准则例如：医疗诊断问题，通过病人的症状对病人进行诊断。

设病人集合为P={p1,p2,p3,p4},症状结合X={x1(发烧),x2(头痛),x3(胃疼),x4(咳嗽),x5(胸痛)},诊断结论的集合D={A1(病毒性感冒),A2(疟疾),A3(伤寒),A4(胃病),A5(胸部问题)}。

通过专家经验数据，可以得到症状与诊断结果的关系，然后通过数据关系建立症状与诊断结果的标准模型，最后经过判别准则对新的病人进行诊断。

这里判别准则大致有以下几种，最大隶属度原则、阈值原则、折近原则等等。

2、模糊聚类分析“聚类”就是按照一定的要求和规律对事物进行区分和分类，传统的聚类分析是一种硬划分，他把每个待分类的对象严格的划分到某类中，即划分界限是明确的。

生活中对象大多数都没有明确的界限划分，所以，需要利用模糊集的理论来对对象进行分类，这种聚类分析叫做模糊聚类分析。

常用的模糊聚类分析大致分为两类，其一是基于模糊关系（矩阵）的聚类分析，其二是基于目标函数的聚类分析。

基于模糊关系的聚类分析：即利用模糊集合之间的相似程度来对对象进行分类，大致步骤为：（1）、数据规格化（2）、构造模糊相似矩阵（3）、模糊分类数据规格化的方法有：（1）标准化方法（2）均值规格化方法（3）中心规格化方法（4）最大值规格化方法相似矩阵的构造方法（1）数量积法（2）夹角余弦法（3）相关系数法（4）距离法（5）绝对值倒数法（6）主观评定法模糊分类方法（1）利用模糊传递闭包进行模糊分类（2）直接聚类法（3）最大树聚类法（4）编网聚类法基于目标函数的聚类分析：基于目标函数的模糊聚类方法是把聚类归结成一个带约束的线性规划问题，通过优化求解得数据集的模糊划分和聚类。

《模糊数学》教学大纲课程编号：121082B课程类型：□通识教育必修课□通识教育选修课□专业必修课□√专业选修课□学科基础课总学时：32 讲课学时：32 实验（上机）学时：0学分：2适用对象：金融数学专业先修课程：数学分析、高等代数、概率论与数理统计毕业要求：1.掌握数学、统计及计算机的基本理论和方法2.具备国际视野，能够与同行及社会公众进行有效沟通和交流一、教学目标模糊数学是统计学院金融数学专业选修的基础课之一。

通过本课程的学习，使学生对模糊数学的原理和思想方法有一个基本的认识。

掌握应用模糊数学的原理分析和解题的基本技巧。

了解模糊数学方法在各个领域的应用，为应用模糊数学知识解决问题打下基础。

二、教学基本要求本课以课堂讲授为主。

适当补充一些模糊数学在实际中应用的实例，理论联系实际。

在各章中均可安排一些内容引导学生自学，通过布置作业和讨论题，提高学生自己解决问题与分析问题的能力。

同时，也可适当让学生自己来寻找一些实际问题，应用学过的知识来进行分析、综合、评判，以期达到更好的巩固、应用的目的。

(一) 模糊数学的基本理论和基本原理1、模糊集合是处理模糊事物的新的数学概念，是模糊数学的基础。

理解模糊集的定义、表示方法、模糊集的运算。

了解模糊算子的定义及各种模糊算子，了解模糊集的模糊度定义。

2、理解模糊集截集的定义及性质，掌握模糊数学的基本原理：分解定理（联系普通集与模糊集的桥梁）、扩张原理。

了解模糊数及模糊数的运算。

(二) 模糊数学方法及其在各领域中的应用1、理解模糊关系的概念及性质，深入理解在有限域的情况下，模糊关系可以用矩阵表示。

理解模糊关系合成的定义及性质。

理解掌握贴近度概念及最大隶属原则和择近原则。

了解模糊变换以及模糊控制。

2、对于模糊数学方法的应用。

重点掌握模糊模式识别、模糊聚类分析、模糊综合评判决策，以及了解它们在不同领域的应用举例。

每章节后的习题要求全部完成；本课程建议使用形成性和终结性考试相结合，并各占50%比例。