模糊模式识别的方法

模糊模式识别1 模糊模式识别的原则(1) 最大隶属原则当模式是模糊的，被识别对象是明确的，问题可以描述如下：设有n 个模式，它们分别表示成某论域X （X 可以是多个集合的笛卡儿乘积集）的n 个模糊子集12,,,n A A A，而0x X ∈是一个具体被识别的对象，若有},2,1{n i ∈，使得12()m ax{(),(),,()}inA o A o A o A o x x x x μμμμ=则认为0x 相对属于模式i A。

对事物进行直接识别时，所依据的是最大隶属原则。

这种方法适合处理具有如下特点的问题：a 用作比较的模式是模糊的；b 被识别的对象本身是确定的。

(2) 贴近度原则当模式及被识别对象都是模糊的，问题可以描述如下：设论域X 的模糊子集12,,,n A A A代表n 个模糊模式，被识别的对象可以表示成X 的子集B，若有},2,1{n i ∈，使得12(,)max{(,),(,),,(,)}i n B A B A B A B A σσσσ=则认为B相对合于模式A。

在模糊模式识别的具体应用中，关键是模式或被识别对象的模糊集合的构造，即如何建立刻画模式或对象的模糊集合。

根据实际应用来看，通常有三种主要方法，简单模式的识别方法，语言模式的识别方法和统计模式的识别方法。

2 模糊模式识别方法（一）简单模式的模糊模式识别具体的模糊模式识别工作可分为如下三个步骤：1）选取模式的特征因子集合},,,{21n X X X =X，被识别的对象表示为nni i XXX X ⨯⨯⨯∆∏= 211上的向量（),,,21n x x x ，,1,2,,,i i x X i n ∈= 或者表示为∏=ni i X 1上的模糊子集；2）建立模糊模式的隶属函数()A X μ,1()ni i A F X =∈∏；3）利用最大隶属度原则或贴近度原则对被识别的对象进行归属判决。

特征因子(1,2,,)i X i n = 的选取直接影响识别的效果，它取决于识别者的知识和技巧，很难做一般性讨论，而模式识别中最困难的是建立模式的隶属函数，人们还没有从理论上彻底解决隶属函数的确定问题。

模糊数学第1节模糊聚类分析第2节模糊模式识别第3节模糊相似优先比方法第4节模糊综合评判第5节模糊关系方程求解在自然科学或社会科学研究中,存在着许多定义不很严格或者说具有模糊性的概念。

这里所谓的模糊性，主要是指客观事物的差异在中间过渡中的不分明性，如某一生态条件对某种害虫、某种作物的存活或适应性可以评价为“有利、比较有利、不那么有利、不利”；灾害性霜冻气候对农业产量的影响程度为“较重、严重、很严重”，等等。

这些通常是本来就属于模糊的概念，为处理分析这些“模糊”概念的数据，便产生了模糊集合论。

根据集合论的要求，一个对象对应于一个集合，要么属于，要么不属于，二者必居其一，且仅居其一。

这样的集合论本身并无法处理具体的模糊概念。

为处理这些模糊概念而进行的种种努力，催生了模糊数学。

模糊数学的理论基础是模糊集。

模糊集的理论是1965年美国自动控制专家查德(L. A. Zadeh)教授首先提出来的，近10多年来发展很快。

模糊集合论的提出虽然较晚，但目前在各个领域的应用十分广泛。

实践证明，模糊数学在农业中主要用于病虫测报、种植区划、品种选育等方面，在图像识别、天气预报、地质地震、交通运输、医疗诊断、信息控制、人工智能等诸多领域的应用也已初见成效。

从该学科的发展趋势来看，它具有极其强大的生命力和渗透力。

在侧重于应用的模糊数学分析中，经常应用到聚类分析、模式识别和综合评判等方法。

在DPS系统中，我们将模糊数学的分析方法与一般常规统计方法区别开来，列专章介绍其分析原理及系统设计的有关功能模块程序的操作要领，供用户参考和使用。

第1节模糊聚类分析1. 模糊集的概念对于一个普通的集合A，空间中任一元素x，要么x∈A，要么x∉A，二者必居其一。

这一特征可用一个函数表示为：A x x A x A()=∈∉⎧⎨⎩1A(x)即为集合A的特征函数。

将特征函数推广到模糊集，在普通集合中只取0、1两值推广到模糊集中为[0, 1]区间。

定义1 设X为全域，若A为X上取值[0, 1]的一个函数，则称A为模糊集。

第6讲模糊模式识别（第三章模糊模式识别）一、模式识别一般原理1.模式识别的概念模式识别是人工智能的一个重要方面，也是一门独立的学科。

模式：用数学描述的信息结构或观察信号。

模式识别就是把要辨别的对象，通过与已知模式进行比较，从而确定出它和哪一个模式相类同的过程。

2.模式识别系统人们识别事物时，首先要对事物进行观察，抓住特点，分析比较，才能加以判断和辨别，而机器进行模式识别也同样要有这些过程。

因此模式识别系统通常由以下四个部分构成：①传感器部分：这是获取信息的过程。

比如摄像头就象人的眼睛，把图像信息变为电信号，麦克风象人的耳朵，获取声音信号，又如霍尔元件可以感受磁场，压电陶瓷可以把力转换为电信号等等。

②预处理部分：这是对信息进行前端处理的过程。

它把传感器送来的信号滤除杂波并作规范化、数字化。

③特征提取部分：这是从信号中提取一些能够反映模式特征的数据的过程。

④识别判断部分：这是根据提取的特征，按照某种归类原则，对输入的模式进行判断的过程。

二、模糊模式识别模糊模式识别主要是指用模糊集合表示标准模式，进而进行识别的理论和方法。

主要涉及到三个问题：（1）用模糊集合表示标准模式；（2）度量模糊集合之间的相似性；（3）模糊模式识别的原则。

例3.1 邮政编码识别问题识别：0，1，2，……，9关键：1）如何刻化，0，1，……，9（如何选取特征？）（区分）2）如何度量特征之间的相似性？ 1．模糊集合的贴近度贴近度是度量两个模糊集合接近（相似）程度的数量指标，公理化定义如下：定义3.1 设,,()A B C F X ∈，若映射[]:()()0,1N F X F X ⨯→ 满足条件：①(,)(,)N A B N B A =； ②(,)1,(,)0N A A N X φ==； ③若A B C ⊆⊆，则(,)(,)(,)N A C N A B N B C ≤∧。

则称(,)N A B 为模糊集合A 与B 的贴近度。

N 称为()F X 上的贴近度函数。

第九章模糊识别技术模式识别（Pattern Recognition）是本世纪六十年代初迅速发展起来的、与高技术的研究开发有着密切联系的一门新兴学科，是人工智能的重要组成部分。

从本质上讲，模式识别所讨论的的核心问题便是如何使机器模拟人脑的思维方法，来对客观事物进行有效地识别和分类，因此，模式识别又经常被称作模式分类（Pattern Classification）。

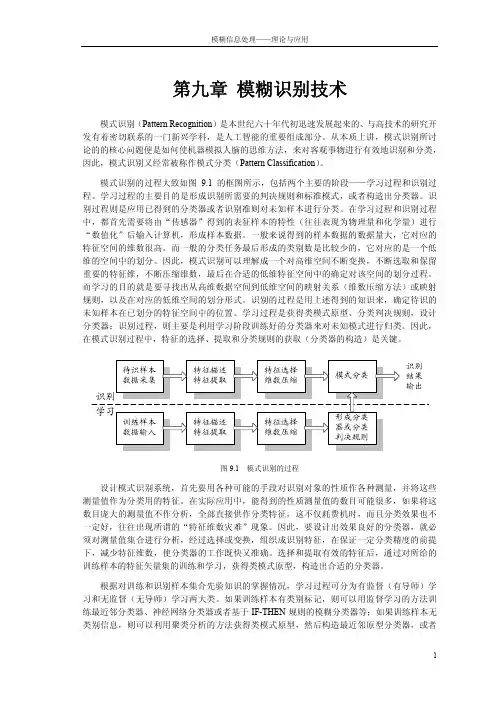
模式识别的过程大致如图9.1的框图所示，包括两个主要的阶段——学习过程和识别过程。

学习过程的主要目的是形成识别所需要的判决规则和标准模式，或者构造出分类器。

识别过程则是应用已得到的分类器或者识别准则对未知样本进行分类。

在学习过程和识别过程中，都首先需要将由“传感器”得到的表征样本的特性（往往表现为物理量和化学量）进行“数值化”后输入计算机，形成样本数据。

一般来说得到的样本数据的数据量大，它对应的特征空间的维数很高。

而一般的分类任务最后形成的类别数是比较少的，它对应的是一个低维的空间中的划分。

因此，模式识别可以理解成一个对高维空间不断变换，不断选取和保留重要的特征维，不断压缩维数，最后在合适的低维特征空间中的确定对该空间的划分过程。

而学习的目的就是要寻找出从高维数据空间到低维空间的映射关系（维数压缩方法）或映射规则，以及在对应的低维空间的划分形式。

识别的过程是用上述得到的知识来，确定待识的未知样本在已划分的特征空间中的位置。

学习过程是获得类模式原型、分类判决规则，设计分类器；识别过程，则主要是利用学习阶段训练好的分类器来对未知模式进行归类。

因此，在模式识别过程中，特征的选择、提取和分类规则的获取（分类器的构造）是关键。

图9.1 模式识别的过程设计模式识别系统，首先要用各种可能的手段对识别对象的性质作各种测量，并将这些测量值作为分类用的特征。

在实际应用中，能得到的性质测量值的数目可能很多，如果将这数目庞大的测量值不作分析，全部直接供作分类特征，这不仅耗费机时，而且分类效果也不一定好，往往出现所谓的“特征维数灾难”现象。

三角形类型的模糊模式识别摘要：三角形类型的模糊模式识别问题，在生物细胞染色体形状的识别、癌细胞以及白血球分类等问题中有很大意义。

发现传统方法和参考论文所提出的新方法在某些三角形判断中的不足，故提出基于给定阈值5.0=λ的最大隶属度原则，提出关于三角形角度的指数型隶属度函数，并与其它两种方法进行对比，结果表明指数函数性质使所求得的隶属度差距较大、区别明显，便于识别，并且更贴近于人们的直观理解，能更好的实现三角形的分类。

关键词：三角形；最大隶属度原则；阀值原则；指数型隶属度函数1、基本概念a) 最大隶属度原则：当模式是模糊的，被识别对象时明确的，问题可以描述成：设~~2~1,...,,n A A A 是论域U 中的n 个模糊模式。

0U 是U 中一个元素。

若有},...,2,1{n i ∈，使：()()}{m ax 010~~u u j i A nj A μμ≤≤=则认为0U 相对隶属于模式~i A ，并称这种识别方法为最大隶属度原则。

b) 阀值原则：设~~2~1,...,,n A A A 是论域U 中的n 个模糊模式，规定一个阀值](1,0∈λ，U u ∈为一个待识别对象。

若()()()λ<},...,,m ax {~~2~1u A u A u A n ，则作为“拒绝识别”的判断；若()()()λ≥},...,,m ax {~~2~1u A u A u A n ，并且有k 个模式()()()u A u A u A ik i i ~~2~1,...,,大于或等于λ，则认为识别可行。

2、指数型隶属度函数的建立设三角形的三个内角分别为C B A ,,，并且约定0>≥≥C B A 。

取特征因子集()}0,180,,{>≥≥=++=C B A C B A C B A U ο。

根据三角形的特征，在U 中规定5个具体的三角形：等腰三角形~I ；直角三角形~R ；等边三角形~E ；等腰直角三角形~IR ；非典型三角形~O 。