《信号与系统(第三版)习题解析》勘误表

"!#!
"#%"
"’"’’
!
$"
-%#’
!
$##&$
"
%$’#"
’
!
"%#"%
"#
’"
$!#$
%
%
’
!!!’#1
"##"#
"#"
+%$$
’’
!!
’$1
’
"
’
"#’#""$!#
"",
’"!’-!#$!’$’
"#"#""#
"#"#%"#"#"#-""&
."’"!
’’’’’’$/#’
.
!$%$!$’!$/#
’"""""#
(#/(") ’#$!#!(’) ’
!!$!判定下列信号是否为周期信号(若是周期信号’则确定信号周期,(
"!#"##%2-*3%#$
!
""*3#)2
"#"’*23%#-+()*!#
"%#%
"#$
"##"##/()#0*3
%$
#
""*-2槡#
"#’"#"#

2．脉冲编码调制（PCM） （1）脉冲调制概念 利用脉冲序列对连续信号进行抽样产生的信号称为脉冲幅度调制（PAM）信号。把连 续信号转换成数字（编码）信号进行传输或处理的调制方式称为脉冲编码调制（PCM）。PCM 通信系统的简化框图如图 5-1-2 所示。
图 5-1-2 PCM 通信系统简化框图 （2）PCM 通信特点（见表 5-1-4）
5-2 若系统函数H（jω）＝1/（jω＋1），激励为周期信号e（t）＝sin（t）＋sin（3t）， 试求响应r（t），画出e（t），r（t）波形，讨论经传输是否引起失真。
解：激励信号 e（t）＝sin（t）＋sin（3t），则 E（jω）＝F[e（t）]＝jπ[δ（ω＋1）－δ（ω－1）]＋jπ[δ（ω＋3）－δ（ω－3）]
一、系统函数 H（jω）
当且仅当 H（s）在虚轴上及右半平面无极点时，有 H ( j) H (s) s j ，也即，对于 H（s）在虚轴上有极点的系统，有 H ( j) H (s) s j 。
二、无失真传输 1．定义 系统无失真传输是指响应信号与激励信号相比，只是大小与出现的时间不同，而无波形 上的变化。 设激励信号为 e（t），响应信号为 r（t），则无失真传输的条件是 r（t）＝Ke（t－t0）， K 为常数，t0 为滞后时间，如图 5-1-1 所示。
6 / 107
圣才电子书 十万种考研考证电子书、题库视频学习平台

故响应为：
R( j) = E( j)×H ( j)
=
jπ j +
[ 1
(
+
1)
-
(
-
1)] +
jπ j +
[ 1
(
+
3)

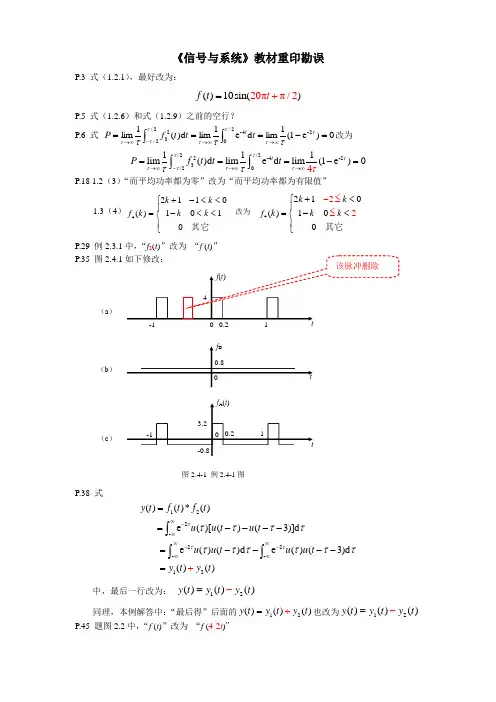
《信号与系统》教材重印勘误P.3 式（1.2.1），最好改为：()10sin(π)20π/2t f t +=P.5 式（1.2.6）和式（1.2.9）之前的空行？ P.6 式 0)e 1(1lim d e 1limd )(1lim2-2/04-2/2/23=-===∞→∞→-∞→⎰⎰ττττττττττt t t f P t改为/2/22-4-23/2111lim()d lime d lim(1e )04t P f t t t ττττττττττ-→∞→∞→∞===-=⎰⎰P.18 1.2（3）“而平均功率都为零”改为“而平均功率都为有限值”1.3（4）⎪⎩⎪⎨⎧<<-<<-+=其它01010112)(4k k k k k f 改为 4210()10202k k f k k k -≤≤+<⎧⎪=-<⎨⎪⎩其它 P.29 例2.3.1中，“f 2(t )”改为 “f (t )”P.35 图2.4.1如下修改：P.38 式122-22--12()()*()e ()[()(3)]d e ()()d e()(3)d ()()y t f t f t u u t u t u u t u u t y t y t τττττττττττττ∞-∞∞∞--∞∞==----=---+-=⎰⎰⎰中，最后一行改为：12()()()y t y t y t -=同理，本例解答中：“最后得”后面的12()()()y t y t y t +=也改为12()()()y t y t y t -=P.45 题图2.2中，“f (t )”改为 “f (4-2t )”t0.2 0 4f (t ) 图2.4-1 例2.4-1图1-1t t0.20 1-10.8 f A (t ) f D（a ）（b ）（c ）0 3.2-0.8该脉冲删除P.61 例3.4.2f 22222(2)()()*()e ()*[()(2)]e ()*()e ()*(2)11(1-e )()[1-e ](2)22t t t t t y t f t h t u t u t u t u t u t u t t u t u t ε------==--=--=--改为f 22222(2)()()*()e ()*[()(2)]e ()*()e ()*(2)11(1-e )()[1-e ](2)22t t t t t y t f t h u t u t u t u t u t u t u t t u t u t ------==--=--=--P.76 式j2π-j2πj4π-j4πj6π-j6π-j6π-j2π-j4πj2πj2πj6π1e e e e 2e e 22232111111 e e e e e e 342243()t t t t t tt t t t t tf t +++++=++++=+ 改为j2π-j2πj4π-j4πj6π-j6π-j6π-j4π-j2πj2πj4πj6πe e e e e e 1052222e 2.5e 5e 5e 2().5e e t t t t t tt t t t t tf t +++++++==+++ P.76 式（4.1.1）0011()[cos sin ]c s()22o n n n n n n A f t a n t b n t A n t A ϕ∞∞===+Ω+Ω=+Ω+∑∑改为0011()[cos sin ]cos()22n n n n n n A f t a n t b n t A n t a ϕ∞∞===+Ω+Ω=+Ω+∑∑ P.78 图4.1.3中，字母a~e 适当下移。

1. "线性调制"的一种定义是看它是否满足叠加原理(见[1],第 232 页) ,DSB 是线性调制:
m1 (t ) cos ωc t + m2 (t ) cos ωc t = [m1 (t ) + m2 (t )] cos ωc t
46 第 190 页倒 数第 3~5 行 在这个定义下,标准调幅 AM,SSB,2ASK,2PSK 都不是线性调制.但因为它门在实质上是 DSB,所以也可归类于线性调制. 注:对于 AM,用两个基带信号的和做 AM 调制结果虽然也是 AM 信号,但载波分量不是叠加关系 2.还有人将"线性调制"定义为: "调制后信号的频谱为调制信号频谱的平移及线性变换" (见[3],第 27 页) (见 3.因为"线性"一词有"成比例"的意思,故有人也把 FM 叫做线性调制,取 FM 的瞬时频偏同基带调制信号的电压成正比之意. [2],第 138 页)
V P(s1 ) p T s 1
+
∞
=∫
∞
[s1 (τ ) + nw (τ )]s1 (Tb t + τ )dτ
另外请注意其它各处 条件概率的记号
35
第 154 页 (5.3.45)式 第 158 页 (5.4.12)式
V p ( s2 ) p T s 2
P(s1 ) p(VT | s1 ) P(s2 ) p(VT | s2 )
4
33
page 第 147 页倒 数第 2 行
误 滤波器的三分贝单边带宽 B
正 滤波器的等效噪声带宽 B
备注
34 第 152 页 (5.3.27)式
∞ ∞ ∞
= ∫ r (τ )s1 (t Tb + τ )dτ =∫

《信号与系统》（第3版）习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t )表示将f ( t )波形展宽。

] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= t t i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S R S L S C题1-4图解 系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

（7）
X
z
1 2
n
u
n
u
n
10
z
n
9 n0
1 2
n
z
n
9 n0
1 2z
n
1
1 2z
1 1
10
z 0
2z
X（z）的零、极点分布图如图 8-2-1（g）所示。
（8）
8 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平

X
z
n台
1 2
圣才电子书
十万种考研考证电子书、题库视频学习平

台
第 8 章 z 变换、离散时间系统的 z 域分析
8.1 复习笔记
从本章开始陆续讨论 Z 变换的定义、性质以及它与拉氏变换、傅氏变换的联系。在此 基础上研究离散时间系统的 z 域分析，给出离散系统的系统函数与频率响应的概念。通过 本章，读者应掌握对于离散时间信号与系统的研究，是先介绍 z 变换，然后引出序列的傅 里叶变换以及离散傅里叶变换（第九章）。
4 / 75
圣才电子书
十万种考研考证电子书、题库视频学习平

台
于实轴的直线映射到 z 平面是负实轴；
（3）在 s 平面上沿虚轴移动对应于 z 平面上沿单位圆周期性旋转，每平移 ωs，则沿
单位圆转一圈。
2．z 变换与拉氏变换表达式
Z
x nT X z zesT X s Z
n
u
n
1 3
n
u
n
z
n
n
（3）
X
z
n
1 3
n
u
n
z
n
n0

3．全通函数 如果一个系统函数的极点位于左半平面，零点位于右半平面，而且零点与极点对于 jω 轴互为镜像，这种系统函数称为全通函数，此系统则称为全通系统或全通网络。它的幅频特 性是常数。
4．最小相移函数 零点仅位于左半平面或 jω轴的网络函数称为“最小相移函数”，该网络称为“最小相 移网络”。非最小相移函数可以表示为最小相移函数与全通函数的乘积，即非最小相移网络 可以用最小相移网络与全通网络的级联来代替。

（1）部分分式展开法求解
首先将 F（s）展开成部分分式之和的形式，再对各部分分式分别取逆变换后叠加即可
得出 f（t）。
（2）留数定理求解
将拉氏逆变换的积分运算转化为求被积函数 F（s）est 在围线中所有极点的留数之和。
L 1[F (s)] 1 j F (s)estds [F (s)est的留数]
1 s
s2
s 2
，故
7 / 122
圣才电子书 十万种考研考证电子书、题库视频学习平台

L
[1 cos(t)]et
s
1
s (s )2 2
；
（7） L
[t 2
2t]
d2 ds2
1 s
d ds
2 s
2 s3
2 s2
（8） L [2 (t) 3e7t ] 2 3 s7
图 子书、题库视频学习平台

二、系统函数与系统特性 1．系统函数 系统的零状态响应的拉氏变换与激励的拉氏变换之比称为系统函数，即 H（s）＝RZS （s）/E（s）。且冲激响应 h（t）↔H（s）。
2．零极点分布
H (s)

（9）e－αtsinh（βt）；
（10）cos2（Ωt）；

第1章绪论
1.1复习笔记
本章作为《信号与系统》的开篇章节，是整个信号与系统学习的基础。

本章介绍了有关信号与系统的基本概念和术语，给出几种典型的信号和系统的表现形式，讲述了各信号与系统的特点以及信号之间的运算和转换。

通过本章学习，读者应掌握：如何判断信号类型、不同信号之间的运算、信号的分解以及系统类型的判断。

一、信号概述
1．信号的概念及分类（见表1-1-1）
表1-1-1信号的概念及分类
2．典型的连续信号（见表1-1-2）
表1-1-2典型的信号及表示形式
3．信号的运算（见表1-1-3）
表1-1-3信号的运算
4．阶跃函数和冲激函数
阶跃信号和冲激信号是信号与系统中最基础的两种信号，许多复杂信号皆可由二者或二者的线性组合表示。

具体见表1-1-4及表1-1-5。

（1）单位阶跃信号u（t）
表1-1-4单位阶跃信号u（t）
（2）单位冲激信号δ（t）
表1-1-5单位冲激信号δ（t）表示形式及性质
5．信号的分解
一个一般信号根据不同类型可分解为以下几种分量，具体见表1-1-6。

表1-1-6信号的分解
二、系统
1．系统概念及分类（见表1-1-7）
表1-1-7系统的概念及分类
系统模型如下：
输入信号经过不同系统可得到不同输出信号，具体见表1-1-8。

表1-1-8不同系统特性
1.2课后习题详解
1-1分别判断图1-2-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？
（a）
（b）
（c）
（d）
（e）
（f）。

《信号与系统》（第3版）习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。

1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。

[提示：f ( 2t )表示将f ( t )波形压缩，f (2t)表示将f ( t )波形展宽。

](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。

图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。

题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

S RS LS C题1-4图解 系统为反馈联接形式。

设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。

H i (s ) ；
(3)再取 H i ( s) 的逆变换得到此逆系统的冲激响应 hi (t ) ， 它应 当与第二章 2.9 节的结果一致。 解：(1)
r (t ) = e(t ) + ae(t − T ) ，对上式做 R( s) = 1 + ae −Ts E ( s)
1 1 + ae −Ts
L 变换得
欢 迎 访 问 慧 易 升 考 研 网 ：
0
下载更多清华大学信号与系统考研资料
所以 h ( t ) = ke* ( t0 − t ) = ke ( t0 − t ) = ke ( T − t ) ，
h ( t ) = ke (T − t ) = {cos[ωc (T − t )] + sin[ωc (T − t )]}[ u(T − t) − u(T − t − T )]
（2）由第二问的结论可知：
r (t ) = e(t ) * h(t ) = [cos(ωc t ) + sin(ωc t )][u (t ) − u (t − T )]*[cos(ωc t ) − sin(ωc t )][u (t ) − u(t − T )]
= t cos(ωc t )[u (t ) − u (t − T )] − (t − 2T ) cos(ωc t )[u (t − T ) − u (t − 2T )]
i →∞ i =0
认为线性时不变的，所以：
+∞
H [e(t )] = H [e(0 + )u (t ) + lim ∑ [e(ti +1 ) − e(ti )]u (t − ti )]
i →∞ i =0
+∞
= H [e(0+ )u (t )] + H [lim ∑ [ e(ti +1 ) − e(ti )]u( t − ti )]

第11章　反馈系统11.1　复习笔记反馈系统的研究是利用分解与互联概念而获得成功的典型范例。

本章的应用背景着重于控制工程，考察连续时间信号与系统的反馈系统模型并了解系统特性及应用，本章重点在于反馈系统框图及其系统特性。

通过本章学习，读者应掌握：反馈系统框图与系统函数的互求、根据系统函数画根轨迹图、开环特性稳定条件下的奈奎斯特判断依据以及信号流图与系统函数的互求。

一、反馈系统1．反馈效应的产生利用系统的输出去控制或调整系统自身的输入即可产生反馈效应。

（1）连续时间信号反馈系统模型如图11-1-1所示。

图11-1-1　连续时间信号反馈系统模型反馈系统的系统函数为：H（s）＝Y（s）/X（s）＝A（s）/[1＋F（s）A（s）]。

（2）离散时间信号反馈系统模型如图11-1-2所示。

反馈系统的系统函数为：H（z）＝Y（z）/X（z）＝A（z）/[1＋F（z）A（z）]。

图11-1-2　离散时间信号反馈系统模型【注】①若反馈信号与输入信号作相减运算，则称为负反馈或非再生反馈；②若反馈信号与输入信号作相加运算（即图11-1-1中加法器下面的符号改为正号），则称为正反馈或再生反馈。

2．反馈系统的特性及应用（见表11-1-1）表11-1-1　反馈系统的特性及应用3．利用反馈系统产生自激振荡（见表11-1-2）表11-1-2　反馈系统产生自激振荡二、根轨迹根轨迹是指闭环系统函数式中某种参量变动时，特征方程的根（极点）在s 平面内移动的轨迹（路径）。

1．根轨迹法的模量条件和幅角条件（1）模量条件1111||||||n n k k k k mm ii i i s pM K s z N ====-==-∏∏∏∏（2）幅角条件110π 0m ni k i k K r r K r ϕθ==>⎧-=⎨<⎩∑∑时为奇数时为偶数2．作图规则①根轨迹具有几条分支；②根轨迹始于开环系统函数A （s ）F （s ）的极点，止于A （s ）F （s ）的零点；③根轨迹对s 平面的实轴呈镜像对称；④若有一段实轴，在它右边的实轴上A （s ）F （s ）的极点与零点总数是奇数，则此段实轴是根轨迹的一部分；⑤两支根轨迹的交点可由方程d [()()]0d A s F s s=求出；⑥根轨迹为虚轴变点可由s ＝jω代入特征方程求出：1＋A （jω）F （jω）＝0；⑦当k→∞时，根轨迹各分支趋向A （s ）F （s ）的零点，其中有m 个分支趋于有限零点，另有（n －m ）个分支各自沿“渐近线”趋向无穷远处零点，渐近线与实轴交角为lπ/（n －m ），其中l ＝1，3，5···，共有（n －m ）个正奇数；⑧渐近线会交于实轴上的一点，此点称为渐近线重心，其坐标为：12120()()n m p p p z z z n mδ+++-+++=-L L 3．开环特性稳定条件下的奈奎斯特判断依据当ω由－∞到＋∞改变时，在A （jω）F （jω）平面中的奈奎斯特图顺时针绕（－1＋j0）点的次数等于系统函数分母G （s ）＝1＋F （s ）A （s ）在s 右半平面内的零点数（即系统函数H （s ）的极点数），此奈奎斯特图若不包围（－1＋j0）点，则系统稳定，否则系统不稳定。

《信号与系统》（第 3 版）习题解析高等教育出版社目录第 1 章习题解析 (2)第 2 章习题解析 (6)第 3 章习题解析 (16)第 4 章习题解析 (23)第 5 章习题解析 (31)第 6 章习题解析 (41)第 7 章习题解析 (49)第 8 章习题解析 (55)第 1 章习题解析1-1题 1-1 图示信号中， 哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c)(d)题 1-1图解 (a)、(c)、(d)为连续信号； (b)为离散信号； (d)为周期信号；其余为非周期信号； (a)、(b)、(c)为有始（因果）信号。

1-2 给定题 1-2 图示信号 f( t )，试画出下列信号的波形。

[提示： f( 2t )表示将 f( t )波形压缩，f( t)表示将 f( t )波形展宽。

]2(a) 2 f( t 2 )(b) f( 2t ) (c) f(t)2(d) f( t +1 )题1-2图解 以上各函数的波形如图 p1-2 所示。

图 p1-21-3如图1-3图示，R、L、C元件可以看成以电流为输入，电压为响应的简单线性系统S R、S L、 S C，试写出各系统响应电压与激励电流函数关系的表达式。

S RS LS C题 1-3图解各系统响应与输入的关系可分别表示为u R (t)R i R (t )u L (t)di L (t )L1dttu C (t )i C ( )dC1-4如题1-4图示系统由加法器、积分器和放大量为 a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。

题 1-4图解 系统为反馈联接形式。

设加法器的输出为 x( t )，由于x(t ) f (t) ( a) y(t)且y(t ) x(t)dt ,x(t) y (t)故有y (t) f (t ) ay (t)即y (t ) ay(t ) f (t)1-5已知某系统的输入 f( t )与输出 y( t )的关系为 y( t ) = | f( t )|，试判定该系统是否为线性时不变系统？解 设 T 为系统的运算子，则可以表示为y(t) T[ f (t )]f (t)不失一般性，设 f( t ) = f 1( t ) + f 2 ( t )，则T[ f 1 (t)]f 1 (t)y 1 (t )T[ f 2 (t)] f 2 (t )y 2 (t )故有T[ f (t)] f 1 (t )f 2 (t ) y(t)显然f 1 (t ) f 2 (t)f 1 (t ) f 2 (t )即不满足可加性，故为非线性时不变系统。

解：激励信号 e（t）＝e－3tu（t），则 E（jω）＝F[e（t）]＝F[e－3tu（t）]＝1/（jω＋3）
故响应为：
R( j) = E( j)×H ( j) = 1 ×1 = 1 - 1 j + 3 j + 2 j + 2 j + 3
反变换可得： r（t）＝F－1[R（jω）]＝（e－2t－e－3t）u（t）
1 / 50
圣才电子书

十万种考研考证电子书、题库视频学习平 台
图 5-1-1 线性网络的无失真传输 2．引起信号失真的原因 ①系统对信号中各频率分量幅度产生不同程度的衰减，使响应的各频率分量的相对幅 度发生变化，引起幅度失真； ②系统对各频率分量产生的相移与频率不成正比，使响应的各频率分量在时间轴上的 相对位置产生变化，引起相位失真。 三、滤波 1．理想低通滤波器（见表 5-1-1）
= jπ [e jtan- 11 ( + 1) - e- jtan- 11 ( - 1)] + jπ ×[e jtan- 13 ( + 3) - e- jtan- 13 ( - 3)]
2
10
反变换，可得：
r(t) = F - 1[R( j)]
= 1 sin(t - tan- 11) + 1 sin(3t - tan- 1 3)
5-2 若系统函数H（jω）＝1/（jω＋1），激励为周期信号e（t）＝sin（t） ＋sin（3t），试求响应r（t），画出e（t），r（t）波形，讨论经传输是否引起失真。
解：激励信号 e（t）＝sin（t）＋sin（3t），则 E（jω）＝F[e（t）]＝jπ[δ（ω＋1）－δ（ω－1）]＋jπ[δ（ω＋3）－δ（ω－3）]
6 / 50

，已知 y(-1)=0，y(-2)=0。 。
即
，解得
故全解为：
代入初始条件
，解得：
所以
y(n)
=
−
1 2
tan1 cos
nπ 2
+
1 2
sin
n
+
1 2
tan1
cos
n
u(n)
。
7-18 解差分方程
，已知 y(-1)=0
解得：
，故全解为：
代入初始条件 y(-1)=0，解得：
，
所以
。 。
7-15 解差分方程
，已知 y(0)=1。
解：由差分方程可得特征方程为 a+2=0，解得特征根 a=-2，故可设齐次解为
。
根据自由项形式设特解为
，将其代入原差分方程，则有
解得：
，故全解为：
。
代入初始条件 y(0)=1，解得：
，
所以
。
7-16 解差分方程
。 代入初始条件
，解得特征根 ，得
，解得
所以
。
（2）由特征方程
，解得特征根
。
代入初始条件
，得
，解得
所以
。
（3）由特征方程
，解得特征根
10 / 108
，故可设齐次解 ，故可设齐次解为： ，故可设齐次解为：

。 代入初始条件
所以
，得 ，解得
。
7-13 解差分方程
解：根据差分方程，可得特征方程为
4 / 108

所以 （3）当
时，有
，波形图如图 7-5（b）所示。
所以 所示。
，波形图如图 7-5（c）

!! ’! 已知双边 ! 变换为
& %" &#’ " # " # " # &## &#$ &#% # $ " &$# %’求原函数 (" "# !! " $ " # $ # &$$ #’求原函数 (" "# $
" # ! $ $ $$ &$$ %’求原函数 (" "# 解 ! 利用部分分式展开 ’将 %" &#表示为 # & & " & %" &#’ # ) # & ## & #$ & #% " #当 $ " &$# % 时 ’ "#是因果序列 ’故有 ("
#
" " # $ "#% ""
"
& ’ &$# $ $ & #$
" " )
所以 "" # " " ) " # $ ")" " $ # # # & " & &" " ( &#$ & ’ &* &$$ ’ !! !! % # # * ’ " # " # $ $$ " $ &#$ $ # &#" &#$ &# # !! !!
第 ! 章 ! 离散信号与系统的 " 域分析
习 题 七 详 解
!! #! 用定义求下列信号的双边 ! 变换及收敛域 ! " # # $!!!!!!!!!! " # " "" # $ " "# "## # "## !" #!" # " " " # $ " #" # $ $ # ##"# % "" "" #" #"#

信号与系统白皮书纠错表如果DSP复习得不错而且时间安排比较紧张, 那么白皮书的第7章可以不用太仔细地做. 第1章和第2章也只需略看一下. 其他各章的例题和习题推荐全做, 每年的考研题都有与白皮书上几乎一样的题型, 比如07年第一大题求Laplace变换的题目. 下面列出已发现的除第2,7,10章外的全部错误(包括习题题目错误,习题答案错误,例题解答错误等)及对应的修改方案. 我没有在下面列出来的题目都应该是正确的或只是图中有简单的标注遗漏;已经列出来的错误我都已经反复验算过, 但还是难免有错漏. 如果有问题可以与我联系, 我会及时更改. 相信这张表会对未来的413研友有所帮助. 注: 白皮书是指<<"信号与系统"解题指南>>, 科学出版社, 1999, 胡光锐,徐昌庆,谭政华,宫新保编.编号格式说明:a.b(c)表示白皮书第a章习题b第(c)小题;例a.b表示第a章例题b.白皮书错误表I(部分):说明: 第2,7,10章没做过不太清楚, 其他我认为还有问题的都列在下面,如有错误还请指正(例题单独注明,其他均为习题部分):3.1(b) 答案有错: 答案分子指数排版错误3.1(f) 书上没有给出答案,但不难求解4.24 答案有错: 答案少了2倍因子例 5.14 P190,式(5.14.6)分母计算错误:前三项的符号写反,导致后面的计算结果全错(但计算方法正确)5.18 题目有错: 电路图中互感M的两个箭头所指节点之间直接相连的导线应该删除,这样才能与答案相符5.23 题目似乎有错,没法做出结果.5.24 题目有错: 第一个全响应应该是因果信号,所以全响应后面应该加上阶跃函数u(t).答案也有错: +r(t)应改为+2r(t)5.27 答案有错: 系数1/5应该改为-1/26.12 答案有错: 第一问的答案应该是H(s)=1/(4s^2 + 2s + 1),后面的结果没有继续算下去6.16 题图有错: 前向增益的分母应改为(s+1)(s+3),这样计算的结果才能与答案一致6.20 答案有错: 分子中因式(1-H2)应改为(1+H2)7.4(c) 答案有错: 该信号显然是非周期信号. 如果把题目中的2次方指数放到sin函数之外,答案就对了7.7(f) 答案有错: 信号应该是非因果的8.1(e) 答案有错: 但如果将题目中的u[-n]改为u[n],就能和答案一致8.1(i) 答案有错: 但如果将题目中的a^|n|改为(a^n)u[n],就能和答案一致8.3 题目有错: 从答案看, 题目给出的频率π处的幅度值应该为π/2而非1/28.6 答案有错: 答案给出的是-x[n], 差了-1倍8.10 答案有错: 答案给出的Im{y[n]}正确, 但Re{y[n]}有错,因为他忘记了计算中频域还有一项时移因子,所以答案实际上只是Re{y[n-1]}9.1(d) 答案有错: 应该是3z - z/(z + 1/3), ROC: |z|<1/39.2(a) 答案有错: 答案分母正确分子有错,分子应该是z^4 -4z + 3, 整个分式还可以化简为(3 + 2z + z^2) / z^3, ROC:|z|>19.2(d) 答案有错: 答案的ROC不对, 应该是|z|>1/29.4(d) 答案有错: 答案里cos中的(nπ/4)应该改为(3nπ/4)9.6(2) 答案有错: 答案对应的Z变换是z(2z^2 - 1)/((z-1)(z-1/2)^2), 这却不是题目所给的Z变换9.8 答案中奇怪的系数0.17应该是1/6, 当然1/6≈0.179.9(b) 答案有错: 答案第一项1/6*n应该改为1/69.11(a) 答案有错: 少加了u[n]9.11(c) 答案有错: 答案里的u[n]应该加在所有表达式的最外层, 而且第一项也有错, -(-1/2)^(n-1)应该改为(-1/2)^(n+1)9.12 答案有错: 答案错得太离谱, 应该是h1[n]=[3/2 * (1/2)^n - 1/2 * (-1/2)^n] u[n]. 包图3楼吴大正的信号第3版习题 6.31与此题几乎完全相同,只是题目中的H3(z)=z/(z+1), 这时得到的答案为(1/2)^n * u[n], 有兴趣可以用这个再算算看自己的方法对不对白皮书错误表II(以下错误由frankwright于2006年10月22日发布, 修改信息是我后来添加的, 没有给出修改说明的题目是因为我找不到原来的解答了):3.1(d) 答案有错: 答案分母应该是π(1-4n^2)3.17(a)3.19(d) 答案有错: 答案中e的指数应该是-αt而不是-2t4.1(a)4.9(a)(b)5.5(c) 答案有错: 答案分母中的T^2应该改为T5.10(c) 答案有错: 答案第二个正弦项应该紧跟在sin后添加2倍系数5.28 答案有错: 答案的收敛域不完整, 应该为-1<Re[s]<28.1(b) 答案有错: 答案的分子1应改为4, 分母前的系数16应该删去8.4 这道题和答案我始终没看明白是什么意思, 有机会的同学不妨去问问老师8.5(c) 答案有错: 答案后两项中δ函数平移量4均应改为28.11(b) 题目有错: 题目表达式中1/2系数前的+号应该改为-号, 这样算出的答案才与白皮书一致8.13 答案有错: 答案应该为x[n] = {-3/8 * (-1/2)^n + n/4 * (1/2)^n + 3/8 *(1/2)^n} u[n-1]8.14(b) 答案有错: 答案应该为4/5 * (-1)^n9.6(1(b))答案有错:答案第一项中的ε(-n)应改为ε(-n-1)终于打完了. 祝未来考研的朋友们好运!。