现代控制理论刘豹第三版印刷勘误表

精心整理绪论为了帮助大家在期末复习中能更全面地掌握书中知识点，并且在以后参加考研考博考试直到工作中，为大家提供一个理论参考依据，我们11级自动化二班的同学们在王整风教授的带领下合力编写了这本《现代控制理论习题集》（刘豹第三版），希望大家好好利用这本辅助工具。

根据老师要求，本次任务分组化，责任到个人。

我们班整体分为五大组，每组负责整理一章习题，每个人的任务由组长具体分配，一个人大概分1~2道题，每个人任务虽然不算多，但也给同学们提出了要求：1.写清题号，抄题，画图（用CAD或word画）。

2.题解详略得当，老师要求的步骤必须写上。

3.遇到一题多解，要尽量写出多种方法。

本习题集贯穿全书，为大家展示了控制理论的基础、性质和控制一个动态系统的四个基本步骤，即建模、系统辨识、信号处理、综合控制输入。

我们紧贴原课本，强调运用统一、联系的方法分析处理每一道题，将各章节的知识点都有机地整合在一起，力争做到了对控制理论概念阐述明确，给每道题的解析赋予了较强的物理概念及工程背景。

在课后题中出现的本章节重难点部分，我们加上了必要的文字和图例说明，让读者感觉每一题都思路清晰，简单明了，由于我们给习题配以多种解法，更有助于发散大家的思维，做到举一反三！这本书是由11级自动化二班《现代控制理论》授课老师王整风教授全程监管，魏琳琳同学负责分组和发布任务书，由五个小组组组长李卓钰、程俊辉、林玉松、王亚楠、张宝峰负责自己章节的初步审核，然后汇总到胡玉皓同学那里，并由他做最后的总审核工作，绪论是段培龙同学和付博同学共同编写的。

本书耗时两周，在同学的共同努力下完成，是二班大家庭里又一份智慧和努力的结晶，望大家能够合理使用，如发现错误请及时通知，欢迎大家的批评指正！2014年6月2日第一章 控制系统的状态空间表达式1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式 解：系统的模拟结构图如下： 系统的状态方程如下： 令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为1-2有电路如图1-28所示。

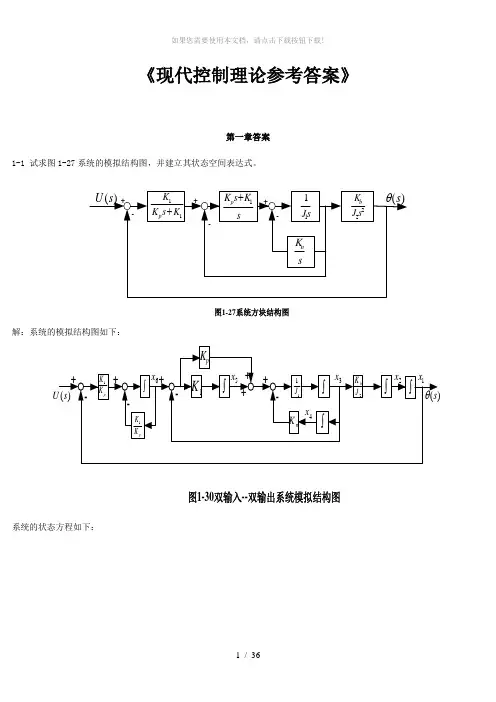
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：uK K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x p p pp n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

L1L2U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

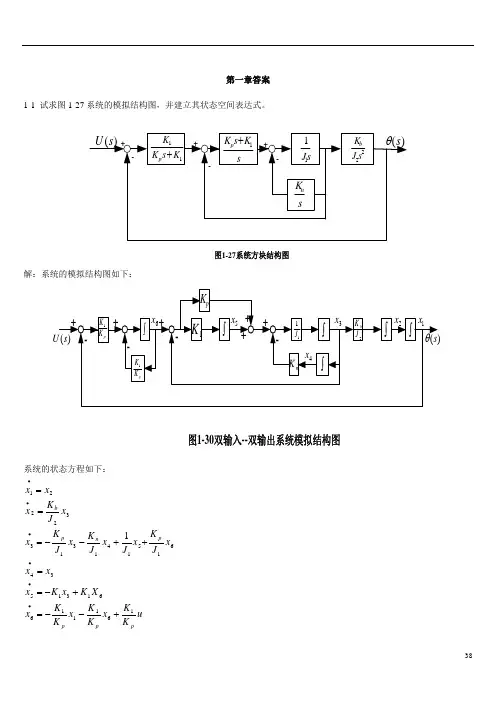
第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

bpppp K x x x x J xx K xJx K K K x x u K K K xJ J K x x p x K xK xxx Ax+Buy=CxA=BCM Mf f M MM y f K c c B y yM y f K c B y K c c B y yffx Ax+Buy=CxA=By y y y u usG ss s sa a ab b bAB n n n b nba a ab a b aC bba b a a b a aabb a b a T TBCa ab a aa aa aaby y y y u u us sG ss s sb b b bCBTW s C SI A B d SI ASSS S S S SSSSSAA P P P A P P P T P P TPPP P T ATJ T ATT BCTW s W s I W s W s2 4.At e10140 A5 15!4!Atett 11A P P112T jP222A P P212T jP1122Tj j412cos 2sin 214sin 22cos 22At t tt e Te T t t 112111()444S S SI A S SS22t t 22))jt jt e21141A223323232233112!3!13715,2!66281344,1562!At e I AtA t A t t t t t t t t t t t t t 6e At e 3031()31()4t tt t t e e t e e 0Ate I 1T2.010001(1,0)xx u y x 1(0),()1x u t 22.1...2!A I Att ()00201()122111222tAt A t t t td t td t x x = =01te e Bu d)(10t t 110110110t27.231.00()()(0)(),()At At t t x x x t e x e t u K BK Ku ()00()t At A t e e B d x x K ()00()t At A t e e d x B ()00|At A t e e0At At e e B x 2t t u K 0(0)x x ()01()t d ()00t At A t e e d B x K 1()00|At A t t e A e B x K 10()At At e A e I B x K 1x x K Kx K B K ()1()A e e B t 0At t3()1()t t u k 0(0)x x ()00(t)1()tAt A t e eB t d x x K 00tAt A At e e d e B x K ()'A A e e A e A 0t 000|t t A tA A e e d A e A 0|t110|A A t Ate A e 11()A At A te A e I 210()()At At At At t e A e I A tee B x x 210()At At e A e I A t B x KK d 00t 1t A A e d Ae e d2-9.2-21s,0.1T s 11u 2u 111212x x Ku x x u 12u u y210120;1.11110010I A P P 1101T P 22200011I A P P 112P 0111T 1T 11101100()0AT T T G T eT T e e 000()0101001(1)T TAt t T T K H T e dtBdt e e K e K T e T T 111Te t e 11K T e TT 0(1)011221212(1)()()()()(1)()()()0()11()(1)0()(1)T TT T12x k x k G T H T u k x k x k x k ex k eu k K e u k K T e T12()()21()u k x k y k x k 0.1Ts0.110.1210.12(1)0(1)()()x k ex k e K e u k K e12()()21()x k y k x k 1Ts10.1)(1x k ()x k ()u k 12109).9)0.9)0.1(1111221112(1)()0(1)()11()(1)0()1x k x k e x k x k eu k K e u k Ke12()()21()x k y k x k 112222(1)()()()(1)()()()()100()()10x k x k u k TA I TBx k x k u k x k u k T KT x k u k TT20.1T ss12112212(1)()0.90(1)()0.11()0.10()0.1x k x k x k x k u k K u k 1T 1122(1)()()000(1)()()111x k x k u k K x k x k u k 1111At e t2AB BA3-11x u2x4 ya, b, c, d1122334412340001000110000100010x x a x x b u x x c x x dx x yx x 02M b AbA bA b 22100001001a a a a c a ac c a c d,a, b, c, d4rankM 323223222230011100C CA c NCA a c b c cCA a ac c b bc c c 4rankN 00,a, b, c, d 222121110x x a b u x x c dx yx 11b a M b Abc d11b a Ma b c c dda b c d1110C NCA a bb3abcdabcd331121[]1M b Ab 210M211211C NCA 21N212121234A 11b10c 123411M bAbrank 2M 3412det 0M12341TC N C CACA2det 0N20432233231341322232831441333232223232332232323det 1410142510486624M M 012123b Ab A b1220010141413C NCA CA det 0N 32226825()14343s s s W s s s s s I 0134A 01b52Tc1II01TA2b 01T 1d 311200011012MbA bdet 0M 3rankM 3425d c Ab010001100cR det 0c3R 1cR 0011000101014ˆ1202c cA R AR 1ˆ100Tc b R b cc cR 3()W s 231()1s s W s s s2111231001001001001sss12101,,10010000r r rrrI A I II200100100r crrI0010000000000011010000000000000000002r00000000,001001r cr rB I 012cC 00:20000000000c cc cC NC A C A 100011001000001000()36Rank N c 1010100100000110011o R 1000110011000000001000010100000010000o R 00000100110010000010001000oR 100000010121212121ˆˆˆˆ0000000000000000ˆ00110000100011001000o oA AR AR AAA 1ˆˆ1000ˆ00o BBB R B10000112ˆ0ˆˆoCCR C C 100100000001211111111ˆˆˆ00110ˆˆ100,00,00001100ˆ010m mA B C W AA B B C C W s 23()11001001001001ss W s s s s s s120012000110,,011000312()01200000000000000100000001000000010000100mm m om m mmmmIA I I I I 000,0100B 00001000000001o m m mC I :1000101122000000010000010000100100100100001001o o o ooMB A B A B 36rankM 1cR 010010100000100100001000cR 0010000100001000100010000000001000110011000100000cR 10110ˆc o cAR A R 000010100000010100ˆ00000c oBR B 00000000000000000001100100ˆ001000o cCC R 11111111ˆˆˆ010ˆˆ000,100100ˆ001m mA B C W AA B B C C 1n 1001,00M b Ab A b1nA 233-33234-11()TQ P x x 121322233233P P P P P P P P P x 110112131P =0220317.750i221101003()Q x 2TQ x x 131P11233160()Q x ()117.75ix P 11434-22112211221221A a a a a a a1211221211221221a aa a a aQ IPTA12221222122221221001 a a P P P P a a11112112()1a P a P211211221112122()a a P a P a P121221222()1a P a PP=11P1221222P PAP PA QP Pa a P P a a1121111211121112112r P t A A222r P t A A11222111122r a a a a P t A A r t AA1122r t A a a 11221221A a a a a P11P 112212244r r P P P t A At A A22111212212()()04r a a a a t A A 112212210A a a a a 11P 0A0r t A 1122a a 112212210a a a a 1122a a 4-3121()v x22x x 0ex ()0v x22121()266v x x x x x 2336PP 2i0iiiP ()0v x x()v x TA P PAQQI302x xP T111P120P22212()v xx x11x 22x5-21120010,,01011010100990Mb Ab A b 3rankM)100k 2010,,01011010100990M b Ab A b 3rankM2I321111A1112112212100100010010110100111019901001011111 cIT A b Ab b10cIA20120100011111A bKb T0.13221()(11)(11)f *32()122440f 40131K314 1.20.c KKT 15-512Mb Ab A b 24001015det 0M 5-8(1);1100200c A B20121010det detdet10c A B c A B Ec A B;RankM 13kMc A B 05-10(1)cNcA(2)II:01y cTx x(3)12,gGg :12221()det()1g f I A Gc g g g (4):*2()()(2)322f r r rr(*222113ˆ;2002rrx u y rr2ˆˆˆ()0113ˆˆ()002Ax bu G y y r;x u y yr(1)(2)22101- =10000g g A Gc g g 2121=detf I A Gcg g g :*2()()(2)322f r r r r232r Gr12g 11)(det[(-)]。

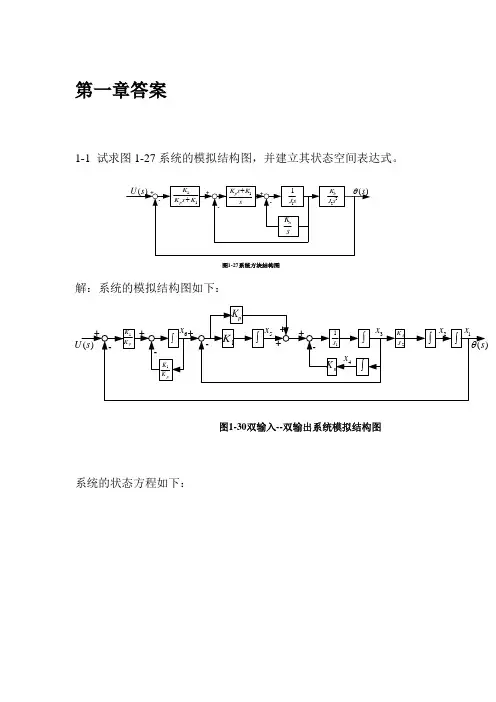
第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿 令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙6543211654321111111126543210000010000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

R1L1R2L2CU---------Uc ---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。

1、 第29页 式1.34中最后一个1n β- 改为1β。

2、 36页 分为：“（1）A 阵的特征值无重根；（2）A 阵的特征值有重根；”这样的分法不是很严密，建议应该为：“（1）A 有n 个线性无关的特征向量；（2）线性无关的特征向量数少于n ” 3、 48页上面W(s)中的第三行=号左面的“111()SI A B --”应移到上一行最末尾。

避免误解。

4、 67页2.24式应改为：111221111(1)!011(2)!2(1)(2)312!2!12111!1!2111121()0001()000(1)()001()012()1n n t t n t t n n n n t t n t n t n n t n e t t n e t e t e t e λλλλλααλαλαλλαλλλ-------------⎡⎡⎤⎡⎤⎢⎢⎥⎢⎥-⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢=⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎤⎥⎥⎥⎥⎥⎥⎥⎢⎥⎦5、 70页2.32式最后 1tA-改为1A t -6、 97页第一行12111001012T λλλ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦7、 100页 例3-8 2244120100142100A B ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦应该改为22440101001100042A B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ 或者改为 2121010103120110A B ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦8、 103页图3.7中 12,y y 的输出箭头不应该指向211,m c c ，应断开。

9、 126页 例3-12中224()168121216M b AbA b ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦10、 130页用对偶原理证明，有待考证。

表述不明确。

另外最后倒数第二行能控标准I行，应该改为能观标准I 型。

11、 144页式（3.124）0lim ()s D W s →= 改为lim ()s D W s →∞=12、 145页式（3.133）下一行，“m 为输入矢量维数。

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。

图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：uK K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x p p pp n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。

以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。

L1L2U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。