高二物理 简谐运动及其描述
- 格式:doc
- 大小:68.50 KB
- 文档页数:4








高中物理知识点总结-简谐运动
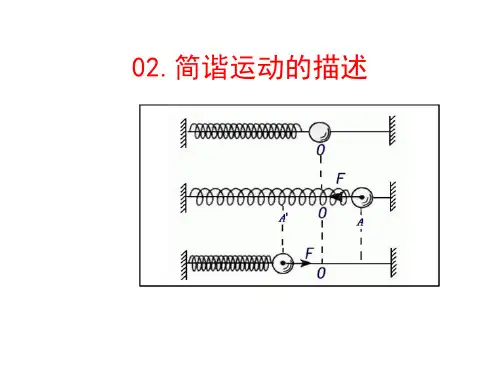
简谐运动(1)定义:物体在跟偏离平衡位置的位移大小成正比,并且总是指向平衡位置的回复力的作用下的振动,叫做简谐运动.(2)简谐运动的特征:回复力F=-kx,加速度a=-kx/m,方向与位移方向相反,总指向平衡位置.简谐运动是一种变加速运动,在平衡位置时,速度最大,加速度为零;在最大位移处,速度为零,加速度最大.(3)描述简谐运动的物理量①位移x:由平衡位置指向振动质点所在位置的有向线段,是矢量,其最大值等于振幅.②振幅A:振动物体离开平衡位置的最大距离,是标量,表示振动的强弱.③周期T和频率f:表示振动快慢的物理量,二者互为倒数关系,即T=1/f.(4)简谐运动的图像①意义:表示振动物体位移随时间变化的规律,注意振动图像不是质点的运动轨迹.②特点:简谐运动的图像是正弦(或余弦)曲线.③应用:可直观地读取振幅A、周期T以及各时刻的位移x,判定回复力、加速度方向,判定某段时间内位移、回复力、加速度、速度、动能、势能的变化情况.。
简谐运动的描述知识集结知识元简谐运动的振幅、周期和频率知识讲解2.相关物理量:①振幅A:振动物体离开平衡位置的最大距离。
②周期T:做简谐运动的物体完成一次全振动所需要的时间。
③频率f:单位时间内完成全振动的次数。
④相位:描述周期性运动在各个时刻所处的不同状态。
3.受力特征:①做简谐运动的质点受到的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,通常将这种力称为回复力。
②回复力:F=-kx③若质点受到的回复力为F=-kx,则质点的运动为简谐运动。
4.运动特征位移x:方向始终背离平衡位置,每经过平衡位置位移方向发生改变;远离平衡位置时位移增大,靠近平衡位置时位移减小。
速度v:每经过最大距离处速度方向发生改变,远离平衡位置时速度方向和位移方向相同,靠近平衡位置时速度方向和位移方向相反。
加速度,方向与位移方向相反,总指向平衡位置.简谐运动是一种变加速运动.在平衡位置时,速度最大,加速度为零;在最大位移处,速度为零,加速度最大。
5.振动能量简谐运动过程中动能和势能相互转化,机械能守恒.振动能量与振幅有关,振幅越大,能量越大。
6.周期性:简谐运动是一种复杂的非匀变速运动,要结合牛顿运动定律、动量定理、动能定理、机械能守恒定律来分析解决简谐运动的问题。
(1)简谐运动的对称性:振动物体在振动的过程中,在关于平衡位置对称的位置上,描述物体振动状态的物理量(位移、速度、加速度、动量、动能、势能等)大小相等。
(2)简谐运动的周期性:振动物体完成一次全振动(或振动经过一个周期),描述物体振动状态的物理量(位移、速度、加速度、动量、动能、势能等)又恢复到和原来一样。
简谐运动的周期是由振动系统的特性决定的,与振幅无关。
弹簧振子的周期只决定于弹簧的劲度系数和振子的质量,与其放置的环境和方式无关。
例题精讲简谐运动的振幅、周期和频率例1.如图所示,一质点在x轴上以O为平衡位置做简谐运动,其振幅为8cm,周期为4s。
t=0时物体在x=4cm处,向x轴负方向运动,则()A.质点在t=1.0s时所处的位置为x=+4cmB.质点在t=1.0s时所处的位置为x=-4cmC.由起始位置运动到x=-4cm处所需的最短时间为sD.由起始位罝运动到x=-4cm处所需的最短时间为s例2.如图所示,一质点在平衡位置O点附近做简谐运动,若从质点通过O点时开始计时,经过0.9s质点第一次通过M点,再继续运动,又经过0.6s质点第二次通过M点,该质点第三次通过M点需再经过的时间可能是()A.1s B.1.2s C.2.4s D.4.2s例3.如图1所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动。

简谐运动1. 引言简谐运动是物理学中非常重要的一个概念,它描述的是一个系统围绕平衡位置做周期性运动的特性。
简谐运动在力学、波动和振动等领域中有广泛的应用,并且在现实世界中存在着很多例子。
本文将对简谐运动的定义、特点以及相关公式进行总结和分析。
2. 简谐运动的定义在物理学中,简谐运动指的是一个物体围绕平衡位置做周期性运动的特性。
当物体受到一个恢复力(如弹簧的弹性力)与位移成正比时,就会发生简谐运动。
简谐运动是一个理想化的模型,它假设系统没有阻尼和外界干扰。
3. 简谐运动的特点(1)周期性:简谐运动是一个周期性运动,物体在一定时间内完成一个完整的往复过程,即回到起始位置。
(2)恢复力与位移成正比:简谐运动的恢复力与物体的位移成正比,当物体偏离平衡位置越远时,恢复力越大。
(3)最大速度和最大加速度发生在平衡位置:在简谐运动中,物体的最大速度和最大加速度发生在物体通过平衡位置时。
(4)能量守恒:在完全没有阻尼和外界干扰的情况下,简谐振动系统的总能量保持不变,由势能和动能的转化而来。
4. 简谐运动的描述简谐运动可以用以下几个重要的物理量来描述:(1)位移(y):物体相对于平衡位置的偏移量。
(2)周期(T):完成一个完整的往复运动所需要的时间。
(3)频率(f):单位时间内完成的往复运动的次数,与周期的倒数成正比(f =1/T)。
(4)角频率(ω):即角速度,表示在单位时间内的相位增加的量,与频率成正比(ω = 2πf)。
(5)振幅(A):简谐运动的最大位移,即离开平衡位置的最大距离。
5. 简谐运动的公式简谐运动的位移(y)、速度(v)和加速度(a)可以用以下公式来表示:(1)位移:y = A * sin(ωt + φ) (2)速度:v = A * ω * cos(ωt + φ) (3)加速度:a = -A* ω^2 * sin(ωt + φ)其中,A表示振幅,ω表示角频率,t表示时间,φ表示初相位。
6. 简谐运动的力学模型对于一个质点来说,受到简谐力的作用时,可以将其运动描述为一个简谐振动系统。
高二物理第九章简谐运动知识点归纳
(1)简谐运动:
物体在跟位移大小成正比,且总是指向平衡位置的力作用下的振动。
受力特征:kxf对简谐运动的理解:
①简谐振动是最简单最基本的振动
②简谐运动的位移按正弦规律变化,所以它不是匀变速运动,而是变力作用下的非匀变速运动。
③简谐运动具有重复*的运动轨迹,若轨迹不重复,则一定不是简谐运动。
(2)描述简谐运动的物理量
平衡位置:做往复运动的物体能够静止的位置,叫作平衡位置。
振动:物体(或其一部分)在平衡位置附近所做的往复运动,对振动的三点透析:
振动的轨迹:振动物体可能作直线运动,也可能做曲线运动,所以其轨迹可能是直线或曲线。
振动的特征:往复*。
振动的条件:每当物体离开平衡位置后,它就受到一个指向平衡位置的力,该力使物体产生回到平衡位置的效果(即回复力)、并将其看作受到的阻力足够小。
此时认为它做自由振动。
振幅a:
定义:振动物体离开平衡位置的最大距离,叫作振动的振幅(或省略作振幅)单位:m(米)
物理意义:反映振动的强弱和振动的空间范围,对同一系统,振幅越大,系统的能量越大。
振幅和位移的区别
1.振幅是振动物体离开平衡位置的最大距离,位移是振动物体相对平衡位置的位置变化
2.振幅时表示振动强弱的物理量,位移表示的是某一时刻振动质点的位置。
3.振幅是标量,位移是矢量周期t:
定义:做简谐运动的物体完成一次全振动所需要的时间。
单位:s 物理意义:表示振动的快慢,周期越长表示物体振动的越慢,周期越短表示物体振动得越快。
引言概述:简谐运动是物理学中的一个重要概念,它在生活中随处可见。
本文将对简谐运动的知识进行总结,以帮助读者全面理解和掌握简谐运动的相关概念和特性。
正文内容:一、简谐运动的定义与描述1.简谐运动的定义:简谐运动是指物体在一个恢复力作用下沿直线或者围绕固定轴线进行的运动,其加速度与位移成正比且反向相同。
2.简谐运动的描述:简谐运动可以用位移、速度、加速度等物理量对其进行描述,其中位移随时间的变化呈正弦函数。
二、简谐运动的特性1.周期性:简谐运动具有周期性,即物体在一次完整运动中所经历的时间是一定的。
2.频率:简谐运动的频率是指单位时间内完成的运动周期数,其与周期有倒数关系。
3.振幅:简谐运动的振幅是指物体在运动过程中离开平衡位置的最大位移。
4.相位:简谐运动的相位是指物体在简谐运动中的位置关系,可以通过相位角来描述。
5.能量守恒:简谐运动中,机械能守恒,包括动能和势能的转化。
三、简谐振动的数学表达1.位移方程:简谐运动可以通过位移方程进行数学表达,一般形式为x(t)=Asin(ωt+φ),其中A为振幅,ω为角频率,φ为初相位。
2.速度和加速度方程:简谐运动的速度和加速度可以通过对位移方程分别进行一次和两次时间导数得到。
四、简谐振动的应用1.机械振动:简谐振动在机械工程中有广泛应用,如弹簧振子、钟摆等。
2.电磁振动:简谐振动在电磁学中的应用包括交流电路中的振荡器、天线振动等。
3.光学振动:简谐振动在光学中的应用包括光的偏振、干涉等现象。
4.生物振动:简谐振动在生物学中有许多应用,如心脏的收缩与舒张、呼吸等。
5.音乐演奏:音乐演奏中的乐器振动可以用简谐振动进行描述,如弦乐器、风笛等。
五、简谐振动的干扰和共振1.干扰:两个简谐振动相互作用可以产生干扰,如合成振动和干涉现象。
2.共振:当外界周期性力与物体的固有振动频率相同或接近时,会发生共振现象,产生巨大振幅。
总结:通过对简谐运动的定义与描述、特性、数学表达、应用以及干扰和共振的介绍,我们可以更全面地理解和掌握简谐运动的相关知识。
高二物理简谐运动及其描述
教学目标
1.知道简谐运动的概念,掌握简谐运动图像的获取方法;
2.理解简谐运动的图像特点及表达式,会根据图像分析简谐运动;
3.知道相位、初相位、周期、频率、振幅、位移等一系列描述简谐运动的基本概念。
4.了解生活中的简谐运动
5.掌握对简谐运动的研究方法:实验法,数学图像法和函数法
教学重点
简谐运动的图像获取及分析
用函数及图像表达简谐运动
理解简谐运动的系列概念的物理意义
教学难点
简谐运动的表达式
教学课时
两课时
教学资源
水摆、课件
教学方法
实验探究,自学讨论,归纳总结,推广应用
教学过程
第一课时简谐运动的基本知识
引入:播放一段二胡曲«良宵»――――优美的声音来自琴弦的振动
学生列举生活中的振动――上课铃声,耳膜的振动,高层建筑随风摆动,机器的有节奏的
轰鸣,扁担的晃动,某些同学上课时腿的抖动。
新课:
一.机械振动
1.概念:物体在某一位置附近来回往复的运动即为机械振动,简称振动。
2.平衡位置
简介―――弹簧振子(结构,运动演示)
振动图像的获取方法:
A―――水摆法(实验:在行间匀速走动,地上留下水摆的图像)
B----- 频闪照相描迹法(观看课件:描迹法作图像)
二.简谐运动
1.概念:质点的位移时间关系遵从正弦函数规律的振动叫做简谐振动
2.图像的绘制:课本P4 例子三个
思考与讨论:课本P5 ex2 拉动纸带法记录
三.描述简谐运动的物理量
1. 振幅:振动物体离开平衡位置的最大距离
2. 周期:一次全振动的时间T
频率:单位时间内全振动的次数f=1/T
说出以下频率的数量级:交流电,可见光,腿的抖动
自学课本P10 科学漫步乐音和音阶
3.相位:周期性运动在不同时刻所处的状态
如:右侧的两个单摆在同步摆动和异步摆动时的相位关系(超前与滞后)科学漫步―――月相
课堂作业:
教后记:
第二课时简谐运动的表达式
复习及引入:
1.一块熏满黑烟的玻璃板沿竖直方向匀速下移,同时有一尖针
在水平方向作简谐运动并在玻璃板上留下划痕,试判断
此划痕的形状及反映的物理信息。
如果玻璃板做自由落体运动呢?
2.一质点从图示的A位置开始以角速度ω=2πrad/s做半径为R=10cm的匀速圆周运动,其在y方向上做何种运动?(振动!)是否简谐运动?
Y方向:
X方向:
新课;
一简谐运动的表达式及图像
1.表达式X=Asin(ωt+φ)
ω=2π /T=2πf
2.物理意义:反映了物体相对平衡位置的位移随时间变化的关系
3.图像:位移-时间图像
作出引例2中振动图像如下:
写出振动方程.
二.图像分析
1.速度,位移分析(两种位移的不同含义)
2.周期性分析
例题1.以下说法正确的是:c
A、若t时刻和(t+Δt)时刻振子运动的位移大小相等,方向相同,则Δt一定等于T的
整数倍。
B. 若t时刻和(t+Δt)时刻振子运动的运动速度大小相等,方向相反,则Δt一定等于
T/2的整数倍。
C、若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相同。
D、若Δt=T/2,则在t时刻和(t+Δt)时刻弹簧的长度一定相等。
例题2:一个质点在平衡位置O点附近做简谐运动,若从O点开始计时,经过3s质点第一次经过M点;若再继续运动,又经过2s它第二次经过M点;则质点第三次经过M点所需要的时间是:③④
①8s ②4s ③14s ④(10/3)s
课堂作业:
教后记:。