小学三年级数学下册《面积》重要知识点

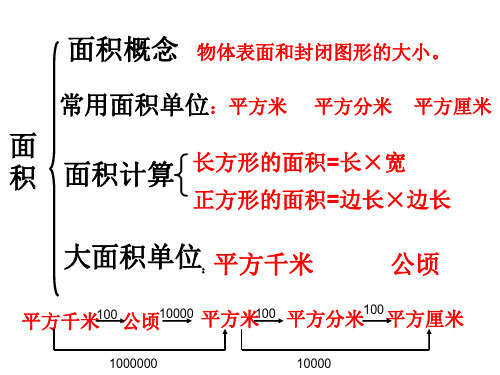
【篇一】小學三年級下冊數學《面積》知識點1、物體的表面或封閉圖形的大小，就是他們的面積。

2、比較兩個圖形面積的大小，要用統一的面積單位來測量。

3、常用的面積單位有平方釐米（cm2），平方分米（dm2）、平方米（m2）。

4、邊長1釐米的正方形面積是1平方釐米。

5、邊長1分米的正方形面積是1平方分米。

6、邊長1米的正方形面積是1平方米。

7、邊長100米的正方形面積是1公頃（10000平方米）。

8、邊長1千米（1000米）的正方形面積是1平方千米。

9、測量土地的面積時，常常要用到更大的面積單位：公頃、平方千米。

平方千米公頃平方米平方分米平方釐米10、長方形的面積=長×寬長=面積÷寬寬=面積÷長11、正方形的面積=邊長×邊長12、長方形的周長=（長+寬）×2寬=周長÷2-長長=周長÷2-寬13、正方形的周長=邊長×414、正方形的邊長=周長÷415、相鄰的兩個常用的長度單位間的進率是10。

16、相鄰的兩個常用的面積單位間的進率是100。

17、1平方米=100平方分米；1平方分米=100平方釐米；1公頃=10000平方米；1平方千米=100公頃（公頃、平方千米這兩個土地面積單位間的進率是100。

）注：面積和周長是不能相比較的；分清楚什麼時候填長度單位，什麼時候填面積單位，填土地面積單位時，比較小的土地面積（如：公園、體育場館、超市、果園、廣場）等一般情況下填公頃；（城市的占地、國家的面積、江河湖海的面積）等一般情況下填平方千米。

面積相等的兩個圖形，周長不一定相等。

注意：周長相等的兩個圖形，面積不一定相等。

【篇二】小學三年級下冊數學《面積》教案教學目標：1、通過比一比使學生初步感知面積的含義。

2、讓學生經歷比較幾個圖形面積大小的過程，體驗比較策略的多樣性。

3、通過學生參與畫圖活動，進一步認識圖形面積的含義。

4、在活動中培養學生的動手操作能力、分析綜合能力和初步的空間觀念，並培養學生與人合作交流的能力。

第五单元《面积》知识点归纳总结（一）面积的定义1、面积物体表面或封闭图形的大小，叫做它们的面积。

1平方米：边长是1米的正方形，它的面积是1平方米。

1平方分米：边长是1分米的正方形，它的面积是1平方分米。

1平方厘米：边长是1厘米的正方形，它的面积是1平方厘米。

2、生活中的1平方厘米、1平方分米、1平方米1平方厘米（指甲盖）、1平方分米（电脑光盘或电线插座）、1平方米（教室侧面的小展板）。

注意：①面积指的是封闭图形的大小，不是封闭图形没有具体面积。

②长度单位和面积单位之间不能比较大小。

（二）面积单位间的进率①进率100：1平方米= 100平方分米1平方分米= 100平方厘米②进率10000：1平方米= 10000平方厘米③进率1000000：1平方千米= 1000000平方米④相邻两个常用的长度单位之间的进率是10 ；相邻两个常用的面积单位之间的进率是100 。

（三）面积单位间的转化一看：看是高级单位转化成低级单位，还是低级单位转化成高级单位；二想：想进率是多少；三转：①高级单位→低级单位，×进率②低级单位→高级单位，÷进率（四）周长公式长方形的周长= （长＋宽）×2长= 周长÷2－宽或者：（周长－长×2）÷2= 宽宽= 周长÷2－长或者：（周长-宽×2）÷2=长正方形的周长= 边长×4正方形的边长= 周长÷4（五）面积公式长方形的面积=长×宽正方形的面积=边长×边长长方形的周长=（长+宽）×2正方形的周长=边长×4已知面积求长：长=面积÷宽已知面积求边长：边长=面积开平方已知周长求长：长=周长÷2 - 宽已知面积求边长：边长=面积÷4（六）铺砖问题1、地面面积÷地砖面积=总块数2、沿长铺的块数(地面长÷地砖边长) ×沿宽铺的块数(地面宽÷地砖边长) =总块数（七）常见题型1、求周长：缝花边、围栅栏、围栏杆、池塘或花坛周围小路长度、围操场跑步的长度······2、求面积：课本等封面大小、刷墙、花坛面积、给餐桌配玻璃、洒水车洒到的地面······3、粉刷刷墙（有的中间有黑板、窗户等）：用大面积－小面积。

常用的面积单位问题导入你知道哪些面积单位？认一认。

过程讲解1．明确常用的面积单位常用的面积单位有平方厘米、平方分米和平方米。

2．意义讲解(1)认识平方厘米。

①规定：边长为1厘米的正方形的面积是1平方厘米，如图：1平方厘米可以表示为1cm2，读作1平方厘米。

②实例展示：一粒纽扣表面的面积大约是1cm2，一粒蚕豆表面的面积大约是1cm2…③测量数学书封面的面积：用面积是1cm2的小方格测量数学书封面的面积，结果大约是468cm2。

(2)认识平方分米。

如果用面积是1cm2的小方格来测量课桌桌面的面积，要用很长时间才能测量完。

1cm2用来测量较小的物体的面积较合适，对于稍大的物体可以选择稍大的面积单位，即选边长为1分米的正方形的面积为单位。

①规定：边长为1分米的正方形的面积是1平方分米。

1平方分米可以表示为1dm2，读作1平方分米。

②实例展示：成年人手掌表面的面积大约是1dm2……③测量课桌桌面的面积：用面积是1dm2的正方形量一量，课桌桌面的面积大约是24dm2。

(3)认识平方米。

黑板表面的面积比课桌桌面的面积要大得多，测量它的面积，应该用比平方分米大的面积单位——平方米。

①规定：边长为1米的正方形的面积是1平方米。

1平方米可以表示为1m2，读作1平方米。

②实例展示：一般家里吃饭用的餐桌桌面的面积大约是1m2，4个小朋友手拉手站成一个正方形，所围成的面积大约是1m2……③测量黑板面的面积：用面积是1m2的正方形测量黑板面的面积，黑板面的面积大约是4m2。

归纳总结1．常用的面积单位有平方厘米、平方分米和平方米，可以分别用字母cm2、dm2和m2来表示。

2．平方厘米用来测量较小物体表面或图形的面积；平方分米用来测量稍大物体表面或图形的面积；平方米用来测量较大物体表面或图形的面积。

3．常用的三个面积单位相比较，1平方厘米＜1平方分米＜1平方米。

一、面积的意义物体的表面或封闭图形的大小，就是他们的面积。

二、长度单位与面积单位的区别用长度单位表示物体的长短或封闭图形一周的长度；用面积单位表示物体表面或封闭图形的大小。

注：面积和周长是不能相比较的；分清楚什么时候填长度单位，什么时候填面积单位。

三、比较两个图形面积的大小要用统一的面积单位来测量和比较。

四、常用的面积单位有平方厘米（cm2）；平方分米（dm2）；平方米（m2）。

1、边长1厘米的正方形面积是1平方厘米。

反过来，面积是1平方厘米的正方形，它的边长是1厘米2、边长1分米的正方形面积是1平方分米。

反过来，面积是1平方分米的正方形，它的边长是1分米3、边长1米的正方形面积是1平方米。

反过来，面积是1平方米的正方形，它的边长是1米五、面积单位间的换算大单位化成小单位，用大单位前面的数乘进率；小单位化成大单位，用小单位前面的数除以进率。

1平方米=100平方分米；1平方分米=100平方厘米六、面积和周长公式长方形的面积=长×宽长=面积÷宽 宽=面积 ÷长正方形的面积=边长×边长长方形的周长=(长+宽)×2宽 = 周长÷2-长 长=周长÷2-宽正方形的周长=边长×4正方形的边长=周长÷4注意：面积相等的两个图形，它们周长不一定相等。

周长相等的两个图形面积不一定相等。

面积相等的长方形、正方形中，长方形的周长最长；周长相等的长方形、正方形中，正方形面积最大.七、铺地砖问题①先算出所铺地面的总面积；②计算出每块地砖的面积；③将这两个面积统一成相同的面积单位；④地砖的总块数=所铺地面的总面积÷每块地砖的面积.一、填空1、长方形的面积＝( )×( )正方形的面积＝( )×( )正方形的周长＝( )×( )2、长方形的长16厘米，宽12厘米，它的周长是( )厘米，面积是( )平方厘米。

三年级数学面积常用知识点总结面积是表示平面中二维图形或形状或平面层的程度的数量。

表面积是三维物体的二维表面上的模拟物。

面积可以理解为具有给定厚度的材料的量，面积是形成形状的模型所必需的。

这里给大家分享一些三年级数学面积知识点，欢迎阅读!三年级数学面积知识点1、物体的表面或封闭图形的大小，就是他们的面积。

2、比较两个图形面积的大小，要用统一的面积单位来测量。

3、常用的面积单位有平方厘米(cm2)，平方分米(dm2)、平方米(m2)。

4、边长1厘米的正方形面积是1平方厘米。

5、边长1分米的正方形面积是1平方分米。

6、边长1米的正方形面积是1平方米。

7、边长100米的正方形面积是1公顷(*****平方米)。

8、边长1千米(1000米)的正方形面积是1平方千米。

9、测量土地的面积时，常常要用到更大的面积单位：公顷、平方千米。

平方千米公顷平方米平方分米平方厘米10、长方形的面积=长×宽长=面积÷宽宽=面积÷长11、正方形的面积=边长×边长12、长方形的周长=(长+宽)×2宽=周长÷2-长长=周长÷2-宽13、正方形的周长=边长×414、正方形的边长=周长÷415、相邻的两个常用的长度单位间的进率是10。

16、相邻的两个常用的面积单位间的进率是100。

17、1平方米=100平方分米;1平方分米=100平方厘米;1公顷=*****平方米;1平方千米=100公顷(公顷、平方千米这两个土地面积单位间的进率是100。

)注：面积和周长是不能相比较的;分清楚什么时候填长度单位，什么时候填面积单位，填土地面积单位时，比较小的土地面积(如：公园、体育场馆、超市、果园、广场)等一般情况下填公顷;(城市的占地、国家的面积、江河湖海的面积)等一般情况下填平方千米。

面积相等的两个图形，周长不一定相等。

注意：周长相等的两个图形，面积不一定相等。

《面积》知识点归纳
知识点一、面积的概念
1、物体的表面或围成的平面图形的大小，叫做它的面积。

2、常用面积单位有平方厘米、平方分米、平方米，可以分别用字母写作为：cm2、dm2、m2。

3、1平方厘米、1平方分米、1平方米的定义：
①边长为1厘米的正方形，面积是1平方厘米。

②边长为1分米的正方形，面积是1平方分米。

③边长为1米的正方形，面积是1平方米。

4、1平方厘、1平方分米、1平方米在实际生活中有多大：
①1平方厘米大约是一只手指的指甲的面积。

②1平方分米大约是一盒粉笔盒的底面面积。

③1平方米大约是一张书桌的桌面面积。

知识点二、周长与面积
1、环绕封闭图形边缘一周的长度，叫做它的周长。

2、周长和面积的公式如下：
3、长度单位用来测量物体的长短，面积单位用来测量物体的面的大小，它们是不同类型的单位，无法比较大小。

4、相同类型的单位要比较大小，应该把单位化成完全相同，再比较。

5、单位转换：
长度单位：
①1米=10分米，1分米=10厘米，1厘米=10毫米。

相邻两个常用的长度单位的进率是10 。

②1米=100厘米。

1千米=1000米。

面积单位：
①1平方米=100平方分米，1平方分米=100平方厘米，相邻两个常用的面积单位的进率是100 。

②1平方米=10000平方厘米。

6、大单位转化为小单位，要乘以进率；小单位转化为大单位，要除以进率。

7、周长相等的两个图形，面积不一定相等；面积相等的两个图形，周长也不一定相等。

三年级数学下册第五单元《认识面积》一、引言在数学学科中，面积是一个非常重要的概念。

在我们日常生活中，我们经常会遇到各种各样的物体，比如桌子、地板、房间等等，这些物体都有一个共同的特征，就是它们都有面积。

通过学习认识面积，我们可以更好地了解物体的大小、形状以及它们之间的关系。

二、什么是面积？面积是指一个物体所占据的平面空间的大小。

我们可以把面积理解为物体的“表面积”。

用数学术语来说，面积是指平行于底面的所有点所组成的平面图形的大小。

三、面积的单位在计算面积时，我们需要使用一定的单位来表示。

常见的面积单位有平方米（m2）、平方厘米（cm2）和平方英尺（ft^2）等。

平方米是国际单位制中的面积单位，在我们的生活中应用非常广泛。

四、如何计算面积？要计算一个物体的面积，我们需要知道它的形状。

不同的形状有不同的计算方法。

下面我们来介绍一些常见的图形的面积计算方法。

1. 正方形和矩形的面积计算正方形和矩形的面积计算方法非常简单，只需要知道它们的边长和宽度，并将它们相乘即可。

即面积 = 边长 × 宽度。

2. 三角形的面积计算三角形的面积计算稍微复杂一些，需要使用三角形的底边长度和高度来计算。

具体的计算公式是：面积 = 底边长度 × 高度 / 2。

3. 圆形的面积计算圆形的面积计算需要用到圆的半径。

圆的面积计算公式是：面积= π × 半径^2，其中π是一个常数，约等于3.14159。

五、应用实例1. 计算房间的面积假设我们要计算一间房间的面积，首先我们需要测量房间的长度和宽度，然后将长度和宽度相乘，即可得到房间的面积。

2. 计算花坛的面积假设我们要计算一个圆形花坛的面积，我们需要测量花坛的半径，然后使用圆的面积公式计算即可。

六、总结通过学习认识面积，我们可以更好地理解物体的大小、形状以及它们之间的关系。

面积是一个非常有用的概念，在日常生活中有着广泛的应用。

通过计算面积，我们可以知道一个物体有多大，从而方便我们做出一些决策。

比较图形面积大小的方法
问题导入比一比哪个图形的面积大？
方法讲解
1．理解题意
两个图形，第一个图形是正方形，第二个图形是长方形。

要求比较正方形和长方形的面积的大小。

通过知识点一的学习，我们知道，如果两个图形的面积差异较大，用观察法就可以直接看出哪个面积大，哪个面积小；如果两个图形的形状不一样，面积相差又不大，就不能用观察法直接看出哪个面积大，哪个面积小，因此要采用其他方法比较。

2．探究比较方法
方法一重叠法。

方法说明：此方法是先把两个图形沿边缘对齐重叠，然后把不重叠的部分剪下来，再把余下的部分重叠，把不重叠的部分剪下来，再重叠……直至拼到两个图形没有可重叠的部分为止，那么哪个图形有剩余，那个图形的面积就大。

操作演示：
结论：把两个图形剪拼后发现，正方形的面积大。

方法二数格法。

方法说明：此方法是在每个图形里画出边长相同的格子。

在哪个图形里画出这样的格子多，那个图形的面积就大。

数格法是比较图形面积大小的基本方法。

要注意使用这种方法的条件是图形上格子的大
小必须统一。

操作演示：
结论：正方形里有16个格子，而长方形里有15个格子，所以正方形的面积大。

归纳总结
比较两个图形面积大小的方法：(1)观察法；(2)重叠法；(3)数格法。

无论采用哪种方法比较，同一种方法中选择的标准必须统一。

【大单元教材解读】小学数学三年级下册第五单元《面积》本单元教学内容，是在学生已经掌握了长方形和正方形的特征，并会计算长方形和正方形周长的基础上进行的。

主要内容包括四部分：面积和面积单位，长方形、正方形的面积计算，面积单位之间的进率，用所学的知识解决简单的实际问题。

通过这部分内容的学习，不仅有利于发展学生的空间观念，提高解决简单实际问题的能力，为以后学习其他平面图形的面积计算打下基础；而且有利于学生把握度量的数学结构，为体积及其他相关内容的学习奠定基础。

《义务教育数学课程标准（2022年版）》在“学段目标”的“第一学段”中提出：“理解常见的量”“了解分析问题和解决问题的一些基本方法，知道同一个问题可以有不同的解决方法”。

《义务教育数学课程标准（2022年版）》在“课程内容”的“第一学段”中提出“结合实例认识面积，体会并认识面积单位厘米2、分米2、米2，能进行简单的单位换算”“探索并掌握长方形、正方形的面积公式，会估计给定简单图形的面积”。

01 单元教材分析本单元教学内容，是在学生已经掌握了长方形和正方形的特征，并会计算长方形和正方形周长的基础上进行的。

主要内容包括四部分:面积和面积单位，长方形、正方形的面积计算，面积单位之间的进率，用所学的知识解决简单的实际问题。

通过这部分内容的学习，不仅有利于发展学生的空间观念，提高解决简单实际问题的能力，为以后学习其他平面图形的面积计算打下基础;而且有利于学生把握度量的数学结构，为体积及其他相关内容的学习奠定基础。

02教材编排特点1.注重学生对面积概念的真正理解。

2.注重引导学生体会度量的意义，认识度量单位及实际意义，渗透度量意识。

3.让学生经历探究的过程。

4.注重培养学生的应用意识和实践能力。

03 课标解读及核心素养《义务教育数学课程标准(2022年版)》在“学段目标”的“第一学段”中提出:“理解常见的量”“了解分析问题和解决问题的一些基本方法，知道同一个问题可以有不同的解决方法”。

《面积》知识点一、面积的意义物体的表面或封闭图形的大小，就是他们的面积。

二、长度单位与面积单位的区别用长度单位表示物体的长短或封闭图形一周的长度；用面积单位表示物体表面或封闭图形的大小。

注：面积和周长是不能相比较的；分清楚什么时候填长度单位，什么时候填面积单位。

三、比较两个图形面积的大小要用统一的面积单位来测量和比较。

四、常用的面积单位有平方厘米（cm²）；平方分米（dm²）；平方米（m²）。

1、边长1厘米的正方形面积是1平方厘米。

反过来，面积是1平方厘米的正方形，它的边长是1厘米2、边长1分米的正方形面积是1平方分米。

反过来，面积是1平方分米的正方形，它的边长是1分米3、边长1米的正方形面积是1平方米。

反过来，面积是1平方米的正方形，它的边长是1米五、面积单位间的换算大单位化成小单位，用大单位前面的数乘进率；小单位化成大单位，用小单位前面的数除以进率。

1平方米=100平方分米；1平方分米=100平方厘米六、面积和周长公式长方形的面积=长×宽长=面积÷宽宽=面积÷长正方形的面积=边长×边长长方形的周长=(长+宽)×2宽= 周长÷2-长长=周长÷2-宽正方形的周长=边长×4正方形的边长=周长÷4注意：面积相等的两个图形，它们周长不一定相等。

周长相等的两个图形面积不一定相等。

面积相等的长方形、正方形中，长方形的周长最长；周长相等的长方形、正方形中，正方形面积最大.七、铺地砖问题①先算出所铺地面的总面积；②计算出每块地砖的面积；③将这两个面积统一成相同的面积单位；④地砖的总块数=所铺地面的总面积÷每块地砖的面积《面积》提升练习题一、填空1、长方形的面积＝( )×( )正方形的面积＝( )×( )正方形的周长＝( )×( )2、长方形的长16厘米，宽12厘米，它的周长是( )厘米，面积是( )平方厘米。

三年级数学下册第五单元《面积》知识点面积和面积单位1.常用的面积单位有：（平方厘米）、（平方分米）、（平方米）。

2.理解面积的意义和面积单位的意义。

面积：物体表面或封闭图形的大小，叫做它们的面积。

1平方米：边长是1米的正方形，它的面积是1平方米。

1平方分米：边长是1分米的正方形，它的面积是1平方分米。

1平方厘米：边长是1厘米的正方形，它的面积是1平方厘米。

3.在生活中找出接近于1平方厘米、1平方分米、1平方米的例子。

例如1平方厘米（指甲盖）、1平方分米（电脑光盘或电线插座）、1平方米（教室侧面的小展板）。

4．区分长度单位和面积单位的不同。

长度单位测量线段的长短，面积单位测量面的大小。

5．比较两个图形面积的大小，要用（统一）的面积单位来测量。

【背熟】（1）边长（1厘米）的正方形，面积是（1平方厘米）。

（反过来也要会说。

面积是1平方厘米的正方形，它的边长是1厘米。

）（2）边长（1分米）的正方形，面积是（1平方分米）。

（3）边长（1米）的正方形，面积是（1平方米）。

（4）边长是（100米）的正方形面积是（1公顷），也就是（10000平方米）。

（5）边长是（1千米）的正方形面积是1平方千米。

面积单位进率和土地面积单位：1.常用的土地面积单位有（公顷）和（平方千米）。

“公顷”→测量菜地面积、果园面积、建筑面积“平方千米”→测量城市土地面积、国家面积1公顷：边长是100米的正方形，它的面积是1公顷。

1平方千米：边长是1千米的正方形，它的面积是1平方千米。

1公顷=10000平方米1平方千米=100公顷1平方千米=1000000平方米2.正确理解并熟记相邻的面积单位之间的进率。

①进率1001平方米= 100平方分米1平方分米= 100平方厘米1平方千米= 100 公顷②进率100001公顷= 10000平方米1平方米= 10000平方厘米③进率10000001平方千米= 1000000平方米④相邻两个常用的长度单位之间的进率是（10 ）。

三年级数学下册《面积》知识点与专项练习三年级数学下册《面积》知识点1.物体的表面或封闭图形的大小，就是他们的面积。

2.比较两个图形面积的大小，要用统一的面积单位来测量。

3.常用的面积单位有平方厘米(cm2)，平方分米(dm2)、平方米(m2)。

4.边长1厘米的正方形面积是1平方厘米。

5.边长1分米的正方形面积是1平方分米。

6.边长1米的正方形面积是1平方米。

7.边长100米的正方形面积是1公顷(10000平方米)。

8.边长1千米(1000米)的正方形面积是1平方千米。

9.测量土地的面积时，常常要用到更大的面积单位：公顷、平方千米。

平方千米公顷平方米平方分米平方厘米10.长方形的面积=长×宽; 长 = 面积÷宽; 宽 = 面积÷ 长11.正方形的面积=边长×边长12.长方形的周长=(长+宽)×2;宽 = 周长÷2-长; 长 = 周长÷2-宽13.正方形的周长=边长×414.正方形的边长=周长÷415.相邻的两个常用的长度单位间的进率是10。

16.相邻的两个常用的面积单位间的进率是100。

17.1平方米=100平方分米 ;1平方分米=100平方厘米;1公顷=10000平方米;1平方千米=100公顷(公顷、平方千米这两个土地面积单位间的进率是100。

)注：面积和周长是不能相比较的;分清楚什么时候填长度单位，什么时候填面积单位，填土地面积单位时，比较小的土地面积(如：公园、体育场馆、超市、果园、广场)等一般情况下填公顷;(城市的占地、国家的面积、江河湖海的面积)等一般情况下填平方千米。

注意：① 面积相等的两个图形，周长不一定相等。

②周长相等的两个图形，面积不一定相等。

三年级下册数学面积应用题专项练习1. 一个长方形的长是15厘米，宽是4厘米，这个长方形的周长和面积各是多少?2. 一个小正方形的边长是3厘米，一个大正方形的边长是小正方形边长的4倍，大正方形的面积是多少?3. 一根36米的绳子围成一个正方形，这个正方形的面积是多少?4. 一个长方形的周长是120分米，长是36分米，求长方形的面积?5. 有一块长方形菜地，它较长的一条边靠着墙，长20米，用篱笆将这个菜地围起来要40米。

三年级下册《面积》知识点归纳1、认识面积2、认识面积单位：平方米(m2) 平方分米(dm2) 平方厘米(cm2)3、计算长方形、正方形的面积: 长方形的面积= 长宽正方形的面积= 边长边长4、面积单位的换算: 1分米2 = 100 厘米21米2 = 100分米21公顷= 10000米21千米2 = 1000000米21千米2 = 100公顷什么是面积(认识面积)1、通过学生参与画图活动，认识图形面积的含义。

2.经历比较两个图形面积大小的过程，体验比较策略的多样性。

3.在活动中培养学生的动手操作能力、分析综合能力和初步的空间观念以及与人合作交流的能力。

量一量1引导学生探索长方形面积计算公式，初步理解长方形和正方形面积的计算方法，会正确地计算长方形和正方形的面积。

2.引导学生估计给定的长方形、正方形面积，培养学生的空间观念和几何直观能力。

3.经历数学知识的应用过程，感受身边的数学，体验学数学、用数学的乐趣。

摆一摆(长方形、正方形的面积)1、引导学生探索长方形面积计算公式，初步理解长方形和正方形面积的计算方法，会正确地计算长方形和正方形的面积。

2.引导学生估计给定的长方形、正方形面积，培养学生的空间观念和几何直观能力。

3.经历数学知识的应用过程，感受身边的数学，体验学数学、用数学的乐趣。

铺地面(面积单位的换算)1、结合解决问题的具体情境，体会面积单位换算和使用大的面积单位的必要性。

唐宋或更早之前，针对“经学”“律学”“算学”和“书学”各科目，其相应传授者称为“博士”，这与当今“博士”含义已经相去甚远。

而对那些特别讲授“武事”或讲解“经籍”者，又称“讲师”。

“教授”和“助教”均原为学官称谓。

前者始于宋，乃“宗学”“律学”“医学”“武学”等科目的讲授者；而后者则于西晋武帝时代即已设立了，主要协助国子、博士培养生徒。

“助教”在古代不仅要作入流的学问，其教书育人的职责也十分明晰。

唐代国子学、太学等所设之“助教”一席，也是当朝打眼的学官。