湛江师院附中2019学年高三年级第六次月考数学(理科)试卷

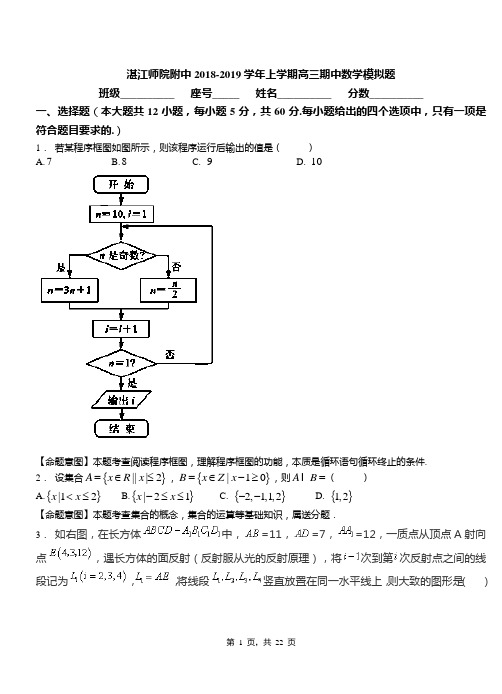
湛江师院附中2018-2019学年上学期高三期中数学模拟题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 若某程序框图如图所示，则该程序运行后输出的值是（ ） A.7B.8C. 9D. 10【命题意图】本题考查阅读程序框图，理解程序框图的功能，本质是循环语句循环终止的条件. 2． 设集合{}|||2A x R x =∈≤，{}|10B x Z x =∈-≥，则A B =（ ）A.{}|12x x <≤B.{}|21x x -≤≤C. {}2,1,1,2--D. {}1,2【命题意图】本题考查集合的概念，集合的运算等基础知识，属送分题． 3． 如右图，在长方体中，=11，=7，=12，一质点从顶点A 射向点，遇长方体的面反射（反射服从光的反射原理），将次到第次反射点之间的线段记为，，将线段竖直放置在同一水平线上，则大致的图形是（ ）ABCD4． 已知实数y x ,满足不等式组⎪⎩⎪⎨⎧≤-≥+≤-5342y x y x x y ，若目标函数mx y z -=取得最大值时有唯一的最优解)3,1(，则实数m 的取值范围是（ ）A ．1-<mB ．10<<mC ．1>mD ．1≥m【命题意图】本题考查了线性规划知识，突出了对线性目标函数在给定可行域上最值的探讨，该题属于逆向问题，重点把握好作图的准确性及几何意义的转化，难度中等.5． 已知全集R U =，集合{|||1,}A x x x R =≤∈，集合{|21,}xB x x R =≤∈，则集合U AC B 为（ ）A.]1,1[-B.]1,0[C.]1,0(D.)0,1[- 【命题意图】本题考查集合的运算等基础知识，意在考查运算求解能力.6． 已知,A B 是球O 的球面上两点，60AOB ∠=︒，C 为该球面上的动点，若三棱锥O ABC -体积的最大值为O 的体积为（ ）A ．81πB ．128πC ．144πD ．288π【命题意图】本题考查棱锥、球的体积、球的性质，意在考查空间想象能力、逻辑推理能力、方程思想、运算求解能力．7． 过抛物线22(0)y px p =>焦点F 的直线与双曲线2218-=y x 的一条渐近线平行，并交其抛物线于A 、 B 两点，若>AF BF ，且||3AF =，则抛物线方程为（ ）A ．2y x =B ．22y x =C ．24y x =D ．23y x =【命题意图】本题考查抛物线方程、抛物线定义、双曲线标准方程和简单几何性质等基础知识，意在考查方程思想和运算能力． 8． 若集合,则= ( )ABC D9． 某三棱锥的三视图如图所示，该三棱锥的体积是（ ） A ． 2 B ．4 C ．34 D ．38【命题意图】本题考查三视图的还原以及特殊几何体的体积度量，重点考查空间想象能力及对基本体积公式的运用，难度中等.10．执行如图所示的程序，若输入的3x =，则输出的所有x 的值的和为（ ） A ．243 B ．363 C ．729 D ．1092【命题意图】本题考查程序框图的识别和运算，意在考查识图能力、简单的计算能力．11．已知函数f （x ）＝⎩⎪⎨⎪⎧log 2（a －x ），x ＜12x ，x ≥1若f （－6）＋f （log 26）＝9，则a 的值为（ ）A ．4B ．3C ．2D ．112．若复数12,z z 在复平面内对应的点关于y 轴对称，且12i z =-，则复数12z z 在复平面内对应的点在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【命题意图】本题考查复数的几何意义、代数运算等基础知识，意在考查转化思想与计算能力．二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知()f x 是定义在R 上函数，()f x '是()f x 的导数，给出结论如下： ①若()()0f x f x '+>，且(0)1f =，则不等式()x f x e -<的解集为(0,)+∞； ②若()()0f x f x '->，则(2015)(2014)f ef >； ③若()2()0xf x f x '+>，则1(2)4(2),n n f f n N +*<∈；④若()()0f x f x x'+>，且(0)f e =，则函数()xf x 有极小值0； ⑤若()()xe xf x f x x'+=，且(1)f e =，则函数()f x 在(0,)+∞上递增．其中所有正确结论的序号是 ．14．若函数63e ()()32ex x bf x x a =-∈R 为奇函数，则ab =___________． 【命题意图】本题考查函数的奇偶性，意在考查方程思想与计算能力．15．已知,x y 满足41y xx y x ≥⎧⎪+≤⎨⎪≥⎩，则22223y xy x x -+的取值范围为____________. 16．设,则三、解答题（本大共6小题，共17．（本小题满分14分） 已知函数()ln kf x x x x=-（k R ∈），其图象与x 轴交于不同两点1(,0)A x ，2(,0)B x ，且12x x <. （1）求实数k 的取值范围； （2）证明：1121222e x x e --<+<.18．（本小题满分12分）已知1()2ln ()f x x a x a R x=--∈． （Ⅰ）当3a =时，求()f x 的单调区间；（Ⅱ）设()()2ln g x f x x a x =-+，且()g x 有两个极值点，其中1[0,1]x ∈，求12()()g x g x -的最小值．【命题意图】本题考查导数的应用等基础知识，意在考查转化与化归思想和综合分析问题、解决问题的能力．19．（本小题满分10分）选修4-1：几何证明选讲1111]如图，点C 为圆O 上一点，CP 为圆的切线，CE 为圆的直径，3CP =.（1）若PE 交圆O 于点F ，165EF =，求CE 的长； （2）若连接OP 并延长交圆O 于,A B 两点，CD OP ⊥于D ，求CD 的长.20．（14分）已知函数1()ln ,()e x x f x mx a x m g x -=--=，其中m ，a 均为实数．（1）求()g x 的极值； 3分（2）设1,0m a =<，若对任意的12,[3,4]x x ∈12()x x ≠，212111()()()()f x f xg x g x -<-恒成立，求a 的最小值； 5分（3）设2a =，若对任意给定的0(0,e]x ∈，在区间(0,e]上总存在1212,()t t t t ≠，使得120()()()f t f t g x == 成立，求m 的取值范围． 6分21．（本小题满分13分）如图，已知椭圆22:14x C y +=的上、下顶点分别为,A B ，点P 在椭圆上，且异于点,A B ，直线,AP BP 与直线:2l y =-分别交于点,M N ，（1）设直线,AP BP 的斜率分别为12,k k ，求证：12k k ⋅为定值； （2）求线段MN 的长的最小值；（3）当点P 运动时，以MN 为直径的圆是否经过某定点？请证明你的结论．【命题意图】本题主要考查椭圆的标准方程及性质、直线与椭圆的位置关系，考查考生运算求解能力，分析问题与解决问题的能力，是中档题.22．（本小题满分10分）选修4-1：几何证明选讲．如图，AB 是⊙O 的直径，AC 是⊙O 的切线，BC 交⊙O 于E ，过E 的切线与AC 交于D .（1）求证：CD ＝DA ；（2）若CE ＝1，AB ＝2，求DE 的长．湛江师院附中2018-2019学年上学期高三期中数学模拟题（参考答案）一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 【答案】A【解析】运行该程序，注意到循环终止的条件，有n =10，i =1；n =5，i =2；n =16，i =3；n =8，i =4；n =4，i =5；n =2，i =6；n =1，i =7，到此循环终止，故选 A. 2． 【答案】D【解析】由绝对值的定义及||2x ≤，得22x -≤≤，则{}|22A x x =-≤≤，所以{}1,2A B =，故选D.3． 【答案】C 【解析】根据题意有：A 的坐标为：（0，0，0），B 的坐标为（11，0，0），C 的坐标为（11，7，0），D 的坐标为（0，7，0）； A 1的坐标为：（0，0，12），B 1的坐标为（11，0，12），C 1的坐标为（11，7，12），D 1的坐标为（0，7，12）；E 的坐标为（4，3，12） （1）l 1长度计算 所以：l 1=|AE|==13。

2019-2020学年广东省湛江市师范附属中学高三数学文模拟试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知直线、、不重合，平面、不重合，下列命题正确的是（）A．若，，，则 B．若，，则 C．若，则 D．若，则参考答案：D略2. 某三棱锥的三视图如图所示，则该三棱锥最长的棱的棱长为( )A. 3B.C.D. 2参考答案：A由三视图可得几何体的直观图如图所示：有：面ABC，△ABC中，，边上的高为2，所以.该三棱锥最长的棱的棱长为.故选A.点睛; 思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.3. 已知直线平行，则实数的值为（）．A． B． C．或D．参考答案：A4. 已知tanα=2（α∈（0，π）），则cos（+2α）=（）A．B．C．﹣D．﹣参考答案：D【考点】二倍角的余弦．【专题】转化思想；综合法；三角函数的求值．【分析】由条件利用诱导公式、二倍角的正弦公式、同角三角函数的基本关系，求得cos（+2α）的值．【解答】解：∵tanα=2，α∈（0，π），则cos（+2α）=cos（+2α）=﹣sin2α=﹣2sinαcosα=﹣=﹣═=﹣，故选：D．【点评】本题主要考查诱导公式、二倍角的正弦公式、同角三角函数的基本关系的应用，属于基础题．5. 若函数,则对于不同的实数,则函数的单调区间个数不可能是( )A.1个B. 2个C.3个D.5个参考答案：B6. 某空间几何体的三视图如右图所示，则该几何体的表面积为A. B. C. D.参考答案：B7. 一个空间几何体的三视图如下左图所示，则该几何体的表面积为A．48 B．48+8 C．32+8 D．80参考答案：B8. 设0<x<，则“xsin2x<1”是“xsin x<1”的( )(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件参考答案：B9. 设曲线在点处的切线与直线垂直，则（）A. 2B.C.D.参考答案：B略10. 如图E、F是正方形ABCD两边的三等分点，向正方形ABCD内任投一点M，记点M落在阴影区域的概率为p，则a=p是函数y=ax2+2x+1有两个零点的（）A．充分不必要条件B．必要不充分条件C．充要条件D．非充分非必要条件参考答案：A考点：必要条件、充分条件与充要条件的判断；函数零点的判定定理．专题：简易逻辑．分析：求出概率p，结合函数零点的关系以及成充分条件和必要条件的定义进行判断即可．解答：解：∵E、F是正方形ABCD两边的三等分点，∴向正方形ABCD内任投一点M，记点M落在阴影区域的概率为p=，若函数y=ax2+2x+1有两个零点，则判别式△=4﹣4a≥0，即a≤1，则a=p是函数y=ax2+2x+1有两个零点的充分不必要条件，故选：A点评：本题主要考查充分条件和必要条件的判断，根据概率的计算以及函数零点的关系是解决本题的关键．二、填空题:本大题共7小题,每小题4分,共28分11. 函数的图象如图所示，则的值为．参考答案：12. 已知双曲线的离心率，则一条渐近线与实轴所成锐角的值是_______．参考答案：略13. 若函数f（x）在定义域D内某区间I上是增函数，且在I上是减函数，则称y=f（x）在I 上是“弱增函数”．已知函数h（x）=x2﹣（b﹣1）x+b在（0，1]上是“弱增函数”，则实数b的值为．参考答案：1略14. 直线y＝－x＋b与5x＋3y－31＝0的交点在第一象限，则b的取值范围是________．参考答案：略15. 定义在R上的函数f（x）满足：f（2）=1，且对于任意的x∈R，都有f′（x）＜，则不等式f（log2x）＞的解集为．参考答案：{x丨0＜x＜4}【考点】利用导数研究函数的单调性；指、对数不等式的解法．【分析】构造辅助函数，求导，由题意可知F（x）=f（x）﹣x在R单调递减，原不等式转化成F（log2x）＞F（2），（x＞0），根据函数的单调性即可求得不等式的解集．【解答】解：设F（x）=f（x）﹣x，求导F′（x）=f′（x）﹣＜0，则F（x）在R单调递减，由f（log2x）＞，即f（log2x）﹣?log2x＞，由f（2）﹣×2=，∴F（log2x）＞F（2），（x＞0），则log2x＜2，解得：0＜x＜4，∴不等式的解集为：{x丨0＜x＜4}，故答案为：：{x丨0＜x＜4}．故答案为：{x丨0＜x＜4}．【点评】本题考查导数的综合应用，考查利用导数求函数的单调性，考查转化思想，属于中档题．16. 已知，，，则的最小值是．参考答案：417. 已知x，y为正实数，且满足4x＋3y＝12，则xy的最大值为________．参考答案：3略三、解答题：本大题共5小题，共72分。

2019届高三全国大联考月考试卷数学（理科）时臺：120分钟满分：150分一、选择题：本大题共12小题，每小题5分，共60分，在每小题的四个选项中，只有 一项是符合题目要求的.1 -设复数z=x+yi ，其中x ，y 是实数，i 是虚数单位，若亡=%+i ，则复数z 的共辘 复数在复平面内对应的点位于（）A •第一象限B.第二象限 C •第三象限 D.第四象限JI2 •已知向量a 与b 的夹角是了,且|创=1，|创=4，若Qa+Ab ）J.a ，则实数久的值为（B ）A 3门3小2小 2 A ，2 B. —2 C 亍D. —j 3 •下列说法中正确的是（）A •若样本数据兀I ，x 2，…，x “的平均数为5，则样本数据2X| + 1，2X 2+12x fl +］ 的平均数为10B •用系统抽样法从某班按学号抽取5名同学参加某项活动，若抽取的学号为5，16，27， 38，49，则该班学生人数可能为60C •某种圆环形零件的外径服从正态分布N （4，0.25）（单位：cm ），质检员从某批零件屮随 机抽取一个，测得其外径为5.6 cm ，则这批零件不合格D ・对某样本通过独立性检验，得知有95%的把握认为吸烟与患肺病有关系，则在该样 本吸烟的人群中有95%的人可能患肺病 A ・ _84C • -245.已知函数ZU ）是定义在R 上的奇函数，且./W 在R 上单调递增 喏a ，b ，c 成等差数列， 且b ＞0，则下列结论正确的是（）A ・〃）＞（），且/（a ）+j （c ）＞0B ・弘）＞0，且C ・."）＜0,且.他/）+张）＞0D •妙＜0，且 fia ）+f （c ）＜06 •设x 为区间［—2，2］内的均匀随机数，则计算机执行下列程序后，输出的y 值落在区 INPUT A ：IF x<=0 THENy=2 xELSEEND IFPRINT yEND C.£ D.1间㊁，3内的概率为（）1B. D. 8424A 3 厂5 J " A4 B-8 C2 D-87・已知函数Xx） = sin2x-2sin2x+l 给出下列四个结论：（）①两数./U ）的最小正周期是2 JI ；②函数./U ）在区间+，斗上是减函数；③函数./U ）的兀— L 兀图象关于直线■对称；④函数./U ）的图象可由函数y=yj2s'm 2x 的图象向左平移才个单位 得到.其中正确结论的个数是A • 1 B. 2C - 3 D. 48.已知命题/?：若a>2Rb>2 » WJ a+b<ab ；命题q ： |无>0，使（兀一 1）公=1，则下列 命题中为真命题的是（A ）A • pf\q B.（絲 p ）/\qC ・〃/\（綁 g ） D.（綁 “）A （綁 q ）9 •己知实数兀，y 满足W +，则z=2|x| —创的最大值为（）A - 5 B. 4C - 3 D. 210 •如图，在平面四边形A BCD 中，AB=AD=CD=] » AB1AD ，BD 丄CD 将该四边形 沿对角线3D 折成一个直二面角A-BD-C ，则四面体ABCD 的外接球的体积为（）A 净B.》C • 2 JI D. 3H2 ?11 -设双曲线升一”=l （Q>0，b>0）的左、右焦点分别为尺，F 2，0为坐标原点，若双曲 线上存在点M 满足\MF ｝\ = 2\MO\=2\MF 2\，则双曲线的离心率为（）A - 6 B. 3 C.V6 D 萌12 •对于给定的正整数n ，设集合乙=｛ 1，2，3，…r ｝，A ，且AH •记/（A ） 为集合A 中的最大元素，当4取遍X”的所有非空子集时，对应的所有/（A ）的和记为SS ），则 S （2 018）=（）A ・ 2 018X22018+l B. 2 （）18X220I 7+1C ・ 2 017X220,7+l D. 2 017X220,8+lm 的值为_・15 •已知函数fiix ） = \2x —l\—a ，若存在实数兀|，兀2（七工兀2），使得/（兀1）=几丫2）= — 1，则a 的取值范围是_（1，2）_ •16・设数列｛為｝的前n 项和为已知心=1，且5=4—（1+令讪詁），则数列｛如 的通项公式是a n = _____________ .三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17〜21题为必 考题，每个试题考生都必须作答.第22，23题为选考题，考生根据要求作答.（—）必考题：60分.17・（本小题满分12分）如图，在平面四边形 ABCD 中，AB=4，AD=2，ZBAD=60° ，ZBC£>= 120° .⑴若BC=2也，求ZCBD 的大小；二、填空题，本大题共4小题，每小题5分，共20分.1 13 •已知14 亍，则 •如图，在△4BC 中，AD=jDC ，P 是线段BD 上一点，^AP=mAB+^AC ，则实数（2）设△BCD的面积为S，求S的取值范围.18・(本小题满分12分)如图，在三棱锥P-ABC中，明丄底面ABC ^AB=2，AC=4，ZBAC=\20°，D为BC 的中点.(1)求证：AD±PB；(2)若二面角A — PB—C的大小为45°‘求三棱锥P-ABC的体积.19•(本小题满分12分)有甲、乙两家外卖公司，其送餐员的FI工资方案如下：甲公司底薪80元，送餐员每单抽成4元；乙公司无底薪，40单以内(含40单)的部分送餐员每单抽成6元，超过40单的部分送餐员侮单抽成7元.现从这两家公司各随机选取一名送餐员分别记录其50天的送餐单数，得到如下频数分布表：(1)从记录甲公司的50天送餐单数中随机抽取3天，求这3天的送餐单数都不小于40单的概率；(2)假设同一个公司的送餐员一天的送餐单数相同，将频率视为概率，回答下列两个问题:(i )求乙公司送餐员日工资的分布列和数学期望；(ii)小张打算到甲、乙两家公司中的一家应聘送餐员，如果仅从日均工资的角度考虑，小张应选择哪家公司应聘？说明你的理由.20•(本小题满分12分)'-2 , 已知椭圆C：孑+”=l(a>b>0)的一个焦点与抛物线)?=4萌兀的焦点重合，且直线y=- x与圆?+/- 10x+20=0 相切.(1)求椭圆C的方程；(2)设斜率为£ II不过原点的直线/与椭圆C相交于4、B两点，0为坐标原点，直线Q4，OB的斜率分别为，k2，若k「k，他成等比数列，推断|OAF + |OB|2是否为定值？若是，求出此定值；若不是，说明理由.21•(本小题满分12分)已知函数/!>)=『一a(x—l)，Q UR，e为自然对数的底数.(1)若存在x o e(l，+oo)，使心0)<0，求实数a的取值范圉; ⑵若夬兀)有两个不同零点X\ 'X2y证明：X\+X2>X\X2.（二）选考题：共10分•请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分.22•（本小题满分10分）选修4—4：坐标系与参数方程在平而直角坐标系xOy屮、以坐标原点O为极点，x轴正半轴为极轴、建立极坐标系、已知曲线G的极坐标方程为/?=4cos°，直线/的参数方程为S （r为参数）.（1）求曲线G的直角坐标方程及直线/的普通方程；%—2cos a ‘JX （2）若曲线C2的参数方程为（«为参数），点P在曲线C】上，其极角为莎‘y=sin a q点Q为曲线C2上的动点，求线段PQ的中点M到直线I的距离的最大值.23•（本小题满分10分）选修4—5：不等式选讲已知函数fix）=\x+a\ + \x~2\，其中d为实常数.⑴若函数7U）的最小值为3，求a的值；（2）若当兀丘［1 » 2］时，不等式4|恒成立»求d的取值范围.。

2019年广东省高考数学真题（理科）及答案一、选择题：本大题共8小题，每小题5分，满分40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合M={x∣x2+2x=0,x∈R},N={x∣x2-2x=0,x∈R},则M∪N=A. {0}B. {0，2}C. {-2,0} D {-2,0,2}2.定义域为R的四个函数y=x3,y=2x,y=x2+1,y=2sinx中，奇函数的个数是A. 4B.3C. 2D.13.若复数z满足iz=2+4i，则在复平面内，z对应的点的坐标是A. （2,4）B.（2,-4）C. (4,-2) D(4,2)4.已知离散型随机变量X的分布列为1 2 3P则X的数学期望E（X）=A. B. 2 C. D 35．某四棱台的三视图如图1所示，则该四棱台的体积是A．4 B． C． D．66．设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是A．若α⊥β，m α，nβ，则m ⊥ n B．若α∥β，mα，nβ，则m∥nC．若m⊥ n，m α，n β，则α⊥β D．若m α，m∥n，n∥β，则α⊥β7．已知中心在原点的双曲线C的右焦点为F（3，0），离心率等于，则C的方程是A． = 1 B． = 1 C． = 1 D． = 18.设整数n≥4，集合X=｛1，2，3……，n｝。

令集合S=｛（x,y,z）|x，y，z∈X，且三条件x<y<z,y<z<x，z<x<y 恰有一个成立｝，若（x，y，z）和（z，w，x）都在s中，则下列选项正确的是A.（y，z，w）∈s，（x，y，w）SB.（y，z，w）∈s，（x，y，w）∈SC. （y，z，w）s，（x，y，w）∈SD. （y，z，w）s，（x，y，w）S二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分。

必做题（9~13题）9.不等式x2+x-2<0的解集为。

2019年湛师附中高三教学质量检测（六）本试卷分选择题和非选择题两部分，共14页，满分150分．考试用时120分钟．注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考号填写在答题卡上．用2B铅笔将答题卡试卷类型（A）填涂在答题卡上，并在答题卡右上角的“试室号”和“座位号”栏填写试室号、座位号，将相应的试室号、座位号信息点涂黑．2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上．3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答卷上各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效．4．考生必须保持答题卡的整洁，考试结束后，将答卷和答题卡一并交回．第Ⅰ卷选择题（共70分）一、单项选择题：本大题共20小题，每小题2分，共40分。

在每小题给出的四个选项中，只有—项是最符合题目要求的。

图1为2019北京奥运火炬登上珠穆朗玛峰的线路图。

据此完成1题。

图11．下列表述正确的是A．登山线路大体沿宽谷、山脊走向B．登山线路大体沿谷地走向C．C4营地—突击营地段线路的平均坡度最小D．四个营地中的前进营地所在处的大气含氧量最低中国海军两艘驱逐舰和一艘大型补给舰组成的舰队，于2019年12月26日从三亚出发前往亚丁湾、索马里海域实施护航，执行维护国际海运安全的任务。

2019年1月6日开始第一次护航，到2月6日为止，已护航15批次，共对33艘船舶实施了护航。

图2为中国军舰赴索马里海域护航路线图，完成2-4题。

2．中国军舰出发赴索马里海域的路途中，下列现象可能出现在我国的是A ．竹外桃花三两枝，春江水暖鸭先知B ．千里黄云白日曛，北风吹雁雪纷纷C ．接天莲叶无穷碧，映日荷花别样红D ．停车坐爱枫林晚，霜叶红于二月花 3．关于中国海军舰队航行过程中的叙述，比较合理的是A ．三亚日出的时间越来越迟B ．佛山某学校正午的旗杆影子逐渐变长 C. 经过马六甲海峡风急浪高 D ．在北印度洋航行顺风顺水4．中国军舰若要去解救一艘被海盗追踪的船只，需要利用的地理信息技术主要是 A ．RS GIS B ．GPS GIS C ．GIS SOS D ．SOS GPS 5．图3所示河流以雨水补给为主，该河流可能出现在A ．35°N —55°N 大陆东岸B ．30°S —40°S 大陆西岸C ．25°N —35°N 大陆东岸D ．10°S —20°S 大陆内部6．全球变暖，使世界上的一些主要河流正面临日益严重的干涸危险，下列叙述错误．．的是 A ．全球变暖加快冰川融化，对内陆地区的河流影响最大 B ．全球变暖对赤道地区的河流影响比较小C ．全球变暖近期对一些主要河流的下游将易引发洪涝灾害D ．全球变暖对分布在中纬度的河流影响不大图4为2019年3月3日—7日天气预报图（来源：南海气象局），读图完成第7题。

2019年广东省高考数学真题（理科）及答案一、选择题：本大题共8小题，每小题5分，满分40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合M={x∣x2+2x=0,x∈R},N={x∣x2-2x=0,x∈R},则M∪N=A. {0}B. {0，2}C. {-2,0} D {-2,0,2}2.定义域为R的四个函数y=x3,y=2x,y=x2+1,y=2sinx中，奇函数的个数是A. 4B.3C. 2D.13.若复数z满足iz=2+4i，则在复平面内，z对应的点的坐标是A. （2,4）B.（2,-4）C. (4,-2) D(4,2)4.已知离散型随机变量X的分布列为1 2 3P则X的数学期望E（X）=A. B. 2 C. D 35．某四棱台的三视图如图1所示，则该四棱台的体积是A．4 B． C． D．66．设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是A．若α⊥β，m α，nβ，则m ⊥ n B．若α∥β，mα，nβ，则m∥nC．若m⊥ n，m α，n β，则α⊥β D．若m α，m∥n，n∥β，则α⊥β7．已知中心在原点的双曲线C的右焦点为F（3，0），离心率等于，则C的方程是A． = 1 B． = 1 C． = 1 D． = 18.设整数n≥4，集合X=｛1，2，3……，n｝。

令集合S=｛（x,y,z）|x，y，z∈X，且三条件x<y<z,y<z<x，z<x<y 恰有一个成立｝，若（x，y，z）和（z，w，x）都在s中，则下列选项正确的是A.（y，z，w）∈s，（x，y，w）SB.（y，z，w）∈s，（x，y，w）∈SC. （y，z，w）s，（x，y，w）∈SD. （y，z，w）s，（x，y，w）S二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分。

必做题（9~13题）9.不等式x2+x-2<0的解集为。

广东省湛江市2019届高三数学模拟测试试题（二）理（含解析）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.1.若复数满足，其中为虚数单位，是的共轭复数，则复数在复平面内对应的点所在的象限是（）A. 一B. 二C. 三D. 四【答案】A【解析】【分析】利用复数的运算法则、共轭复数的定义和几何意义即可得出．【详解】设则即故解a=3,b=4,则复数在复平面内对应的点在第一象限故选：A【点睛】本题考查了复数的运算法则、共轭复数的定义和几何意义，考查计算能力，属于基础题．2.已知全集，则集合的子集个数为（）A. B. C. D.【答案】C【解析】【分析】先求B.再求，求得则子集个数可求【详解】由题=, 则集合,故其子集个数为故选：C【点睛】此题考查了交、并、补集的混合运算及子集个数，熟练掌握各自的定义是解本题的关键，是基础题3.已知实数是给定的常数，函数的图像不可能是（）A. B.C. D.【答案】D【解析】【分析】令m=0,排除D,对函数求导，确定其极值点的正负即可判断.【详解】当m=0,C符合题意，当m≠0>0,设的两根为则<0,则两个极值点异号，则D不合题意，故选:D.【点睛】本题考查函数图像的识别与判断，导数的应用，考查推理能力，是基础题.4.平行四边形中，，则（）A. B. C. D.【答案】B【解析】【分析】将分别表示为向量及的和，利用数量积的定义求值即可【详解】由题则（）（）=故选：B【点睛】本题考查向量数量积的定义和性质，平面向量基本定理，考查运算能力，属于中档题．5.设分别为离心率的双曲线的左、右焦点，分别为双曲线的左、右顶点，以为直径的圆交双曲线的渐近线于两点，若四边形的面积为，则（）A. B. C. D.【答案】A【解析】【分析】由得渐近线方程与圆的方程联立得M坐标，利用四边形面积得a,c的方程求解即可得b【详解】由题,故渐近线方程为以为直径的圆的方程为，联立，得y=,由双曲线与圆的对称性知四边形为平行四边形，不妨设则四边形的面积S=得ac=,又，得a=1,c=故选：A【点睛】本题考查双曲线的几何性质，圆与直线的交点坐标，考查平行四边形的面积公式，考查计算推理能力，是中档题6.现有甲班四名学生，乙班三名学生，从这名学生中选名学生参加某项活动，则甲、乙两班每班至少有人，且必须参加的方法有（）A. 种B. 种C. 种D. 种【答案】D【解析】【分析】分情况讨论甲乙两个班的人数求解即可【详解】由题按甲乙班参加人数分情况讨论如下：若甲班1人，乙班3人，共1种方法；若甲班2人，乙班2人，共种方法；若甲班3人，乙班1人，共种方法；故甲、乙两班每班至少有人，且必须参加的方法有1+9+9=19种故选：D【点睛】本题考查组合问题，考查分类讨论，讨论要合理全面，计算要准确，是基础题7.在中，内角所对的边分别为，且，则（）A. B. C. D.【答案】A【解析】【分析】根据题目条件结合三角形的正弦定理以及三角形内角和定理可得sin A【详解】∵acosB＝（4c﹣b）cosA．∴sinAcosB＝4sinCcosA﹣sinBcosA即sinAcosB+sinBcosA＝4cosAsinC∴sinC＝4cosAsinC∵0＜C＜π，sinC≠0．∴1＝4cosA，即cosA，则故选：A．【点睛】本题考查了正弦定理，两角和与差的正弦及二倍角公式，熟记公式，准确计算是关键，属于基础题．8.一元线性同余方程组问题最早可见于中国南北朝时期（公元世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：有物不知数，三三数之剩二，五五数之剩三，问物几何？即，一个整数除以三余二，除以五余三，求这个整数.设这个整数为，当时，符合条件的共有（）A. 个B. 个C. 个D. 个【答案】C【解析】【分析】由题设a=3m+2=5n+3,m,n,得3m=5n+1，对m讨论求解即可【详解】由题设a=3m+2=5n+3,m,n,则3m=5n+1当m=5k,n不存在；当m=5k+1，n不存在当m=5k+2,n=3k+1，满足题意当m=5k+3,n不存在；当m=5k+4,n不存在；故2≤a=15k+8≤2019,解,k∈Z,则k=0,1,2…134,共135个故选：C【点睛】本题以传统文化为背景考查整数的运算性质，考查不等式性质，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．9.已知是三个不同的平面，是两条不同的直线，给出下列命题：①若，则；②若，且，则；③若，则；④ ，则.其中真命题的个数是（）A. B. C. D.【答案】C【解析】【分析】利用线面关系逐项分析即可【详解】对①若，则或m,n异面，故错误；对②，由线面平行的判定定理知：若，且，则，正确对③，若，则则，正确对④，设在面内任取点O,作OA OB由，得OA OB故OA OB则又，正确综上真命题的个数是3个故选：C【点睛】本题考查命题真假，考查空间的线面位置关系，熟记定理与性质是关键，是基础易错题10.把函数的图像向左平移个单位长度，再把所得的图像上每个点的横、纵坐标都变为原来的倍，得到函数的图像，并且的图像如图所示，则的表达式可以为（）A. B.C. D.【答案】B【解析】【分析】根据条件先求出φ和ω，结合函数图象变换关系进行求解即可．【详解】∵g（0）＝2sinφ＝1，即sinφ，∴φ或φ（舍去）则g（x）＝2sin（ωx），又当k=1,即g（x）＝2sin（x），把函数g（x）的图象上所有点的横坐标缩短到到原来的，得到y＝2sin（4x），再把纵坐标缩短到到原来的，得到y＝sin（4x），再把所得曲线向右平移个单位长度得到函数g（x）的图象，即g（x）＝sin[（x-）]＝故选：B．【点睛】本题主要考查三角函数图象的应用，根据条件求出ω和φ的值以及利用三角函数图象平移变换关系是解决本题的关键．11.已知直线不过坐标原点，且与椭圆相交于不同的两点的面积为，则的值是（）A. B. C. D. 不能确定【答案】B【解析】【分析】k不存在时, 设直线x=t>0,得A,B坐标进而得k存在时，设直线方程与椭圆联立，由面积公式结合韦达定理化简得，进而得的值即可【详解】由题直线斜率k不存在时，设直线x=t>0，则A(t,), B(t,),S=,解t=则k存在时，设，与椭圆联立得,，点O到直线l的距离d=得，即①又=将①代入得故选：B【点睛】本题考查直线与椭圆的位置关系，韦达定理的应用，面积公式，点在曲线上的代换，考查计算能力，注意斜率不存在的讨论，是中档题12.已知函数，当时，不等式恒成立，则实数的取值范围是（）A. B. C. D.【答案】C【解析】【分析】由题判断为奇函数且单调递增，转化为恒成立，利用单调性得,分离a求导求范围即可【详解】易知单调递增，，则，故为奇函数，当时，不等式恒成立等价为即恒成立，故在时恒成立当x=0时，0恒成立，a当x>0时，,设则设则单增，又，则当0<x<1,当x>1,故即，故单调递增，当x,故，综上故选：C【点睛】本题考查函数的单调性与奇偶性，导数求最值，利用导数研究不等式恒成立问题，考查转化能力，是中档题二、填空题（将答案填在答题纸上）13.已知函数，则曲线在点处的切线方程是_______．【答案】【解析】求导，x=0代入求k，点斜式求切线方程即可【详解】则又故切线方程为y=x+1故答案为y=x+1【点睛】本题考查切线方程，求导法则及运算，考查直线方程，考查计算能力，是基础题14.若实数满足不等式组，且的最小为，则实数______．【答案】【解析】【分析】画出可行域，由z的几何意义确定其最小值，列m的方程求解即可【详解】画出可行域如图阴影部分所示：当过A时取得最小值，联立得A,则，解m=故答案为【点睛】本题考查线性规划，z的几何意义，数形结合思想，确定取得最小值的最优解是关键，15.设，且，则______．【答案】【解析】【详解】故tan又=故，则【点睛】本题考查二倍角公式及两角和与差的正切公式，熟记公式，考查化简能力，是中档题16.圆锥的底面半径为，其侧面展开图是圆心角大小为的扇形.正四棱柱的上底面的顶点均在圆锥的侧面上，棱柱下底面在圆锥的底面上，则此正四棱柱体积的最大值为_____．【答案】【解析】【分析】设圆锥的母线长为l，由侧面展开图求得,进而得圆锥高为，设正四棱柱的底面边长为2a,高为h,进而得，正四棱柱体积V=,设函数=，求导求其最值即可【详解】设圆锥的母线长为l,圆锥底面周长为=圆锥高为设正四棱柱的底面边长为2a,高为h,则得正四棱柱体积V=,设=令得当,故的最大值为故答案为【点睛】本题考查棱柱的体积，圆锥的侧面积公式，正四棱柱的基本性质，利用导数求最值问题，考查空间想象及计算求解能力，是中档题三、解答题（解答应写出文字说明、证明过程或演算步骤.）17.为数列的前项和，已知.（1）求的通项公式；（2）设，求.【答案】（1）（2）【解析】【分析】（1）当时，，检验成立即可求解；（2）由=裂项相消求和即可【详解】（1）当时，当时，满足上式，（2）由可得【点睛】本题考查数列通项公式，裂项相消求和，考查计算能力，熟记求和的基本方法，准确计算是关键，是基础题18.三棱锥中，底面是等腰直角三角形，，且为中点，如图.（1）求证：平面平面；（2）若二面角的大小为，求与平面所成角的正弦值.【答案】（1）见证明；（2）【解析】【分析】（1）证明平面，即可证明平面平面（2）证明为二面角的平面角，得进而得为等边三角形，以为原点，建立空间直角坐标系，求平面的法向量，利用向量的线面角公式求解即可【详解】（1）证明：是等腰直角三角形，为中点，平面平面平面平面（2）平面为二面角的平面角，为等边三角形，以为原点，建立如图所示的空间直角坐标系，则设平面的法向量，则即取设与平面所成角为，则故平面所成角的正弦值为.【点睛】本题考查面面垂直证明，线面垂直的判定及二面角的定义，考查空间向量的线面角求法，考查空间想象及计算求解能力，是中档题19.某小区为了调查居民的生活水平，随机从小区住户中抽取个家庭，得到数据如下：参考公式：回归直线的方程是：，其中，.（1）据题中数据，求月支出（千元）关于月收入（千元）的线性回归方程（保留一位小数）；（2）从这个家庭中随机抽取个，记月支出超过千家庭个数为，求的分布列与数学期望. 【答案】（1）（2）见解析【解析】【分析】（1）先求再利用公式求即可；（2）由超几何分布列分布列求期望即可【详解】（1）所以月支出关于月收入的线性回归方程是：（2）的可能取值为故的分布列为：数学期望. 【点睛】本题考查线性回归方程，考查超几何分布的分布列及期望，考查古典概型，准确计算是关键，是基础题20.已知动圆过定点，且和直线相切，动圆圆心形成的轨迹是曲线，过点的直线与曲线交于两个不同的点.（1）求曲线的方程；（2）在曲线上是否存在定点，使得以为直径的圆恒过点？若存在，求出点坐标；若不存在，说明理由.【答案】（1）（2）见解析【解析】【分析】（1）由抛物线定义确定P 的轨迹方程，（2）设，直线的方程为，代入抛物线方程，整理得设存在定点，由，代入韦达定理整理得，利用即可得【详解】（1）设动圆圆心到直线的距离为，根据题意，动点形成的轨迹是以为焦点，以直线为准线的抛物线，抛物线方程为.（2）根据题意，设，直线的方程为，代入抛物线方程，整理得若设抛物线上存在定点，使得以为直径的圆恒过点，设，则，同理可得解得在曲线上存在定点，使得以为直径的圆恒过点.【点睛】本题考查由定义求轨迹方程，考查直线与抛物线的位置关系，圆的性质的应用，考查计算能力，是中档题21.已知正实数，函数. （1）讨论函数的单调性；（2）若在内有解，求的取值范围.【答案】（1）见解析；（2）【解析】【分析】（1）令，解得,讨论与的大小关系确定的符号变化求单调性即可；（2）在内有解，则，由（1）的讨论确定的正负变化确定其最小值即可求解【详解】令，解得当时，即时在上，函数单调递增，在上，函数单调递减；当时，即时，函数在定义域上单调递增；当时，即时，在上，函数单调递增，在上，函数单调递减.综上所述，当时，在上，函数单调递增；在上，函数单调递减；当时，函数在定义域上单调递增；当时，在上，函数单调递增，在上，函数单调递减.（2）若在内有解，则由（1）可知，当，即时，，函数在上单调递增，，解得；当，即1<a<2时，在时，，函数在上单调递减，在时，，函数在上单调递增，令，函数在上单调递增.恒成立，当，即时，，函数在上单调递减，不成立，综上所述：.【点睛】本题考查导数与函数的单调性，利用导数求函数的最值，分类讨论的思想，考查分析推理能力，是中档题22.选修4-4：坐标系与参数方程在直角坐标系中，点，直线（为参数），以原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.（1）求曲线的直角坐标方程；（2）设直线与曲线交于点，求的值.【答案】（1）（2）【解析】【分析】（1）利用极坐标与普通的互化求解即可；（2）将直线的参数方程化为标准形式为：（为参数），与椭圆联立，利用t的几何意义求解即可【详解】（1）又曲线的直角坐标方程为：（2）将直线的参数方程化为标准形式为：（为参数），代入曲线方程，得.恒成立【点睛】本题考查极坐标与普通方程的互化，考查直线参数方程t 的几何意义，考查计算能力，计算的值注意判断的正负是关键，是中档题23.选修4-5：不等式选讲 已知函数.（1）解不等式； （2）若对于任意恒成立，求实数的最小值，并求当取最小值时的范围. 【答案】（1）（2）【解析】 【分析】（1）零点分段去绝对值化简解不等式即可；（2）恒成立，即恒成立，即，由绝对值三角不等式求即可求解【详解】（1） 当时，不等式化为，解得，可得；当时，不等式化为，解得，可得；当时，不等式化为，解得，可得.综上可得，原不等式的解集为. （2）若恒成立，则恒成立，又最小值为.此时解得.【点睛】本题考查绝对值不等式的解法，绝对值三角不等式求最值，熟记定理，准确计算是关键，绝对值三角不等式成立条件是易错点，是中档题。

2020年广东省湛江市师范学院附属中学高三数学理模拟试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知双曲线两个焦点为分别为，过点的直线与该双曲线的右支交于两点，且是以为直角顶点的等腰直角三角形，则为() A．B．C．D．参考答案：D2. 设集合，则等于A. B. C. D.参考答案：【知识点】交、并、补集的混合运算．A1B 解析：,∴ ,又∵,∴.故选B.【思路点拨】利用集合的并集定义，求出；利用补集的定义求出．3. 极坐标方程表示的曲线为（）A．极点 B．极轴 C．一条直线 D．两条相交直线参考答案：D略4. 设函数其中[x]表示不超过x的最大整数，如[－1.3]＝－2，[1.3]＝1，则函数不同零点的个数为()A．2 B．3 C．4 D．5参考答案：B略5. 在平面直角坐标系中，点在直线的右上方，则的取值范围是A．（1，4）B．（—1，4）C．（—∞，4）D．（4，+∞）参考答案：D试题分析：由题意，．考点：二元一次不等式表示的平面区域．6. 已知集合M={1，2，3，4}，则集合P={x|x∈M，且2x?M}的子集个数为（）A．2 B．3 C．4 D．8参考答案：C【考点】集合中元素个数的最值．【分析】根据题意，写出集合P即可．【解答】解：根据题意，若1∈P，则2×1=2∈M，故不满足题意；若2∈P，则2×2=4∈M，故不满足题意；若3∈P，则2×3=6?M，故满足题意；若4∈P，则2×4=8?M，故满足题意；综上，P={3，4}，所以集合P的子集有：?，{3}，{4}，{3，4}，故选：C．【点评】本题考查集合的定义及子集，属于基础题．7. 设集合，，则( )A． B. C． D.参考答案：C试题分析：，，；故选C．【易错点睛】本题考查利用描述法表示集合以及集合的运算，属于基础题；利用描述法表示集合时，要注意其代表元素的意义，如表示函数的定义域，表示函数的值域，表示函数的图象.考点：1.集合的表示；2.集合的运算．8. 已知，且，则等于A．B．C．D．参考答案：A因为,所以,解得,因为,所以；本题选择A选项.9. 设椭圆的焦点与抛物线的焦点相同，离心率为，则（）A．B． C. D．参考答案：A10. 已知为上的减函数，则满足的实数的取值范围是（）....参考答案：C略二、填空题:本大题共7小题,每小题4分,共28分11. 已知，，则_____________．参考答案：12. 如图，矩形的一边在轴上，另外两个顶点在函数的图象上.若点的坐标，记矩形的周长为，数列的前项和为，则=参考答案：13. 若直线与幂函数的图象相切于点，则直线的方程为___________.参考答案：略14. 是虚数单位，= ▲ .参考答案：15. 设函数y=f（x）的定义域为D，若对于任意的x1，x2∈D，当x1+x2=2a时，恒有f（x1）+f（x2）=2b，则称点（a，b）为函数y=f（x）的对称中心．研究函数f（x）=x+sinπx﹣3的某个对称中心，并利用对称中心的上述定义，可求得f（）+f（））+…+f（）+f（）的值为．参考答案：﹣8058【考点】函数的值．【专题】函数的性质及应用．【分析】由已知得f（x）=x+sinπx﹣3的一个对称中心为（1，﹣2），由此能求出f（）+f（）+f（）+…+f（）+f（）的值．【解答】解：在f（x）=x+sinπx﹣3中，若x1+x2=2，则f（x1）+f（x2）=（x1+x2）+sin（x1π）+sin（x2π）﹣6=2+sin（x1π）+sin（2π﹣x1π）﹣6=﹣4，∴f（x）=x+sinπx﹣3的一个对称中心为（1，﹣2），∴f（）+f（）+f（）+…+f（）+f（）=2014×（﹣4）+f（）=﹣8056+（1+sinπ﹣3）=﹣8058．故答案为：﹣8058．【点评】本题考查函数值的求法，是基础题，解题时要认真审题，注意正弦函数的性质的合理运用．16. 若某算法流程图如右图所示，则该程序运行后输出的B等于．参考答案：63略17. 设U=，A=，若，则实数m=____参考答案：-3三、解答题：本大题共5小题，共72分。

绝密★启用前 试卷类型：A2019届湛师附中(实验学校)高三年级第六次调研考试本试卷共8页，20小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生首先检查答题卡是否整洁无缺损，务必用0.5毫米黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上。

不按要求填涂的，答案无效。

3．非选择题必须用0.5毫米黑色字迹的签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上，请注意每题答题空间，预先合理安排；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再做答。

漏涂、错涂、多涂的答案无效。

5．考生必须保持答题卡的整洁，考试结束后，将答题卡交回。

一、本题共12分，每小题4分，共48分。

在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确，全部选对的得4分，选不全的得2分，有选错或不答的得0分。

1. 分子太小，不能直接观察，我们可以通过墨水的扩散现象来认识分子的运动，在下面所给出的四个研究实例中，采用的研究方法与上述研究分子运动的方法最相似的是 A ．利用磁感线去研究磁场B ．把电流类比为水流进行研究C ．通过电路中灯泡是否发光判断电路中是否有电流D ．研究加速度与合外力．质量间的关系时，先在质量不变的条件下研究加速度与合外力的关系，然后再在合外力不变的条件下研究加速度与质量的关系 2．如图1甲所示，电阻R 的阻值为50Ω，在ab 间加上图1乙所示的正弦交流电，则下面说法中正确的是A ．电阻R 的功率为100WB ．电流表示数为2AC ．产生该交流电的线圈在磁场中转动的角速度为3.14rad/sD ．如果产生该交流电的线圈转速提高一倍，则电流表的示数也增大一倍。