四则运算+运算定律整理与复习
- 格式:ppt
- 大小:1.39 MB
- 文档页数:27


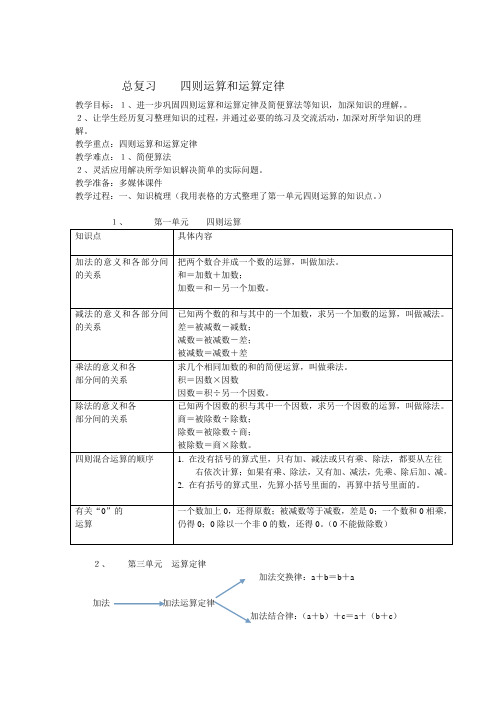
总复习四则运算和运算定律教学目标:1、进一步巩固四则运算和运算定律及简便算法等知识,加深知识的理解,。
2、让学生经历复习整理知识的过程,并通过必要的练习及交流活动,加深对所学知识的理解。
教学重点:四则运算和运算定律教学难点:1、简便算法2、灵活应用解决所学知识解决简单的实际问题。
教学准备:多媒体课件教学过程:一、知识梳理(我用表格的方式整理了第一单元四则运算的知识点。
)1、第一单元四则运算知识点具体内容加法的意义和各部分间的关系把两个数合并成一个数的运算,叫做加法。
和=加数+加数;加数=和-另一个加数。
减法的意义和各部分间的关系已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。
差=被减数-减数;减数=被减数-差;被减数=减数+差乘法的意义和各部分间的关系求几个相同加数的和的简便运算,叫做乘法。
积=因数×因数因数=积÷另一个因数。
除法的意义和各部分间的关系已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
商=被除数÷除数;除数=被除数÷商;被除数=商×除数。
四则混合运算的顺序 1. 在没有括号的算式里,只有加、减法或只有乘、除法,都要从左往右依次计算;如果有乘、除法,又有加、减法,先乘、除后加、减。
2. 在有括号的算式里,先算小括号里面的,再算中括号里面的。
有关“0”的运算一个数加上0,还得原数;被减数等于减数,差是0;一个数和0相乘,仍得0;0除以一个非0的数,还得0。
(0不能做除数)2、第三单元运算定律加法交换律:a+b=b+a加法加法运算定律加法结合律:(a+b)+c=a+(b+c)减法减法的运算性质:a-b-c=a-(b+c)乘法交换律:a×b=b×a 乘法乘法运算定律乘法结合律:(a×b)×c=a×(b×c)乘法分配律:(a+b)×c=a×c+b×c除法除法的运算性质:a÷b÷c=a÷(b×c)二、基础练习1. 在( ) 里填上合适的数,并说一说分别应用了哪些运算定律。

四则运算一、加法的意义和各部分间的关系1.把两个数合并成一个数的运算..................,.叫做加法。
2.加法各部分的名称。
相加的两个数叫做加数;加得的数叫做和。
3.加法各部分间的关系。
和=加数+加数加数=和-另一个加数二、减法的意义和各部分间的关系1.已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。
2.减法各部分的名称。
在减法中,已知的和叫做被减数,其中的一个加数叫做减数,求得的另一个加数叫做差。
3.减法各部分间的关系。
差=被减数-减数减数=被减数-差被减数=减数+差4.减法是加法的逆运算。
5.根据加、减法各部分间的关系可以进行加、减法的验算。
三、乘法的意义和各部分间的关系1.求几个相同加数的和的简便运算...................,.叫做乘法。
2.乘法各部分间的名称。
相乘的两个数叫做因数,乘得的数叫做积。
3.乘法各部分间的关系。
积=因数×因数因数=积÷另一个因数四、除法的意义和各部分间的关系1.已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
2.除法各部分的名称。
在除法中,已知的积叫做被除数,已知的因数叫做除数,求出的未知因数叫做商。
3.没有余数的除法.......各部分间的关系。
商=被除数÷除数除数=被除数÷商被除数=除数×商4.有余数的除法......各部分间的关系。
被除数=商×除数+余数商=(被除数-余数)÷除数除数=(被除数-余数)÷商5.余数一定比除数小。
.........6.除法是乘法的逆运算。
利用乘、除法的互逆关系来验算乘、除法算式。
没有余数的除法算式:五、有关0的运算1.0在运算中的特点。
(1)在加法中,一个数加上0,还得原数。
(2)在减法中,一个数减去0,仍得原数;被减数等于减数,差是0。
(3)在乘法中,一个数和0相乘得0。
(4)在除法中,0除以一个非0的数得0。

四则运算运算定律与简便计算复习教案第一章:四则运算回顾1.1 加法运算:两个数相加得到的结果称为和。
1.2 减法运算:一个数减去另一个数得到的结果称为差。
1.3 乘法运算:两个数相乘得到的结果称为积。
1.4 除法运算:一个数除以另一个数得到的结果称为商。
第二章:运算定律介绍2.1 加法结合律:三个或更多数相加,可以任意改变它们的组合方式,结果不变。
2.2 减法结合律:三个或更多数相减,可以任意改变它们的组合方式,结果不变。
2.3 乘法结合律:三个或更多数相乘,可以任意改变它们的组合方式,结果不变。
2.4 除法结合律:三个或更多数相除,可以任意改变它们的组合方式,结果不变。
第三章:运算定律的应用3.1 加法运算定律的应用:通过改变加数的组合方式,简化计算过程。
3.2 减法运算定律的应用:通过改变减数的组合方式,简化计算过程。
3.3 乘法运算定律的应用:通过改变乘数的组合方式,简化计算过程。
3.4 除法运算定律的应用:通过改变除数的组合方式,简化计算过程。
第四章:简便计算方法4.1 分配律:将一个数与两个数的和相乘,等于将这个数分别与这两个数相乘,将结果相加。
4.2 结合律:在进行乘法或除法运算时,可以任意改变计算的顺序。
4.3 分解法:将一个数分解成两个或多个数的和或差,简化计算过程。
4.4 交换律:在进行加法或乘法运算时,可以任意改变数的顺序。
第五章:综合练习5.1 选择合适的运算定律和简便计算方法,解决实际问题。
5.2 完成一些有关四则运算的练习题,巩固所学的知识。
5.3 进行小组讨论,互相交流解题方法和经验。
第六章:四则运算的顺序6.1 运算顺序规则:在没有括号的算式中,先进行乘除运算,再进行加减运算。
6.2 运算顺序的应用:解决含有多个运算的算式,按照正确的顺序进行计算。
第七章:括号的使用7.1 括号的作用:改变运算顺序,优先计算括号内的运算。
7.2 括号的运用规则:括号前面是加减号时,括号内的运算符号不变;括号前面是乘除号时,括号内的运算符号变相反数。

人教版四年级下册第三单元运算定律的整理与复习设计理念:以学生的发展为本,注重自主学习,小组合作,引导探究,着重培养学生的表述能力,知识的收集整理、归纳分类能力,以及对知识的理解判断与实际运用能力。
教学目标:1.知识与技能:通过整理和复习,使学生形成知识网络,加深对运算定律和性质的理解,能根据算式特点选择合适的运算定律和性质进行简便运算。
感受数学与现实生活的联系,能用所学知识解决简单的实际问题。
2.过程与方法:通过交流、整理、合作、展示、探究,培养学生的表述能力,知识的收集整理、归纳分类能力,以及对知识的理解判断与运用能力,发展思维的灵活性。
3. 情感与态度:激发学生对学习简算技能的意识,感受简算所带来的成功体验,调动互帮互助的学习风气,提高学生学习数学的兴趣。
重点难点重点:整理运算定律和性质难点:合理、灵活地运用运算定律和性质进行简便计算教学准备:课件、思维导图教学过程一、谈话引入孩子们,你们认识这位老人吗?(课件出示孔子)。
他是孔子,我国春秋末期伟大的思想家教育家,他的思想传承了几千年,今天老师带来了一句,大家一起读一读“学而时习之,不亦悦乎”,是什么意思呢?学过的知识时常拿出来温习,不也是件很愉快的事情吗?今天我们就一起进入第三单元运算定律的整理与复习。
二、归纳整理1.分类我们学习了很多的运算定律和性质,你有好的方法将它们条理清晰地罗列出来吗?思维导图,分类整理。
如何分类?(根据运算种类分为加法运算定律,乘法运算定律,减法的性质,除法的性质四大类)。
2.小组合作请拿出桌上的思维导图,同桌前后四人一组,每人负责一大类,先用文字进行口述,再将定律或性质的名称、字母式填入思维导图相应位置。
3.汇报展示课件出示:每组推选两名代表,随机抽取两条定律或性质,一人负责口述,另一人负责将名称和字母公式贴于思维导图相应位置。
下面的同学认真倾听,有不完善的地方请举手。
(既锻炼了学生的表述能力,也考验了学生的临场发挥能力)4.你觉得哪些定律有些相似,又有些什么不同?(通过对比,便于区分与记忆)加法交换律和乘法交换律相似,只是运算符号不同。
四年级数学上册《整数四则混合运算》整理与复习《四则混合运算》整理与复习【知识点拨】1.四则混合运算的顺序:①在没有括号的算式里,只有加法和减法,或者只有乘法和除法,要从左往右依次计算;既有加减法,又有乘除法,要先算乘除,后算加减。
②在有括号的算式里,要先算括号里面的,再算括号外面的。
改变算式的运算顺序,可以使用小括号。
2.四则混合运算方法一看、(看数字,运算符号,想想运算顺序是什么。
)二画、(画线,哪一步先算,就在哪一步的下面画一条横线,没有计算的要照抄下来。
) 三算、(按照运算顺序计算)四检验、(检验运算顺序是否错误,计算是否算错。
)* 混合运算顺序歌通览全题定方案,细看是否能简便;明确顺序是关键,同级只要依次算;异级出现仔细看,先乘除来后加减;遇到括号别慌张,先小后大依次算;每算一步都检验,又对又快喜心间。
【解题技巧】解答式题技巧(一)“看”。
“看”,就是先看一看题目里有几个什么数。
会有几种运算符号;再看一看运算符号和数据有什么特点,有什么内在联系。
如405×(3076-2980)+2136÷89。
看的结果应是:①有5个数;②有4种运算;③含有小括号;④是一道带有小括号的整数四则混合运算题。
又如3.68×[1÷(2.1-2.09)]+0.6。
看的结果应是①含有5个数;②有4种运算;③含有中括号;④是一道带有中括号的小数四则混合式题。
这是小学数学的计算题的答题技巧之一。
(二)“定”。
“定”,就是对题目整体观察后,确定运算顺序。
即先算什么,再算什么,后算什么。
可采用画线标序的方法,如:405×(3076-2980)+2136÷89└──┬─┘①└─┬─┘└──┬──┘└──────┘③(三)“想”。
“想”,就是分析题中的数值特征和运算间的联系,联想到有关运算定律、运算性质,然后进行运算。
如:405×(3076-2980)+2136÷89。