精品 七年级数学上册 图形认识初步

七年级数学上第四章图形的初步认识单元教学计划第四章：图形认识初步本章介绍了多种图形，包括立体图形和平面图形。

其中，点、线、角等是最基本的图形。

通过自主探究和实例，我们可以探索“两点确定一条直线”和“两点间线段最短”的性质，认识角以及角的表示方法、度量、画法、比较、余角和补角等。

此外，我们还可以探索比较线段长短的方法和线段中点。

这些概念都是认识复杂图形的基础，因此，本章在初中数学中占有重要的地位。

本章涉及到的主要数学思想和方法包括分类讨论思想、方程的思想和由特殊到一般的思想。

分类讨论思想可以解决直线上的点点位置不确定的问题，或者从公共端点出发的一条射线在角内或角外的不确定问题。

方程的思想则可以用于涉及线段和角度的计算中，通过列方程求解，可以清楚简捷地表示出几何图形中的数量关系。

由特殊到一般的思想则主要体现在依靠图形寻找规律的题中。

本章的教学重点包括角的比较与度量、余角和补角的概念和性质，以及直线、射线、线段和角的概念和性质。

教学难点则在于正确表达概念和性质的几何语言，以及建立空间观念。

本章的教学目标包括体验、感受和认识以生活中的事物为原型的几何图形，初步了解从具体事物中抽象出几何概念的方法，以及特殊与一般的辩证关系。

我们还可以画出从不同方向看一些基本几何体以及它们的简单组合得到的平面图形，了解直棱柱、圆柱、圆锥的展开图，能根据展开图想象和制作立体模型。

通过丰富的实例，我们可以进一步认识点、线、面、体，理解它们之间的关系，并在平面图形和立体图形相互转换的过程中，初步建立空间观念，发展几何直觉。

此外，我们还可以逐步掌握学过的几何图形的表示方法，能根据语句画出相应的图形，会用语句描述简单的图形。

四、主要教学方法、手段、选用的教学媒体本章教学采用小组合作、讲授法和练法相结合的教学方法。

在教学过程中，将使用小黑板和班班通等多种教学媒体辅助教学。

五、课时安排本章教学时间约为16课时，具体分配如下：4.1几何图形约4课时，主要介绍基本几何图形的定义、性质及分类。

第四章图形认识初步一、基础知识梳理从不同方向看立体图形立体图形平面图形展开立体图形直线：两点确定一条直线几何图形射线：向一方无线延伸性质：两点之间，线段最短中点：等分线段平面图形线段画法比较角的度量度量法角的大小比较叠合法角角的平分线等角的余角相等余角和补角等角的补角相等二、知识点梳理及考点链接（一）多姿多彩的图形1．立体图形：有些几何图形的各部分不都在同一平面内，他们都是立体图形常见的立体图形有：A柱体：棱柱和圆柱B椎体：棱锥和圆锥C球2．平面图形：有些几何体的各部分都在同一平面内，它们是平面图形。

常用的平面图形有：线段、角、正方形、长方形、三角形、圆等3.从不同方向看物体：正面、上面、左面4.立体图形的展开图5.点、线、面、体几何图形都是由点、线、面、体组成的。

点动成线，线动成面，面动成体。

沙场点兵：1．把下面几何体的标号写在相对应的括号里．长方体：{ } 棱柱体：{ }圆柱体：{ } 球体：{ }圆锥体：{ }2．讲台上放着一本书，书上放着一个粉笔盒，请说明下面的三幅图分别是从哪个方向看到的?①②③3．用如图所示的平面图形可以折成的多面体是______．4．三棱柱有______个顶点，______个面，______条棱，______条侧棱，______个侧面，侧面形状是______形，底面形状是______形．5．笔尖在纸上划过就能写出汉字，这说明了______；汽车的雨刮器摆动就能刮去挡风玻璃上的雨滴，这说明了______；长方形纸片绕它的一边旋转形成了一个圆柱体，这说明了______．二、选择题1．人民英雄纪念碑的中间部分是一个长方体，它的形状类似于()(A)棱柱(B)圆柱(C)圆锥(D)球2．奥运会的标志是五环，这五环中的每一个环的形状与下列哪个形状类似()(A)三角形(B)正方形(C)圆(D)长方形3．下图中，不是左图所示物体视图的是()4．下列四张图中，能经过折叠围成一个棱柱的是()．5．将下面的直角梯形绕直线l旋转一周，可以得到如下图所示的立体图形的是()．6．下列说法错误的是()．(A)长方体、正方体都是棱柱(B)棱柱的侧棱长都相等(C)棱柱的侧面都是三角形(D)如果棱柱的底面各边长相等，那么它的各个侧面的面积一定相等三、解答题1．下图中哪些图形是立体的，哪些是平面的?2．如图所示的几何体是四棱锥，它是由______个三角形和一个形组成的．（二）直线、射线、线段1.直线：直线是最简单、最基本的几何图形之一，是一个不做定义的原始概念，常用“一根拉得很紧的细线”来进行形象描述。

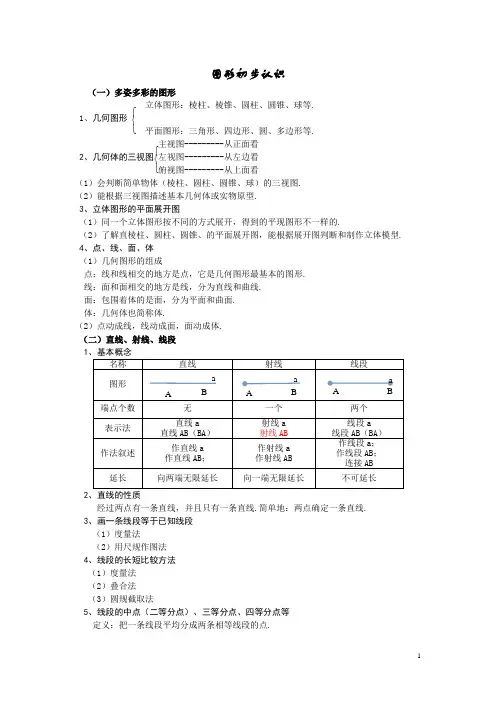
⎧⎨⎩⎧⎨⎩图形初步认识（一）多姿多彩的图形立体图形：棱柱、棱锥、圆柱、圆锥、球等. 1、几何图形 平面图形：三角形、四边形、圆、多边形等.主视图---------从正面看 2、几何体的三视图 左视图---------从左边看俯视图---------从上面看（1）会判断简单物体（棱柱、圆柱、圆锥、球）的三视图. （2）能根据三视图描述基本几何体或实物原型. 3、立体图形的平面展开图（1）同一个立体图形按不同的方式展开，得到的平现图形不一样的.（2）了解直棱柱、圆柱、圆锥、的平面展开图，能根据展开图判断和制作立体模型. 4、点、线、面、体 （1）几何图形的组成点：线和线相交的地方是点，它是几何图形最基本的图形. 线：面和面相交的地方是线，分为直线和曲线. 面：包围着体的是面，分为平面和曲面. 体：几何体也简称体.（2）点动成线，线动成面，面动成体. （二）直线、射线、线段 1、基本概念名称 直线 射线 线段 图形端点个数 无 一个 两个 表示法 直线a直线AB （BA ） 射线a 射线AB 线段a 线段AB （BA ） 作法叙述 作直线a 作直线AB ； 作射线a 作射线AB 作线段a ； 作线段AB ； 连接AB 延长向两端无限延长向一端无限延长不可延长2、直线的性质经过两点有一条直线，并且只有一条直线.简单地：两点确定一条直线. 3、画一条线段等于已知线段 （1）度量法（2）用尺规作图法 4、线段的长短比较方法 （1）度量法 （2）叠合法 （3）圆规截取法5、线段的中点（二等分点）、三等分点、四等分点等 定义：把一条线段平均分成两条相等线段的点.A B a A B a A B a图形：A M B符号：若点M 是线段AB 的中点，则AM=BM=21AB ，AB=2AM=2BM. 6、线段的性质两点的所有连线中，线段最短.简单地：两点之间，线段最短. 7、两点的距离连接两点的线段的长度叫做两点的距离（距离是线段的长度，而不是线段本身）. 8、点与直线的位置关系（1）点在直线上（或者直线经过点） （2）点在直线外（或者直线不经过点）. （三）角1、角：有公共端点的两条射线所组成的图形叫做角.2、角的表示法（四种）：表示方法 图例 记法 适用范围用三个大写字母表示 ∠AOB 或∠BOA任何情况下都适应。

七年级数学“第三章图形认识初步”简介《义务教育课程标准实验教科书·数学》七年级上册第三章是“图形认识初步”。

这一章是义务教育第三学段“空间与图形”领域的起始章，在这一章，将在前面两个学段学习的“空间与图形”内容的基础上，让学生进一步欣赏丰富多彩的图形世界，看到更多的立体图形与平面图形，初步了解立体图形与平面图形之间的关系，并通过线段和角认识一些简单的图形，并能初步进行应用。

本章共安排了4个小节以及两个选学内容，教学时间约需14课时，大体分配如下（仅供参考）：3.1 多姿多彩的图形约4课时实验与探究七桥问题与一笔画3.2 直线、射线、线段约2课时阅读与思考长度的测量3.3 角的度量约3课时3.4 角的比较与运算约3课时数学活动小结约2课时一、教科书内容和课程学习目标本章知识结构如下图所示：本章的主要内容是图形的初步认识，教科书从学生生活周围熟悉的物体入手，使学生对物体的形状的认识从感性逐步上升到抽象的几何图形。

通过从不同方向看立体图形和展开立体图形，初步认识立体图形与平面图形的联系。

在此基础上，认识一些简单的平面图形——直线、射线、线段和角。

人们生活的空间存在着大量的图形，学习有关空间与图形的知识能使人们更好的适应生活的空间。

因此，教科书首先从大量的实例入手，让学生从生活中的物体中抽象出一些常见的几何图形，认识常见的几何图形并进一步认识点、线、面、体，在此基础上，通过从不同方向看立体图形和展开立体图形等活动，在立体图形与平面图形的转换中发展学生的空间观念。

直线、射线、线段和角都是一些最简单的几何图形，比较复杂的图形都是由最简单的图形组成的，有关直线、射线、线段和角的概念和性质也是研究比较复杂的图形如三角形、四边形……“多姿多彩的图形”“直线、射线、线段”“角的度量”“角的比较与运算”的内容，结合丰富的实例，进一步认识角，以及角的表示方法，角的度量，角的画法。

角的比较，补角和余角等内容。

本章的内容是以后学习的重要基础，其中如何结合立体图形与平面图形的互相转化的学习，来发展空间观念以及一些重要的概念、性质等是本章的重点。

初一上册数学知识点：图形初步认识下面是小编为了帮助同学们学习数学知识而整理的初一上册数学知识点：图形初步认识，希望能够帮助到同学们!(一 )多姿多彩的图形立体图形：棱柱、棱锥、圆柱、圆锥、球等.1、几何图形平面图形：三角形、四边形、圆等.主(正)视图 --------- 从正面看2、几何体的三视图侧(左、右)视图-----从左(右)边看俯视图 --------------- 从上面看(1)会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图 .(2)能依照三视图描述基本几何体或实物原型.3、立体图形的平面张开图(1)同一个立体图形按不同样的方式张开，获取的平现图形不一样的 .(2)认识直棱柱、圆柱、圆锥、的平面张开图，能依照张开图判断和制作立体模型.4、点、线、面、体(1)几何图形的组成点：线和线订交的地方是点，它是几何图形最基本的图形.线：面和面订交的地方是线，分为直线和曲线.面：包围着体的是面，分为平面和曲面.体：几何体也简称体.(2)点动成线，线动成面，面动成体.(二 )直线、射线、线段1、基本看法图形直线射线线段端点个数无一个两个表示法直线a直线 AB(BA)射线AB线段a线段 AB(BA)作法表达作直线AB;作直线 a 作射线 AB作线段a;作线段 AB;连接 AB延长表达不能够延长反向延长射线AB 延长线段AB;反向延长线段BA2、直线的性质经过两点有一条直线，并且只有一条直线.简单地：两点确定一条直线.3、画一条线段等于已知线段(1)胸襟法(2)用尺规作图法4、线段的大小比较方法(2)叠合法5、线段的中点 (二均分点 )、三均分点、四均分点等定义：把一条线段平均分成两条相等线段的点.图形：A M B符号：若点M 是线段 AB 的中点，则AM=BM=AB，AB=2AM=2BM.6、线段的性质两点的所有连线中，线段最短.简单地：两点之间，线段最短.7、两点的距离连接两点的线段长度叫做两点的距离.8、点与直线的地址关系(1)点在直线上(2)点在直线外 .(三 )角1、角：由公共端点的两条射线所组成的图形叫做角.2、角的表示法 (四种 )：3、角的胸襟单位及换算4、角的分类锐角直角钝角平角周角范围090=90 90 =180=3605、角的比较方法(2)叠合法6、角的和、差、倍、分及其近似值7、画一个角等于已知角(1)借助三角尺能画出15 的倍数的角，在 0～ 180 之间共能画出 11 个角.(2)借助量角器能画出给定度数的角.(3)用尺规作图法 .8、角的平线线定义：从一个角的极点出发，把这个角分成相等的两个角的射线叫做角的均分线.图形：符号：9、互余、互补(1)若 2=90，则 1 与 2 互为余角 .其中 1 是 2 的余角， 2 是 1的余角 .(2)若 2=180，则 1 与 2 互为补角 .其中 1 是 2 的补角， 2 是 1的补角 .(3)余 (补)角的性质：等角的补(余 ) 角相等 .课本、报刊杂志中的成语、名言警句等俯首皆是,但学生写作文运用到文章中的甚少,即使运用也很难做到恰到利处。