群论的各种应用复习过程
- 格式:doc
- 大小:95.50 KB
- 文档页数:2


群论的基本理论及其应用群论是现代数学中的一个重要分支,它研究的对象和思想对现代科学和技术的发展具有深远影响。
本文将简要介绍群论的基本理论,包括群的定义和基本性质、同构与同态、正则表示等,以及群论在物理、化学、密码学等领域的应用。
一、群的定义和基本性质群是指一个集合G,和一个二元运算“·”,满足以下四个条件:1. 封闭性:对于任意的a,b∈G,a·b∈G。
2. 结合律:对于任意的a,b,c∈G,(a·b)·c=a·(b·c)。
3. 单位元:存在一个元素e∈G,对于任意的a∈G,有a·e=e·a=a。
4. 逆元:对于任意的a∈G,存在一个元素a^-1∈G,使得a·a^-1=a^-1·a=e。
以上四个条件被称作群的基本公理,满足这些公理的集合和运算就构成了一个群。
除了以上四个基本性质,群还具有一些重要的衍生性质,如:1. 唯一性:群的单位元和逆元是唯一的。
2. 闭合性:群的任意子集在运算下仍构成一个群。
3. 基本定理:任意群都同构于一个置换群。
二、同构与同态同构和同态是群论中最重要的概念之一。
同构指两个群之间存在一个双射函数,满足这个函数保持乘法运算,即对于任意的群元素a,b∈G,有f(a·b)=f(a)·f(b)。
同构很像一种数学上的等价关系,它说明两个群结构上是相同的。
同态指两个群之间存在一个映射,满足这个映射保持群的乘法和单位元素,即对于任意的群元素a,b∈G,有f(a·b)=f(a)·f(b)且f(e)=e',其中e和e'分别是两个群的单位元素。
同态具有保持群结构的性质,它将一个群映射到另一个群上,并保留了群的结构特征。
三、正则表示群的正则表示是指把一个任意群转化成可逆矩阵群的一种数学方法。
这种转化方法常用于群论与物理学、化学等学科的交叉研究领域。
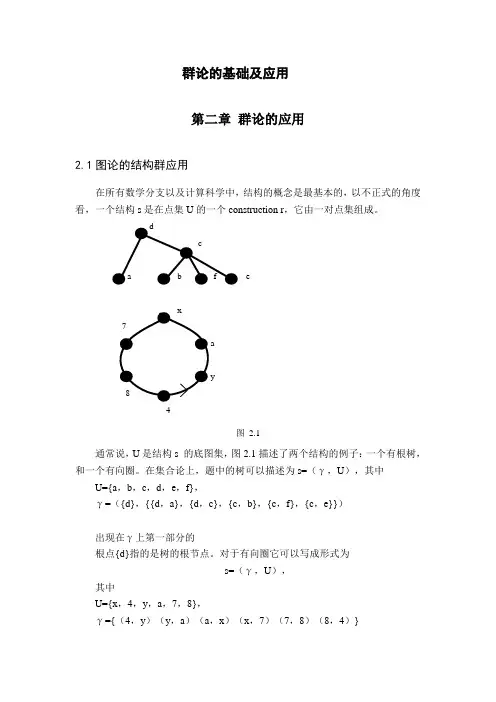
群论的基础及应用第二章群论的应用2.1图论的结构群应用在所有数学分支以及计算科学中,结构的概念是最基本的,以不正式的角度看,一个结构s是在点集U的一个construction r,它由一对点集组成。
e4图 2.1通常说,U是结构s 的底图集,图2.1描述了两个结构的例子:一个有根树,和一个有向圈。
在集合论上,题中的树可以描述为s=(γ,U),其中U={a,b,c,d,e,f},γ=({d},{{d,a},{d,c},{c,b},{c,f},{c,e}})出现在γ上第一部分的根点{d}指的是树的根节点。
对于有向圈它可以写成形式为s=(γ,U),其中U={x,4,y,a,7,8},γ={(4,y)(y,a)(a,x)(x,7)(7,8)(8,4)}U={a ,b ,c ,d ,e ,f}σV={x ,3,u ,v ,5,4}图2.2考虑有根树s=(γ,U )它的底图集是U ,通过图2.2中的σ变换,将U 中每一个元素替换成V 中的元素,这幅图清晰的显示了变换中如何将结构树s 对应到集合V 上相应的树t=(τ,V ),我们说树t 可以由树s 通过变换σ得到。
记作t=σ·s.则树s 和树t 是同构的,σ叫做s 到t 的同构。
我们可以将底图的点视为无标记的点,这样就得到同构图的通用形式。
如果σ是U 到U ,则它是自同构。
此时树的变换σ·S 等价于树s ,即s=σ·s.我们已经知道结构s 的定义,那么可以定义它在规则F 下的结构群,我们用F[U]表示集合U 上所有满足F 的结构F[U]={f|f=(γ,U ),γ⊆ϑ[U]}其中ϑ[U]表示U 中所有未排序的元素对所组成的边。
一个结构群满足规则F :1.对任意一个有限集U ,都存在一个有限集F[U]2.对每一个变换σ:U →V ,存在一个作用 F[σ]:F[U]到F[V] 进一步F[σ]满足下列函数性质: 1.对所有的变换σ:U →V 和τ :V →W F[σ·τ]=F[τ]·F[σ];2.对恒等映射一个元素s 数域F[U]叫做U 上的一个F 结构,作用F[σ]称为F 结构在σ下的变换。

第二章群论复习题答案第二章群论复习题答案在群论中,群是一种代数结构,它由一组元素和一种二元运算组成。
群论是现代数学中的一个重要分支,它研究的是群的性质和结构。
在本文中,我们将回顾第二章的群论复习题,并给出相应的答案。
1. 证明:如果G是一个群,那么单位元是唯一的。
证明:假设G是一个群,e和e'都是G的单位元。
根据群的定义,对于任意的g∈G,有g·e=g和g·e'=g。
我们可以将e'代入第一个等式中,得到g·e'=g·e。
由于群的乘法满足结合律,我们可以将等式右边的e'和e交换位置,得到g·e=e'·g。
再次使用单位元的定义,我们得到g=e'·g。
由于g是任意的元素,所以对于任意的g∈G,都有g=e'·g成立。
根据群的封闭性,我们可以将g取为e,得到e=e'·e=e'。
因此,我们证明了单位元是唯一的。
2. 证明:如果G是一个群,那么每个元素都有唯一的逆元。
证明:假设G是一个群,对于任意的g∈G,我们需要证明存在唯一的g'∈G,使得g·g'=e。
首先,我们证明存在性。
由于G是一个群,对于任意的g∈G,存在一个元素g''∈G,使得g·g''=e。
我们可以将g''记作g',则有g·g'=e。
其次,我们证明唯一性。
假设存在另一个元素h∈G,使得g·h=e。
我们可以将等式两边左乘g',得到(g·g')·h=g'·e=g'。
由于群的结合律成立,我们可以将等式左边的括号去掉,得到g·(g'·h)=g'。
由于g'是g的逆元,所以g'·g=e。

第二章群论复习题答案第二章群论复习题答案群论是数学中的一个重要分支,研究的是群的性质和结构。
在群论的学习过程中,复习题是非常重要的一部分,通过解答复习题可以加深对群论的理解和应用。
本文将给出第二章群论复习题的答案,并对其中涉及的概念和定理进行解释和讨论。
1. 设G是一个群,证明单位元是唯一的。
解答:假设G中有两个单位元e和e',则有e * e' = e' * e = e,其中*表示群的运算。
由于e是单位元,所以e * e' = e' * e = e'。
再由e'是单位元,可得e * e' = e'。
结合上述两个等式,可以得到e = e'。
因此,单位元是唯一的。
2. 设G是一个群,证明每个元素都有唯一的逆元。
解答:假设G中的元素a有两个逆元a'和a'',则有a * a' = a' * a = e和a * a'' = a'' * a = e,其中e表示单位元。
由于a'是a的逆元,所以a * a' = e。
再由a''是a的逆元,可得a * a'' = e。
结合上述两个等式,可以得到a' = a''。
因此,每个元素都有唯一的逆元。
3. 设G是一个群,证明对于任意的元素a和b,有(a * b)^-1 = b^-1 * a^-1。
解答:根据群的性质,对于任意的元素a和b,(a * b)^-1是(a * b)的逆元。
即(a * b) * (a * b)^-1 = (a * b)^-1 * (a * b) = e,其中e表示单位元。
将等式左边展开,得到a * b * (a * b)^-1 = e。
再将等式右边展开,得到(a * b)^-1 * a * b = e。
由于群的结合律,可以将等式左边重新排列为a * (b * (a * b)^-1) = e。

高等代数中的群论基本概念与运算规律在高等代数中,群论是一个重要的数学分支,它研究的是集合与运算之间的关系。
群论的基本概念和运算规律对于理解和应用代数学知识具有重要意义。
本文将介绍群论的基本概念和运算规律,以帮助读者更好地理解这一领域的内容。
一、群的定义与性质群是代数结构的一种形式,它由一个集合G和一个二元运算*组成。
如果满足以下条件,那么G就是一个群:1. 封闭性:对于任意的a、b∈G, a * b也属于G。
2. 结合律:对于任意的a、b、c∈G,(a * b) * c = a * (b * c)。
3. 单位元:存在一个元素e∈G,使得对于任意的a∈G,a * e = e *a = a。
4. 逆元:对于任意的a∈G,存在一个元素b∈G,使得a * b = b * a = e。
以上四个条件是群的基本性质,可以看出群中的运算是封闭的、结合的,并且存在单位元和逆元。
二、群的例子1. 整数集:整数集(Z,+)构成一个群,其中+表示整数的加法运算。
单位元为0,任意整数a的逆元为-a。
2. 实数集:实数集(R,+)构成一个群,其中+表示实数的加法运算。
单位元为0,任意实数a的逆元为-a。
3. 矩阵集合:矩阵集合(M,*)构成一个群,其中*表示矩阵的乘法运算。
单位元为单位矩阵,任意可逆矩阵A的逆元为A的逆矩阵。
三、群的运算规律1. 结合律:群的运算满足结合律,即对于任意的a、b、c∈G,(a *b) * c = a * (b * c)。
2. 唯一性:群的单位元是唯一的,即不存在两个不同的单位元。
3. 逆元唯一性:群的每个元素都有唯一的逆元,即不存在两个不同的逆元。
4. 交换律:如果群的运算满足交换律,即对于任意的a、b∈G,a *b = b * a,则称该群为交换群或可交换群。
以上运算规律是群论中的基本性质,对于研究和解决问题具有很大的帮助。
四、子群和同态在群论中,子群和同态是两个重要的概念。
1. 子群:如果一个群H是另一个群G的子集,并且H中的元素在G的运算下仍然构成一个群,那么H就是G的子群。

群论讲课提纲第一章 抽象群理论1.1 群的基本概念1、群的定义 实例分析; 群的定义。
2、基本概念有限群与无限群(群的阶); 连续群与分立群; 阿贝群(交换群),例题;对称群,例题(234444{,,,,,,,}x y C E C C C m m νμνσσ=);循环群(生成元)1.2 有限群的基本性质 1、群的乘法表(群乘表) 群乘表构造方法(SL2群,4C ν群) 群乘表的性质(重排定理及推论) 2、元素的阶 例题分析定义(元素的阶)几点结论 3、元素的共轭 定义(共轭元素)共轭的性质(自反、对称、传递) 4、共轭类等价关系与集合的划分 共轭类的定义关于类的几个结论(7条,例题)类的积(i j ijk k kC C a C =∑,例题)1.3 子群与商群1、子群的概念 定义、判别条件、平凡子群2、陪集(旁系) 定义 例题与分析 陪集的性质① 子群与它的任何一个陪集没有共同元素, 即&,X G X H XH H HX H Φ∀∈∉⋂=⋂=② 子群的任何两个左(右)陪集要么完全相同,要么完全不同。
即,:XH YH or XH YH Φ=⋂=③ 子群与它的所有相异左(右)陪集定义群的一个划分*。
推论1:群的阶与子群的阶之比为整数,即G nk Hm==;推论2:群阶与元素阶的商为整数。
3、共轭子群定理:以群G 中任何元素为过渡元素对子群1H 作共轭变换得到的集合2H 仍然是G 的子群,称为1H 的共轭子群。
例题4、正规子群(自轭子群、不变子群)例题分析正规子群的两种定义 正规子群的性质 ① 不变子群的任何两个陪集的积仍然是该子群的陪集;② 不变子群与其任何一个陪集的积等于该陪集。
5、商群例题分析定理:由正规子群及其所有相异陪集构成群称为商群。
商群的性质 ① 商群/G H 的幺元是正规子群H ;② 商群的阶数为正规子群的指数/n m ;1.4 群的同构与同态 1、 群的同构 ① 例题分析 ② 同构的定义 ③ 注意事项④ 4C 群所有子群的同构关系2、 群的同态① 例题分析 ② 同态的定义③ 注意事项3、有限群的结构① 1~6阶群的结构分析(思考题) ② 关于高阶群结构分析的注意事项 群的生成集存在性素数阶群的结构③ 生成集定理1.5 置换群① 置换群的基本概念 ② 3S 群及其乘法表 ③ n S 群的性质④ 任何有限群总同构于n S 群的一个子群。


群论第⼆章考前复习总结第⼆章考前复习总结1.1节群1.对称变换:保持系统不变的变换。
(背)群,,所有对称变换只有6个:2. 群是⼀个集合,其中定义了元素的“乘积”法则,这个集合G满⾜4个条件:封闭性、结合律、存在恒元、逆元,这个集合就称为群。
(背)任何两个元素相乘还在这个集合中(背)任意元素乘恒元等于这个元素(背)元素乘逆元等于恒元。
(背)U(n)群:全体n维⼳正矩阵的集合。
⼳正:O(n)群:全体n维实正交矩阵的集合。
正交:,实正交:矩阵元是实数6)乘积的逆:9)有限群的阶:有限群中的元素数⽬4.循环群及其⽣成元1)循环群:由⼀个元素 Rn:循环群的阶,即有限群的元素个数。
R:循环群的⽣成元循环群的阶和其⽣成元的阶相等。
⽣成元的阶是满⾜的最⼩正整数n。
循环群都是阿贝尔群(阿贝尔群不⼀定是循环群)。
R⽣成的群是⼀个nn R是系统的对称变换,则轴称为n次固有转动轴(n次轴),此时转动R称为n次转动轴的⽅向:转动R由右⼿螺旋法则得到,⼤拇指指向轴的正⽅向。
1)元素R 的周期:由有限群的任⼀元素 R 及其幂次⽣成的集合。
2)有限群的⽣成元:有限群的群元素可以由最⼩数⽬个群元素的乘积⽣成3)有限群的秩:⽣成元的个数4)有限群⽣成元的选择并不唯⼀,但秩不变。
在验证B=DA 这种关系时,正三⾓形的三个字母必须画成:这种情况。
6.有限群的重排定理1)复元素:把有限群部分元素的集合2)群的重排定理(考试简答题)设T 是群G = {E, R, S, …}中任⼀确定元素,则下⾯三个集合与原群G 相同 (背)复元素的逆是每个元素取逆7.同构元素是对应的,在这种对应规则下,元素的乘积也是对应的。
群G3)循环群的乘法表4)四阶群(即有4群群:⼀个恒元加3个2阶元素。
其为:5a.含零个三阶元素,即群只含⼀个恒元加5个⼆阶元素。
这种情况不成⽴。
称),⼆阶、三阶、四阶、五阶的群都是阿贝尔群。
6)正N 边形对称变换群1个N 次轴,N 个⼆次轴。

群论在数学中的应用群论是一门研究对称性的数学分支,它在现代数学以及物理学、化学和计算机科学等领域中都有着广泛的应用。
本文将从基础概念开始,介绍群论在数学中的应用。
1. 群的基本概念群是一种数学结构,它由一个集合和一个二元运算组成,且满足以下四个条件:1) 封闭性:对于任意两个元素,它们的运算结果仍然属于群中;2) 结合律:群中元素的运算满足结合律;3) 存在单位元素:群中存在一个元素,称作单位元素,使得任意元素和单位元素的运算结果仍然是该元素本身;4) 存在逆元素:群中任意元素都有一个逆元素,满足它们的运算结果为单位元素。
群中的二元运算可以是加法、乘法、函数的复合等,而集合中的元素可以是实数、复数、矩阵、置换等。
2. 群在数学中的应用1) 置换群在离散数学中,置换是一种重要的对象。
置换就是一种将集合元素重新排列的方式,可以用一个有限大小的环图表示。
例如,置换(1 2 3)(4 5)表示将1,2,3三个元素互相排列,4,5两个元素互相排列,且不改变它们之间的相对位置。
置换群就是由所有置换组成的群,它的运算是置换的复合,即把两个置换合并成一个。
置换群在数学中的应用非常广泛,可以用于研究数学中的对称性和群论中的概念。
2) 群理论在密码学中的应用在密码学中,群论被广泛应用于公钥密码学算法中。
公钥密码学采用了数学中的离散对数问题,利用群论中的阶和循环群等概念,构造了一些安全性高的加密算法。
其中最著名的是RSA算法,它利用了群论中质数分解的困难性。
3) 群论在实分析中的应用实分析是数学中研究实数、实函数和实变量的一门学科。
在实分析中,群论被用来研究实数和实函数的对称性。
例如,可以将函数看作群中的元素,函数的可加性就等价于群中元素的结合律,而函数的复合就等价于群中的运算。
通过研究群论的性质,可以发现函数的对称性和它们的性质之间的关系,进而得到更多有用的结果。
4) 群论在量子力学中的应用量子力学是物理学中的一门分支,它研究微观粒子的性质和相互作用规律。
群论总结笔记什么是群论群论(Group Theory)是数学中的一个分支领域,主要研究代数结构中的一类称为群的对象及其性质、结构和应用。
群论在代数学中具有重要的地位,被广泛应用于数学、物理学、化学等领域。
本文将总结群论的基本概念、性质以及一些常见的应用。
群的定义与性质在群论中,群是指一个非空集合G以及在G上定义的一个二元运算*,满足以下四个条件:1.封闭性:对于任意的a、b∈G,其运算结果a*b仍然属于集合G;2.结合律:对于任意的a、b、c∈G,满足(a b)c = a(b c);3.单位元存在性:存在一个元素e∈G,使得对于任意的a∈G,有a e=e a=a;4.逆元存在性:对于任意的a∈G,存在一个元素b∈G,使得a b=b a=e。
其中,运算*通常表示为乘法,单位元表示为1,逆元表示为a的倒数a-1。
群论中的一些常见性质包括:•结合律:对于群G中的任意三个元素a、b、c,满足(a b)c = a(b c);•存在唯一的单位元:群中的单位元是唯一的,记作e;•存在唯一的逆元:群G中的任意元素a都存在唯一的逆元a-1;•可交换性:如果对于群G中的任意两个元素a、b,都满足a b=b a,则称该群为交换群或阿贝尔群。
群的例子群的概念可以从许多不同的角度来理解。
下面列举了几个常见的群的例子:1.整数加法群:以整数集合Z为基础,定义二元运算为加法。
群单位元为0,逆元为负数。
2.整数乘法群:以非零整数集合Z*(不包括0)为基础,定义二元运算为乘法。
群单位元为1,逆元为倒数。
3.对称群:对称群是一个由所有n个元素的置换组成的群。
其中n称为置换数,对称群记作Sn。
4.旋转群:平面上所有围绕一个固定点旋转的变换构成的群。
旋转群可表示为SO(2),其中O(2)代表二维正交矩阵的集合。
这些仅是群论研究的众多例子中的几个,群可以从不同的领域中产生,如代数、几何、拓扑等。
群的应用群论在数学和其他学科中具有广泛的应用。
第二章群论复习题群论是数学中的一个重要分支,它研究的是集合上的代数结构,特别是满足特定条件的集合和其上的运算。
以下是对群论的一些基本复习题,以帮助学生巩固和复习相关知识。
1. 群的定义:给出群的四个基本条件,并举例说明哪些集合和运算可以构成群。
2. 子群:解释什么是子群,并给出一个群的子群的例子。
3. 群的运算:说明群的运算必须满足封闭性、结合律、单位元存在以及每个元素都有逆元。
4. 群的同态和同构:定义群的同态和同构,并给出一个群同态的例子。
5. 循环群:解释什么是循环群,并给出一个循环群的例子。
6. 阿贝尔群:定义阿贝尔群,并说明所有循环群都是阿贝尔群。
7. 群的阶:解释群的阶是什么,并给出如何计算一个群的阶。
8. 拉格朗日定理:陈述拉格朗日定理,并解释它在群论中的重要性。
9. 正规子群和商群:定义正规子群和商群,并给出一个例子说明如何构造一个群的商群。
10. 群的表示:简要介绍群的表示是什么,以及它在数学和物理学中的应用。
11. 群的直积和自由群:解释群的直积和自由群的概念,并给出一个群的直积的例子。
12. 群的简单性:定义什么是群的简单性,并给出一个简单群的例子。
13. 群的分类问题:简要介绍有限群的分类问题,并说明为什么这是一个重要的数学问题。
14. 置换群:解释置换群的概念,并说明它在群论中的作用。
15. 群的生成集:定义群的生成集,并给出一个群的生成集的例子。
这些问题覆盖了群论的基本概念和理论,通过解答这些问题,学生可以加深对群论的理解,并为进一步的学习和研究打下坚实的基础。
希望这些复习题能够帮助学生更好地掌握群论的知识。
群论基础知识讲解
嘿,朋友!咱们今天来聊聊群论这个神秘又有趣的东西。
你知道吗?群论就像是一个魔法盒子,里面装满了各种奇妙的规则
和秘密。
先来说说啥是群。
想象一下,你有一群小伙伴,大家在一起玩游戏,有着特定的玩法和规则,这就有点像群啦!比如说,你们规定只能向
前走三步或者向后退两步,这就是一种规则。
群里有个重要的概念叫“封闭性”。
这就好比你在一个封闭的房间里,不管怎么折腾,都还在这个房间里。
在群里,不管你怎么对元素进行
操作,得到的结果还是在这个群里。
还有“结合律”,这就好像是搭积木,不管先把哪几块积木拼在一起,最后的结果都不会变。
再说说“单位元”,它就像是一个魔法原点,任何元素和它结合,都
不会改变自身。
比如说数字运算中的 0 ,任何数加 0 都还是原来那个数。
“逆元”也很有意思,它就像是每个元素的“克星”。
比如数字 5 ,它
的逆元就是 -5 ,两者相加就等于那个神奇的单位元 0 。
群论在生活中的应用可不少呢!比如说密码学,那些复杂的加密算
法背后,群论可出了不少力。
就好像给你的秘密穿上了一层厚厚的铠甲,让别人很难破解。
再想想,我们的钟表,从 1 点走到 12 点又回到 1 点,这是不是也
有点群的意思?
学习群论就像是在探索一个神秘的宝藏,一开始可能会觉得有点迷糊,但只要你坚持,慢慢就能发现其中的乐趣和奥秘。
朋友,你想想,如果没有群论,我们的世界得少多少精彩啊!所以,好好去感受群论的魅力吧,说不定你能在这个神奇的世界里发现更多
让人惊叹的东西!。
物理学中的群论及其应用物理学是自然科学中最具基础性和深刻性的科学之一,与其他学科相比,它具有其独特的数学基础。
在物理学中,群论是一种强大的工具,被广泛应用于描述和解决物理现象。
一、群论的基础知识群是一种数学结构,它描述了一组对象在某种形式下的对称性质。
在群论中,对称性是一个核心概念。
对于一个集合G,如果它满足以下几个性质:闭合性、结合律、存在单位元素和逆元素,则称为群。
群论的基础是群的代数和几何性质,其中最基本的是群的阶和群的子群。
群的阶指的是群中元素的个数,它是群的基本类别。
而群的子群是指群中的一些元素形成的子集合成的群,它是群的一个重要概念。
群的子群可以帮助我们理解它的对称性质。
二、群论的应用1、晶体学在晶体学中,群论是非常重要的。
晶体是指一个重复的具有长程序的固体结构,晶体的对称性质可以用群论来描述。
对于晶体物理学家来说,群论是一种有效的工具,可以帮助他们推导出新的晶体结构,并且预测物理特性,如折射率和电导率等。
2、量子力学在量子力学中,群论被用来描述美那空间中的对称性质。
对于一个物理系统,如果它在某个对称操作下不变,则称为该物理系统具有对称性。
例如,对于一个在三维空间中的量子态,我们可以用SU(3)群描述其对称性质。
3、场论场论是研究物质中的场和它们之间相互作用的物理学分支。
场论中群论被用于描述场的对称性质。
在场的变换下,场的表现形式会发生改变,但是物理定律保持不变。
这种对称性被称为规范对称性,它是一种非常重要的群论应用。
4、粒子物理学在粒子物理学中,群论是必不可少的。
粒子物理学家研究基本粒子的性质和相互作用,这涉及到对称性和群论的应用。
在标准模型理论中,SU(3)×SU(2)×U(1)群被用来描述基本粒子的相互作用。
三、结论群论在物理学中具有重要的地位,它不仅是物理学的理论基础之一,也是物理学家解决问题的重要工具之一。
群论依赖于代数和几何性质,可以帮助我们理解物理系统中的对称性质。
群论的应用
关于几何体或其他数学、物理对象的对称概念看起来很明显,但给对称这个概念一个精确的和一般的描述,特别是对称性质的量上的计算,使用一般的数学工具很困难。
为了研究象对称这样的规律,在18世纪末、19世纪初出现了群论。
群论最初主要研究置换问题,随着群论研究的深入。
群论已成为近世数学的一个重要分支,并分裂成许多或多或少的独立科目:群的一般理论、有限群论、连续群论、离散群论、群的表示论、拓扑群等。
19世纪到20世纪,群通过其表示论在自然科学中得到了广泛的应用,例如在几何学、结晶学、原子物理学、结构化学等领域,群的表示经常出现在具有对称性的问题研究中。
如今,群论的方法和概念,不仅是解决对称规律的重要工具,而且是解决其他许多问题的重要工具。
本文主要是简单说明一下群论在机器人、密码学、网络、原子物理中的应用。
1. 群论在机器人中的应用。
在机器人领域,群论最初主要应用在机器人运动学的研究中,随着研究的进一步深入,机器人的装配,标定和控制等都用到群论。
从群论的角度来看,机器人的位置无论是用矢量表示,还是用旋量表示,或以四元数、双四元数等其他形式表示,其运动变换可以看作是群运算。
因为在变换过程中,连杆的内部结构不变,其变换可以看作是欧几里德群的子群,群中的变换包括旋转和平移两种。
在机器人运动学中,若采用群描述机器人的运动、可以使表达更简洁更通用,便于符号推理,利用群论描述机器人运动还便于设计通用的机器人语言。
在机器人操作中,操作物体通常是对称的或具有对称的特性,用一般的数学工具很难描述其相对位置,而用群可以很方便地描述其相对关系。
特别是在装配任务中,当相互匹配的两个零件具有对称性时,它们有很多装配位置,用一般的数学工具比较难描述,用群就可很容易地表示并进行推理。
机器人在许多操作过程中具有非线性和非完整性,常用的线性控制不能满足其控制性能要求,人们开始用非线性系统的几何理论来解决,其状态变换是在流形上进行的,它使用的工具是李群和李代数,李群是连续群中重要的一种。
2.群论在密码学的应用。
自从1984年N.R.Wager和M.R.Magyarik提出了第一个用组合群论的理论构造公钥密码体制的方法以来,在密码学家们的共同努力下,利用组合群论的理论已经提出多个公钥密码体制和密钥交换协议。
由于组合群论中的数学工具和以前数论中的内容截然不同,有必要对组合群论中的一些定义和定理加以说明,从而可运用到密码学中去,得到不同的加密算法。
群G称作是有限生成的,如果G存在有限个生成元
1,2,
g g…,
n
g,满足G中任意一个元素都可以表示成生成元和它们的逆的有限乘积。
群G 称作是可以有限表示的,如果在G 中有有限个元素1r ,2r ,…,k r 满足在群G 中,1r e =,2r e =,…,k r e =,其中e 是单位元,那么1r ,2r ,…,k r 称为G 的生成元12,,g g …,n g 的一组定义关系,。
换一种角度,如果把群G 看成是n 个元素X ={12,,a a …,n a }生成的自由群F(X)的商群,即存在F(X)的正规子群N ,使得F(X)G=N 成立,那么G 是可以有限表示的意思是:如果1r ,2r ,…k r 对应F(X)中的元素1w ,2w …k w ,那么{12,,w w …},k w 是F(X)的正规子群N 的生成元。
可以有限表示的群G 可表示为:G=21,,g g …,n g ;12,,r r …,k r
3.群论在网络中应用
群论在网络理论中主要用于研究网络理论中的双口网络集合,双口变换器集合, 2n 端口变换器集合,用群论的方法找出了它们之间的联系,为网络的设计和分析简化,寻找出有效的途径,同时也是群论的应用的一个新的领域。
网络理论中的基本双口网络,双口变换器和器件、2n 端口变换和器件,表明网络理论中较为分离的变换器和器件在群论的约束下成为相互依赖的变换器与器件,为网络理论器件的设计提供了理论根据。
4.群论在原子材料中的应用
人类对于组成物质世界的基本“单元”的认识是逐步深入的,1869年门捷列夫排出元素周期表。
是首次从原子层次认识物质世界基本“单元”的规律。
到20世纪,先后发现一千多种原子核。
虽其性质各异、但是人们指示出所有原子核均由二种粒子—中子和质子在核内不同的运动与填充可得。
从而建立了原子核的壳层摸型理论、它成功地解释了核物理现象。
这就是人们常说的第二张周期表,它是从原子核层次来沙识所谓“基本单元”的。
基于二次成功的戈现、得到共同经验:微观世界的人识是无窃尽的;微观世界是有严格规律的。
每引入一种深入层次的拉子,意味着向物质本质迈进一步。
当今,面对庞大的基本粒子家族。
有理由议为它们不是杂乱无章的。
那么组成这些基本粒子大厦的“砖块”又是什么呢?它们按何种规律结合的呢?人们好象又遇到了第三张周期表。
“群论”这个工具扮演了重要角色。
大量核物理实验抬出,基本粒子中的介子、强子等家强中具有su(3)群对称性。
根据su(3)理论,令组成基本粒子的“单元”称为“夸克”。
夸克模型成功地解释了大量实验现象。
正确口也预言了六十年代后期发现的Ω粒子。
令人信服之处还在于“夸克”所允许组合得到的粒子,在实验中均能找到,反之亦然。
总之,群论在社会生活和科学技术中都有很多应用。