常用的Fortran函数

fortran ln函数一、引言Fortran是一种高级编程语言，它最初是为科学和工程计算而设计的。

Fortran有很多内置的数学函数，其中包括ln函数。

在本文中，我们将介绍Fortran中的ln函数以及如何使用它。

二、什么是ln函数ln函数是自然对数函数，它是以e为底数的对数函数。

ln(x)表示e的多少次方等于x，其中e是一个常数(约等于2.71828)，x是一个正实数。

三、Fortran中的ln函数在Fortran中，可以使用log()或log10()来计算对数。

log()计算以e 为底数的对数，而log10()计算以10为底数的对数。

因此，在Fortran中，可以使用以下代码来计算ln(x)：result = log(x)四、示例代码下面是一个简单的示例程序，演示如何在Fortran中使用ln函数：program ln_exampleimplicit nonereal :: x, resultwrite(*,*) 'Enter a positive number: 'read(*,*) xresult = log(x)write(*,*) 'The natural logarithm of ', x, ' is ', resultend program ln_example五、解释在这个程序中，我们首先声明了两个变量：x和result。

x用于存储用户输入的值，result用于存储计算结果。

接下来，我们要求用户输入一个正实数，并将其存储在变量x中。

然后，我们使用log()函数计算ln(x)，并将结果存储在变量result中。

最后，我们将结果输出到屏幕上。

六、结论在本文中，我们介绍了Fortran中的ln函数以及如何使用它。

ln函数是自然对数函数，它是以e为底数的对数函数。

在Fortran中，可以使用log()或log10()来计算对数。

通过一个简单的示例程序，我们演示了如何在Fortran中使用ln函数。

fortran余数函数Fortran是一种编程语言，用于科学计算和数值分析。

它是一种古老而强大的语言，最早于1957年发布。

尽管它已经存在了很长一段时间，但它仍然被广泛使用，特别是在科学和工程领域。

Fortran有许多内置函数，其中一个就是计算余数的函数。

余数函数可以计算两个数相除后的余数。

Fortran中的余数函数称为MOD函数，它可以用来计算整数和实数的余数。

MOD函数有两个参数，一个是除数，另一个是被除数。

当两个参数都是整数时，MOD函数返回一个整数余数。

例如，如果我们要计算13除以5的余数，可以使用以下Fortran代码：```fortranprogram mod_exampleimplicit noneinteger :: dividend, divisor, remainderdividend = 13divisor = 5remainder = MOD(dividend, divisor)write(*,*) "余数为:", remainderend program mod_example```上述代码将输出"余数为: 3"，因为13除以5得到的余数是3。

这个例子中，dividend被赋值为13，divisor被赋值为5，而remainder 则是MOD函数的结果。

除了整数之外，MOD函数还可以用于计算实数的余数。

当被除数和除数都是实数时，MOD函数将返回一个实数余数。

例如，如果我们要计算5.7除以2.1的余数，可以使用以下Fortran代码：```fortranprogram mod_exampleimplicit nonereal :: dividend, divisor, remainderdividend = 5.7divisor = 2.1remainder = MOD(dividend, divisor)write(*,*) "余数为:", remainderend program mod_example```上述代码将输出"余数为: 1.5"，因为5.7除以2.1得到的余数是1.5。

FORTRAN 90标准函数（一）(2012-07-03 17:14:57)转载▼分类：学习标签：fortran函数教育符号约定：●I代表整型;R代表实型;C代表复型;CH代表字符型;S代表字符串;L代表逻辑型;A代表数组;P代表指针;T代表派生类型;AT为任意类型。

●s:P表示s类型为P类型(任意kind值)。

s:P(k)表示s类型为P类型(kind值=k)。

●[…]表示可选参数。

●*表示常用函数。

注：三角函数名前有C、D的函数为复数、双精度型函数。

注：指数函数名、平方根函数名、对数函数名前有C、D的函数为复数、双精度型函数。

表4 参数查询函数atan2函数的值域是多少？我从网上找到一个fortran函数的日志，说此值域是-π~π，但正常反正切函数的值域应该是-π/2~π/2。

对atan2函数不够了解，所以不知道你的答案对不对，我个人认为不对。

我是用正常的反正切函数atan(v/u)来算的：FORTRAN：if (u>0..and.v>0.) dir=270-atan(v/u)*180/piif (u<0..and.v>0.) dir=90-atan(v/u)*180/piif (u<0..and.v<0.) dir=90-atan(v/u)*180/piif (u>0..and.v<0.) dir=270-atan(v/u)*180/piif (u==0..and.v>0.) dir=180if (u==0..and.v<0.) dir=0if (u>0..and.v==0.) dir=270if (u<0..and.v==0.) dir=90if (u==0..and.v==0.) dir=999其中uv等于零的五种情况要单独挑出来，不然程序会有瑕疵。

atan函数换成atand函数的话直接是度数，不用*180/pi我四个象限和轴都试了，应该没错。

1、RANDOM_NUMBERSyntax ['sintæks] n. 语法CALL RANDOM_NUMBER (harvest结果)Intrinsic Subroutine（固有子程序）：Returns a pseudorandom number greater than or equal to zero and less than one from the uniform distribution.返回大于或等于0且小于1，服从均匀分布的随机数2、RNNOA/ DRNNOA （Single/Double precision）Generate pseudorandom numbers from a standard normal distribution using an acceptance/rejection method.产生服从标准正态分布的随机数Usage（用法）CALL RNNOA (NR, R)Arguments（参数）NR— Number of random numbers to generate. (Input) 要产生随机数的个数R— Vector of length NR containing the random standard normal deviates. (Output)输出长度为NR，随机正态分布的向量Comments（注解）The routine RNSET can be used to initialize the seed of the random number generator. The routine RNOPT can be used to select the form of the generator.程序RNSET可以用来初始化随机数发生器的种子ExampleIn this example, RNNOA is used to generate five pseudorandom deviates from a standard normal distribution.INTEGER ISEED, NOUT, NRREAL R(5)EXTERNAL RNNOA, RNSET, UMACHCCALL UMACH (2, NOUT)NR = 5ISEED = 123457CALL RNSET (ISEED)CALL RNNOA (NR, R)WRITE (NOUT,99999) R99999 FORMAT (' Standard normal random deviates: ', 5F8.4)ENDOutputStandard normal random deviates: 2.0516 1.0833 0.0826 1.2777 -1.22603、RESHAPEIntrinsic Function（内部函数）Constructs an array of a specified shape from the elements of another array. 构造规定形式的数组Syntax（语法）result = RESHAPE (source, shape [ , pad][ , order])source(Input) Any type. Array whose elements will be taken in standard Fortran array order (see Remarks), and then placed into a new array.shape(Input) Integer. One-dimensional array that describes the shape of the output array created from elements of source. 描述输出数组的大小的一维数组，The elements of shape are the sizes of the dimensions of the reshaped array in order. If pad is omitted 省略, the total size specified by shape must be less than or equal to source.pad 可选参数(Optional; input) Same type as source. Must be an array. If there are not enough elements in source to fill the result array, elements of pad are added in standardFortran array order. If necessary, extra copies of pad are used to fill the array.order 可选参数(Optional; input) Integer. One-dimensional array. Must be the same length as shape.Permutes the order of dimensions in the result array. The value of order must be a permutation of (1, 2,...n) where n is the size of shape.Return Value（返回值）The result is an array the same data type and kind as source and a shape as defined in shape.ExamplesINTEGER AR1( 2, 5)REAL F(5,3,8)REAL C(8,3,5)AR1 = RESHAPE((/1,2,3,4,5,6/),(/2,5/),(/0,0/),(/2,1/))! returns 1 2 3 4 5! 6 0 0 0 0!! Change Fortran array order to C array orderC = RESHAPE(F, (/8,3,5/), ORDER = (/3, 2, 1/))END4、SUMIntrinsic Function（内部函数）Sums elements of an array or the elements along an optional dimension. The elements summed can be selected by an optional mask.将数组中的元素求和Syntax（语法）result = SUM (array [ , dim] [ , mask])array(Input) Integer, real, or complex. Array whose elements are to be summed.dim 可选参数(Optional; input) Integer. Dimension along which elements are summed.1 ≤dim≤n, where n is the number of dimensions in array.mask 可选参数(Optional; input) Logical. Must be same shape as array. If mask is specified, only elements in array that correspond to .TRUE. elements in mask are summed.Return Value（返回值）Same type and kind as array and equal to the sum of all elements in array or the sum of elements along dimension dim. If mask is specified, only elements that correspondto .TRUE. elements in mask are summed. Returns a scalar if dim is omitted or array is one-dimensional. Otherwise, returns an array one dimension smaller than array.ExamplesINTEGER array (2, 3), i, j(3)array = RESHAPE((/1, 2, 3, 4, 5, 6/), (/2, 3/))! array is 1 3 5! 2 4 6i = SUM((/ 1, 2, 3 /)) ! returns 6j = SUM(array, DIM = 1) ! returns [3 7 11]WRITE(*,*) i, jEND5、SEEDRun-Time Subroutine Changes the starting point of the pseudorandom number generator. 改变随机数发生器的起始点ModuleUSE MSFLIBSyntax（语法）CALL SEED (iseed)iseed(Input) INTEGER(4). Starting point for RANDOM.Remarks（注解）SEED uses iseed to establish the starting point of the pseudorandom number generator.A given seed always produces the same sequence of values from RANDOM.If SEED is not called before the first call to RANDOM, RANDOM always begins with a seed value of one. If a program must have a different pseudorandom sequence each time it runs, pass the constant RND$TIMESEED (defined in MSFLIB.F90) to the SEED routine before the first call to RANDOM.ExampleUSE MSFLIBREAL randCALL SEED(7531)CALL RANDOM(rand)6、RANDOMPurposeRun-Time Subroutine Returns a pseudorandom number greater than or equal to zero and less than one from the uniform distribution. 返回大于或等于0且小于1，服从均匀分布的随机数ModuleUSE MSFLIBSyntaxCALL RANDOM (ranval)ranval(Output) REAL(4). Pseudorandom number, 0 ≤ranval< 1, from the uniformdistribution.RemarksA given seed always produces the same sequence of values from RANDOM.If SEED is not called before the first call to RANDOM, RANDOM begins with a seed value of one. If a program must have a different pseudorandom sequence each time it runs, pass the constant RND$TIMESEED (defined in MSFLIB.F90) to SEED before the first call to RANDOM.All the random procedures (RANDOM, RAN, and RANDOM_NUMBER, and the PortLib functions DRAND, DRANDM, RAND, IRANDM, RAND, and RANDOM) use the same algorithms and thus return the same answers. They are all compatible and can be used interchangeably. (The algorithm used is a “Prime Modulus M Multiplicative Linear Congruential Generator,” a modified version of t he random number generator by Park and Miller in “Random Number Generators: Good Ones Are Hard to Find,” CACM, October 1988, Vol. 31, No. 10.)CompatibilityCONSOLE STANDARD GRAPHICS QUICKWIN GRAPHICS WINDOWS DLL LIBExampleUSE MSFLIBREAL(4) ranCALL SEED(1995)CALL RANDOM(ran)7、FFT2BCompute the inverse Fourier transform of a complex periodic two-dimensional array.计算二维复数数组的逆傅里叶变换Usage（用法）CALL FFT2B (NRCOEF, NCCOEF, COEF, LDCOEF, A, LDA)Arguments（参数）NRCOEF— The number of rows of COEF. (Input) 数组COEF的行数NCCOEF— The number of columns of COEF. (Input) 数组COEF的列数COEF—NRCOEF by NCCOEF complex array containing the Fourier coefficients to be transformed. (Input) NRCOEF行NCCOEF列数组LDCOEF— Leading dimension of COEF exactly as specified in the dimension statement of the calling program. (Input)A—NRCOEF by NCCOEF complex array containing the Inverse Fourier coefficients of COEF. (Output) NRCOEF行NCCOEF列复数数组，包含数组COEF的逆傅里叶系数LDA— Leading dimension of A exactly as specified in the dimension statement of the calling program. (Input)Comments（注解）1.Automatic workspace usage isFFT2B4 * (NRCOEF + NCCOEF) + 32 + 2 *MAX(NRCOEF, NCCOEF) units, orDFFT2B8 * (NRCOEF + NCCOEF ) + 64 + 4 *MAX(NRCOEF, NCCOEF) units.Workspace may be explicitly provided, if desired, by use of F2T2B/DF2T2B. The reference isCALL F2T2B (NRCOEF, NCCOEF, A, LDA, COEF, LDCOEF,WFF1, WFF2, CWK, CPY)The additional arguments are as follows:WFF1— Real array of length 4 *NRCOEF + 15 initialized by FFTCI. The initialization depends on NRCOEF. (Input)WFF2— Real array of length 4 *NCCOEF + 15 initialized by FFTCI. The initialization depends on NCCOEF. (Input)CWK— Complex array of length 1. (Workspace)CPY— Real array of length 2 *MAX(NRCOEF, NCCOEF). (Workspace)2.The routine FFT2B is most efficient when NRCOEF and NCCOEF are the product of small primes.3.The arrays COEF and A may be the same.4.If FFT2D/FFT2B is used repeatedly, with the same values for NRCOEF and NCCOEF, then use FFTCI to fill WFF1(N = NRCOEF) and WFF2(N = NCCOEF). Follow this with repeated calls to F2T2D/F2T2B. This is more efficient than repeated calls toFFT2D/FFT2B.AlgorithmThe routine FFT2B computes the inverse discrete complex Fourier transform of a complex two-dimensional array of size (NRCOEF = N) ⨯ (NCCOEF = M). The method used is a variant of the Cooley-Tukey algorithm , which is most efficient when N and M are both products of small prime factors. If N and M satisfy this condition, then the computational effort is proportional to N M log N M. This considerable savings has historically led people to refer to this algorithm as the "fast Fourier transform" or FFT.Specifically, given an N⨯M array c = COEF, FFT2B returns in aFurthermore, a vector of Euclidean norm S is mapped into a vector of normFinally, note that an unnormalized inverse is implemented in FFT2D. The routine FFT2B is based on the complex FFT in FFTPACK. The package FFTPACK was developed by Paul Swarztrauber at the National Center for Atmospheric Research.ExampleIn this example, we first compute the Fourier transform of the 5 ⨯ 4 arrayfor 1 ≤n≤ 5 and 1 ≤m≤ 4 using the IMSL routine FFT2D. The resultis then inverted by a call to FFT2B. Note that the result is an array a satisfying a = (5)(4)x = 20x. In general, FFT2B is an unnormalized inverse with expansion factor N M.INTEGER LDA, LDCOEF, M, N, NCA, NRACOMPLEX CMPLX, X(5,4), A(5,4), COEF(5,4)CHARACTER TITLE1*26, TITLE2*26, TITLE3*26INTRINSIC CMPLXEXTERNAL FFT2B, FFT2D, WRCRNCTITLE1 = 'The input matrix is below 'TITLE2 = 'After FFT2D 'TITLE3 = 'After FFT2B 'NRA = 5NCA = 4LDA = 5LDCOEF = 5C Fill X with initial dataDO 20 N=1, NRADO 10 M=1, NCAX(N,M) = CMPLX(FLOAT(N+5*M-5),0.0)10 CONTINUE20 CONTINUECCALL WRCRN (TITLE1, NRA, NCA, X, LDA, 0)CCALL FFT2D (NRA, NCA, X, LDA, COEF, LDCOEF)CCALL WRCRN (TITLE2, NRA, NCA, COEF, LDCOEF, 0)CCALL FFT2B (NRA, NCA, COEF, LDCOEF, A, LDA)CCALL WRCRN (TITLE3, NRA, NCA, A, LDA, 0)CENDOutputThe input matrix is below1 2 3 41 ( 1.00, 0.00) ( 6.00, 0.00) ( 11.00, 0.00) ( 16.00, 0.00)2 ( 2.00, 0.00) ( 7.00, 0.00) ( 12.00, 0.00) ( 17.00, 0.00)3 ( 3.00, 0.00) ( 8.00, 0.00) ( 13.00, 0.00) ( 18.00, 0.00)4 ( 4.00, 0.00) ( 9.00, 0.00) ( 14.00, 0.00) ( 19.00, 0.00)5 ( 5.00, 0.00) ( 10.00, 0.00) ( 15.00, 0.00) ( 20.00, 0.00) After FFT2D1 2 3 41 ( 210.0, 0.0) ( -50.0, 50.0) ( -50.0, 0.0) ( -50.0, -50.0)2 ( -10.0, 13.8) ( 0.0, 0.0) ( 0.0, 0.0) ( 0.0, 0.0)3 ( -10.0, 3.2) ( 0.0, 0.0) ( 0.0, 0.0) ( 0.0, 0.0)4 ( -10.0, -3.2) ( 0.0, 0.0) ( 0.0, 0.0) ( 0.0, 0.0)5 ( -10.0, -13.8) ( 0.0, 0.0) ( 0.0, 0.0) ( 0.0, 0.0) After FFT2B1 2 3 41 ( 20.0, 0.0) ( 120.0, 0.0) ( 220.0, 0.0) ( 320.0, 0.0)2 ( 40.0, 0.0) ( 140.0, 0.0) ( 240.0, 0.0) ( 340.0, 0.0)3 ( 60.0, 0.0) ( 160.0, 0.0) ( 260.0, 0.0) ( 360.0, 0.0)4 ( 80.0, 0.0) ( 180.0, 0.0) ( 280.0, 0.0) ( 380.0, 0.0)5 ( 100.0, 0.0) ( 200.0, 0.0) ( 300.0, 0.0) ( 400.0, 0.0)8、TIMEFPurposePortLib Function Returns the number of seconds since the first time it is called, or zero.ModuleUSE PORTLIBSyntaxresult=TIMEF ( )Return ValueREAL(8). Number of seconds that have elapsed since the first time TIMEF( ) was called. The first time called, TIMEF returns 0.0D0.CompatibilityCONSOLE STANDARD GRAPHICS QUICKWIN GRAPHICS WINDOWS DLL LIBExampleUSE PORTLIBINTEGER i, jREAL(8) elapsed_timeelapsed_time = TIMEF() DO i = 1, 100000j = j + 1END DOelapsed_time = TIMEF() PRINT *, elapsed_time END。

fortran 三角函数Fortran是一门古老的编程语言，最初由IBM公司在20世纪50年代开发。

它的全称是Formula Translation，因为最初它是用来进行科学和工程计算，特别是数值计算的语言。

Fortran具有很强的数学运算能力，自然而然地也就包含了各种三角函数的计算。

在Fortran中，三角函数可以使用数学库函数来计算。

Fortran的数学库包含了许多用于科学计算的函数，包括三角函数，对数函数，指数函数等等。

下面是Fortran中常见的三角函数及其用法：1. sin函数Sin函数可用于计算给定角度的正弦值。

Fortran命令为sin(x)，其中x是以弧度为单位的角度。

要计算30度的sin值，可以使用以下Fortran代码：program sin_exampleimplicit nonereal :: sin30sin30 = sin(30*3.14159/180)write(*,*) sin30end program sin_example在这个例子中，我们将30度的值转换为弧度，并将结果存储在sin30变量中。

我们输出sin30的值。

2. cos函数Cos函数可用于计算给定角度的余弦值。

Fortran命令为cos(x)，其中x是以弧度为单位的角度。

要计算60度的cos值，可以使用以下Fortran代码：program cos_exampleimplicit nonereal :: cos60cos60 = cos(60*3.14159/180)write(*,*) cos60end program cos_example在这个例子中，我们将60度的值转换为弧度，并将结果存储在cos60变量中。

我们输出cos60的值。

3. tan函数Tan函数可用于计算给定角度的正切值。

Fortran命令为tan(x)，其中x是以弧度为单位的角度。

要计算45度的tan值，可以使用以下Fortran代码：program tan_exampleimplicit nonereal :: tan45tan45 = tan(45*3.14159/180)write(*,*) tan45end program tan_example在这个例子中，我们将45度的值转换为弧度，并将结果存储在tan45变量中。

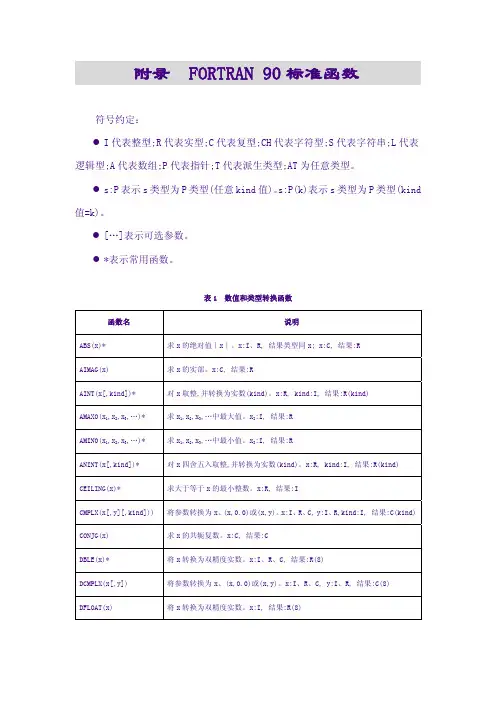
附录 FORTRAN 90标准函数符号约定：●I代表整型;R代表实型;C代表复型;CH代表字符型;S代表字符串;L代表逻辑型;A代表数组;P代表指针;T代表派生类型;AT为任意类型。

●s:P表示s类型为P类型(任意kind值)。

s:P(k)表示s类型为P类型(kind 值=k)。

●[…]表示可选参数。

●*表示常用函数。

表1 数值和类型转换函数函数名 说明ABS(x)* 求x的绝对值∣x∣。

x:I、R, 结果类型同x; x:C, 结果:RAIMAG(x) 求x的实部。

x:C, 结果:RAINT(x[,kind])* 对x取整,并转换为实数(kind)。

x:R, kind:I, 结果:R(kind)AMAX0(x1,x2,x3,…)* 求x1,x2,x3,…中最大值。

x I:I, 结果:RAMIN0(x1,x2,x3,…)* 求x1,x2,x3,…中最小值。

x I:I, 结果:RANINT(x[,kind])* 对x四舍五入取整,并转换为实数(kind)。

x:R, kind:I, 结果:R(kind) CEILING(x)* 求大于等于x的最小整数。

x:R, 结果:ICMPLX(x[,y][,kind])) 将参数转换为x、(x,0.0)或(x,y)。

x:I、R、C, y:I、R,kind:I, 结果:C(kind) CONJG(x) 求x的共轭复数。

x:C, 结果:CDBLE(x)* 将x转换为双精度实数。

x:I、R、C, 结果:R(8)DCMPLX(x[,y]) 将参数转换为x、(x,0.0)或(x,y)。

x:I、R、C, y:I、R, 结果:C(8) DFLOAT(x) 将x转换为双精度实数。

x:I, 结果:R(8)DIM(x,y)* 求x-y和0中最大值, 即MAX(x-y,0)。

x:I、R, y的类型同x,结果类型同x DPROD(x,y) 求x和y的乘积,并转换为双精度实数。

x:R, y:R, 结果:R(8)FLOAT(x)* 将x转换为单精度实数。

fortran getarg函数摘要：1.函数简介2.函数声明3.函数功能4.函数参数5.返回值6.应用示例正文：【1.函数简介】Fortran是一种高级编程语言，广泛应用于科学计算和工程领域。

在Fortran中，getarg函数是一个内置函数，用于获取调用程序时传递给子程序或函数的参数值。

它可以帮助我们在程序运行过程中获取外部输入的参数信息，以便进行相应的处理和计算。

【2.函数声明】getarg函数的声明如下：```function getarg(index, argcount)```其中，index表示要获取的参数索引，argcount表示传递给子程序或函数的参数总数。

【3.函数功能】getarg函数的主要功能是根据参数索引和参数总数，获取传递给子程序或函数的参数值。

它可以帮助我们在程序运行过程中获取外部输入的参数信息，以便进行相应的处理和计算。

【4.函数参数】getarg函数有两个参数：1.index：整数，表示要获取的参数索引。

参数索引从1开始，表示第一个参数。

如果提供负数索引，则从参数总数末尾开始计算。

例如，如果要获取第3个参数，可以传递1或3作为index参数。

2.argcount：整数，表示传递给子程序或函数的参数总数。

如果未提供argcount参数，则默认为1。

【5.返回值】getarg函数返回一个字符串，表示传递给子程序或函数的参数值。

如果参数索引超出范围或参数总数为0，则返回空字符串。

【6.应用示例】下面是一个简单的Fortran程序，展示了如何使用getarg函数获取传递给子程序的参数值：```fortranprogram mainimplicit noneinteger :: argcount = 0integer :: index = 1character(len=100) :: argvaluecall getarg(index, argcount)if (index > argcount) thenwrite(*,*) "参数索引超出范围"elseargvalue = getarg(index, argcount)write(*,*) "获取到的参数值：", argvalueendifcall getarg(3, argcount)if (index > argcount) thenwrite(*,*) "参数索引超出范围"elseargvalue = getarg(index, argcount)write(*,*) "获取到的参数值：", argvalueendifend program main```在这个示例中，我们首先定义了子程序main，并在其中声明了两个整数变量argcount和index，以及一个字符串变量argvalue。

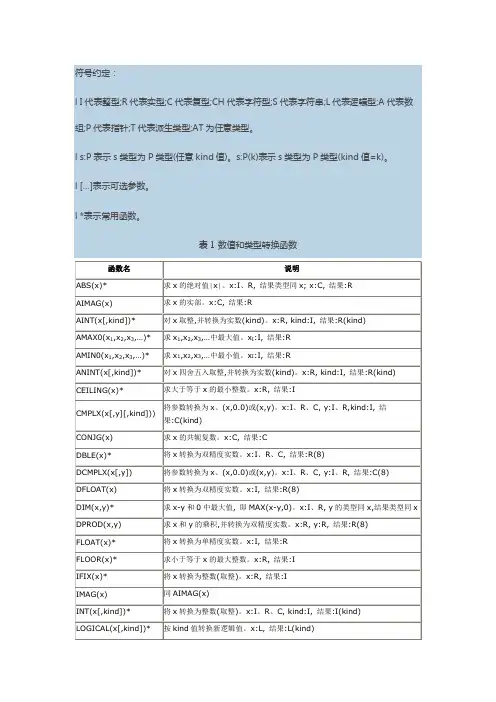
符号约定：
l I代表整型;R代表实型;C代表复型;CH代表字符型;S代表字符串;L代表逻辑型;A代表数组;P代表指针;T代表派生类型;AT为任意类型。

l s:P表示s类型为P类型(任意kind值)。

s:P(k)表示s类型为P类型(kind值=k)。

l […]表示可选参数。

l *表示常用函数。

表1 数值和类型转换函数
表2 三角函数
注：三角函数名前有C、D的函数为复数、双精度型函数。

表3 指数、平方根和对数函数
注：指数函数名、平方根函数名、对数函数名前有C、D的函数为复数、双精度型函数。

表4 参数查询函数
表5 实数检测和控制函数
表6 字符处理函数
表7 二进制位操作函数
表8 数组运算、查询和处理函数
注: 参数m指逻辑型掩码数组,指明允许操作的数组元素。

缺省掩码数组指对数组所有元素进行操作。