杨氏弹性模量数据

竭诚为您提供优质文档/双击可除杨氏模量实验报告数据篇一：杨氏模量实验报告杨氏模量的测量【实验目的】1．1．掌握螺旋测微器的使用方法。

2．学会用光杠杆测量微小伸长量。

3．学会用拉伸法金属丝的杨氏模量的方法。

【实验仪器】杨氏模量测定仪（包括：拉伸仪、光杠杆、望远镜、标尺），水准器，钢卷尺，螺旋测微器，钢直尺。

1、金属丝与支架（装置见图1）：金属丝长约0.5米，上端被加紧在支架的上梁上，被夹于一个圆形夹头。

这圆形夹头可以在支架的下梁的圆孔内自由移动。

支架下方有三个可调支脚。

这圆形的气泡水准。

使用时应调节支脚。

由气泡水准判断支架是否处于垂直状态。

这样才能使圆柱形夹头在下梁平台的圆孔转移动时不受摩擦。

2、光杠杆（结构见图2）：使用时两前支脚放在支架的下梁平台三角形凹槽内，后支脚放在圆柱形夹头上端平面上。

当钢丝受到拉伸时，随着圆柱夹头下降，光杠杆的后支脚也下降，时平面镜以两前支脚为轴旋转。

图1图2图33、望远镜与标尺（装置见图3）：望远镜由物镜、目镜、十字分划板组成。

使用实现调节目镜，使看清十字分划板，在调节物镜使看清标尺。

这是表明标尺通过物镜成像在分划板平面上。

由于标尺像与分划板处于同一平面，所以可以消除读书时的视差（即消除眼睛上下移动时标尺像与十字线之间的相对位移）。

标尺是一般的米尺，但中间刻度为0。

【实验原理】1、胡克定律和杨氏弹性模量固体在外力作用下将发生形变，如果外力撤去后相应的形变消失，这种形变称为弹性形变。

如果外力后仍有残余形变，这种形变称为塑性形变。

应力：单位面积上所受到的力（F/s）。

应变：是指在外力作用下的相对形变（相对伸长?L/L）它反映了物体形变的大小。

FL4FL?用公式表达为：Y??(1)s?L?d2?L2、光杠杆镜尺法测量微小长度的变化在（1）式中，在外力的F的拉伸下，钢丝的伸长量?L是很小的量。

用一般的长度测量仪器无法测量。

在本实验中采用光杠杆镜尺法。

初始时，平面镜处于垂直状态。

弯曲模量杨氏模量值在材料力学中，弯曲模量和杨氏模量是描述材料在受力时变形特性的两个重要参数。

它们分别反映了材料在弯曲和拉伸过程中的刚度，是工程设计和材料选择中不可或缺的参考指标。

一、弯曲模量概述弯曲模量，又称挠曲模量，是指材料在受力弯曲时，应力与应变之间的比例系数。

它反映了材料抵抗弯曲变形的能力，是评价材料弯曲刚度的重要指标。

在工程应用中，弯曲模量常用于计算梁、板等结构的弯曲变形和应力分布。

弯曲模量的测量通常采用三点弯曲试验或四点弯曲试验。

在这些试验中，试样被放置在两个支点之间，并在试样中央施加集中载荷。

通过测量试样在载荷作用下的挠度（变形量），结合试样的几何尺寸和载荷大小，可以计算出材料的弯曲模量。

二、杨氏模量概述杨氏模量，又称拉伸模量或弹性模量，是指材料在受拉伸力时，应力与应变之间的比例系数。

它反映了材料抵抗拉伸变形的能力，是评价材料拉伸刚度的重要指标。

在工程应用中，杨氏模量广泛用于计算杆、轴等结构的拉伸变形和应力分布。

杨氏模量的测量通常采用拉伸试验。

在拉伸试验中，试样被夹持在试验机的夹具之间，并施加逐渐增大的拉伸力。

通过测量试样在拉伸过程中的伸长量（变形量），结合试样的原始尺寸和拉伸力大小，可以计算出材料的杨氏模量。

三、弯曲模量与杨氏模量的区别与联系虽然弯曲模量和杨氏模量都是描述材料变形特性的参数，但它们在物理意义、测量方法以及工程应用等方面存在显著差异。

1. 物理意义不同：弯曲模量描述的是材料在弯曲过程中的刚度，而杨氏模量描述的是材料在拉伸过程中的刚度。

这意味着两者分别反映了材料在不同受力状态下的变形行为。

2. 测量方法不同：弯曲模量通常通过三点弯曲试验或四点弯曲试验来测量，而杨氏模量则通过拉伸试验来测量。

这两种试验方法在试样的准备、加载方式以及变形量的测量等方面都有所不同。

3. 工程应用不同：由于弯曲模量和杨氏模量分别反映了材料在弯曲和拉伸过程中的变形特性，因此它们在工程应用中的侧重点也有所不同。

第1篇一、杨氏模量的概念杨氏模量（Young's Modulus），又称弹性模量，是材料在受到外力作用时，材料内部应力与应变的比值。

其单位为帕斯卡（Pa）或兆帕（MPa）。

杨氏模量越大，材料抵抗形变的能力越强。

二、不同材料的杨氏模量1. 金属材料的杨氏模量金属材料的杨氏模量普遍较高，这是因为金属原子之间具有较强的金属键。

以下是一些常见金属材料的杨氏模量：（1）钢：杨氏模量约为200 GPa；（2）铝：杨氏模量约为70 GPa；（3）铜：杨氏模量约为110 GPa；（4）钛：杨氏模量约为110 GPa；（5）镍：杨氏模量约为200 GPa。

2. 非金属材料的杨氏模量非金属材料的杨氏模量相对较低，但也有一些材料的杨氏模量较高。

以下是一些常见非金属材料的杨氏模量：（1）玻璃：杨氏模量约为60 GPa；（2）陶瓷：杨氏模量约为200-400 GPa；（3）塑料：杨氏模量较低，一般在1-5 GPa之间；（4）木材：杨氏模量约为10-20 GPa；（5）橡胶：杨氏模量较低，一般在0.01-0.1 GPa之间。

3. 复合材料的杨氏模量复合材料是由两种或两种以上不同性质的材料组成的。

复合材料的杨氏模量取决于组成材料的杨氏模量和各组分材料之间的界面强度。

以下是一些常见复合材料的杨氏模量：（1）碳纤维增强塑料：杨氏模量约为200-400 GPa；（2）玻璃纤维增强塑料：杨氏模量约为40-60 GPa；（3）碳纤维增强金属：杨氏模量约为200-400 GPa；（4）玻璃纤维增强金属：杨氏模量约为100-200 GPa。

三、影响杨氏模量的因素1. 材料的内部结构：原子、分子或晶体的排列方式对杨氏模量有较大影响。

例如，金属材料的杨氏模量较高，因为金属原子之间具有较强的金属键。

2. 材料的组成：不同元素的原子半径、电子排布和化学性质等因素都会影响杨氏模量。

3. 材料的加工工艺：材料的加工工艺，如热处理、冷加工等，会影响其内部结构和性能，进而影响杨氏模量。

q390的杨氏模量杨氏模量是材料力学性质中的一个重要参数，也称为弹性模量或弹性系数，一般用符号E表示，单位为帕斯卡（Pa）。

杨氏模量是描述材料在外力作用下产生弹性变形的能力的指标。

它是指材料在线弹性阶段内，单位应力作用下，产生的相对应力增量与相对应变增量之比。

也就是说，杨氏模量反映了材料因外力作用产生的弹性变形程度。

杨氏模量最早由英国科学家托马斯·杨在19世纪提出，并在他的名字中命名。

杨氏模量的计算可以通过拉伸试验来得到，通过测量材料在拉伸力作用下的长度变化和断裂前的横截面积来计算。

杨氏模量的计算公式为：E = (F/A) / (ΔL/L)其中，E为杨氏模量，F为外力，A为截面积，ΔL为长度变化，L 为原始长度。

杨氏模量与材料的性质有密切关系。

对于不同的材料，其杨氏模量也不同。

一般来说，杨氏模量越大，材料的刚度越高，也就是其抵抗外力形变的能力越强。

相反，如果杨氏模量较小，材料的刚度就不太高，容易发生形变。

$q390是一种高强度低合金结构钢，常用于构筑物、桥梁、船舶等工程领域。

作为一种高强度钢材，q390的杨氏模量也相对较高。

实际上，q390的杨氏模量通常在190GPa以上，具有较好的刚度和抗弯强度。

高强度低合金结构钢的杨氏模量通常比一般碳素钢高，这是因为高强度钢具有更高的强度和刚性，能够承受更大的外力而产生较小的变形。

在工程领域，这种高强度材料能够提供更好的结构支撑性能，减少结构的振动和变形。

然而，需要注意的是，q390的杨氏模量与其他因素也有关系。

例如，温度会对杨氏模量产生一定的影响。

在低温环境下，杨氏模量往往会有所增加，这是因为低温会使材料分子结构紧密，分子的振动范围减小，从而增加材料的弹性。

此外，q390的杨氏模量还会受到材料的组织结构和冷处理等技术因素的影响。

通过优化材料的处理工艺，可以进一步提高杨氏模量。

总之，q390作为一种高强度低合金结构钢，具有较高的杨氏模量。

这使得它在工程领域中应用广泛，能够满足各种结构的要求。

实验二杨氏弹性模量的测定杨氏弹性模量是描述材料形变能力的重要物理量，是选定机械零件材料的依据之一，是工程技术没计中常用的参数．杨氏模量的测量方法很多，本实验采用光杠杆测量金属丝的杨氏弹性模量。

测量中需综合运用多种测量长度的量具，确保一定的精确度要求，学习从误差分析的角度，选用最合适的量具，并要求用不确定度表示完整的测量结果。

用一般测量长度的工具不易精确测量长度的微小变化，也难保证其精度要求。

光杠杆是一种应用光放大原理测量被测物微小长度变化的装置，它的特点是直观、简便、精度高。

目前光杠杆原理已被广泛地应用于其他测量技术中，光杠杆装置还被许多高灵敏度的测量仪器(如灵敏电流计、冲击电流计和光点检流计等)用来显示微小角度的变化。

【实验目的】1.学会用拉伸法测定杨氏弹性模量；2.掌握光杠杆测量微小长度变化的原理和力法；3.学会用逐差法处理实验数据，学会用不确定度的计算方法，结果的正确表达；【实验仪器】杨氏模量测定仪、千分尺、游标卡尺、钢卷尺等【实验原理】在外力作用下，固体所发生的形状变化，称为形变。

形变可分为弹性形变与塑性形变两大类。

外力撤除后物体能完全恢复原状的形变，称为弹性形变，如外力撤除后物体不能完全恢复原状，而留下剩余形变，就称为塑性形变。

本实验只研究弹性形变，因此，应当控制外力的大小，以保证外力撤除后物体能恢复原状。

一根均匀的金属丝(或棒)，长为L ，截面面积为S ，在受到沿长度方向的外力F 的作用时发生形变，伸长L ∆。

根据胡克定律，在弹性限度内，其应力F S 与应变L L ∆成正比，即LL E S F ∆=(1)这里的E 称为该金属丝的杨氏模量。

它只决定于材料的性质，而与其长度L 、截面面积S 无关。

它的单位为2N/m 。

设金属丝的直径为d ，则截面面积214S d π=，其杨氏模量为24FL E d Lπ=∆(2)这里F 、L 、d 可以直接测得，L ∆采用光杠杆法测量。

光杠杆和标尺是光杠杆法测量L ∆的主要仪器，光杠杆是由一块直立的平面镜装在三足支架的一端构成，其放置方法如下图所示。

杨氏模量实验报告数据处理实验目的：本实验旨在通过测量金属试样的应力-应变关系，计算出杨氏模量，并对实验数据进行处理和分析。

实验原理：杨氏模量是描述材料抗弯刚度的物理量，定义为单位面积内所受的拉应力与相应的拉应变之比。

实验中，我们采用了悬臂梁法来测量杨氏模量。

实验步骤：1. 准备工作：a. 清洁并测量金属试样的尺寸，记录下其长度L、宽度W和厚度H。

b. 将金属试样固定在实验台上，使其成为一个悬臂梁。

2. 实验测量：a. 在试样上标出若干个等距离的测量点，用游标卡尺测量每个测量点的位置距离试样固定点的距离x。

b. 使用力传感器测量每个测量点处的挠度d。

c. 记录下每个测量点处施加的力F。

3. 数据处理：a. 计算每个测量点处的应力σ，公式为：σ = F / (W * H)。

b. 计算每个测量点处的应变ε，公式为：ε = d / L。

c. 绘制应力-应变曲线图，横轴为应变ε，纵轴为应力σ。

d. 选择直线段，根据线性回归方法计算出斜率k，即弹性模量E。

e. 计算杨氏模量Y，公式为：Y = E / (1 - ν^2)，其中ν为泊松比。

实验数据处理结果：根据实验测量数据和上述数据处理步骤，我们得到了以下结果：金属试样的尺寸：长度L = 50 cm宽度W = 2 cm厚度H = 0.5 cm实验测量数据：测量点位置距离试样固定点的距离x (cm) 挠度d (mm) 施加力F (N) ----------------------------------------------0.00 0.00 0.005.00 0.02 0.1010.00 0.05 0.2015.00 0.09 0.3020.00 0.14 0.4025.00 0.19 0.50数据处理：根据上述实验测量数据，我们可以计算得到应力σ和应变ε：测量点位置距离试样固定点的距离x (cm) 应力σ (MPa) 应变ε----------------------------------------------0.00 0.00 0.0005.00 0.50 0.000410.00 1.00 0.00115.00 1.50 0.001820.00 2.00 0.002625.00 2.50 0.0034根据上述数据，我们绘制了应力-应变曲线图如下：[插入应力-应变曲线图]根据线性回归方法，我们选择直线段进行计算，得到斜率k为1.25 MPa/mm。

金属丝的杨氏模量大小一般多大
金属丝的杨氏模量大致范围是1.1×1011N·m-2。

铜的杨氏模量为2.0×1011N·m-2.从此可以推出其它金属的杨氏模量的数量级，具体要计算时，可以查村水裂金属手册，更精确、权威，杨氏模量是描述固体材料抵抗变能力的物理量，杨氏模量衡量的是一个各向同性弹性体的刚度。

金属丝的定义
金属丝的杨氏模量大概是2.0乘以10的11次方牛米负二次方，杨氏模量是描述固体材料抵抗变能力的物理量，杨氏模量衡量的是一个各向同性弹性体的刚度，钢丝是钢材的板、管、型四大品种之一，是用热续下富干围度轧盘条经冷拉制成的再加工产品。

杨氏弹性模量是选定机械零件材料的依据之一，是工程技术设计中常用的参数。

杨氏模量的测定对研究金属材料、光纤材料、半导体、纳米材料、聚合物、陶瓷画济利送船乐、橡胶等各种材料的力学性质有着重要意义，还可用于机械互功推零部件设计、生物力学、地质等领域。

一、引言固体材料受外力作用时必然发生形变，其内部胁强（单位面积上受力大小）和胁变（即相对形变）的比值称为杨氏弹性模量，这是衡量固体材料受力后形变大小的参数之一，是设计各种工程结构时选用材料的主要依据之一。

本实验需要掌握伸长法（读数显微镜配以CCD成象系统）和弯曲法两种测量方法，其中涉及了卷尺、千分尺、游标卡尺和读数显微镜的正确使用，并且综合了逐差法、线性拟合法来进行数据处理及不确定度的计算，是一个经典的力学物理实验。

二、实验原理1.伸长法：胡克定律指出，在弹性限度内，弹性体的应力和应变成正比。

设有一根长为L 横截面积为S的钢丝，在外力F作用下伸长了δ，则F/S=Eδ/L (1) ; 式中的比例系数E称为杨氏模量，单位为N.m-2。

设钢丝直径为d，则，将此代入上式并整理后得出E=4FL/(πd2δ) (2);上式表明，对于长度L、直径d和所加外力F相同的情况下，杨氏模量大的金属丝的伸长量δ较小，而杨氏模量小的伸长量较大。

因而，杨氏模量表达了材料抵抗外力产生拉伸（或压缩）形变的能力。

根据式（2）测杨氏模量时，伸长量δ比较小不易测准，本实验采用了读数显微镜配以CCD成象系统测量钢丝微小的伸长量。

呈像系统总的放大率为62.5倍。

2.弯曲法：在衡量歪曲时杨氏模量的表示公式为：E=(d3mg)/(4a3bΔZ); 其中d为两刀口间的距离，a为梁的厚度，b为梁的宽度，m为加挂砝码的质量，ΔZ为梁中心由于外力作用而下降的作用，g为当地的重力加速度。

实验时我们利用读数显微镜来测量梁中心下降的距离。

（关于歪曲法杨氏模量的推导附于报告最后）三、实验器材及实验过程实验器材：伸长法：千分尺、卷尺、金属丝支架（编号：20011664）、读数显微镜及CCD呈像显示系统（编号：D2*******）；歪曲法：FD-HY-I杨氏模量实验仪（编号：20036985），千分尺，游标卡尺，不锈钢直尺，黄铜片，钢片等；DC12V监视器CCD MS测试样品H2H1伸长法实验图像实验过程：（由于具体的在预习报告中以写明，故在此简略些）实验1：1)调节金属丝铅直，正确调节显微物镜的目镜、物镜及摄像机镜头后在监视器屏带上看到清晰的图像。

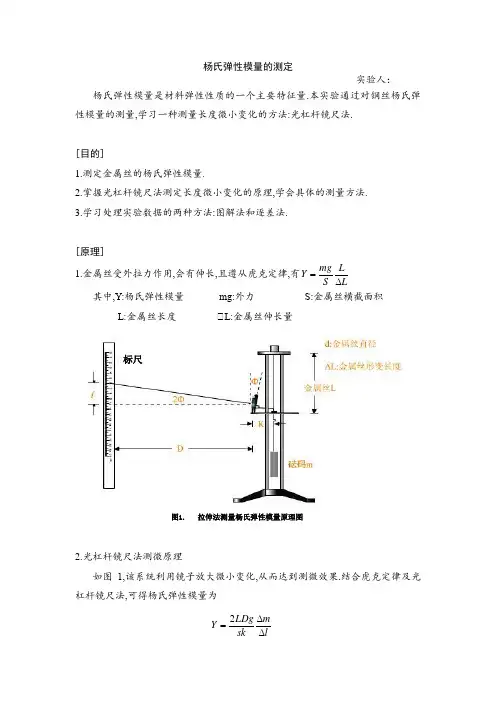
杨氏弹性模量的测定实验人：杨氏弹性模量是材料弹性性质的一个主要特征量.本实验通过对钢丝杨氏弹性模量的测量,学习一种测量长度微小变化的方法:光杠杆镜尺法.[目的]1.测定金属丝的杨氏弹性模量.2.掌握光杠杆镜尺法测定长度微小变化的原理,学会具体的测量方法.3.学习处理实验数据的两种方法:图解法和逐差法. [原理]1.金属丝受外拉力作用,会有伸长,且遵从虎克定律,有LLS mg Y ∆=其中,Y:杨氏弹性模量 mg:外力 S:金属丝横截面积 L:金属丝长度 △L:金属丝伸长量2.光杠杆镜尺法测微原理如图1,该系统利用镜子放大微小变化,从而达到测微效果.结合虎克定律及光杠杆镜尺法,可得杨氏弹性模量为图1. 拉伸法测量杨氏弹性模量原理图标尺lm sk LDg Y ∆∆=2其中,L:金属丝原长 D:镜面到标尺的垂直距离 S:金属丝截面积 K:光杠杆前足到两后足连线的垂直距离 m ∆:单个砝码质量l ∆:加/减单个砝码时，标尺读数变化量LDgSK 均为常量,l m ∆∆/由图解法和逐差法求出 [仪器]杨氏模量测定仪(如图M-4-3),调节方法如下:1.调节光杠杆与望远镜在同一高度,光杠杆镜面尽可能铅直.2.在望远镜外侧寻找光杠杆镜面上标尺的象(如看不到,应调节镜面方位和移动测定仪的位置)3.移动望远镜,使其缺口与准星大致对准标尺的像.4.调节望远镜目镜,使观察到的十字叉丝清晰.5.调节望远镜调焦手轮,先观察到镜子，再观察到标尺，使观察到的标尺读数与十字叉丝均清晰而无视差.[实验步骤]1.调节测定仪,使支架铅直.2.在金属丝下端先挂一负载(如2千克),使金属丝完全拉直,此负载为初始负载,不计入作用力内.3.用带有卡具的米尺量出金属丝长度L.4.在不同位置，用螺旋测微计测10次金属丝直径d,取平均值.5.安装光杠杆,调节望远镜,记录望远镜读数x 0,逐渐增加砝码到9×0.500kg,每次增加0.500kg,记录望远镜读数x i ’,再逐渐减少砝码,记录望远镜读数,则x i =0.5(x i ’+ x i ’’)6.用钢皮尺测量光杠杆镜面到标尺的距离D7.用游标卡尺测量光杠杆前足到后两足连线的垂直长度K.[注意事项]1.调节望远镜时,注意消除视差,即要求标尺读数相对十字叉丝无相对位移.2.实验前,望远镜中标尺读数应在10~20cm 之间.3.在测量期间切不可碰撞或移动仪器.4.不可触摸光杠杆镜面.[数据记录和处理] 金属丝材料：钢5块砝码质量：m=5×0.500kgcm K cm D D D cm L L L 280.70.1750.882121==-==-= g=9.794m/s 2最大仪器误差 不确定度m ：砝码，0.500kg ， 2g g U m 63/25=⨯≈ L ：米尺，分度1mm cm U L 2.0≈ D ：钢卷尺，分度1mm ， cm U D 4.0≈ K ：游标卡尺，分度0.02mm cm U k 01.0≈d ：千分尺，分度0.004mm 0.004mm m m n n v U i d 003.0))1(()3004.0(222=-+≈∑ i i l l -+5：米尺，分度1mm 0.1cm cm n n vU il 06.0))1(()31.0(222=-+=∑1.测定金属丝的直径（mm ）:d=(0.493±0.003)mm (螺旋测微计标准仪器偏差为0.002mm) 2.测定钢丝的l m ∆∆/ 值:3.计算钢丝的杨氏弹性模量钢丝的杨氏弹性模量标准值：Y’=2.00×1011N/m 2 （1）用逐差法处理实验数据： 平均值cm l l i i 83.25=-+l m /=cm kg /883.083.2500.05=⨯=88.3kg/m 钢丝的杨氏弹性模量为2112224/1092.110883.01028.7)1093.4(794.9750.1880.082m N l m sk LDg Y ⨯=⨯⋅⨯⨯⨯⨯⨯⨯⨯==--π %3,/10)05.092.1(/1005.0%3)()()2()()()(211211222222=⨯±=⨯=⋅==+++++==rY rY Y l m d K D L Y rY U m N Y m N Y U U l U m U d U K U D U L U Y U U 则钢丝杨氏弹性模量百分差%4%100''0=⨯-=Y Y Y E(1) 用图解法处理实验数据如图为m-l 关系曲线，利用图线求出比值m/l : 直线斜率为m/l =0.879kg/cm 钢丝的杨氏弹性模量为 Y 1=(8LDgm)/(πd 2K l )=2241028.7)1093.4(794.9750.1880.08--⨯⨯⨯⨯⨯⨯⨯π×0.879×102=1.91×1011N/m 2 百分差%4%100''0=⨯-=Y Y Y E[思考题]1.作图法和逐差法处理实验数据各有什么特点?答:作图法特点是简单,直观,明显表达实验数据间关系.作图法最常用的是作直线.逐差法的特点是可以充分利用实验数据,合理减小实验误差.但逐差法必须满足三个条件:两个变量间存在多项式函数关系;自变量成等差级数递增或递减;测得的数据为偶数组.2.请分析那些原因会造成x i ’, x i ’’相差较大?答:可能的原因有:金属丝本身不直;杨氏弹性模量仪支柱不垂直,因而摩擦阻力较大;光杠杆尖角与金属丝相碰;测试时移动光杠杆等.3.实验中为什么用不同的长度测量仪器分别测量各量?答:由误差分析可知,各物理量的相对误差不一样,对误差项大的要选择较好的仪器, 对误差项小的要选择较一般的仪器,才能保证相对误差相近,以免做无谓的测量.。

用一般测量长度的工具不易精确测量长度的微小变化，也难保证其精度要求。光杠杆是
一种应用光放大原理测量被测物微小长度变化的装置，它的特点是直观、简便、精度高。目
前光杠杆原理已被广泛地应用于其他测量技术中，光杠杆装置还被许多高灵敏度的测量仪器
(如灵敏电流计、冲击电流计和光点检流计等)用来显示微小角度的变化。
减重时读 数 Ri(cm)
1.00
—0.01
—0.05
两次读数的 平均值
Ri (cm)
—0.03
2.00
0.88
0.92
0.90
3.00
1.83
1.91
1.87
4.00
2.81
2.88
2.84
5.00
3.77
3.75
3.76
6.00
4.74
——
4.74
每增重 3kg 时读 数差 Ni(cm)
N1R4 R12.87
分别记录相应的标尺读数。
逐次增加1kg 的砝码，共 6 次。依次记下每一次标尺读数 R1 、 R2 、……、 R6 。再逐次 减去1kg 砝码，测得相应的读数 R5 、… R1 ，记入表 2。
读出尺度望远镜中的上丝、下丝读数，计算出光杠杆镜面到标尺距离 D D 50 上丝读数-下丝读数
50 —2.19 cm — 2.18 cm
光杠杆镜面到标尺的距离的不确定度U D U B 仪 0.01cm
218.50cm
次序
1 2 3 4 5
6
表 2：标尺士数及数据处理
砝码重
F (9.8N )
增重时读 数 Ri(cm)
【实验目的】
1.学会用拉伸法测定杨氏弹性模量；

杨氏弹性模量的测定实验报告一、实验目的1、学习用拉伸法测定金属丝的杨氏弹性模量。

2、掌握用光杠杆法测量微小长度变化的原理和方法。

3、学会使用望远镜、标尺、螺旋测微器等测量长度的仪器。

4、学会用逐差法处理实验数据。

二、实验原理1、杨氏弹性模量杨氏弹性模量是描述固体材料抵抗形变能力的物理量。

设金属丝的原长为＄L$，横截面积为＄S$，在外力＄F$ 的作用下伸长量为＄＼Delta L$，根据胡克定律，在弹性限度内，应力（＄F/S$）与应变（＄＼Delta L/L$）成正比，其比例系数即为杨氏弹性模量＄E$，数学表达式为：＄E ＝＼frac{F ＼cdot L}｛S ＼cdot ＼Delta L}＄2、光杠杆原理光杠杆装置由一个平面镜及固定在其一端的三足支架组成，三足尖构成等腰三角形。

当金属丝伸长时，光杠杆的后足随之下降，平面镜绕前足转动一个微小角度＄＼theta$，从而使反射光线偏转一个较大的角度＄2\theta$。

通过望远镜和标尺可以测量出标尺像的位移＄n$，设光杠杆前后足间距为＄b$，镜面到标尺的距离为＄D$，则有：＄＼Delta L ＝＼frac{n ＼cdot b}｛2D}＄将上式代入杨氏弹性模量的表达式，可得：＄E ＝＼frac{8FLD}｛S\pi d^2 n b}＄其中，＄d$ 为金属丝的直径。

三、实验仪器杨氏模量测定仪、光杠杆、望远镜及标尺、螺旋测微器、游标卡尺、砝码、米尺等。

四、实验步骤1、调节仪器（1）调节杨氏模量测定仪底座的水平调节螺丝，使立柱铅直。

（2）将光杠杆放在平台上，使平面镜与平台垂直，三足尖位于同一水平面，且三足尖与平台的接触点构成等边三角形。

（3）调节望远镜，使其与光杠杆平面镜等高，且望远镜光轴与平面镜中心等高。

然后通过望远镜目镜看清十字叉丝，再将望远镜对准平面镜，调节目镜和物镜，直至能在望远镜中看到清晰的标尺像。

（4）调节标尺的位置，使其零刻度线与望远镜中十字叉丝的横线重合。

实验名称：杨氏弹性模量的测定【实验目的】1、掌握伸长法测量金属丝杨氏模量的原理和方法；2、掌握用光杠杆测量长度微小变化量的原理和方法；3、学习光杠杆和尺度望远镜的调节与使用；4、学习处理数据的方法。

【实验仪器】杨氏模量测定仪 光杠杆 尺度显微镜 钢卷尺 游标卡尺 螺旋测微计 砝码 金属丝【实验原理】1、杨氏模量设一粗细均匀的金属丝长为l ，截面积为S ，上端固定，下端悬挂砝码，金属丝在外力F 的作用下发生形变，伸长l δ。

根据胡克定律，在弹性限度内，金属丝的胁强F S和产生的胁变lLδ成正比。

即F lE S l δ= （9-1） 或 FlES lδ=（9-2） 式中比例系数E 称为杨氏弹性模量。

在国际单位制中，杨氏弹性模量的单位为牛每平方米，记为2-⋅m N 。

在实验中测量钢丝的杨氏模量，其截面为圆形，其直径为d 时，相应的截面积4/2d S π=，l δ是较大长度的微小伸长量，无法用一般的长度测量仪器测量，因此实验中用光杠杆法进行测量，测量公式 0122m A A d l d δ-=于是可得实验中的杨氏模量测量公式： 22018m mgld E d A A d π=-令0m A A K m-=，K 为砝码质量改变一个单位时，望远镜中所见尺的读数的变化量，则2218gld E d Kd π=2、光杠杆实验中l δ是一微小变化量，变化在mm 210-数量级。

因此实验设计的关键是寻找测量微小变化量的方法和装置，这里我们采用了光路放大方法——光杠杆来实现。

设未加砝码时，从望远镜中读得标尺读数记为0A ，当增加砝码时， 钢丝伸长量为l δ，光杠杆一端随圆柱体夹头一起下降，光杠杆的转角θ，于是光杠杆镜面法线轴转动θ角。

根据反射定律，平面镜法线转动θ角，反射线将转过θ2，此时从望远镜中读得的标尺读数为m A 。

因为l δ为一微小量，所以θ也很小，近似有θθtg ≈和θθ22tg ≈。

于是由三角函数关系可得：122m A A ld d δ-=由于2d 远大于1d ，则0m A A -必然远大于l δ。

数据处理杨氏弹性模量杨氏弹性模量，也称杨氏模量或弹性模量，是材料力学中的一个重要参数。

它描述了材料在承受一定的拉伸、压缩或弯曲载荷后，相应的单向应力与应变之间的比值。

杨氏弹性模量是材料刚度的量度，是一个特定材料的弹性性和变形能力的度量。

杨氏弹性模量的单位是帕斯卡（Pa），通常用千兆帕（GPa）表示，即每平方英寸承受1000万磅的力所产生的应变。

由于杨氏弹性模量没有方向性，因此可以用于描述材料在各个方向上的应变响应。

杨氏弹性模量与其他材料参数的关系在材料力学中，杨氏弹性模量与其他材料参数之间存在着一定的关系，其中比较重要的包括：1. 剪切模量：剪切模量（也称剪切弹性模量）是描述材料在剪切应力作用下的弹性特性的材料参数。

它与杨氏弹性模量之间的关系为：杨氏弹性模量E和剪切模量G的关系可以表示为：G = E/（2（1+μ)）；其中，μ为泊松比。

泊松比表示某个材料在受力时体积的压缩变化率与横向尺寸的比值。

材料弹性学中的主要参数1. 横向柔度：横向柔度表示单位横向应力下的单位横向应变。

它与杨氏弹性模量的关系为：横向柔度 = 1 / E；3. 线膨胀系数：线膨胀系数描述单位温度变化下材料线膨胀量与长度之比。

它与杨氏弹性模量、体积模量和泊松比之间的关系为：热膨胀系数 = （3α / K）；其中，α为线膨胀系数。

数据处理方法使用杨氏弹性模量来描述材料的弹性特性是材料力学中最基本的方法之一。

在实际应用中，我们可以使用以下方法来处理杨氏弹性模量的数据：1. 实验测定：实验测定是确定杨氏弹性模量的主要方法。

它涉及到试样制备、试验装置设置和数据处理等方面。

在实验中，我们通常采用拉伸、压缩或弯曲的方式来测定杨氏弹性模量。

通过实验测定得到的弹性模量是一个比较准确且可靠的数值。

2. 理论计算：杨氏弹性模量和其他材料参数之间具有一定的关系，因此我们也可以使用理论计算的方法来估计弹性模量。

理论计算主要涉及到分子动力学、第一原理计算、经验公式和统计方法等方面。

杨氏模量的值大约是多少
杨氏模量的值大约是多少：钢的杨氏模量为1.1×1011 N·m-2,铜的杨氏模量为2.0×1011 N·m-2.
杨氏弹性模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量，它是沿纵向的弹性模量，也是材料力学中的名词。

1807年因英国医生兼物理学家托马斯·杨(Thomas Young, 1773-1829) 所得到的结果而命名。

根据胡克定律，在物体的弹性限度内，应力与应变成正比，比值被称为材料的杨氏模量，它是表征材料性质的一个物理量，仅取决于材料本身的物理性质。

杨氏模量的大小标志了材料的刚性，杨氏模量越大，越不容易发生形变。

杨氏模量是应力/应变之比，单位是Pa(N/m^2)或
MPa(MN/m^2;N/mm^2)
杨氏弹性模量是选定机械零件材料的依据之一是工程技术设计中常用的参数。

杨氏模量的测定对研究金属材料、光纤材料、半导体、纳米材料、聚合物、陶瓷、橡胶等各种材料的力学性质有着重要意义，还可用于机械零部件设计、生物力学、地质等领域。

测量杨氏模量的方法一般有拉伸法、梁弯曲法、振动法、内耗法等，还出现了利用光纤位移传感器、莫尔条纹、电涡流传感器和波动传递技术（微波或超声波）等实验技术和方法测量杨氏模量。

1。

实验二杨氏弹性模量的测定实验报告一、实验目的1、学会用伸长法测量金属丝的杨氏弹性模量。

2、掌握光杠杆测量微小长度变化的原理和方法。

3、学会使用游标卡尺、螺旋测微器等测量长度的仪器。

4、学会用逐差法处理实验数据。

二、实验原理1、杨氏弹性模量杨氏弹性模量是描述固体材料抵抗形变能力的物理量。

对于一根粗细均匀的金属丝，在其长度方向上施加拉力 F，金属丝会发生伸长，伸长量为ΔL。

根据胡克定律，在弹性限度内，应力与应变成正比，即：＼F ＝ Y\frac{＼Delta L}｛L}＼其中，Y 为杨氏弹性模量，L 为金属丝的原长。

2、光杠杆原理光杠杆是一个带有三个尖足的平面镜，前两尖足放在一个平台上，后尖足置于一个可移动的小立柱上。

当金属丝发生微小伸长时，光杠杆的后尖足会随之移动，从而带动平面镜转动一个微小角度θ。

设平面镜到标尺的距离为D，光杠杆的长臂长度为b，金属丝的伸长量为ΔL，则有：＼＼tan\theta ＼approx ＼theta ＝＼frac{＼Delta L}｛b}＼由于θ很小，反射光线在标尺上的移动距离Δn 与θ的关系为：＼＼Delta n ＝ D\theta ＼approx ＼frac{D\Delta L}｛b}＼从而可得：＼＼Delta L ＝＼frac{b\Delta n}｛D}＼将其代入胡克定律，可得杨氏弹性模量的表达式为：＼Y ＝＼frac{8FLD}｛＼pi d^2 b\Delta n}＼其中，d 为金属丝的直径。

三、实验仪器1、杨氏弹性模量测定仪包括光杠杆、望远镜和标尺组成的光杠杆系统，以及用于加力的砝码和托盘。

2、螺旋测微器用于测量金属丝的直径。

3、游标卡尺用于测量光杠杆的长臂长度 b 和平面镜到标尺的距离 D。

4、米尺用于测量金属丝的原长 L。

四、实验步骤1、仪器调节（1）调节杨氏弹性模量测定仪，使金属丝竖直且与平台垂直，光杠杆平面镜与平台平行。

（2）调节望远镜，使其与光杠杆平面镜等高，且能清晰看到标尺的像。

pla的杨氏模量杨氏模量是杨氏弹性模量的简称，是表示材料在受力下的弹性特性的重要参数之一。

它可以用来衡量材料在承受外力时的变形程度和恢复能力，也可以用来比较材料的硬度和刚度。

杨氏模量通常用符号E 表示，是一个量纲为N/m²（帕斯卡）、等于外力单位面积的应变所产生的应力的比值。

杨氏模量最早由18世纪的英国科学家托马斯·杨提出，被广泛应用在材料力学、工程力学和地球物理等领域中。

它是描述材料在弹性变形过程中的抵抗性能的一项重要参数，对于工程设计和材料选择具有重要意义。

杨氏模量的定义可以表示为：E = (F/A) / (δL/L0)其中E为杨氏模量，F为施加在材料上的力，A为作用力的垂直面积，δL为力作用时材料的伸长或压缩量，L0为材料的原始长度。

杨氏模量的数值越大，说明材料越难以被拉伸或压缩，具有更好的刚性。

而数值较小的材料则较容易被拉伸或压缩，具有较强的弹性。

杨氏模量的数值受多种因素影响，主要包括材料的组成、晶体结构、缺陷和温度等。

材料的组成和晶体结构决定了材料的弹性性质，不同的材料具有不同的杨氏模量；而材料内部的缺陷会导致应力集中，减小材料的杨氏模量。

此外，温度也会对杨氏模量产生影响，高温下材料的热膨胀会增加杨氏模量。

杨氏模量的应用非常广泛，特别是在工程领域。

例如，在建筑设计中，设计师需要了解材料的杨氏模量，以确定材料在各种应力下的变形情况，从而设计出更安全和稳定的结构。

在机械工程中，杨氏模量可以用来计算材料的刚度，评估材料是否适用于特定的应用。

此外，杨氏模量还可以用来衡量材料的硬度。

一般来说，杨氏模量较大的材料通常具有较高的硬度。

硬度可以用来评估材料的抗刮擦能力和耐磨性，对于一些需要经受摩擦或冲击的应用非常重要。

因此，在材料选择和工程设计中，了解材料的杨氏模量对于提供合适的材料解决方案至关重要。

总之，杨氏模量是描述材料弹性特性的重要参数，可以用来衡量材料的刚性、弹性和硬度等特性。

杨氏模量实验报告实验目的：通过实验测量材料的杨氏模量，了解材料的力学性质。

实验原理：杨氏模量是衡量材料刚性的一个重要指标，表示单位面积受力时，材料相对于长度的伸缩变形。

杨氏模量的计算公式为：E = F/A*dL/L0，其中E为杨氏模量，F为受力，A为受力面积，dL为长度变化量，L0为初始长度。

实验装置：1. 杨氏弹性模量测定装置：包括一个弹簧体、两个支架、一个测量刻度盘等。

2. 悬挂杆：用于悬挂弹簧体。

3. 质量盘：通过增加质量的方式给弹簧体施加力。

4. 测量仪器：包括测量尺、游标卡尺等。

实验步骤：1. 将杨氏弹性模量测定装置垂直固定在水平工作台上，并调整支架和弹簧体的位置，使其水平放置。

2. 使用尺子测量出杨氏弹性模量测定装置的长度L0，并记录下来。

3. 将质量盘挂在弹簧体上，并使用测量尺测量出弹簧体的长度变化量dL，记录下来。

4. 根据实验装置的参数和测量数据，计算出杨氏模量E。

实验数据处理：1. 计算杨氏模量的公式为E = F/A*dL/L0。

2. 假设弹簧体的截面积为A，施加的力为F，则可以根据施加的力和质量盘的质量计算出A和F的值。

3. 将A和F的值代入计算公式，得到杨氏模量的数值。

实验结果：根据实验数据和计算公式，得到杨氏模量的数值。

实验讨论：1. 实验测量中可能存在的误差，如弹簧体的形变、测量尺的误差等，需要进行分析和讨论。

2. 如何提高实验测量的准确性和精度，可以探讨使用更精确的测量仪器、改进实验装置设计等方法。

结论：根据实验测量数据和计算结果，得到杨氏模量的数值，并进行讨论和分析，从而对材料的力学性质有一定的了解。