系统可靠性理论与威布尔分布
- 格式:ppt
- 大小:921.81 KB
- 文档页数:51


可靠性理论基础知识可靠性理论基础知识1.可靠性定义我国军用标准GIB 451A-2005《可靠性维修性保障性术语》中,可靠性定义为:产品在规定的条件下,规定的时间内,完成规定功能的能力。
“规定条件”包括使用时的环境条件和工作条件。
“规定时间”是指产品规定了的任务时间。
“规定功能”是指产品规定了的必须具备的功能及其技术指标。
可靠性的评价可以使用概率指标或时间指标,这些指标有:可靠度、失效率、平均无故障工作时间、平均失效前时间、有效度等。
典型的失效率曲线是浴盆曲线,其分为三个阶段:早期失效期、偶然失效期、耗损失效期。
早期失效期的失效率为递减形式,即新产品失效率很高,但经过磨合期,失效率会迅速下降。
偶然失效期的失效率为一个平稳值,意味着产品进入了一个稳定的使用期。
耗损失效期的失效率为递增形式,即产品进入老年期,失效率呈递增状态,产品需要更新。
1.1可靠性参数1、失效概率密度和失效分布函数失效分布函数就是寿命的分布函数,也称为不可靠度,记为)(t F 。
它是产品或系统在规定的条件下和规定的时间内失效的概率,通常表示为)()(t T P t F ≤=失效概率密度是累积失效概率对时间t 的倒数,记为f(t)。
它是产品在包含t 的单位时间内发生失效的概率,可表示为)()()('t F dtt dF t f ==。
2、可靠度可靠度是指产品或系统在规定的条件下,规定的时间内,完成规定功能的概率。
可靠度是时间的函数,可靠度是可靠性的定量指标。
可靠度是时间的函数,记为)(t R 。
通常表示为?∞=-=>=t dt t f t F t T P t R )()(1)()(式中t 为规定的时间,T 表示产品寿命。
3、失效率已工作到时刻t 的产品,在时刻t 后单位时间内发生失效的概率成为该产品时刻t 的失效率函数,简称失效率,记为)(t λ。
)(1)()()()()()(''t F t F t R t F t R t f t -===λ。

威布尔分布的可靠性应用我们谈可靠性,往往离不开开篇大幅统计学介绍。
很多可靠性参考书,第一章也都是失效模型、可靠度函数、失效率函数、MTBF等。
不吹不尬,可靠性确实离不开概率统计。
比如我们了解到很多实验设计中的数量选择都不是凭空虚设,也并非经验论的拍脑袋,大多都是依据失效函数、置信度等进行计算;再如我们预设的产品寿命是通过加速实验推算的数值,如果某家公司真的执行了诚意满满的寿命估算,估计做一批数量的样品,保证十年的使用寿命,客户和市场也该等的花都谢了;又如我们建立的很多数学模型都不可能完全印证实际情况,当丰满理想遭遇骨感现实,概率就可以跳出来为你不敢做保票的那一步找个台阶下。
图中是常用的可靠性分布及其对应的应用场景,主要分为离散和连续分布。
可靠性常用概率分布今天我们主要聊聊Weibull分布,也就是图中故意卖关子的这一项。
威布尔分布表达式异常复杂,在可靠性中使用范围却很广。
其中失效密度函数表示如下:m: 形状参数,表示函数的走势,m>1,表示失效率随时间增加,m<1, 表示失效率随时间减小。
t0: 参数或特征寿命,表示函数的缩放。
γ :位置参数,且γ >0; 表示设备在[0, γ ]之间不会发生故障。
威布尔分布之所以好用,是因为通过调整不同参数,可以表征整个产品生命周期,即可靠性常提到的浴盆曲线,分为早期失效、随机失效和老化失效三个阶段。
早期失效,产品在开始使用时,失效率很高,但随着产品工作时间的增加,失效率迅速降低。
这一阶段失效的原因大多是由于设计、原材料和制造过程中的缺陷造成的。
随机失效期,是失效率较低,且较稳定,往往可近似看作常数,可以用指数分布表示。
这一时期是产品的良好使用阶段, 偶然失效主要原因是质量缺陷、材料弱点、环境和使用不当。
老化阶段,失效率随时间的延长而急速增加, 主要由磨损、疲劳、老化和耗损等原因造成。
这个阶段也可以用正态分布来做模拟。
Weibull分布参数与失效模型之间的关系:假设给我们一组数据,是实验中给定时间段内的失效样品数量统计,将这组数据在minitab中做直方图,我们可以大概感觉这组数据是处于产品的早期失效阶段,用分布进行拟合,如下分别用威布尔三参分布、双参指数分布、三参数对数正态分布、三参数伽玛分布都可以来表示这组数据的分布。
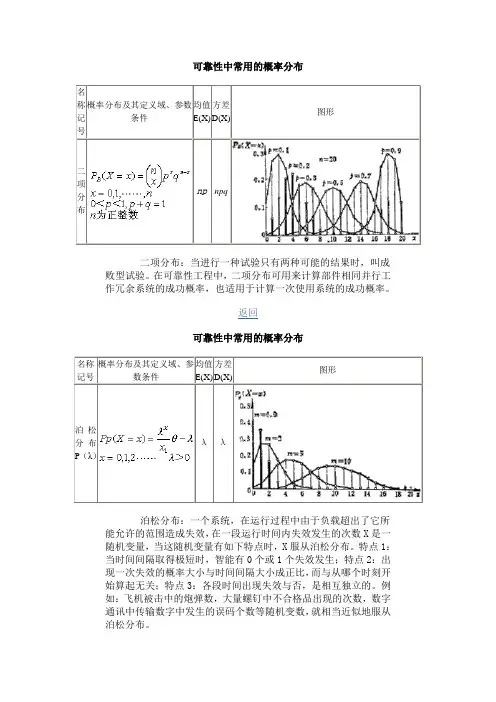
名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形二项分布np npq二项分布:当进行一种试验只有两种可能的结果时,叫成败型试验。
在可靠性工程中,二项分布可用来计算部件相同并行工作冗余系统的成功概率,也适用于计算一次使用系统的成功概率。
返回可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形泊松分布P(λ)λλ泊松分布:一个系统,在运行过程中由于负载超出了它所能允许的范围造成失效,在一段运行时间内失效发生的次数X是一随机变量,当这随机变量有如下特点时,X服从泊松分布。
特点1:当时间间隔取得极短时,智能有0个或1个失效发生;特点2:出现一次失效的概率大小与时间间隔大小成正比,而与从哪个时刻开始算起无关;特点3:各段时间出现失效与否,是相互独立的。
例如:飞机被击中的炮弹数,大量螺钉中不合格品出现的次数,数字通讯中传输数字中发生的误码个数等随机变数,就相当近似地服从泊松分布。
名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形超几何分布H(n,M,N)返回可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形指数分布e(λ)指数分布:许多电子产品的寿命分布一般服从指数分布。
有的系统的寿命分布也可用指数分布来近似。
它在可靠性研究中是最常用的一种分布形式。
指数分布是伽玛分布和威布尔分布的特殊情况,产品的失效是偶然失效时,其寿命服从指数分布。
可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形威布尔分布(Ⅲ型极值分布)W(k,a,b)威布尔分布:在可靠性工程中被广泛应用,尤其适用于机电类产品的磨损累计失效的分布形式。
由于它可以利用概率纸很容易地推断出它的分布参数,被广泛应用与各种寿命试验的数据处理。
可靠性中常用的概率分布名称记号概率分布及其定义域、参数条件均值E(X)方差D(X)图形正态分布(高斯分布)N(μ,σ)μσ2正态分布:是在机械产品和结构工程中,研究应力分布和强度分布时,最常用的一种分布形式。


威布尔概率分布及应用威布尔概率分布是一种常用的统计分布模型,适用于描述正向偏斜的连续随机变量的概率分布。
在工程学中,威布尔分布经常用来模拟和分析可靠性和寿命数据。
下面将详细介绍威布尔概率分布及其应用。
1. 威布尔概率分布的定义与特性:威布尔概率密度函数的表达式为:f(x) = (a/b)((x/b)^(a-1)) * exp(-(x/b)^a)其中,a和b均为正实数,是概率分布的参数。
该概率密度函数主要用来描述随机变量X的寿命分布。
威布尔分布的累积分布函数为:F(x) = 1 - exp(-(x/b)^a)威布尔分布具有如下特性:(1) 当a=1时,威布尔分布退化为指数分布。
(2) 当a>1时,威布尔分布具有右偏斜的特性。
(3) 威布尔分布的均值为b * Γ(1 + 1/a),其中Γ表示伽玛函数。
(4) 威布尔分布的方差为b^2 * (Γ(1 + 2/a) - (Γ(1 + 1/a))^2)。
2. 威布尔概率分布的应用:(1) 可靠性分析:威布尔分布常用于可靠性分析中,可以通过威布尔分布来描述产品的寿命分布。
通过分析得到的威布尔分布,可以计算产品在某个时间点的可靠性,确定其在给定时间段内的失效概率,并进一步寻找改进措施,提高产品的可靠性。
(2) 寿命数据分析:威布尔分布也广泛应用于对某些机械设备、材料或系统的寿命数据进行建模与分析。
通过对实际寿命数据进行威布尔分布拟合,可以更准确地预测设备或系统在未来某个时间段内的失效概率,帮助制定相应的维修和更换计划。
(3) 临床试验:在医学和生物学中,临床试验数据经常具有右偏性,且描述的是某种事件或现象的寿命。
因此,威布尔分布在临床试验数据分析中的应用十分常见。
通过拟合试验数据得到的威布尔分布可以为研究人员提供反映疾病发展或治疗效果的信息,从而指导临床实践和决策。
(4) 金融风险管理:在金融领域,威布尔分布可以用来对风险事件的发生概率进行建模,如市场波动、信用违约等。

可靠性可靠性函数函数函数与与Weibull 分布Xie Meng-xian. (电子科大,成都市)半导体器件和集成电路的可靠性评估(即失效率预测,failure rate prediction )是一个重要的问题。
可靠性评估实际上也就是采用通过寿命试验而得到的失效的数据、来估算出器件和集成电路的有效使用寿命。
有效使用寿命即为器件和集成电路能够正常工作的平均平均平均使用使用使用时间时间(MTTF ,mean time to failure );与此密切相关的概念是失效率失效率失效率(或故障率,failure rate ),即单位时间内所失效的器件和电路的数目,常用的单位是FIT (10−9/小时)或者%/1000小时。
因为通过寿命试验而获得的失效数据,往往遵从某种规律的分布函数——可靠性函数,所以根据这些试验数据,由可靠性函数规律出发,即可估算出器件和集成电路的MTTF 和失效率。
(1)可靠性函数:半导体器件和集成电路会由于各种原因而失效,但是失效率往往与使用时间有关。
若在经过时间t 之后未失效器件的数目为R(t),则通过寿命试验可以获得大致如图1所示的三种模式的函数关系:①早期失效模式;②偶发失效模式;③磨损失效模式。
在数学上可用来描述这些失效模式的函数即称为可靠性函数。
对于偶发失效的模式,比较符合实际的可靠性函数是指数函数;由此可知偶发失效的失效率是一个常数,即不管经过多长时间,器件失效的几率都是一样的;根据这种可靠性函数,可较容易地进行分析。
比偶发失效更早发生的失效称为早期失效。
大多数半导体器件和集成电路所出现的失效都属于早期失效模式。
对于这种很快就会发生失效的器件和电路,一般都可以在使用之前、通过例行试验(即采用一定条件的筛选工艺)来去除掉,以免带来后患。
磨损失效也称为疲劳失效,其特点是开始阶段的故障少,然后故障不断增加。
(2)Weibull 分布:从统计角度来看,统计数据的分布函数有许多种,常用的有如指数分布、Gauss 分布、Γ分布、对数正态分布和Weibull 分布,它们的功能各有千秋。

威布尔分布下复杂系统可靠性与全寿命周期费用综合建模一、开篇随着社会的发展,人们对产品和服务的质量和可靠性的要求越来越高。
而在现代经济中,复杂系统可靠性和全寿命周期成本是一项重要的经济指标。
在对于复杂系统的可靠性建模方面,威布尔分布是一种被广泛应用的概率分布,能够很好地描述产品或系统的寿命分布特性。
本文将围绕威布尔分布下的复杂系统可靠性与全寿命周期费用综合建模进行探讨,提出五个主题,包括:威布尔分布概述、威布尔分布建模、复杂系统可靠性建模、全寿命周期费用建模以及综合建模分析。
二、威布尔分布概述威布尔分布是一种常见的概率分布,被广泛应用于描述复杂系统的寿命分布特征。
其密度函数为:$$f(t) = \frac{\gamma}{\beta}(\frac{t-\mu}{\beta})^{\gamma-1}e^{-(\frac{t-\mu}{\beta})^\gamma}$$其中,$\mu$ 是位置参数,$\beta$ 是尺度参数, $\gamma$ 是形状参数。
在描述复杂系统的可靠性时,通常使用的是威布尔分布的累积分布函数:$$F(t) = 1 - e^{-(\frac{t-\mu}{\beta})^\gamma}$$这个函数能够描述系统在经过 $t$ 时间后仍然正常运行的概率。
三、威布尔分布建模在实际应用中,可以通过对系统的寿命数据进行威布尔分布拟合,来推断出系统的寿命特征。
比如,对于某一型号的产品,可以通过测量若干台设备的使用寿命,然后进行威布尔分布拟合,得到该型号设备的寿命分布特性。
从而可以预测出未来产品或系统的使用寿命,为制定产品或系统的维修计划和调整资产管理策略提供依据。
四、复杂系统可靠性建模复杂系统可靠性建模是指根据系统的失效信息,利用可靠性理论、统计学和计算机技术等技术手段,对系统的失效概率、失效时间、失效原因等进行分析和预测,以提高系统的运行可靠性。
威布尔分布可以用于对复杂系统的失效时间进行建模。



关于威布尔分布在可靠性分析应用中的几个问题
第一章:绪论
威布尔分布是可靠性分析领域中常用的概率分布模型之一。
本文通过对威布尔分布的概念、特点和应用进行分析,探讨威布尔分布在可靠性分析中的应用问题,以期提高可靠性分析的精度和准确性。
第二章:威布尔分布的概念及特点
威布尔分布是一种用于描述时间或次数随机变量的概率分布。
其特点在于具有相对稳定的失效率,即随着时间的推移,失效率单调递增,这种特点使得威布尔分布在可靠性分析中得到广泛应用。
文中详细阐述威布尔分布的数学模型,以及其在可靠性分析中的应用范围和限制。
第三章:威布尔分布作为失效模型的应用
威布尔分布可以作为失效模型来描述事物的失效规律。
在可靠性分析中,威布尔分布常用于分析和预测产品的寿命及其失效的概率。
本章介绍了该分布模型在可靠性分析中的应用,并提出了利用该分布模型进行可靠性设计的一些方法和思路。
第四章:威布尔分布在可靠性评估中的应用问题
威布尔分布通常作为失效模型或寿命分布模型来应用于可靠性评估中。
本章主要探讨了采用威布尔分布进行可靠性评估时可能遇到的问题,如威布尔分布参数的估计、威布尔分布模型的拟合优度评价等。
同时,本章还对这些问题进行了一些探讨和解决的方法。
第五章:结论
综上所述,威布尔分布作为可靠性分析的一种重要工具,在可靠性设计、失效分析和可靠性评估等领域的应用范围都非常广泛。
但是,在使用威布尔分布进行可靠性分析时,也需要注意该分布模型的局限性及其在使用中可能遇到的问题,同时还需要深入研究和探讨威布尔分布模型的其他应用领域。
《可靠性工程技术》课程复习重点一、掌握以下知识点:1.可靠性:产品在规定的条件下和规定的时间内完成规定功能的能力。
也就是说,产品是否可靠,取决于这样一个试验结果,即产品在规定的条件下和规定的时间内是否完成了规定功能。
2.随机事件1.如果所进行的科学试验具有以下特点,那么,我们称这种试验为随机试验,简称试验。
①可以在相同的条件下重复进行。
②每个试验的可能结果不止一个,并且能事先预测试验的所有可能结果。
③进行一次试验之前不能确定哪一个结果会出现。
3.威布尔分布的定义:威布尔分布在可靠性理论中是适用范围较广的一种分布。
它能全面地描述浴盆失效概率曲线的各个阶段。
当威布尔分布中的参数不同时,它可以蜕化为指数分布、瑞利分布和正态分布。
大量实践说明,凡是因为某一局部失效或故障所引起的全局机能停止运行的元件、器件、设备、系统等的寿命服从威布尔分布,特别在研究金属材料的疲劳寿命(如疲劳失效、轴承失效)都服从威布尔分布。
4. 事件把随机试验的任何一个可能发生的结果称为随机事件,简称事件5.均匀分布均匀分布又称等可能分布,即在随机变量可能取值范围内,其概率密度值是相等的,失效概率密度函数是一段等高线,是常量。
6.指数分布指数分布在可靠性理论中,指数分布是最基本、最常用的分布,适合于失效率λ( t )为常数的情况,它不但在电子元器件偶然失效期普遍使用,而且在复杂系统和整机方面以及机械技术的可靠性领域也得到使用。
7.可靠度可靠度是产品在寿命周期内完成规定功能的指标。
按我国国标规定,可靠度的定义是“在规定的条件下,在规定的时间内完成规定功能的概率”,即产品在规定的条件下,规定的时间内的可靠性。
时间越长,可靠性越低,时间越短,可靠性越高,时间为零时,可靠性最高,即为 l ,因此可靠性是时间的函数,用 R 表示可靠性,则 R ( t )为可靠性函数,即可靠度。
8.可靠性框图可靠性框图是将产品(系统)的结构功能按着可靠性要求进行分析的表示方法,该框图能清晰准确地描述产品(系统)的各元器件间的可靠性关系与功能。
南开大学硕士学位论文威布尔分布参数估计的研究姓名:赵呈建申请学位级别:硕士专业:概率论与数理统计指导教师:张润楚20071101威布尔分布参数估计的研究作者:赵呈建学位授予单位:南开大学本文读者也读过(10条)1.朱铭扬.ZHU Ming-yang三参数威布尔分布的参数估计[期刊论文]-江苏技术师范学院学报2006,12(6)2.赵冰锋.吴素君三参数威布尔分布参数估计方法[会议论文]-20073.赵冰锋.吴素君三参数威布尔分布参数估计方法[会议论文]-20074.史景钊.杨星钊.陈新昌.SHI Jing-zhao.YANG Xing-zhao.CHEN Xin-chang3参数威布尔分布参数估计方法的比较研究[期刊论文]-河南农业大学学报2009,43(4)5.张慧敏.ZHANG Hui-min三参数威布尔分布在机械可靠性分析中的应用[期刊论文]-机械管理开发2009,24(3)6.郑荣跃.严剑松威布尔分布参数估计新方法研究[期刊论文]-机械强度2002,24(4)7.杨志忠.刘瑞元三参数Weibull分布参数估计求法改进[期刊论文]-工程数学学报2004,21(2)8.邢兆飞威布尔分布可靠度的近似置信限和浴盆形失效率函数及其统计分析[学位论文]20099.赵冰锋.吴素君.ZHAO Bing-feng.WU Su-jun三参数威布尔分布参数估计方法[期刊论文]-金属热处理2007,32(z1)10.严晓东.马翔.郑荣跃.吴亮.YAN Xiao-dong.MA Xiang.ZHENG Rong-yue.WU Liang三参数威布尔分布参数估计方法比较[期刊论文]-宁波大学学报(理工版)2005,18(3)引用本文格式:赵呈建威布尔分布参数估计的研究[学位论文]硕士 2007。
可靠性设计与分析作业学号:071130123 姓名:向正平一、指数分布的概率密度函数、分布函数、可靠度函数曲线(1)程序语言t=(0:0.01:20); Array m=[0.3,0.6,0.9];linecolor=['r','b','y'];for i=1:length(m);f=m(i)*exp(-m(i)*t);F=1-exp(-m(i)*t);R=exp(-m(i)*t);color=linecolor(i);subplot(3,1,1);title('指数函数概率密度函数曲线');plot(t,f,color);hold onsubplot(3,1,2);title('指数函数分布函数函数曲线');plot(t,F,color);hold onsubplot(3,1,3);title('指数指数分布可靠度函数曲线plot(t,R,color);hold onend(3)指数分布的分析在可靠性理论中,指数分布是最基本、最常用的分布,适合于失效率为常数的情况。
指数分布不但在电子元器件偶然失效期普遍使用,而且在复杂系统和整机方面以及机械技术的可靠性领域也得到使用。
有图像可以看出失效率函数密度f(t)随着时间的增加不断下降,而失效率随着时间的增加在不断的上升,可靠度也在随着时间的增加不断地下降,从图线的颜色可以看出,随着m的增加失效率密度函数下降越快,而可靠度的随m的增加而不断的增加,则失效率随m的增加减小越快。
在工程运用中,如果某零件符合指数分布,那么可以适当增加m的值,使零件的可靠度会提升,增加可靠性。
二、正态分布的概率密度函数、分布函数、可靠性函数、失效率函数曲线(1)程序语言t=-10:0.01:10;m=[3,6,9];n=[1,2,3];linecolor=['r','b','y'];for i=1:length(m);f=1./(sqrt(2*3.14).*m(i)).*exp(-(t-n(i)).^2./(2*m(i).^2)); F=cumtrapz(t,f);R=1-F;Lamenda=(2.*3.14).^(-1./2)/m(i).*exp(-(t-n(i)).^2/(2.*m(i).^2))./(2*3.14).^(-1./2)./m(i).*cumtrapz(t,exp(-(t-n(i)).^2./(2.*m(i).^2)));color=linecolor(i);subplot(2,2,1);title('正态分布概率密度函数');plot(t,f,color);hold onsubplot(2,2,2);title('正态分布分布函数');plot(t,F,color);hold onsubplot(2,2,3);title('正态分布可靠度函数');plot(t,R,color);hold onsubplot(2,2,4);title('正态分布失效率函数');plot(t,Lamenda,color);hold onend(3)正态分布的分析正态分布在数理统计学中是一个最基本的分布,在可靠性技术中也经常用到它,如材料强度、磨损寿命、疲劳失效、同一批晶体管放大倍数的波动或寿命波动等等都可看作或近似看作正态分布。