第七章面理讲义和线理

§7.3 基本不等式及其应用最新考纲 1.探索并了解基本不等式的证明过程.2.会用基本不等式解决简单的最大(小)值问题．1．基本不等式：ab ≤a ＋b 2(1)基本不等式成立的条件：a >0，b >0.(2)等号成立的条件：当且仅当a ＝b 时取等号． 2．几个重要的不等式 (1)a 2＋b 2≥2ab (a ，b ∈R )． (2)b a ＋ab ≥2(a ，b 同号)． (3)ab ≤⎝⎛⎭⎫a ＋b 22(a ，b ∈R )．(4)a 2＋b 22≥⎝⎛⎫a ＋b 22 (a ，b ∈R )． 以上不等式等号成立的条件均为a ＝b . 3．算术平均数与几何平均数设a >0，b >0，则a ，b 的算术平均数为a ＋b 2，几何平均数为ab ，基本不等式可叙述为两个正数的算术平均数不小于它们的几何平均数． 4．利用基本不等式求最值问题 已知x >0，y >0，则(1)如果积xy 是定值p ，那么当且仅当x ＝y 时，x ＋y 有最小值2p .(简记：积定和最小) (2)如果和x ＋y 是定值p ，那么当且仅当x ＝y 时，xy 有最大值p 24.(简记：和定积最大)概念方法微思考1．若两个正数的和为定值，则这两个正数的积一定有最大值吗？提示 不一定．若这两个正数能相等，则这两个数的积一定有最大值；若这两个正数不相等，则这两个正数的积无最大值．2．函数y ＝x ＋1x的最小值是2吗？提示 不是．因为函数y ＝x ＋1x 的定义域是{x |x ≠0}，当x <0时，y <0，所以函数y ＝x ＋1x 无最小值．题组一 思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”) (1)函数f (x )＝cos x ＋4cos x，x ∈⎝⎛⎭⎫0，π2的最小值等于4.( × ) (2)“x >0且y >0”是“x y ＋yx ≥2”的充要条件．( × )(3)(a ＋b )2≥4ab (a ，b ∈R )．( √ )(4)若a >0，则a 3＋1a2的最小值为2a .( × )(5)不等式a 2＋b 2≥2ab 与a ＋b2≥ab 有相同的成立条件．( × )(6)两个正数的等差中项不小于它们的等比中项．( √ ) 题组二 教材改编2．设x >0，y >0，且x ＋y ＝18，则xy 的最大值为( ) A ．80 B ．77 C ．81 D ．82 答案 C解析 ∵x >0，y >0，∴x ＋y2≥xy ，即xy ≤⎝⎛⎭⎫x ＋y 22＝81，当且仅当x ＝y ＝9时，(xy )max ＝81.3．若把总长为20 m 的篱笆围成一个矩形场地，则矩形场地的最大面积是________ m 2. 答案 25解析 设矩形的一边为x m ，面积为y m 2， 则另一边为12×(20－2x )＝(10－x )m ，其中0<x <10，∴y ＝x (10－x )≤⎣⎡⎦⎤x ＋(10－x )22＝25，当且仅当x ＝10－x ，即x ＝5时，y max ＝25. 题组三 易错自纠4．“x >0”是“x ＋1x ≥2成立”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案 C解析 当x >0时，x ＋1x≥2x ·1x＝2. 因为x ，1x 同号，所以若x ＋1x ≥2，则x >0，1x >0，所以“x >0”是“x ＋1x ≥2成立”的充要条件，故选C.5．若函数f (x )＝x ＋1x －2(x >2)在x ＝a 处取最小值，则a 等于( )A ．1＋ 2B ．1＋ 3C ．3D ．4 答案 C解析 当x >2时，x －2>0，f (x )＝(x －2)＋1x －2＋2≥2(x －2)×1x －2＋2＝4，当且仅当x －2＝1x －2(x >2)，即x ＝3时取等号，即当f (x )取得最小值时，x ＝3，即a ＝3，故选C. 6．若正数x ，y 满足3x ＋y ＝5xy ，则4x ＋3y 的最小值是( ) A ．2 B ．3 C ．4 D ．5 答案 D解析 由3x ＋y ＝5xy ，得3x ＋y xy ＝3y ＋1x ＝5，所以4x ＋3y ＝(4x ＋3y )·15⎝⎛⎭⎫3y ＋1x ＝15⎝⎛⎭⎫4＋9＋3y x ＋12x y ≥15(4＋9＋236)＝5， 当且仅当3y x ＝12xy ，即y ＝2x 时，“＝”成立，故4x ＋3y 的最小值为5.故选D.题型一 利用基本不等式求最值 命题点1 配凑法例1 (1)已知0<x <1，则x (4－3x )取得最大值时x 的值为________． 答案 23解析 x (4－3x )＝13·(3x )(4－3x )≤13·⎣⎡⎦⎤3x ＋(4－3x )22＝43， 当且仅当3x ＝4－3x ，即x ＝23时，取等号．(2)函数y ＝x 2＋2x －1(x >1)的最小值为________．答案 23＋2解析 ∵x >1，∴x －1>0，∴y ＝x 2＋2x －1＝(x 2－2x ＋1)＋(2x －2)＋3x －1＝(x －1)2＋2(x －1)＋3x －1＝(x －1)＋3x －1＋2≥23＋2.当且仅当x －1＝3x －1，即x ＝3＋1时，等号成立．命题点2 常数代换法例2 (2019·大连模拟)已知首项与公比相等的等比数列{a n }中，满足a m a 2n ＝a 24(m ，n ∈N *)，则2m ＋1n的最小值为( ) A ．1 B.32 C ．2 D.92答案 A解析 由题意可得，a 1＝q ，∵a m a 2n ＝a 24，∴a 1·q m －1·(a 1·q n －1)2＝(a 1·q 3)2，即q m ·q 2n ＝q 8， 即m ＋2n ＝8.∴2m ＋1n＝(m ＋2n )⎝⎛⎭⎫2m ＋1n ×18 ＝⎝⎛⎭⎫2＋m n ＋4n m ＋2×18≥()4＋24×18＝1. 当且仅当m ＝2n 时，即m ＝4，n ＝2时，等号成立． 命题点3 消元法例3 已知正实数a ，b 满足a 2－b ＋4≤0，则u ＝2a ＋3b a ＋b ( )A ．有最大值145B ．有最小值145C ．有最小值3D ．有最大值3答案 B解析 ∵a 2－b ＋4≤0，∴b ≥a 2＋4， ∴a ＋b ≥a 2＋a ＋4.又∵a ，b >0，∴a a ＋b ≤aa 2＋a ＋4，∴－a a ＋b ≥－a a 2＋a ＋4，∴u ＝2a ＋3b a ＋b ＝3－a a ＋b ≥3－a a 2＋a ＋4＝3－1a ＋4a＋1≥3－12a ·4a ＋1＝145， 当且仅当a ＝2，b ＝8时取等号．故选B.思维升华 (1)前提：“一正”“二定”“三相等”．(2)要根据式子的特征灵活变形，配凑出积、和为常数的形式，然后再利用基本不等式． (3)条件最值的求解通常有三种方法：一是消元法；二是将条件灵活变形，利用常数“1”代换的方法；三是配凑法．跟踪训练1 (1)(2019·四平质检)设x >0，y >0，若x lg 2，lg 2，y lg 2成等差数列，则1x ＋9y 的最小值为( )A ．8B ．9C ．12D ．16 答案 D解析 ∵x lg 2，lg 2，y lg 2成等差数列， ∴2lg 2＝(x ＋y )lg 2，∴x ＋y ＝1. ∴1x ＋9y＝(x ＋y )⎝⎛⎭⎫1x ＋9y ≥10＋2y x ·9xy＝10＋6＝16， 当且仅当x ＝14，y ＝34时取等号，故1x ＋9y的最小值为16.故选D. (2)若a ，b ，c 都是正数，且a ＋b ＋c ＝2，则4a ＋1＋1b ＋c 的最小值是( )A ．2B ．3C ．4D ．6 答案 B解析 ∵a ，b ，c 都是正数，且a ＋b ＋c ＝2， ∴a ＋b ＋c ＋1＝3， 且a ＋1>0，b ＋c >0.∴4a ＋1＋1b ＋c ＝13·(a ＋1＋b ＋c )·⎝⎛⎭⎫4a ＋1＋1b ＋c ＝13⎣⎢⎡⎦⎥⎤5＋4(b ＋c )a ＋1＋a ＋1b ＋c ≥13(5＋4)＝3.当且仅当a ＋1＝2(b ＋c )，即a ＝1，b ＋c ＝1时，等号成立．故选B. 题型二 基本不等式的综合应用命题点1 基本不等式与其他知识交汇的最值问题例4 (2018·重庆诊断)已知圆O 的方程为x 2＋y 2＝1，过第一象限内圆O 外的点P (a ，b )作圆O 的两条切线P A ，PB ，切点分别为A ，B ，若PO →·P A →＝8，则a ＋b 的最大值为( ) A ．3 B ．3 2 C ．4 2 D ．6答案 B解析 根据题意，结合向量数量积的定义式， 可求得PO →·P A →＝|P A →|2＝8，所以可求得|PO |2＝9， 即a 2＋b 2＝9，结合基本不等式， 可得a ＋b ≤2(a 2＋b 2)＝32， 当且仅当a ＝b ＝322时取等号，故选B.命题点2 求参数值或取值范围例5 (2018·中山模拟)已知不等式(x ＋y )⎝⎛⎭⎫1x ＋a y ≥9对任意正实数x ，y 恒成立，则正实数a 的最小值为( ) A ．2 B ．4 C ．6 D ．8 答案 B解析 已知不等式(x ＋y )⎝⎛⎭⎫1x ＋a y ≥9对任意正实数x ，y 恒成立，只要求(x ＋y )⎝⎛⎭⎫1x ＋a y 的最小值大于或等于9，∵1＋a ＋y x ＋axy ≥a ＋2a ＋1，当且仅当y ＝ax 时，等号成立， ∴a ＋2a ＋1≥9，∴a ≥2或a ≤－4(舍去)，∴a ≥4， 即正实数a 的最小值为4，故选B.思维升华 求参数的值或范围：观察题目特点，利用基本不等式确定相关成立条件，从而得参数的值或范围．跟踪训练2 (1)在△ABC 中，A ＝π6，△ABC 的面积为2，则2sin C sin C ＋2sin B ＋sin Bsin C 的最小值为( ) A.32B.334C.32D.53答案 C解析 由△ABC 的面积为2，所以S ＝12bc sin A ＝12bc sin π6＝2，得bc ＝8，在△ABC 中，由正弦定理得 2sin C sin C ＋2sin B ＋sin B sin C ＝2c c ＋2b ＋bc＝2cb b (c ＋2b )＋b 2bc＝168＋2b 2＋b 28＝84＋b 2＋b 2＋48－12≥284＋b2·b 2＋48－12＝2－12＝32， 当且仅当b ＝2，c ＝4时，等号成立，故选C.(2)已知函数f (x )＝ax 2＋bx (a >0，b >0)的图象在点(1，f (1))处的切线的斜率为2，则8a ＋bab的最小值是( ) A ．10 B ．9 C ．8 D ．3 2答案 B解析 由函数f (x )＝ax 2＋bx ，得f ′(x )＝2ax ＋b ， 由函数f (x )的图象在点(1，f (1))处的切线斜率为2， 所以f ′(1)＝2a ＋b ＝2，所以8a ＋b ab ＝1a ＋8b ＝12⎝⎛⎭⎫1a ＋8b (2a ＋b )＝12⎝⎛⎭⎫10＋b a ＋16a b ≥12⎝⎛⎭⎫10＋2b a ·16a b ＝12(10＋8)＝9，当且仅当b a ＝16a b ，即a ＝13，b ＝43时等号成立，所以8a ＋bab的最小值为9，故选B.利用基本不等式求解实际问题数学建模是对现实问题进行数学抽象，用数学的语言表达问题，用数学的方法构建模型解决问题．过程主要包括：在实际情景中从数学的视角发现问题、提出问题、分析问题、建立模型、确定参数、计算求解、检验结果、改进模型，最终解决实际问题．例 某厂家拟在2019年举行促销活动，经调查测算，该产品的年销售量(即该厂的年产量)x 万件与年促销费用m 万元(m ≥0)满足x ＝3－k m ＋1(k 为常数)，如果不搞促销活动，则该产品的年销售量只能是1万件．已知2019年生产该产品的固定投入为8万元．每生产1万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)．(1)将2019年该产品的利润y 万元表示为年促销费用m 万元的函数； (2)该厂家2019年的促销费用投入多少万元时，厂家的利润最大？ 解 (1)由题意知，当m ＝0时，x ＝1， ∴1＝3－k ⇒k ＝2， ∴x ＝3－2m ＋1，每万件产品的销售价格为1.5×8＋16xx (万元)，∴2019年的利润y ＝1.5x ×8＋16xx －8－16x －m＝4＋8x －m ＝4＋8⎝⎛⎭⎫3－2m ＋1－m＝－⎣⎡⎦⎤16m ＋1＋(m ＋1)＋29(m ≥0)．(2)∵m ≥0时，16m ＋1＋(m ＋1)≥216＝8， ∴y ≤－8＋29＝21，当且仅当16m ＋1＝m ＋1⇒m ＝3(万元)时，y max ＝21(万元)．故该厂家2019年的促销费用投入3万元时，厂家的利润最大为21万元．素养提升 利用基本不等式求解实际问题时根据实际问题抽象出目标函数的表达式，建立数学模型，再利用基本不等式求得函数的最值．1．函数f (x )＝x 2＋4|x |的最小值为( )A ．3B ．4C ．6D ．8答案 B解析 f (x )＝x 2＋4|x |＝|x |＋4|x |≥24＝4，当且仅当x ＝±2时，等号成立，故选B.2．若x >0，y >0，则“x ＋2y ＝22xy ”的一个充分不必要条件是( ) A ．x ＝y B ．x ＝2y C ．x ＝2且y ＝1 D ．x ＝y 或y ＝1 答案 C解析 ∵x >0，y >0，∴x ＋2y ≥22xy ，当且仅当x ＝2y 时取等号．故“x ＝2且y ＝1 ”是“x ＋2y ＝22xy ”的充分不必要条件．故选C. 3．(2018·潍坊模拟)已知正数a ，b 满足a ＋b ＝1，则4a ＋1b 的最小值为( )A.53 B ．3 C ．5 D ．9 答案 D解析 由题意知，正数a ，b 满足a ＋b ＝1， 则4a ＋1b ＝⎝⎛⎭⎫4a ＋1b (a ＋b ) ＝4＋1＋4b a ＋ab≥5＋24b a ·ab＝9， 当且仅当4b a ＝a b ，即a ＝23，b ＝13时等号成立，所以4a ＋1b的最小值为9，故选D.4．若a >0，b >0，lg a ＋lg b ＝lg(a ＋b )，则a ＋b 的最小值为( ) A ．8B ．6C ．4D ．2答案 C解析 由lg a ＋lg b ＝lg(a ＋b )，得lg(ab )＝lg(a ＋b )，即ab ＝a ＋b ，则有1a ＋1b ＝1，所以a ＋b＝⎝⎛⎭⎫1a ＋1b (a ＋b )＝2＋b a ＋ab ≥2＋2b a ·ab＝4，当且仅当a ＝b ＝2时等号成立，所以a ＋b 的最小值为4，故选C.5．已知函数f (x )＝e x 在点(0，f (0))处的切线为l ，动点(a ，b )在直线l 上，则2a ＋2－b的最小值是( ) A ．4 B ．2 C ．2 2 D. 2答案 D解析 由题意得f ′(x )＝e x ，f (0)＝e 0＝1，k ＝f ′(0)＝e 0＝1.所以切线方程为y －1＝x －0，即x －y ＋1＝0，∴a －b ＋1＝0，∴a －b ＝－1，∴2a ＋2－b ≥22a ·2－b ＝22a －b ＝22－1＝ 2⎝⎛⎭⎫当且仅当a ＝－12，b ＝12时取等号，故选D.6.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据，通过这一原理，很多的代数的公理或定理都能够通过图形实现证明，也称之为无字证明．现有如图所示图形，点F 在半圆O 上，点C 在直径AB 上，且OF ⊥AB ，设AC ＝a ，BC ＝b ，则该图形可以完成的无字证明为( )A.a ＋b2≥ab (a >0，b >0)B ．a 2＋b 2≥2ab (a >0，b >0) C.2ab a ＋b ≤ab (a >0，b >0) D.a ＋b 2≤a 2＋b 22(a >0，b >0) 答案 D解析 由AC ＝a ，BC ＝b ，可得圆O 的半径r ＝a ＋b2，又OC ＝OB －BC ＝a ＋b 2－b ＝a －b2，则FC 2＝OC 2＋OF 2＝(a －b )24＋(a ＋b )24＝a 2＋b 22，再根据题图知FO ≤FC ，即a ＋b 2≤ a 2＋b 22，当且仅当a ＝b 时取等号．故选D. 7．设x ，y 均为正数，且xy ＋x －y －10＝0，则x ＋y 的最小值是________．答案 6解析 由xy ＋x －y －10＝0，得x ＝y ＋10y ＋1＝9y ＋1＋1， ∴x ＋y ＝9y ＋1＋1＋y ≥29y ＋1·(1＋y )＝6， 当且仅当9y ＋1＝1＋y ，即y ＝2时，等号成立． 8．(2019·吉林梅河口二中模拟)设正项等比数列{a n }的前n 项和为S n ，若S 7－S 5＝3(a 4＋a 5)，则4a 3＋9a 7的最小值为________． 答案 4解析 设正项等比数列{a n }的公比为q (q >0)，∵S 7－S 5＝a 7＋a 6＝3(a 4＋a 5)，∴a 7＋a 6a 5＋a 4＝q 2＝3. ∴4a 3＋9a 7＝4a 3＋9a 3q 4＝4a 3＋1a 3≥24a 3·1a 3＝4， 当且仅当4a 3＝1a 3，即a 3＝12时等号成立． ∴4a 3＋9a 7的最小值为4. 9．(2018·肇庆模拟)已知△ABC 的角A ，B ，C 的对边分别为a ，b ，c ，若a 2＝b 2＋c 2－bc ，且△ABC 的面积为334，则a 的最小值为________． 答案 3解析 由题意得b 2＋c 2－a 2＝bc ，∴2bc cos A ＝bc ，∴cos A ＝12，∴A ＝π3. ∵△ABC 的面积为334， ∴12bc sin A ＝343，∴bc ＝3. ∵a 2＝b 2＋c 2－bc ，∴a 2≥2bc －bc ＝bc ＝3(当且仅当b ＝c 时，等号成立)，∴a ≥ 3.10．已知a ，b 为正实数，且(a －b )2＝4(ab )3，则1a ＋1b的最小值为________． 答案 2 2解析 由题意得(a －b )2＝(a ＋b )2－4ab ，代入已知得(a ＋b )2＝4(ab )3＋4ab ，两边同除以(ab )2得⎝⎛⎭⎫a ＋b ab 2＝4(ab )3a 2b 2＋4ab a 2b 2 ＝4⎝⎛⎭⎫ab ＋1ab ≥4·2ab ·1ab＝8， 当且仅当ab ＝1时取等号．所以1a ＋1b≥22， 即1a ＋1b的最小值为2 2. 11．已知x >0，y >0，且2x ＋5y ＝20.(1)求u ＝lg x ＋lg y 的最大值； (2)求1x ＋1y的最小值． 解 (1)∵x >0，y >0，∴由基本不等式，得2x ＋5y ≥210xy .∵2x ＋5y ＝20，∴210xy ≤20，xy ≤10，当且仅当2x ＝5y 时，等号成立．因此有⎩⎪⎨⎪⎧ 2x ＋5y ＝20，2x ＝5y ，解得⎩⎪⎨⎪⎧x ＝5，y ＝2， 此时xy 有最大值10.∴u ＝lg x ＋lg y ＝lg(xy )≤lg 10＝1.∴当x ＝5，y ＝2时，u ＝lg x ＋lg y 有最大值1.(2)∵x >0，y >0，∴1x ＋1y ＝⎝⎛⎭⎫1x ＋1y ·2x ＋5y 20＝120⎝⎛⎭⎫7＋5y x ＋2x y ≥120⎝⎛⎭⎫7＋25y x ·2x y ＝7＋21020，当且仅当5y x ＝2x y时，等号成立． 由⎩⎪⎨⎪⎧ 2x ＋5y ＝20，5y x ＝2x y ，解得⎩⎪⎨⎪⎧ x ＝1010－203，y ＝20－4103.∴1x ＋1y 的最小值为7＋21020. 12.某人准备在一块占地面积为1 800平方米的矩形地块中间建三个矩形温室大棚，大棚周围均是宽为1米的小路(如图所示)，大棚占地面积为S 平方米，其中a ∶b ＝1∶2.(1)试用x ，y 表示S ；(2)若要使S 的值最大，则x ，y 的值各为多少？解 (1)由题意可得xy ＝1 800，b ＝2a ，则y ＝a ＋b ＋3＝3a ＋3，所以S ＝(x －2)a ＋(x －3)b ＝(3x －8)a＝(3x －8)y －33＝1 808－3x －83y (x >3，y >3)． (2)方法一 S ＝1 808－3x －83×1 800x＝1 808－⎝⎛⎭⎫3x ＋4 800x ≤1 808－23x ×4 800x＝1 808－240＝1 568，当且仅当3x ＝4 800x， 即x ＝40时等号成立，S 取得最大值，此时y ＝1 800x＝45， 所以当x ＝40，y ＝45时，S 取得最大值．方法二 设S ＝f (x )＝1 808－⎝⎛⎭⎫3x ＋4 800x (x >3)， 则f ′(x )＝4 800x 2－3＝3(40－x )(40＋x )x 2， 令f ′(x )＝0，则x ＝40，当0<x <40时，f ′(x )>0；当x >40时，f ′(x )<0.所以当x ＝40时，S 取得最大值，此时y ＝45.13．(2018·郑州模拟)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，若2a －c b ＝cos C cos B，b ＝4，则△ABC 面积的最大值为( )A ．4 3B ．2 3C ．3 3 D. 3答案 A解析 ∵2a －c b ＝cos C cos B， ∴(2a －c )cos B ＝b cos C ，由正弦定理得(2sin A －sin C )cos B ＝sin B cos C ，∴2sin A cos B ＝sin C cos B ＋sin B cos C＝sin(B ＋C )＝sin A .又sin A ≠0，∴cos B ＝12. ∵0<B <π，∴B ＝π3. 由余弦定理得b 2＝16＝a 2＋c 2－2ac cos π3＝a 2＋c 2－ac ≥2ac －ac ＝ac ，∴ac ≤16，当且仅当a ＝c 时等号成立．∴S △ABC ＝12ac sin π3≤12×16×32＝4 3. 故△ABC 面积的最大值为4 3.故选A.14．如图，在△ABC 中，点D ，E 是线段BC 上两个动点，且AD →＋AE → ＝xAB →＋yAC →，则1x ＋4y 的最小值为( )A ．32B ．2C ．52D ．92答案 D解析 设AD →＝mAB →＋nAC →，AE →＝λAB →＋μAC →，∵B ，D ，E ，C 共线，∴m ＋n ＝1，λ＋μ＝1，∵AD →＋AE →＝xAB →＋yAC →＝()m ＋λAB →＋()n ＋μAC →，则x ＋y ＝m ＋n ＋λ＋μ＝2，∴1x ＋4y ＝12⎝⎛⎭⎫1x ＋4y ()x ＋y ＝12⎝⎛⎭⎫5＋y x ＋4x y ≥12⎝⎛⎭⎫5＋2y x ·4x y ＝92，当且仅当x ＝23，y ＝43时，等号成立． 故1x ＋4y 的最小值为92，故选D.15．设S n 为数列{a n }的前n 项和，已知a 1＝2，对任意p ，q ∈N *，都有a p ＋q ＝a p ·a q ，则f (n )＝S n －1·(S n －1＋2)＋256a n的最小值为_______． 答案 30解析 当q ＝1时，a p ＋1＝a p ·a 1＝2a p ，∴数列{a n }是首项为2，公比为2的等比数列，∴a n ＝2n ，S n ＝2(2n －1)2－1＝2n ＋1－2， ∴S n －1＝2n －2，S n －1·(S n －1＋2)＝(2n －2)·2n ，∴f (n )＝(2n －2)2n ＋2562n ＝2n －2＋2562n ≥2256－2＝30，当且仅当2n ＝16，即n ＝4时，等号成立，f (n )min ＝30.16．已知正三棱柱ABC －A 1B 1C 1，侧面BCC 1B 1的面积为46， 求该正三棱柱外接球表面积的最小值．解 设BC ＝a ，CC 1＝b ，则ab ＝46，底面三角形外接圆的半径为r ，则a sin 60°＝2r ，∴r ＝33a . 所以R 2＝⎝⎛⎭⎫b 22＋⎝⎛⎭⎫33a 2＝b 24＋a 23≥2 b 24·a 23＝29612＝42， 当且仅当a ＝32b 时，等号成立． 所以该正三棱柱外接球表面积的最小值为4π×42＝162π.。

高一数学讲义 第七章 平面向量7.1 向量的基本概念及表示现实生活中，有些量在有了测定单位之后只需用一个实数就可以表示，例如温度，时间，面积，这些只需用一个实数就可以表示的量叫作标量．还有些量不能只用一个实数表示，例如位移，力，速度等既有大小又有方向的量，这些既有大小又有方向的量叫作向量．向量既有大小又有方向，因此向量不能比较大小．数学中常用平面内带有箭头的线段来表示平面向量．以线段的长来表示向量的大小：以箭头所指的方向（即从始点到终点的方向）来表示向量的方向．一般地，以点P 为始点，点Q 为终点的向量记作PQ ．为书写简便，在不强调向量的起点与终点时，向量也可以用一个小写的字母并在上面画一个小箭头来表示，如a ．PQ 的大小叫作PQ 的模，记作PQ ，类似地，a 的模记作a ． 1．零向量：长度为0的向量叫做零向量，记作0；0的方向是任意的． 2．单位向量：长度为1的向量叫做单位向量．3．平行向量：方向相同或相反的向量叫做平行向量（也叫共线向量）． 4．相等向量：长度相等且方向相同的向量叫做相等向量．5．负向量：与a 的模相等，方向相反的向量叫作a 的负向量，记作a -．我们规定：0的相反向量仍是零向量．易知对任意向量a 有()a a --=．向量共线与表示它们的有向线段共线不同：向量共线时表示向量的有向线段可以是平行的，不一定在一条直线上；而有向线段共线则线段必须在同一条直线上．规定。

与任一向量平行．图7-1图7-1三个向量a 、b 、c 所在的直线平行，易知这三个向量平行，记作a b c ∥∥，我们也可以称这三个向量共线．例l ．如图7-2所示，128A A A 、是O 上的八个等分点，则在以128A A A 、及圆O 九个点中任意两点为起点与终点的向量中，模等于半径的向量有多少??A 8A 7A 6A 5A 4A 3A 2A 1图7-2解：（1）模等于半径的向量只有两类，一类是()128i OA i =、共8个；另一类是()128iAO i =、也有8个．两类合计16个． （2）以128A A A 、为顶点的O 的内接正方形有两个，一个是正方形1257A A A A ；另一个是正方形2468A A A A ．在题中所述的向量中，只有这两个正方形的边（看成有向线段，每一边对应两个向量）的√2倍的向量共有42216⨯⨯＝个． 注意：（1）在模等于半径的向量个数的计算中，要计算i OA 与()128i AO i =、两类．一般地我们易想到()128i OA i =、这8个，而易遗漏()128iAO i =、这8个．（2的两个向量，例如边13A A 对应向量13A A 与31A A ，因此与（1）一样，在解题过程中主要要防止漏算．认为满足条件的向量个数为8是错误的．例2．在平面中下列各种情形中，将各向量的终点的集会分别构成什么图形? （1）把所有单位向量的起点平移到同一点O ．（2）把平行于直线l 的所有单位向量的起点平移到直线l 上的p 点． （3）把平行于直线l 的所有向量的起点平移到直线l 的点p ． 解：（1）以点O 为圆心，l 为半径的圆．（2）直线l 上与点p 的距离为1个长度单位的两个点． （3）直线l ．例3．判断下列命题的真假：①直角坐标系中坐标轴的非负轴都是向量； ②两个向量平行是两个向量相等的必要条件；③向量AP 与CD 是共线向量，则A 、B 、C 、D 必在同一直线上； ④向量a 与向量b 平行，则a 与b 的方向相同或相反； ⑤四边形ABCD 是平行四边形的宽要条件是AB DC =．解：①直角坐标系中坐标轴的非负半轴，虽有方向之别，但无大小之分，故命题是错误的．②由于两个向量相等，必知这两个向量的方向与长度均一致，故这两个向量一定平行，所以，此命题正确； ③不正确．AB 与CD 共线，可以有AB 与CD 平行；④不正确．如果其中有一个是零向量，则其方向就不确定；⑤正确．此命题相当于平面几何中的命题：四边形ABCD是平行四边形的充要条件是有一组对边平行且相等．1．下列各量中是向量的有__________．（A）动能（B）重量（C）质量（D）长度（F）作用力与反作用力（F）温度2．判断下列命题是否正确，若不正确，请简述理由．①向量AB与CD是共线向量，则A、B、C、D四点必在一直线上；②单位向量都相等；③任一向量与它的相反向量不相等；④共线的向量，若起点不同，则终点一定不同．3．回答下列问题，并说明理由．（1）平行向量的方向一定相同吗?（2）共线向量一定相等吗?（3）相等向量一定共线吗?不相等的向量一定不共线吗?4．命题“a b∥，b c∥（）∥，则a bA．总成立B．当0a ≠时成立C．当0b ≠时成立D．当0c ≠时成立5．已知正六边形ABCDEF（见图7-3），在下列表达式中：①BC CD EC+；③FE ED++；②2BC DC+；④2ED FA-；与AC相等的有__________．CF图737.2向量的加减法两个向量可以求和．一般地，对于两个互不平行的向量a、b，以A为共同起点平移向量，有AB a=，=叫作a和b这两个向量的和，即AD b=，则以AB、AD为邻边的平行四边形ABCD的对角线AC c+=．求两个向量和的运算叫做向量的加法．上述求两个向量的和的方法称为向量加法的平行四a b c边形法则，见图7-4．平行四边形法则B图74又AD BC = AB BC AC ∴+=由此发现，当第二个向量的始点与第一个向量的终点重合时．这两个向量的和向量即为第一个向量的始点指向第二个向量终点的向量．此法则称为向量加法的三角形法则，地图7-5．三角形法则图75特殊地．求两个平行向量的和，也可以用三角形法则进行（如图7-6）：（b ）（a ）a BA图76显然，对于任何a ，有0a a +=；()0a a +-=． 对于零向量与任一向量a ，有00a a a +=+=．向量的加法具有与实数加法类似的运算性质，向量加法满足交换律与结合律： 交换律：a b b a +=+结合律：()()a b c a b c ++=++与实数的减法相类似，我们把向量的减法定义为向量加法的逆运算．若向量a 与b 的和为向量c ，则向量b 叫做向量c 与a 的差，记作b c a =-．求向量差的运算叫做向量的减法．由向量加法的三角形法则以及向量减法的定义．我们可得向量减法的三角形法则，其作法：在平面内取一点O，作OA a=-，即a b-声可以表示为从向量b的终点指向向=，则BA a b=，OB b量a的终点的向量．注意差向量的“箭头”指向被减向量，见图7-7．CB图77此外，我们可以先做向量b的负向量OB b′，可根据向量加法的平行四边形法则得()=-OC a b=+-．易知向量OC BA=，因此，()+-=-．a b a b例1．如图7-8所示，已知向量a，b，c，试求作和向量a b c++．图78分析：求作三个向量的和的问题，首先求作其中任意两个向量的和，因为这两个向量的和仍为一个向量，然后再求这个新向量与另一个向量的和．即可先作a b+，再作()++．a b c解：如图7-9所示，首先在平面内任取一点O，作向量OA a=+，=，再作向量AB b=，则得向量OB a b然后作向量BC c=++即为所求．=，则向量OC a b cO图79例2．化简下列各式（1）AB CA BC ++； （2）OE OF OD DO -+--．解：（1）原式()0AB BC CA AB BC CA AC CA AC AC =++=++=+=-= （2）原式()()0OE OF OD DO EO OF EF =+-+=+-=例3．用向量方法证明：对角线互相平分的四边形是平行四边形．分析：要证明四边形是平行四边形只要证明某一组对边平行且相等．由相等向量的意义可知，只需证明其一组对边对应的向量是相等向量．已知：如图7-10，ABCD 是四边形，对角线AC 与BD 交于0，且AO OC =，DO OB =．ODCBA图710求证：四边形ABCD 足平行四边形． 证明：由已知得AO OC =，BO OD =，AD AO OD OC BO BO OC BC =+=+=+=，且A D B C ，，，不在同一直线上，故四边形ABCD 是平行四边形．例4．已知平面上有不共线的四点O A B C ，，，．若320OA OB OC -+=，试求AB BC的值．解：因为23OA OC OB +=，所以()2OB OA OC OB -=-．于是有2AB BC =-．因此2AB BC=．基础练习1．若对n 个向量12n a a a ，，，存在n 个不全为零的实数12n k k k ，，，，使得11220n n k a k a k a +++=成立，则称向量12n a a a ，，，为“线性相关”，依此规定，能说明()110a =，，()211a =-，，()322a =，“线性相关”的实数123k k k ，，依次可以取____________________（写出一组数值即可，不必考虑所有情况）．2．已知矩形ABCD 中，宽为2，长为AB a =，BC b =，AC c =，试作出向量a b c ++，并求出其模的大小．3．设a ，b 为两个相互垂直的单位向量．已知OP a =，OR ra kb =+．若PQR △为等边三角形，则k ，r 的取值为（ ）A．k r == B．k r =C．k r ==D．k r = 4．若A B C D 、、、是平面内任意四点，则下列四式中正确的是（ ）①AC BD BC AD +=+ ②AC BD DC AB -=+ ③AB AC DB DC --=④AB BC AD DC +-=A ．1B ．2C ．3D ．45．设a 表示“向东走10km ”，b 表示“5km ”，c 表示“向北走10km ”，d 表示“向南走5km ”．说明下列向量的意义．（1）a b +；（2）b d +；（3）d a d ++．6．在图7-11的正六边形ABCDEF 中，AB a =，AF b =，求AC ，AD ，AE ．FC图7117.3 实数与向量的乘法如图7-12，已知非零向量a ，可以作出a a a ++和()()()a a a -+-+-．P Q M N aaa-a图712aOC OA AB BC a a a =++=++，简记3OC a =；同理有()()()3PN PQ QM MN a a a a =++=-+-+-=-．观察得：3a 与a 方向相反相反且33a a -=．一般地，实数λ与向量a 的积是一个向量，记作：a λ．a λ的模与方向规定如下：（1）a a λλ=；（2）a λ的方向定义为：0λ>时a λ与a i 方向相同；0λ<时a λ与a i 方向相反；0λ=或0a =时规定：0a λ=．以上规定的实数与向量求积的运算叫作实数与向量的乘法（简称向量的数乘）．向量数乘的几何意义就是：把向量a 沿向量a 的方向或反方向放大或缩小，a λ与a 是互相平行的向量．对于任意的非零向量a ，与它同方向的单位向量叫做向量a 的单位向量，记作0a ．易知01a a a =．向量共线定理：如果有一个实数λ，使()0b a a λ=≠，那么b 与a 是共线向量；反之，如果b 与()0a b ≠是共线向量，那么有且只有一个实数λ，使得b a λ=．通过作图，可以验证向量数乘满足以下运算定律：当m 、n ∈R 时，有 1．第一分配律()m n a ma na +=+． 2．第二分配律()m a b ma mb +=+． 3．结合律()()m na mn a =． 例1．计算：（1）()()63292a b a b -+-+；（2）原式12711332236227a a b b a a b ⎛⎫⎛⎫=-+--++ ⎪ ⎪⎝⎭⎝⎭；（3）()()()64222a b c a b c a c -+--+--+． 解：（1）原式18121893a b a b b =---+=-． （2）原式12711332236227a a b b a a b ⎛⎫⎛⎫=-+--++ ⎪ ⎪⎝⎭⎝⎭17732367a b a b ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭ 77106262b a a b =+--=． （3）原式66648442a bc a b c a c =-+-+-+-()()()64468642a a a b b c c c =-++-++-- 62a b =+．例2．已知O 为原点，A ，B ，C 为平面内三点，求证A ，B ，C 三点在一条直线上的充要条件是OC OA OB αβ=+，且αβ∈R ，，1αβ+=．分析：证明三点共线可从三点构成的其中两个向量存在数乘关系．证明必要条件也是从向量共线时向量的数乘关系入手．证明：必要性．设A B C ，，三点共线，则AC 与AB 共线．于是存在实数λ，使AC AB λ=． 而AC OC OA =-，AB OB OA =-，()OC OA OB OA λ∴-=-．()1OC OB OA λλ∴=+-． 令λβ=，1λα-=，有()11αβλλ+=-+=， OC OA OB αβ∴=+，且1αβ+=．充分性．若OC OA OB αβ=+，且1αβ+=，则()1OC OA OB ββ=-+，()OC OA OB OA β=+-，()OC OA OB OC β-=-，AC AB β∴=，β∈R ． AC ∴与AB 共线，而A 为AC 与AB 的公共端点，A B C ∴，，三点在一条直线上．在证明必要性时，A B C ，，三点共线还可用AB kBC =，AC kBC =表示．本题的结论还可有更一般的形式：A B C 、、三点在一条直线上的充要条件是存在实数h ，k ，l ，使0hOA kOB lOC ++=，且1h k l ++=，l k h ，，中至少有一个不为0．例3．如图7-13，设O 为ABC △内一点，PQ BC ∥，且PQt BC=，，OB b =，OC c =，试求OP ，OQ ． 解：由平面几何知，APQ ABC ⨯△∽△，且对应边之比为t ，图713故AP AQ PQt AB AC BC===， 又A P B 、、与A Q C 、、分别共线，即知 AP t AB =，AQ t AC =．()()OP OA AP OA t AB OA t OB OA a t b a ∴=+=+=+-=+-，即()1OP t a tb =-+，()()OQ OA AQ OA t AC OA t OC OA a t c a =+=+=+-=+-， 即()1OQ t a c =-+．例4．设两非零向量1e 和2e 不共线，（1）如果12AB e e =+，1228BC e e =+，()123CD e e =-，求证A B D ，，三点共线． （2）试确定实数k ，使12ke ke +共线． （1）证明12AB e e =+，()121212283355BD BC CD e e e e e e AB =+=++-=+=，AB BD ∴，共线，又有公共点B A B D ∴，，三点共线．（2）解12ke e +与12e ke +共线，∴存在λ使()1212ke e e ke λ+=+， 则()()121k e k e λλ-=-，由于1e 与2e 不共线， 只能有010k k λλ-=⎧⎨-=⎩则1k =±．例5．在ABC △中，F 是BC 中点，直线l 分别交AB AF AC ，，于点D ，G ，E （见图7-14）．如果AD AB λ=，AE AC μ=，λ，μ∈R ．证明：G 为ABC △重心的充分必要条件是113λμ+=．l GF E DCB A图714解：若G 为ABC △重心，则()221332AG AF AB AC ==⋅+=13AD AE λμ⎛⎫+ ⎪ ⎪⎝⎭． 又因点D G E ，，共线，所以，()113AD AE AG t AD t AE λμ⎛⎫=+-=+ ⎪ ⎪⎝⎭， 因AD ，AE 不共线，所以，13t λ=且113t μ=-，两式相加即得113λμ+=． 反之，若113λμ+=，则()2xAG xAF AB AC ==+()12x AD AE t AD t AE λμ⎛⎫=+=+- ⎪ ⎪⎝⎭， 所以，2x t λ=且12x t μ=-，相加即得23x =，即G 为ABC △重心． 基础练习1．已知向量a 、b 是两非零向量，在下列四个条件中，能使a 、b 共线的条件是（ ） ①234a b e -=且23a b e +=-；②存在相异实数λ、u ，使0a ub λ+=； ③0xa yb +=（其中实数x y 、满足0x y +=）； ④已知梯形ABCD 中，其中AB a =、CD b =． A ．①② B ．①③C ．②④D ．③④2．判断下列命题的真假：（1）若AB 与CD 是共线向量，则A B C D ，，，四点共线． （2）若AB BC CA ++=0，则A B C ，，三点共线． （3）λ∈R ，则a a λ>．（4）平面内任意三个向量中的每一个向量都可以用另外两个向量的线性组合表示． 3．已知在ABC △中，D 是BC 上的一点，且BDDCλ=，试求证：1AB AC AD λλ+=+． 4．已知3AD AB =，3DE BC =．试判断AC 与AE 是否共线．5．已知在四边形ABCD 中，2AB a b =+，4BC a b =--，53CD a b =--，求证：四边形ABCD 是梯形．6．已知()2cos A αα，()2cos B ββ，()10C -，是平面上三个不同的点，且满足关系式CA BC λ=，求实数λ的取值范围．7．已知梯形ABCD 中，2AB DC =，M N ，分别是DC AB 、的中点，若1AB e =，2AD e =，用1e ，2e 表示DC BC MN 、、．8．四边形ABCD 是一个梯形，AB CD ∥且2AB CD =，M N 、分别是DC 和AB 的中点，已知AB a =，AD b =，试用a ，b 表示BC 和MN ．9．已知a b 、是不共线的非零向量，11c a b λμ=+，22d a b λμ=+，其中1122λμλμ、、、为常数，若c d ma nb +=+，求m n 、的值．10．设a 、b 是不共线的两个非零向量，OM ma =，ON nb =，OP a b αβ=+，其中m n αβ、、、均为实数，0m ≠，0n ≠，若M P N 、、三点共线，求证：1mnαβ+=．11．在ABC △中，BE 是CD 交点为P ．设AB a =，AC b =，AP c =，AD a λ=，（01λ<<），()01AE b μμ=<<，试用向量a ，b 表示c ．12．在平面直角坐标系中，O 为坐标原点，设向量()12OA =，，()21OB =-，若OP xOA yOB =+且12x y ≤≤≤，则求出点P 所有可能的位置所构成的区域面积．7.4 向量的数量积数量积定义：一般地．如果两个非零向量a 与b 的夹角为α．我们把数量cos a b α⋅叫做a 与b 的数量积（或内积），记作：a b ⋅，即：cos a b a b α⋅=⋅，其中记法“a b ⋅”中间的“⋅”不可以省略，也不可以用“×”代替．特别地，a b ⋅可记作2a ．规定：0与任何向量的数量积为0．非零向量夹角的范围：0≤口≤Ⅱ．投影的定义：如果两个非零向量a 与b 的夹角为α，则数量cos b θ称为向量b 在a 方向上的投影．注意：投影是一个数量．数量积的几何意义：如图7-15，我们把cos b α<叫做向量b 在a 方向上的投影，即有向线段1OB 的数量．图715当π02α<≤时，1OB 的数量等于向量1OB 的模1OB ； 当ππ2α<≤时，1OB 的数量等于向量1OB 的模－1OB ； 当π2α=时，1OB 的数量等于零． 当然，cos a α即为a 在b 方向上的投影．综上，数量积的几何意义：a b ⋅等于其中一个向量a 的模a 与另一个向量b 在a 的方向上的投影cos b α的乘积．向量的数量积的运算律： ①a b b a ⋅=⋅②()()()a b b a b λλλ⋅⋅=⋅（λ为实数）③()a b c a c b c +⋅=⋅+⋅ 鉴于篇幅这里仅证明性质②：证明：（1）若0λ>，()cos a b a b λλθ⋅=，()cos a b a b λλθ⋅=，()cos a b a b λλθ⋅=，（2）若0λ<，()()()cos πcos cos a b a b a b a b λλθλθλθ⋅=-=--=，()cos a b a b a b λλλθ⋅=⋅=，()()()cos πcos a b a b a b λλθλθ⋅=-=--=cos a b λθ． （3）若0λ=，则()()()0a b a b a b λλλ⋅=⋅=⋅=． 综合（1）、（2）、（3），即有()()()a b a b a b λλλ⋅=⋅=⋅．例1．已知4a =，5b =，当（1）a b ∥，（2）a b ⊥，（3）a 与b 的夹角为30︒时，分别求a 与b 的数量积．解：（1）a b ∥，若a 与b 同向，则0θ=︒，cos04520a b a b ∴⋅=⋅︒=⨯=； 若a 与b 反向，则180θ=︒，()cos18045120a b a b ∴⋅=⋅︒⨯⨯⨯-=-． （2）当a b ⊥时，90θ=︒，cos900a b a b ∴⋅=⋅︒=．（3）当a 与b 的夹角为30︒时，cos3045a b a b ⋅=⋅︒=⨯= 例2．空间四点A B C D 、、、满足3AB =，7BC =，11CD =，9DA =，则AC BD ⋅的取值有多少个？解：注意到2222311113079+==+，由于0AB BC CD DA +++=， 则()()2222222DA DA AB BC CDAB BC CD AB BC BC CD CD AB ==++=+++⋅+⋅+⋅()()2222AB BC CD AB BC BC CD =-+++⋅+，即222220AC BD AD BC AB CD ⋅=+--=，AC BD ∴⋅只有一个值0．例3．已知a b 、都是非零向量，且3a b +与75a b -垂直，4a b -与72a b -垂直，求a b 、的夹角． 解：由()()223750716150a b a b a a b b +⋅-=⇒+⋅-= ①()()22472073080a b a b a a b b -⋅-=⇒-⋅+=②两式相减：22a b b ⋅=代入①或②得：22a b =． 不妨设a b 、的夹角为θ，则221cos 22a b ba bbθ⋅===，又因为0πθ≤≤，60θ∴=︒．例4．在凸四边形ABCD 中，P 和Q 分别为对角线BD 和AC 的中点，求证：2222224AB BC CD DA AC BD PQ +++=++．证明：联结BQ ，QD ，因为BP PQ BQ +=，DP PQ DQ +=， 所以()()2222BQ DQ BP PQ DP PQ +=+++ 222222BP DP PQ BP PQ DP PQ =+++⋅+⋅()22222BP DP PQ BP DP PQ =++++⋅ 2222BP DP PQ =++①又因为BQ QC BC +=，BQ QA BA +=，0QA QC +=， 同理222222BA BC QA QC BQ +=++② 222222CD DA QA QC QD +=++③由①、②、③可得()()2222222224222BA BC CD QA BQ QD AC BP PQ ++=++=++= 2224AC BD PQ ++．得证．例5．平面四边形ABCD 中，AB a =，BC b =，CD c =，DA d =，且a b b c c d d a ⋅=⋅=⋅=⋅，判断四边形ABCD 的形状．证明：由四边形ABCD 可知，0a b c d +++=（首尾相接）()a b c d ∴+=-+，即()()22a bc d +=+展开得222222aa b b c c d d +⋅+=+⋅+a b c d ⋅=⋅，222a b c d ∴+=+①同理可得2222a dbc +=+② ①-②得2222b a ac =⇒=，b d ∴=，ac =，即AB CD =，BC DA =， 故四边形ABCD 是平行四边形．由此a c =-，bd =-．又a b b c ⋅=⋅，即()0b a c -=()20b a ∴⋅=即a b AB BC ⊥⇒⊥， 故四边形ABCD 是矩形．例6．已知非零向量a 和b 夹角为60︒，且()()375a b a b +⊥-，求证：()()472a b a b -⊥-．证明：因为a 和b 夹角为60︒，所以1cos602a b a b a b ⋅=⋅⋅︒=⋅；又因为()()375a b a b +⊥-，所以，即()()3750a b a b +⋅-=．22222217161571615781502a ab b a a b b a a b b +⋅-=+⨯⋅-=+⋅-=． ()()7150a b a b ∴+⋅-=，0a b ∴-=，即a b =．因为()()22222214727308730871582a b a b a a b b a a b b a a b b -⋅-=-⋅+=-⨯+=-+，把a b =代入上式消去b 得()()2247271580a b a b a a a a -⋅-=-+=．所以()()472a b a b -⊥-．基础练习1．已知a b c 、、是三个非零向量，则下列命题中真命题的个数为（ ） ①a b a b a b ⋅=⋅⇔∥； ②a b 、反向a b a b ⇔⋅=-⋅； ③a b a b a b ⊥⇔+=-； ④a b a c b c =⇔⋅=⋅． A ．1B ．2C ．3D ．42．已知向量i j ，为相互垂直的单位向量，28a b i j +=-，816a b i j -=-+，求a b ⋅．3．如图7-16所示，已知平行四边形ABCD ，AB a =，AD b =，4a=，2b =，求：OA OB ⋅．C图7164．设6a =，10b =，46a b -=，求a 和b 的夹角θ的余弦值． 5．已知a b ⊥，2a =，3b =，当()()32a b a b λ-⊥+时，求实数λ的值．6．已知不共线向量a ，b ，3a =，2b =，且向量a b +与2a b -垂直．求：a 与b 的夹角θ的余弦值． 7．已知3a =，4b =，且a 与b 不共线，k 为何值时，向量a kb +与a kb -互相垂直？ 8．在ABC △中，已知4AB AC ⋅=，12AB BC ⋅=-，求AB ．9．在ABC △中，AB a =，BC b =，且0a b ⋅>，则ABC △的形状是__________． 10．已知向量()24a =，，()11b =，．若向量()b a b λ⊥+，则实数λ的值是__________．11．如图7-17，在四边形ABCD 中，4AB BD DC ++=，0AB BD BD DC ⋅=⋅=，4AB BD BD DC ⋅+⋅=，求()AB DC AC +⋅的值．图717DCBA能力提高12．如图7-18，在Rt ABC △中，已知BC a =，若长为2a 的线段PQ 以点A 为中点．问PQ 与BC 的夹角θ为何值时，BP CQ ⋅的值最大?并求出这个最大值．PQ图71813．已知ABC △中满足()2ABAB AC BA BC CA CB =⋅+⋅+⋅，a b c 、、分别是ABC △的三边．试判断ABC △的形状并求sin sin A B +的取值范围．14．设边长为1的正ABC △的边BC 上有n 等分点，沿点B 到点C 的方向，依次为121n P P P -，，，，若1121n n S AB AP AP AP AP AC -=⋅+⋅++⋅，求证：21126n n S n-=．15．在ABC △中，AB a =，BC c =，CA b =，又()()()123c b b a a c ⋅⋅⋅=∶∶∶∶，则ABC △三边长之比a b c =∶∶__________．16．在向量a b c ，，之间，该等式()()())132a b c a b b c c a ⎧++=⎪⎨⋅⋅⋅=-⎪⎩∶∶∶成立，当1a =时，求b 和c 的值．17．若a b c ，，中每两个向量的夹角均为60︒，且4a =，6b =，2c =，求a b c ++的值． 7.5 向量的坐标表示及其运算向量的坐标表示在平面直角坐标系中，每一个点都可用一对实数()x y ，来表示，那么，每一个向量可否也用一对实数来表示?前面的平面向量分解告诉我们，只要选定一组基底，就有唯一确定的有序实数对与之一一对应． 我们分别选取与x 轴、y 轴方向相同的单位向量i ，j 作为基底，由平面向量的基本定理．对于任一向量a ，存在唯一确定的实数对()x y ，使得()a xi y j x y =+∈R ，，我们称实数对()x y ，叫向量a 的坐标，记作()a x y =，．其中x 叫向量a 在x 轴上的坐标,y 叫向量a 在y 轴上的坐标，见图7-19．图719注意：（1）与a 相等的向量的坐标也是()x y ，．（2）所有相等的向量坐标相同；坐标相同的向量是相等的向量． 平面向量的坐标运算（1）设()11a x y =，，()22b x y =，，则()1212a b x x y y +=++，． （2）设()11a x y =，，()22b x y =，，则()1212a b x x y y -=--，． （3）设()11A x y ，，()22B x y ，，则()2121AB OB OA x x y y =-=--，． （4）设()11a x y =，，λ∈R ，则()a x y λλλ=，．（5）设()11a x y =，，()22b x y =，，则()1212a b x x y y ⋅=+． 向量平行的坐标表示设()11a x y =，，()22b x y =，，且0b ≠，则()1212a b x x y y =+∥． 向量的平行与垂直的充要条件设()11a x y =，，()22b x y =，，且0b ≠，0a ≠则 12210a b b a x y x y λ⇔=⇔-=∥． 121200a b a b x x y y ⊥⇔⋅=⇔+=．重要的公式（1）长度公式：2221a a a x y ===+()()11a x y =，（2）夹角公式：()())1122cos a x y b x y θ===，，，．（3）平面两点间的距离公式： (()())1122A B d AB AB AB x A x y B xy ==⋅=，，，，．（4）不等式：cos a b a b a b θ⋅=≥．例1．已知()12a a a =，，()12b b b =，，且12210a b a b -≠，求证：（1）对平面内任一向量()12c c c ，，都可以表示为()xa yb x y +∈R ，的形式； （2）若0xa yb +=，则0x y ==．证明：（1）设c xa yb =+，即()()()()1212121122c c x a a y b b a x b y a x b y =+=++，，，，， 111222.a xb yc a x b y c +=⎧∴⎨+=⎩，12210a b a b -≠，∴上述关于x y ，的方程组有唯一解．1221122112211221.c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩，1221122112211221c b c b a c a c c a b a b a b a b a b --∴=+--． （2）由（1）的结论，0c =，即120c c ==，则 122112210c b c b x a b a b -==-，122112210a c a c y a b a b -==-，0x y ∴==． 小结：证明（1）的过程就是求实数x ，y 的过程，而12210a b a b -≠是上面二元一次方程组有唯一解的不可缺少的条件．另外，本题实际上是用向量的坐标形式表述平面向量基本定理．其中1x λ=，2y λ=，这里给出了一个具体的求12λλ，的计算方法．例2．向量()10OA =，，()11OB =，，O 为坐标原点，动点()P x y ，满足0102OP OA OP OB ⎧⋅⎪⎨⋅⎪⎩≤≤≤≤，求点()Q x y y +，构成图形的面积．解：由题意得点()P x y ，满足0102x x y ⎧⎨+⎩≤≤≤≤，令x y uy v +=⎧⎨=⎩，则点()Q u v ，满足0102u v u -⎧⎨⎩≤≤≤≤，在uOv 平面内画出点()Q u v ，构成图形如图7-20所示，∴其面积等于122⨯=．图720例3．在直角坐标系中，已知两点()11A x y ，，()22B x y ，；1x ，2x 是一元二次方程222240x ax a -+-=两个不等实根，且A B 、两点都在直线y x a =-+上． （1）求OA OB ⋅；（2）a 为何值时OA 与OB 夹角为π3． 解：（1）12x x 、是方程222240x ax a -+-=两个不等实根，()224840a a ∴∆=-->解之a -<()212142x x a =-，12x x a +=又A B 、两点都在直线y x a =-+上，()()()()2212121212142y y x a x a x x a x x a a ∴=-+-+=-++=- 121224OA OB x x y y a ∴⋅=+=-（2）由题意设1x =，2x =112y x a x ∴=-+==，同理21y x =(()22212121224OA OB xx x x x x x ∴==+=+-=当OA 与OB夹角为π3时，π1cos 4232OA OBOA OB ⋅==⨯= 242a ∴-=解之(a =- a ∴=即为所求． 例4．已知()10a =，，()21b =，． ①求3a b +；②当k 为何实数时，ka b -与3a b +平行，平行时它们是同向还是反向？解：①()()()31032173a b +=+=，，，，2373a b ∴+=+ ②()()()102121ka b k k -=-=--，，，． 设()3ka b a b λ-=+，即()()2173k λ--=，，， 12731313k k λλλ⎧=-⎪-=⎧⎪∴⇒⎨⎨-=⎩⎪=-⎪⎩．故13k =-时，它们反向平行．例5．对于向量的集合(){}221A v x y x y ==+，≤中的任意两个向量12v v 、与两个非负实数αβ、；求证：向量12v v αβ+的大小不超过αβ+．证明：设()111v x y =，，()222v x y =，，根据已知条件有：22111x y +≤，22221x y +≤， 又因为(12v v αβα+==其中12121x x y y +所以12v v αβααβαβ+=+=+≤． 基础练习1．已知()21a =，，()34b =-，，求a b +，a b -，34a b +的坐标． 2．设O 点在ABC △内部，且有230OA OB OC ++=，求ABC △的面积与AOC △的面积的比． 3．已知平行四边形ABCD 的三个顶点A B C ，，的坐标分别为（-2，1），（-1，3），（3，4），求顶点D 的坐标．4．已知向量i ，j 为相互垂直的单位向量，设()12a m i j =+-，()1b i m j =+-，()()a b a b +⊥-，求m 的值．5．已知等腰梯形ABCD ，其中AB CD ∥，且2DC AB =，三个顶点()12A ，，()21B ，，()42C ，，求D 点的坐标．6．如图7-21所示，已知()20OA =，，(1OB =，将BA 绕着B 点逆时针方向旋转60︒，且模伸长到BA 模的2倍，得到向量BC ．求四边形AOBC 的面积S ．图7217．如图7-22所示，已知四边形ABCD 是梯形，AD BC ∥，2BC AD =，其中()12A ，，()31B ，，()24D ，，求C 点坐标及AC 的坐标．图7228．已知向量()2334a x x x =+--，与AB 相等，其中()12A ，，()32B ，，求x ． 9．平面内有三个已知点()12A -，，()70B ，，()56C -，，求 （1）AB ，AC ；（2）AB AC +，AB AC -；（3）122AB AC +，3AB AC -． 10．已知向量()12a =，，()1b x =，，2u a b =+，2v a b =-，且u v ∥，求x ． 11．已知()23a =，，()14b =-，，()56c =，，求()a b c ⋅，和()a b c ⋅⋅．12．已知两个非零向量a 和b 满足()28a b +=-，，()64a b -=--，，求a 与b 的夹角的余弦值． 能力提高13．已知平面上三个向量a ，b ，c 均为单位向量，且两两的夹角均为120︒，若()1ka b c k ++>∈R ，求k 的取值范围．14．已知OA ，OB 不共线，点C 分AB 所成的比为2，OC OA OB λμ=+，求λμ-． 7.6 线段的定比分点公式与向量的应用线段的定比分点公式设点P 是直线12P P 上异于1P 、2P 的任意一点，若存在一个实数()1λλ≠-，使12PP PP λ=，则λ叫做点P 分有向线段12P P 所成的比，P 点叫做有向线段12P P 的以定比为λ的定比分点．当P 点在线段12P P 上时0λ⇔≥；当P 点在线段12P P 的延长线上时1λ⇔<-； 当P 点在线段21P P 的延长线上时10λ⇔-<<；设()111P x y ，，()222P x y ，，()P x y ，是线段12P P 的分点，λ是实数且12P P PP λ=，则121211x x x OP y y y λλλλ+⎧=⎪⎪+⇔=⎨+⎪=⎪+⎩()12121111OP OP OP tOP t OP t λλλ+⎛⎫⇔=+-= ⎪++⎝⎭．()1λ≠-由线段的定比分点公式得：中点坐标公式设()111P x y ，，()222P x y ，，()P x y ，为12P P 的中点，（当1λ=时） 得121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩三角形的重心坐标公式ABC △三个顶点的坐标分别为()11A x y ，、()22B x y ，、()33C x y ，，则ABC △的重心的坐标是12312233x x x y y y G ++++⎛⎫ ⎪⎝⎭，． 利用向量可以解决许多与长度、距离及夹角有关的问题．向量兼具几何特性和代数特性，成为沟通代数、三角与几何的重要工具，同时在数学、物理以及实际生活中都有着广泛的应用． 三角形五“心”向量形式的充要条件设O 为ABC △所在平面上一点，角A ，B ，C 所对边长分别为a ，b ，c 则（1）O 为ABC △的外心222OA OB OC ⇔==． （2）O 为ABC △的重心0OA OB OC ⇔++=．（3）O 为ABC △的垂心OA OB OB OC OC OA ⇔⋅=⋅=⋅． （4）O 为ABC △的内心0aOA bOB cOC ⇔++=． （5）O 为ABC △的A ∠的旁心()aOA b OB cOC ⇔=+．例1．如图7-23所示，已知矩形ABCD 中，()21A ，，()54B ，，()36C ，，E 点是CD 边的中点，联结BE 与矩形的对角线AC 交于F 点，求F 点坐标．图723解：四边形ABCD 是矩形，E 是CD 边的中点，ABF CEF ∴△∽△，且2AB CE =2AF CF ∴=即点F 分AC 所成的比2λ=．设()F x y ，．由(21)A ，，(36)C ，，根据定比分点坐标公式得2238123x +⨯==+，12613123y +⨯==+ F ∴点坐标是81333⎛⎫⎪⎝⎭，． 例2．证明：()cos cos cos sin sin αβαβαβ-=+．证明：在单位圆O 上任取两点A ，B ，以Ox 为始边，以OA ，OB 为终边的角分别为β，α，见图7-24．β，sin β）B （cos α图724则A 点坐标为()cos sin ββ，，B 点坐标为()cos sin αα，；则向量()cos sin OA ββ=，，()cos sin OB αα=，，它们的夹角为αβ-，1OA OB ==，cos cos sin sin OA OB αβαβ⋅=+， 由向量夹角公式得：()cos cos cos sin sin OA OB OA OBαβαβαβ⋅-==+，从而得证．注意：用同样的方法可证明()cos cos cos sin sin αβαβαβ+=-．例3．证明柯西不等式()()()2222211221212x y x y x x y y +⋅++≥．证明：令()11a x y =，，()22b x y =，（1）当0a =或0b =时，12120a b x x y y ⋅=+=，结论显然成立； （2）当当0a ≠且0b ≠时，令θ为a ，b 的夹角，则[]0πθ∈，1212cos a b x x y y a b θ⋅=+=．又cos 1θ≤，a b a b ∴⋅≤（当且仅当ab ∥时等号成立）． 1212x x y y ∴+()()()2222211221212x y x y x x y y ∴+⋅++≥（当且仅当1212x x y y =时等号成立）． 例4．给定ABC △，求证：G 是ABC △重心的充要条件是0GA GB GC ++=．证明：必要性 设各边中点分别为D E ，，F ，延长AD 至P ，使DP GD =，则2AG GD =GP =． 又因为BC 与GP 互相平分，所以BPCG 为平行四边形，所以BG PC ∥，所以GB CP =． 所以0GA GB GC GC CP PG ++=++=．充分性 若0GA GB GC ++=，延长AG 交BC 于D ，使GP AG =，联结CP ，则GA PG =． 因为0GC PG PC ++=，则GB PC =，所以GB CP ∥，所以AG 平分BC ．同理BG 平分CA ．所以G 为重心． 例5 ABC △外心为O ，垂心为H ，重心为G ．求证：O G H ，，为共线，且12OG GH =∶∶． 证明：首先()()2112333OG OA AG OA AM OA AB AC OA AO OB OC =+=+=++=+++= ()13OA OB OC ++． 其次设BO 交外接圆于另一点E ，则联结CE 后得CE BC ⊥． 又AH BC ⊥，所以AH CE ∥．又EA AB ⊥，CH AB ⊥，所以AHCE 为平行四边形．所以AH EC =． 所以OH OA AH OA EC OA EO OC OA OB OC =+=+=++=++， 即3OH OG =，所以OG 与OH 共线，所以O G H ，，共线． 即12OG GH =∶∶． 注意：O G H ，，所在的直线称为欧拉线．例6．已知ABC △，AD 为中线，求证()2222122BC AD AB AC ⎛⎫=+- ⎪⎝⎭（中线长公式）． 证明：以B 为坐标原点，以BC 所在的直线为x 轴建立如图7-25所示的直角坐标系，图725设()A a b ，，()0C c ，，02c D ⎛⎫⎪⎝⎭，，则()22222024c c AD a b ac a b ⎛⎫=-+-=-++ ⎪⎝⎭，()()22222222221122244BC c c AB AC a b c a b a b ac ⎛⎫⎡⎤⎪+-=++-+-=+-+⎢⎥ ⎪⎣⎦⎝⎭， 从而()2222122BC AD AB AC ⎛⎫ ⎪=+- ⎪⎝⎭，()2222122BC AD AB AC ⎛⎫=+- ⎪⎝⎭． 例7．是否存在4个两两不共线的平面向量，其中任两个向量之和均与其余两个向量之和垂直？解：如图7-26所示，在正ABC △中，O 为其内心，P 为圆周上一点，满足PA ，PB ，PC ，PO 两两不共线，有POCBA图726()()PA PB PC PO +⋅+=()()PO OA PO OB PO OC PO +++⋅++()()22PO OA OB PO OC =++⋅+ ()()22PO OC PO OC =-⋅+ 2240PO OC =-=有()PA PB +与()PC PO +垂直． 同理可证其他情况．从而PA ，PB ，PC ，PO 满足题意、故存在这样四个平面向量．例8．已知向量1OP ，2OP ，3OP 满足条件1230OP OP OP ++=，1231OP OP OP ===，求证：123PP P △是正三角形．解：令O 为坐标原点，可设()111cos sin P θθ，，()222cos sin P θθ，，()333cos sin P θθ， 由123OP OP OP +=-，即()()()112233cos sin cos sin cos sin θθθθθθ+=--，，， 123123cos cos cos sin sin sin θθθθθθ+=-⎧⎪⎨+=-⎪⎩①② 两式平方和()1212cos 11θθ+-+=，()121cos 2θθ-=-，由此可知12θθ-的最小正角为120︒，即1OP 与2OP 的夹角为120︒， 同理可得1OP 与3OP 的夹角为120︒，2OP 与3OP 的夹角为120︒， 这说明123P P P ，，三点均匀分布在一个单位圆上， 所以123PP P △为等腰三角形． 基础练习1．在ABC △中，若321AB BC BC CA AB CA⋅⋅⋅==，则tan A =__________． 2．已知P 为ABC △内一点，且满足3450PA PB PC ++=，那么PAB PBC PCA S S S =△△△∶∶__________． 3．如图7-27，设P 为ABC △内一点，且2155AP AB AC =+，求ABP △的面积与ABC △的面积之比． PCA图7274．已知ABC △的三顶点坐标分别为()11A ，,()53B ，，()45C ，，直线l AB ∥，交AC 于D ，且直线l 平分ABC △的面积，求D 点坐标． 5．已知()23A ，，()15B -，，且13AC AB =，3AD AB =，求点C D 、的坐标． 6．点O 是平面上一定点，A B C ，，是此平面上不共线的三个点，动点P 满足AC AB OP OA AB AC λ⎛⎫ ⎪=++ ⎪⎝⎭，[)0λ∈+∞，．则点P 的轨迹一定通过ABC △的__________心．能力提高7．设x y ∈R ，，i j 、为直角坐标系内x y 、轴正方向上的单位向量，若()2a xi y j =++，()62b xi y j =+-且2216a b +=．（1）求点()M x y ，的轨迹C 的方程；（2）过定点()03，作直线l 与曲线C 交于A B 、两点，设OP OA OB =+，是否存在直线l 使四边形OAPB 为正方形？若存在，求出l 的方程，或不存在说明理由．8．（1）已知4a =，3b =，()()23261a b a b -⋅+=，求a 与b 的夹角θ；（2）设()25OA =，，()31OB =，，()63OC =，，在OC 上是否存在点M ，使MA MB ⊥，若存在，求出点M 的坐标，若不存在，请说明理由． 9．设a b 、是两个不共线的非零向量()t ∈R （1）记OA a =，OB tb =，()13OC a b =+，那么当实数t 为何值时，A B C 、、三点共线？ （2）若1a b ==且a 与b 夹角为120︒，那么实数x 为何值时a xb -的值最小？10．设平面内的向量()17OA =，，()51OB =，，()21OM =，，点P 是直线OM 上的一个动点，求当PA PB ⋅取最小值时，OP 的坐标及APB ∠的余弦值．11．已知向量()11m =，，向量n 与向量m 夹角为3π4，且1m n ⋅=-． （1）求向量n ；（2）若向量n 与向量()10q =，的夹角为π2，向量22sin 4cos 2A p A ⎛⎫= ⎪⎝⎭，，求2n p +的值．12．已知定点()01A ，，()01B -，，()10C ，．动点P 满足：2AP BP k PC ⋅=． （1）求动点P 的轨迹方程；（2）当0k =时，求2AP BP +的最大值和最小值．13．在平行四边形ABCD 中，()11A ，，()60AB =，，点M 是线段AB 的中点，线段CM 与BD 交于点P ．（1）若()35AD =，，求点C 的坐标； （2）当AB AD =时，求点P 的轨迹．14．已知向量()22a =，，向量b 与向量a 的夹角为3π4，且2a b ⋅=-， （1）求向量b ；（2）若()10t =，且b t ⊥，2cos 2cos 2C c A ⎛⎫= ⎪⎝⎭，，其中A C 、是ABC △的内角，若三角形的三内角A B C 、、依次成等差数列，试求b c +的取值范围．。

第七章平面解析几何本章主要包括两个内容：解析几何初步、圆锥曲线．1．解析几何初步的内容主要是直线与方程、圆与方程和空间直角坐标系，该部分内容是整个解析几何的基础，在解析几何的知识体系中占有重要位置，但由于在高中阶段平面解析几何的主要内容是圆锥曲线与方程，故该部分在高考考查的分值不多，在高考试卷中一般就是一个选择题或者填空题考查直线与方程、圆与方程的基本问题，偏向于考查直线与圆的综合，试题难度不大，对直线方程、圆的方程的深入考查则与圆锥曲线结合进行．2．圆锥曲线与方程是高考考查的核心内容之一，在高考中一般有1～2道选择题或者填空题，一道解答题．选择题或者填空题在于有针对性地考查椭圆、双曲线、抛物线的定义、标准方程和简单几何性质及其应用，试题考查主要针对圆锥曲线本身，综合性较小，试题的难度一般不大．解答题中主要是以椭圆、抛物线为基本依托，考查椭圆、抛物线方程的求解，考查直线与曲线的位置关系，考查数形结合思想、函数与方程思想、等价转化思想、分类与整合思想等数学思想方法，这道解答题往往是试卷的压轴题之一．在备考复习中，要注意以下的高考重点、热点和命题方向：(1)直线的方程命题重点：直线的倾斜角与斜率、两条直线的位置关系、对称及与其他知识结合考查距离等．(2)圆的方程命题重点：由所给条件求圆的方程、直线与圆的位置关系．(3)圆锥曲线常通过客观题考查圆锥曲线的基本量(定义、性质)，通过大题考查直线与圆锥曲线的位置关系，求曲线的方程等．(4)在知识的交汇处命题是解析几何的显著特征，与向量、三角函数、不等式、数列、导数、立体几何等知识结合，考查综合分析问题和解决问题的能力．根据近年广东高考对本章内容的考查情况， 预计该部分的考查仍然是以客观题考查直线与圆的基础知识和方法、圆锥曲线的定义和性质，以解答题考查直线与圆、直线与圆锥曲线的位置关系，以及将解析几何与其他数学知识相结合考查综合运用能力．学好本章的关键在于正确理解和掌握由曲线求方程和由方程讨论曲线的性质这两个问题．为此建议在复习备考中做到：1．搞清概念(对概念定义应“咬文嚼字”)；2．熟悉曲线(会“速写”出符合题目数量特征要求的曲线)；3．熟练运用代数、三角、几何、向量的知识；4．处理问题时要在“大处着眼”(即在整体上把握问题的综合信息和处理问题的数学思想)，“小处着手”(即在细节上能熟练运用各种数学知识和方法)．在具体复习过程中应要注意如下几点：1．要能分辨线段的有向与无向概念上的混淆，有向线段的数量与有向线段长度的混淆，能否分清这两点是学好有向线段的关键．2．在解答有关直线的问题时，要注意：(1)在确定直线的斜率、倾斜角时，首先要注意斜率存在的条件，其次是倾斜角的范围；(2)在利用直线的截距式解题时，要注意防止由于“零截距”而造成丢解的情况；(3)在利用直线的点斜式、斜截式解题时，要注意检验斜率不存在的情况，防止丢解；(4)要灵活运用中点坐标公式，在解决有关分割问题、对称问题时可以简化运算；(5)掌握对称问题的四种基本类型的解法；(6)在由两直线的位置关系确定有关参数的值或其范围时，要充分利用分类讨论、数形结合、特殊值检验等基本的数学思想方法．3．熟练掌握圆的标准方程与一般方程，能由方程迅速求出圆心坐标和半径，能结合运用圆的几何性质，会使解题难度降低且速度快捷．4．熟练掌握三类圆锥曲线的标准方程与几何性质，注意数形结合思想方法的运用．第七章 平面解析几何第一节 直线的斜率与直线方程知识梳理一、直线的倾斜角1．定义：在平面直角坐标系中，对于一条与x 轴相交的直线l ，如果把x 轴绕着交点1.在平面直角坐标系中，结合具体图形，确定直线位置的几何要素．2.理解直线的倾斜角和斜率的概念，掌握过两点的直线斜率的计算公式．3.掌握确定直线位置的几何要素，掌握直线方程的几种形式(点斜式、两点式及一般式)，了解斜截式与一次函数的关系．按________________到和________时所转的________记为α，那么α就叫做直线的倾斜角．当直线l 与x 轴重合或平行时，规定倾斜角为0.2．倾斜角的取值范围： ________.答案：1.逆时针方向转 直线l 重合 最小正角2.[0，π]二、直线的斜率1．定义：倾斜角不是90°的直线，它的倾斜角的正切值叫做这条直线的斜率k ，即k ＝tan α(α≠90°)；倾斜角为________的直线没有斜率．2．斜率公式：经过P 1(x 1，y 1)，P 2(x 2，y 2)两点的直线的斜率为__________________．答案：1.90°2. k =y 1-y 2x 1-x 2（x 1≠x 2）三、求直线斜率的方法1．定义法：已知直线的倾斜角为α，且α≠90°，则斜率k ＝tan α.2.公式法：已知直线过P 1(x 1，y 1)，P 2(x 2，y 2)两点，且x 1≠x 2，则斜率k ＝y 2－y 1x 2－x 1. 四、斜率的应用：证明三点共线： kAB ＝kBC.五、直线方程的几种形式基础自测1．已知直线l 经过第二、四象限，且与y 轴正方向的夹角为30°，则直线l 的斜率是( )A. 3 B ．－ 3 C ．－33 D.33解析：经过作图易知直线l 的倾斜角为120°，则斜率k ＝tan 120°＝－3，故选B .答案：B2．直线x ＋(a 2＋1)y ＋1＝0(a ∈R )的倾斜角的取值范围是( )A.⎣⎢⎡⎦⎥⎤0，π4B.⎣⎢⎡⎭⎪⎫3π4，πC.⎣⎢⎡⎦⎥⎤0，π4∪⎝ ⎛⎭⎪⎫π2，πD.⎣⎢⎡⎭⎪⎫π4，π2∪⎣⎢⎡⎭⎪⎫3π4，π解析：斜率k ＝－1a 2＋1，故k∈[－1,0)．由正切函数图象知，倾斜角α∈⎣⎢⎡⎭⎪⎫3π4，π.故选B .答案：B3．已知直线l 的斜率为3，在y 轴上截距为另一条直线x －2y －4＝0的斜率的倒数，则直线l 的方程为______________．解析：因为x －2y －4＝0的斜率为12，所以直线l 在y 轴上截距为2，所以直线l 的方程为y ＝3x ＋2.答案：y ＝3x ＋24．已知两点A (－1，－5)，B (3，－2)，若直线l 过点(1,2)且直线l 的倾斜角是直线AB 倾斜角的一半，则直线l 的方程是__________________.答案：x －3y ＋5＝01．曲线y ＝x 3－2x ＋1在点(1,0)处的切线方程为( )A ．y ＝x －1B ．y ＝－x ＋1C ．y ＝2x －2D ．y ＝－2x ＋2解析：切线的斜率k ＝f′(1)＝(3x 2－2)|x ＝1＝1，根据点斜式得切线方程为y ＝x －1.故选A .答案：A2．在平面直角坐标系中，如果x 与y 都是整数，就称点(x ，y )为整点．下列命题中正确的是________(写出所有正确命题的编号)．①存在这样的直线，既不与坐标轴平行又不经过任何整点 ②如果k 与b 都是无理数，则直线y ＝kx ＋b 不经过任何整点 ③直线l 经过无穷多个整点，当且仅当l 经过两个不同的整点 ④直线y ＝kx ＋b 经过无穷多个整点的充要条件是：k 与b 都是有理数 ⑤存在恰经过一个整点的直线解析：①正确．比如直线y ＝2x ＋3，不与坐标轴平行，且当x 取整数时，y 始终是一个无理数，即不经过任何整点；②错误．直线y ＝3x －3中k 与b 都是无理数，但直线经过整点(1,0)．③正确．当直线经过两个整点时，它经过无数多个整点．④错误．当k ＝0，b ＝13时，直线y ＝13不通过任何整点．⑤正确．比如直线y ＝3x －3只经过一个整点(1,0)． 答案：①③⑤1．(2013·太原模拟)设A 、B 是x 轴上的两点，点P 的横坐标为3，且|PA |＝|PB |，若直线PA 的方程为x －y ＋1＝0，则直线PB 的方程是( )A ．x ＋y －5＝0B ．2x －y －1＝0C ．x －2y ＋4＝0D ．x ＋y －7＝0解析：由|PA|＝|PB|知点P 在AB 的垂直平分线上．由点P 的横坐标为3，且PA 的方程为x －y ＋1＝0，得P(3,4)．直线PA 、PB 关于直线x ＝3对称，直线PA 上的点(0,1)关于直线x ＝3的对称点(6,1)在直线PB 上，所以直线PB 的方程为x ＋y －7＝0.答案：D2．(2013·湖北孝感统考)直线x ＋a 2y －a ＝0(a >0，a 是常数)，当此直线在x ，y 轴上的截距和最小时，a 的值是________．解析：方程可化为x a ＋y 1a＝1，因为a>0，所以截距之和t ＝a ＋1a ≥2，当且仅当a ＝1a，即a ＝1时取等号．答案：1。

第四节 直线与圆、圆与圆的位置关系知识梳理一、点与圆的位置关系若圆(x －a )2＋(y －b ) 2＝r 2，那么点(x 0，y 0)在 圆上⇔____________________________________； 圆外⇔____________________________________； 圆内⇔____________________________________.答案：（x 0-a ）2+(y 0-b)2=r 2 （x 0-a ）2+(y 0-b)2＞r 2（x 0-a ）2+(y 0-b)2＜r 2二、直线与圆的位置关系直线与圆有三种位置关系：相离、相切和相交．有两种判断方法： 1．代数法(判别式法)．Δ>0⇔________；Δ＝0⇔________；Δ<0⇔________.2．几何法：圆心到直线的距离⎩⎪⎨⎪⎧d <r ⇔ ；d ＝r ⇔ ；d >r ⇔ .一般宜用几何法．答案：1.相交 相切 相离 2.相交 相切 相离三、圆与圆的位置关系：相离，外切，相交，内切，内含 设圆O 1与圆O 2的半径分别为r 1和r 2，于是有 1.||O 1O 2>r 1＋r 2⇔相离． 2.||O 1O 2＝r 1＋r 2⇔外切．3.||r 1－r 2<||O 1O 2<r 1＋r 2⇔相交．4.||O 1O 2＝||r 1－r 2⇔内切．5.||O 1O 2<||r 1－r 2⇔内含． 四、弦长求法一般采用几何法：弦心距d ，圆半径r ，弦长l ，则d 2＋⎝ ⎛⎭⎪⎫l 22＝r 2. 基础自测1.能根据给定直线、圆的方程，判断直线与圆的位置关系.能根据给定两个圆的方程判断两个圆的位置关系.2.能用直线和圆的方程解决一些简单的问题.3.初步了解代数方法处理几何问题的思想.1．直线y ＝kx ＋2与圆：x 2＋y 2＝1没有公共点的充要条件是( ) A ．k ∈(－2，2) B ．k ∈(－3，3)C ．k ∈(－∞，－2)∪(2，＋∞)D ．k ∈(－∞，－3)∪(3，＋∞)解析：由圆心到直线的距离公式可得d ＝|2|1＋k2>1，解得－3<k <3，故选B. 答案：B2．过点A (a ，a )可作圆x 2＋y 2－2ax ＋a 2＋2a －3＝0的两条切线，则实数a 的取值范围为( )A ．(－∞，－3)∪⎝ ⎛⎭⎪⎫1，32 B.⎝ ⎛⎭⎪⎫1，32 C ．(－∞，－3) D ．(－3,1)∪⎝ ⎛⎭⎪⎫32，＋∞解析：已知圆的圆心为C (a,0)，半径为r ＝3－2a .依题意有|AC |＞r ，即|a |＞3－2a ，∴a 2＞3－2a 且3－2a ＞0，解得a ＜－3或1＜a ＜32.故选A.答案：A3．过原点的直线与圆x 2＋y 2－2x －4y ＋4＝0相交所得弦的长为2，则该直线的方程为____________．解析：圆的方程化为标准形式为(x －1)2＋(y －2)2＝1，又相交所得弦长为2，故相交弦为圆的直径，由此得直线过圆心(1,2)，故所求直线方程为2x －y ＝0.答案：2x －y ＝04．如图，已知直线l ：x －y ＋4＝0与圆C ：()x －12＋()y －12＝2，则圆C 上各点到l 的距离的最小值为________．解析：由题图可知：过圆心作直线l ：x －y ＋4＝0的垂线，则AD 长即为所求．∵C ：()x －12＋()y －12＝2的圆心为C ()1，1，半径为2，点C 到直线l ：x －y ＋4＝0的距离为d ＝||1－1＋42＝22，∴|AD |＝|CD |－|AC |＝22－2＝2，故C 上各点到l 的距离的最小值为 2.答案： 21．(2012·天津卷)设m ，n ∈R ，若直线(m ＋1)x ＋(n ＋1)y －2＝0与圆(x －1)2＋(y －1)2＝1相切，则m ＋n 的取值范围是( )A ．[1－3，1＋3]B ．(－∞，1－3]∪[1＋3，＋∞)C ．[2－22，2＋22]D ．(－∞，2－22]∪[2＋22，＋∞)解析：∵直线(m ＋1)x ＋(n ＋1)y －2＝0与圆(x －1)2＋(y －1)2＝1相切，∴圆心(1,1)到直线的距离为d ＝m ＋＋n ＋－2|m ＋2＋n ＋12＝1，∴mn ＝m ＋n ＋1≤⎝ ⎛⎭⎪⎫m ＋n 22.设t ＝m ＋n ，则14t 2≥t ＋1，解得t ∈(－∞，2－22]∪[2＋22，＋∞)．故选D. 答案：D2．(2013·江苏卷)如图，在平面直角坐标系xOy 中，点A (0,3)，直线l ：y ＝ 2x －4.设圆的半径为1，圆心在l 上．(1)若圆心C 也在直线y ＝x －1上，过点A 作圆C 的切线，求切线的方程； (2)若圆C 上存在点M ，使MA ＝2MO ，求圆心C 的横坐标a 的取值范围．解析：(1)由y ＝2x －4，y ＝x －1联立方程组，解得圆心坐标C (3,2)，所以圆方程为(x －3)2＋(y －2)2＝1， 因为切线斜率不存在时，不合题意， 所以设切线方程为y ＝kx ＋3，所以|3k －2＋3|1＋k2＝1，解得k ＝0或k ＝－34， 所以切线方程为y ＝3或y ＝－34x ＋3.(2)设C (a,2a －4)，则圆方程为(x －a )2＋(y －2a ＋4)2＝1，设M (x 0，y 0)，由题意(x 0－a )2＋(y 0－2a ＋4)2＝1，因为MA ＝2MO ，所以x 20＋(y 0－3)2＝4x 20＋4y 20，即x 20＋(y 0＋1)2＝4， 因为点M 存在，所以圆(x －a )2＋(y －2a ＋4)2＝1与圆x 2＋(y ＋1)2＝4有公共点，即两圆相交或相切，所以(2－1)2≤d 2≤(2＋1)2，即1≤(a －0)2＋[2a －4－(－1) ]2≤9，即a 的取值范围为⎣⎢⎡⎦⎥⎤0，125.1．已知圆C ： x 2＋y 2－2x ＋4y －4＝0，直线l ：2x ＋y ＝0，则圆C 上的点到直线l 的距离最大值为( )A ．1B ．2C ．3D ．4解析：直线l ：2x ＋y ＝0是确定的，圆上的动点到直线的距离的最大值为圆心到直线的距离加上圆的半径．圆的圆心为(1，－2)，半径为3，因为点(1，－2)在直线l ：2x ＋y ＝0上，所以，最大距离为圆的半径3.故选C.答案：C2．(2013·江门一模)已知x 、y 满足x 2＋y 2＝4，则z ＝3x －4y ＋5的取值范围是( ) A ．[－5,15] B ．[－10,10] C ．[－2,2] D ．[0,3]解析：z ＝3x －4y ＋5 即直线 3x －4y ＋5－z ＝0，由题意可得直线和圆 x 2＋y 2＝4有交点，故有|0－0＋5－z |9＋16≤2，化简可得－10≤z －5≤10，解得－5≤z ≤15，故选A.答案：A。

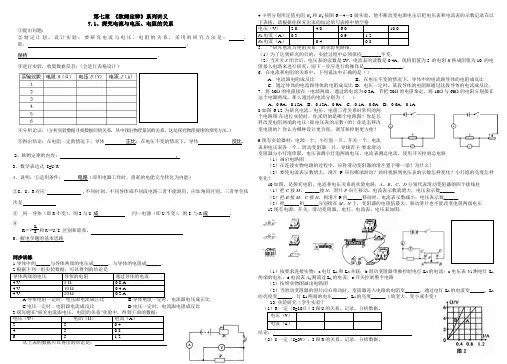
第七章《欧姆定律》系列讲义7.1、探究电流与电压、电阻的关系①提出问题：②制定计划，设计实验：要研究电流与电压、电阻的关系，采用的研究方法是：。

即：；保持。

③进行实验，收集数据信息：（会进行表格设计）④分析论证：（分析实验数据寻找数据间的关系，从中找出物理量间的关系，这是探究物理规律的常用方法。

）⑤得出结论：在电阻一定的情况下，导体正比；在电压不变的情况下，导体反比。

2、欧姆定律的内容：。

3、数学表达式 I=U/R4、说明：①适用条件：电路（即用电器工作时，消耗的电能完全转化为内能）②I、U、R对应，不同时刻、不同导体或不同段电路三者不能混用，应加角码区别。

三者单位依次是③同一导体（即R不变），则I与U 成同一电源（即U不变），则I 与R成。

④R＝U/I 区别和联系。

5、解电学题的基本思路同步训练1.导体中的______与导体两端的电压成______，与导体的电阻成______。

C.电压一定时，电阻跟电流成反比D.电压一定时，电流跟电阻成反比从上表的数据可以得出的结论是：.4.小明分别用定值电阻R1和R2按图6－4－8做实验，他不断改变电源电压后把电压表和电流表的示数记录在以下表格，请根据你探究出来的结论填写表格中的5．“研究电流与电阻关系”的实验电路图．（1）为了达到研究的目的，实验过程中必须保持________不变．（2）当开关S闭合后，电压表的读数是2V，电流表的读数是0.4A．现将阻值为5 的电阻R换成阻值为10的电阻接入电路来进行研究，则下一步应进行的操作是________________．6．在电流和电阻的关系中，下列说法中正确的是（）．A．电流跟电阻成反比B．在电压不变的情况下，导体中的电流跟导体的电阻成反比C．通过导体的电流跟导体的电阻成反比D．电压一定时，某段导体的电阻跟通过这段导体的电流成反比．7．将30Ω的电阻接在一电源两端，通过的电流为0.3A．若把30Ω的电阻拿走，将10Ω与60Ω的电阻分别接在这个电源两端，那么通过的电流分别为（）A．0.9A，0.15A B．0.15A，0.9A C．0.1A，0.6A D．0.6A，0.1A8.如图6-12为研究电流、电压、电阻三者关系时常用的两个电路图.在进行实验时，你采用的是哪个电路图？你是怎样改变电阻两端的电压（即电压表的示数）的？你是怎样改变电阻的？你认为哪种设计更合理、调节和控制更方便？9.现有实验器材：电源一个、小灯泡一只、开关一个、电流表和电压表各一个、滑动变阻器一只、导线若干.要求滑动变阻器与小灯泡串联，电压表测小灯泡两端电压，电流表测总电流，使用开关控制总电路.（1）画出电路图.（2）在连接实物电路的过程中，应将滑动变阻器的滑片置于哪一端？为什么？（3）要使电流表示数增大，滑片P应向哪端滑动？此时观察到电压表的示数怎样变化？小灯泡的亮度怎样变化？10.如图，是探究电阻、电流和电压关系的实验电路，A、B、C、D分别代表滑动变阻器的四个接线柱.（1）把C接M，______接N，滑片P向左移动，电流表示数就增大，电压表示数______.（2）把B接M，C接N，则滑片P向______移动时，电流表示数减小，电压表示数______.（3）把______和______分别接在M、N上，变阻器的电阻值最大，移动滑片也不能改变电阻两端电压.12.现有电源、开关、滑动变阻器、电灯、电流表、电压表如图：（1）按要求连接实物：a.电灯L1和L2并联；b.滑动变阻器单独控制电灯L2的电流；c.电压表V1测电灯L1两端的电压；d.电流表A2测流过L2的电流；e.开关控制整个电路.（2）按照实物图画出电路图.（3）当滑动变阻器的滑片向右移动时，变阻器连入电路的电阻变______，通过电灯L2的电流变______，L2的亮度变______，灯L1两端的电压______，L1的亮度______（填变大、变小或不变）.13 实验研究（学生实验）结论：结论：（3）综合（1）（2）结论可得出电流、电压、电阻的关系表达式为：_ _；（4）本实验采用的研究方法是_____。

第9节实验：验证机械能守恒定律一、实验目的1．会用打点计时器打下的纸带计算物体运动的速度。

2．掌握利用自由落体运动验证机械能守恒定律的原理和方法。

二、实验原理让物体自由下落，忽略阻力情况下物体的机械能守恒，有两种方案验证物体的机械能守恒：1．以物体下落的起始点O 为基准，测出物体下落高度h 时的速度大小v ，若12mv 2＝mgh 成立，则可验证物体的机械能守恒。

2．测出物体下落高度h 过程的初、末时刻的速度v 1、v 2，若关系式12mv 22－12mv 12＝mgh 成立，则物体的机械能守恒。

三、实验器材铁架台(带铁夹)、电磁打点计时器、重锤(带纸带夹子)、纸带、复写纸、导线、毫米刻度尺、低压交流电源。

四、实验步骤1．安装置：按图将检查、调整好的打点计时器竖直固定在铁架台上，接好电路。

2．打纸带：将纸带的一端用夹子固定在重物上，另一端穿过打点计时器的限位孔，用手提着纸带使重物静止在靠近打点计时器的地方。

先接通电源，后松开纸带，让重物带着纸带自由下落。

更换纸带重复做3次～5次实验。

3．选纸带：选取点迹较为清晰且有两点间的距离约为2 mm 的纸带，把纸带上打出的两点间的距离为2 mm 的第一个点作为起始点，记作O ，在距离O 点较远处再依次选出计数点1、2、3…4．测距离：用刻度尺测出O 点到1、2、3…的距离，即为对应下落的高度h 1、h 2、h 3… 五、数据处理1．计算各点对应的瞬时速度：记下第1个点的位置O ，在纸带上从离O 点适当距离开始选取几个计数点1、2、3…并测量出各计数点到O 点的距离h 1、h 2、h 3…再根据公式v n ＝h n ＋1－h n －12T，计算出1、2、3、4、…n 点的瞬时速度v 1、v 2、v 3、v 4、…v n 。

2．机械能守恒验证方法一：利用起始点和第n 点。

从起始点到第n 个计数点，重力势能减少量为mgh n ，动能增加量为12mv n 2，计算gh n 和12v n 2，如果在实验误差允许的X 围内gh n ＝12v n 2，则机械能守恒定律得到验证。

实验九练习使用多用电表一、电流表与电压表的改装1．改装方案改装为电压表改装为大量程的电流表原理串联电阻分压并联电阻分流改装原理图分压电阻或分流电阻U＝I g（R g＋R）故R＝UI g－R gI g R g＝(I－I g）R故R＝错误!改装后电表内阻R V＝R g＋R〉R g R A＝错误!<R g2。

校正(1）电压表的校正电路如图1所示,电流表的校正电路如图2所示．图1图2(2)校正的过程是：先将滑动变阻器的滑动触头移到最左端，然后闭合开关，移动滑动触头，使改装后的电压表（电流表)示数从零逐渐增大到量程值，每移动一次记下改装的电压表(电流表）和标准电压表（标准电流表）示数，并计算满刻度时的百分误差,然后加以校正．二、欧姆表原理（多用电表测电阻原理)1．构造：如图3所示,欧姆表由电流表G、电池、调零电阻R和红、黑表笔组成．图3欧姆表内部：电流表、电池、调零电阻串联．外部:接被测电阻R x。

全电路电阻R总＝R g＋R＋r＋R x。

2．工作原理：闭合电路欧姆定律，I＝错误!.3．刻度的标定：红、黑表笔短接(被测电阻R x＝0)时，调节调零电阻R,使I＝I g,电流表的指针达到满偏，这一过程叫欧姆调零．(1）当I＝I g时，R x＝0,在满偏电流I g处标为“0"．（图甲）(2)当I＝0时，R x→∞,在I＝0处标为“∞”．（图乙）（3)当I＝错误!时，R x＝R g＋R＋r,此电阻值等于欧姆表的内阻值，R x 叫中值电阻．三、多用电表1．多用电表可以用来测量电流、电压、电阻等,并且每一种测量都有几个量程．2．外形如图4所示：上半部为表盘，表盘上有电流、电压、电阻等多种量程的刻度；下半部为选择开关，它的四周刻有各种测量项目和量程．图43．多用电表面板上还有:欧姆表的欧姆调零旋钮（使电表指针指在右端零欧姆处)、指针定位螺丝（使电表指针指在左端的“0”位置）、表笔的正、负插孔（红表笔插入“＋”插孔，黑表笔插入“－”插孔)．四、二极管的单向导电性1．晶体二极管是由半导体材料制成的，它有两个极，即正极和负极，它的符号如图5甲所示．图52．晶体二极管具有单向导电性(符号上的箭头表示允许电流通过的方向)．当给二极管加正向电压时,它的电阻很小，电路导通，如图乙所示；当给二极管加反向电压时，它的电阻很大,电路截止，如图丙所示．3．将多用电表的选择开关拨到欧姆挡，红、黑表笔接到二极管的两极上，当黑表笔接“正"极，红表笔接“负”极时，电阻示数较小，反之电阻示数很大，由此可判断出二极管的正、负极．1．实验器材多用电表、电学黑箱、直流电源、开关、导线若干、小灯泡、二极管、定值电阻（大、中、小）三个．2．实验步骤（1）观察:观察多用电表的外形，认识选择开关的测量项目及量程．(2）机械调零：检查多用电表的指针是否停在表盘刻度左端的零位置．若不指零,则可用小螺丝刀进行机械调零．（3）将红、黑表笔分别插入“＋”、“－”插孔．（4）测量小灯泡的电压和电流．①按如图6甲所示的电路图连好电路，将多用电表选择开关置于直流电压挡，测小灯泡两端的电压．图6②按如图乙所示的电路图连好电路，将选择开关置于直流电流挡，测量通过小灯泡的电流．(5)测量定值电阻①根据被测电阻的估计阻值，选择合适的挡位,把两表笔短接，观察指针是否指在欧姆表的“0”刻度，若不指在欧姆表的“0”刻度，调节欧姆调零旋钮,使指针指在欧姆表的“0"刻度处；②将被测电阻接在两表笔之间,待指针稳定后读数；③读出指针在刻度盘上所指的数值,用读数乘以所选挡位的倍率，即得测量结果；④测量完毕,将选择开关置于交流电压最高挡或“OFF”挡．1．多用电表使用注意事项（1)表内电源正极接黑表笔，负极接红表笔，但是红表笔插入“＋”插孔,黑表笔插入“－”插孔，注意电流的实际方向应为“红入"，“黑出"．（2）区分“机械零点"与“欧姆零点"．机械零点是表盘刻度左侧的“0”位置，调整的是表盘下边中间的指针定位螺丝;欧姆零点是指刻度盘右侧的“0”位置，调整的是欧姆调零旋钮．(3）由于欧姆挡表盘难以估读，测量结果只需取两位有效数字,读数时注意乘以相应挡位的倍率．(4)使用多用电表时，手不能接触表笔的金属杆,特别是在测电阻时，更应注意不要用手接触表笔的金属杆．(5）测量电阻时待测电阻要与其他元件和电源断开，否则不但影响测量结果，甚至可能损坏电表．(6)测电阻时每换一挡必须重新欧姆调零．(7)使用完毕，选择开关要置于交流电压最高挡或“OFF”挡．长期不用，应把表内电池取出．2．多用电表对电路故障的检测（1)断路故障的检测方法①用直流电压挡：a．将电压表与电源并联，若电压表示数不为零,说明电源良好，若电压表示数为零，说明电源损坏．b．在电源完好时，再将电压表与外电路的各部分电路并联．若电压表示数等于电源电动势,则说明该部分电路中有断点．②用直流电流挡:将电流表串联在电路中,若电流表的示数为零，则说明与电流表串联的部分电路断路．③用欧姆挡检测将各元件与电源断开，然后接到红、黑表笔间，若有阻值（或有电流）说明元件完好，若电阻无穷大(或无电流)说明此元件断路．（2)短路故障的检测方法①将电压表与电源并联，若电压表示数为零，说明电源被短路;若电压表示数不为零，则外电路的部分电路不被短路或不完全被短路．②用电流表检测,若串联在电路中的电流表示数不为零，故障应是短路．命题点一教材原型实验例1在“练习使用多用电表"的实验中：图7(1)某同学用多用电表测量电阻，电路如图7甲所示,若选择开关置于“×100”挡，按正确使用方法测量电阻R x的阻值,指针位于图乙所示位置，则R x＝________ Ω。

§7.7向量法求空间角课标要求 1.能用向量法解决异面直线所成角、直线与平面所成角、平面与平面的夹角问题，并能描述解决这一类问题的程序，体会向量法在研究空间角问题中的作用.2.弄清折叠问题中的变量与不变量，掌握折叠问题中线面位置关系的判断和空间角的计算问题．知识梳理1．异面直线所成的角若异面直线l 1，l 2所成的角为θ，其方向向量分别是u ，v ，则cos θ＝|cos 〈u ，v 〉|＝|u·v ||u||v |.2．直线与平面所成的角如图，直线AB 与平面α相交于点B ，设直线AB 与平面α所成的角为θ，直线AB 的方向向量为u ，平面α的法向量为n ，则sin θ＝|cos 〈u ，n 〉|＝|u ·n |u ||n ||＝|u·n||u||n|.3．平面与平面的夹角如图，平面α与平面β相交，形成四个二面角，我们把这四个二面角中不大于90°的二面角称为平面α与平面β的夹角．若平面α，β的法向量分别是n 1和n 2，则平面α与平面β的夹角即为向量n 1和n 2的夹角或其补角．设平面α与平面β的夹角为θ，则cos θ＝|cos 〈n 1，n 2〉|＝|n 1·n 2||n 1||n 2|.常用结论1．异面直线所成角的范围是，π2；直线与平面所成角的范围是0，π2；二面角的范围是[0，π]，两个平面夹角的范围是0，π2.2．若平面α与平面β的夹角为θ1，平面α内的直线l 与平面β所成角为θ2，则θ1≥θ2，当l 与α和β的交线垂直时，取等号．自主诊断1．判断下列结论是否正确．(请在括号中打“√”或“×”)(1)两直线的方向向量所成的角就是两条直线所成的角．(×)(2)直线的方向向量和平面的法向量所成的角就是直线与平面所成的角．(×)(3)二面角的平面角为θ，则两个平面的法向量的夹角也是θ.(×)(4)二面角α－l －β的平面角与平面α，β的夹角相等．(×)2．已知向量m ，n 分别是直线l 和平面α的方向向量和法向量，若cos 〈m ，n 〉＝－12，则直线l 与平面α所成的角为()A ．30°B ．60°C ．120°D ．150°答案A 解析设直线l 与平面α所成的角为θ，则sin θ＝|cos 〈m ，n 〉|＝12，所以直线l 与平面α所成的角为30°.3．已知直线l 1的方向向量s 1＝(1,0,1)与直线l 2的方向向量s 2＝(－1,2，－2)，则直线l 1和l 2所成角的余弦值为()A.24 B.12 C.22 D.32答案C解析设直线l 1与l 2所成的角为θ，因为s 1＝(1,0,1)，s 2＝(－1,2，－2)，所以cos θ＝|cos 〈s 1，s 2〉|＝|s 1·s 2||s 1||s 2|＝|－1－2|2×3＝22.所以直线l 1和l 2所成角的余弦值为22.4．已知两平面的法向量分别为m ＝(0,1,0)，n ＝(0,1,1)，则两平面所成的二面角为()A.π4B.3π4C.π4或3π4D.π2或3π4答案C 解析∵m ＝(0,1,0)，n ＝(0,1,1)，∴m ·n ＝1，|m |＝1，|n |＝2，若两平面所成的二面角为θ，则|cos θ|＝|cos 〈m ，n 〉|＝|m ·n ||m ||n |＝22，∴两平面所成的二面角为π4或3π4.题型一异面直线所成的角例1(1)(2023·武汉模拟)如图，在四棱锥P －ABCD 中，PA ⊥底面ABCD ，底面ABCD 为正方形，PA ＝BC ，E 为CD 的中点，F 为PC 的中点，则异面直线BF 与PE 所成角的余弦值为()A ．－39 B.39C ．－539 D.539答案B 解析如图，以点A 为坐标原点，以AB ，AD ，AP 所在直线分别为x 轴、y 轴、z 轴，建立空间直角坐标系，设AB ＝2，异面直线BF 与PE 所成的角为θ，则A (0,0,0)，B (2,0,0)，P (0,0,2)，C (2,2,0)，D (0,2,0)，则E (1,2,0)，F (1,1,1)，所以BF →＝(－1,1,1)，PE →＝(1,2，－2)，所以cos θ＝|cos 〈BF →，PE →〉|＝|BF →·PE →||BF →||PE →|＝|－1＋2－2|3×3＝39，所以异面直线BF 与PE 所成角的余弦值为39.(2)(2023·开封模拟)在如图所示的圆台中，四边形ABCD 为其轴截面，AB ＝2CD ＝4，母线长为3，P 为下底面圆周上一点，异面直线AD 与OP (O 为下底面圆心)所成的角为π3，则CP 2的大小为()A ．7－23B ．7－23或7＋23C ．19－43D ．19－43或19＋43答案B 解析以O 为原点，OB 所在直线为y 轴，过点O 作x 轴⊥OB ，圆台的轴为z 轴，建立如图所示的空间直角坐标系，作DE ⊥AB 于点E ，AE ＝12AB －12CD ＝1，在Rt △ADE 中，AD ＝3，DE ＝AD 2－AE 2＝2，则D (0，－1，2)，A (0，－2,0)，C (0,1，2)，AD →＝(0,1，2)，设P (2cos θ，2sin θ，0)，0≤θ<2π，OP →＝(2cos θ，2sin θ，0)，由于异面直线AD 与OP (O 为下底面圆心)所成的角为π3，∴cos π3＝|OP →·AD →||OP →||AD →|＝|2sin θ|2×3＝|sin θ|3＝12，∴sin θ＝±32，CP →＝(2cos θ，2sin θ－1，－2)，CP 2＝|CP →|2＝4cos 2θ＋4sin 2θ－4sin θ＋1＋2＝7－4sin θ＝7±23.思维升华用向量法求异面直线所成的角的一般步骤(1)建立空间直角坐标系．(2)用坐标表示异面直线的方向向量．(3)利用向量的夹角公式求出向量夹角的余弦值．(4)，π2，即异面直线所成角的余弦值等于两向量夹角的余弦值的绝对值．跟踪训练1(1)(2023·台州统考)如图，已知菱形ABCD 的边长为3，对角线BD 长为5，将△ABD 沿着对角线BD 翻折至△A ′BD ，使得线段A ′C 长为3，则异面直线A ′B 与CD 所成角的余弦值为()A.34B.54C.49D.89答案D 解析因为A ′C ＝A ′D ＝CD ＝3.所以2A ′C ——→·CD →＝(A ′C ——→＋CD →)2－A ′C ——→2－CD →2＝A ′D ——→2－A ′C ——→2－CD →2＝9－9－9＝－9.因为CB ＝CD ＝3，BD ＝5.所以2CB →·CD →＝CB →2＋CD →2－(CB →－CD →)2＝CB →2＋CD →2－DB →2＝9＋9－25＝－7.所以A ′B ——→·CD →＝(A ′C ——→＋CB →)·CD →＝A ′C ——→·CD →＋CB →·CD →＝－92－72＝－8.若异面直线A ′B 与CD 所成的角为θ，则cos θ＝|cos 〈A ′B ——→，CD →〉|＝|A ′B ——→·CD →||A ′B ——→||CD →|＝|－8|3×3＝89.所以异面直线A ′B 与CD 所成角的余弦值为89.(2)如图所示，在棱长为2的正方体ABCD －A 1B 1C 1D 1中，E 是棱CC 1的中点，AF →＝λAD →(0<λ<1)，若异面直线D 1E 和A 1F 所成角的余弦值为3210，则λ的值为______．答案13解析以D 为坐标原点，DA ，DC ，DD 1所在直线分别为x 轴、y 轴、z 轴，建立空间直角坐标系(图略)，正方体的棱长为2，则A 1(2,0,2)，D 1(0,0,2)，E (0,2,1)，A (2,0,0)，∴D 1E —→＝(0,2，－1)，A 1A ＝(0,0，－2)，AD →＝(－2,0,0)，A 1F —→＝A 1A —→＋AF →＝A 1A —→＋λAD →＝(－2λ，0，－2)．∴|cos 〈A 1F —→，D 1E —→〉|＝|A 1F —→·D 1E —→||A 1F —→||D 1E —→|＝22λ2＋1×5＝3210，解得λ＝－13舍去题型二直线与平面所成的角例2(2022·全国甲卷)在四棱锥P －ABCD 中，PD ⊥底面ABCD ，CD ∥AB ，AD ＝DC ＝CB ＝1，AB ＝2，DP ＝3.(1)证明：BD ⊥PA ；(2)求PD 与平面PAB 所成的角的正弦值．(1)证明在四边形ABCD 中，作DE ⊥AB 于点E ，CF ⊥AB 于点F ，如图．因为CD ∥AB ，AD ＝CD ＝CB ＝1，AB ＝2，所以四边形ABCD 为等腰梯形，所以AE ＝BF ＝12，故DE ＝AD 2－AE 2＝32，BD ＝DE 2＋BE 2＝3，所以AD 2＋BD 2＝AB 2，所以AD ⊥BD .因为PD ⊥平面ABCD ，BD ⊂平面ABCD ，所以PD ⊥BD ，又PD ∩AD ＝D ，PD ，AD ⊂平面PAD ，所以BD ⊥平面PAD .又因为PA ⊂平面PAD ，所以BD ⊥PA .(2)解由(1)知，DA ，DB ，DP 两两垂直，如图，以D 为原点建立空间直角坐标系，则D (0,0,0)，A (1,0,0)，B (0，3，0)，P (0,0，3)，则AP →＝(－1,0，3)，BP →＝(0，－3，3)，DP →＝(0,0，3)．设平面PAB 的法向量为n ＝(x ，y ，z )，·AP →＝0，·BP →＝0，x ＋3z ＝0，－3y ＋3z ＝0，可取n ＝(3，1,1)，则cos 〈n ，DP →〉＝n ·DP →|n ||DP →|＝35×3＝55，所以PD 与平面PAB 所成角的正弦值为55.思维升华利用空间向量求线面角的解题步骤跟踪训练2(2023·开封模拟)如图，四边形ABCD 是圆柱OQ 的轴截面，圆柱OQ 的侧面积为63π，点P 在圆柱OQ 的下底面圆周上，且△OPB 是边长为3的等边三角形．(1)若G 是DP 的中点，求证：AG ⊥BD ；(2)若DG →＝2GP →，求GB 与平面ABCD 所成角的正弦值．(1)证明设圆柱OQ 的底面半径为r ，高为h .因为△OPB 是边长为3的等边三角形，所以∠ABP ＝60°，r ＝ 3.因为圆柱OQ 的侧面积为63π，所以2πrh ＝63π，解得h ＝3.在下底面圆O 中，∠APB ＝90°，∠ABP ＝60°，所以AP ＝BP ·tan 60°＝3.因为DA ⊥平面APB ，所以DA ⊥BP ，DA ⊥AP .因为∠APB ＝90°，所以AP ⊥BP ，又AP ∩AD ＝A ，AP ，AD ⊂平面APD ，所以BP ⊥平面APD .因为AG ⊂平面APD ，所以BP ⊥AG .在△DAP 中，AD ＝AP ＝3，G 是DP 的中点，所以DP ⊥AG .又BP ∩DP ＝P ，BP ，DP ⊂平面BPD ，所以AG ⊥平面BPD .因为BD ⊂平面BPD ，所以AG ⊥BD .(2)解在下底面圆O 内过O 作Ox ⊥AB ，连接OQ .以O 为原点，Ox →，OB →，OQ →分别为x ，y ，z 轴正方向建立如图所示的空间直角坐标系．则B (0，3，0)，D (0，－3，3)，P 32，32，0因为DG →＝2GP →，设G 点坐标为(x 0，y 0，z 0)，则(x 0，y 0＋3，z 0－3)＝x 0，32－y 0，－z0＝0＋3＝y 0－3＝－2z 0，0＝1，0＝0，0＝1，所以G (1,0,1)，所以GB →＝(－1，3，－1)．显然，向量n ＝(1,0,0)是平面ABCD 的一个法向量．设GB 与平面ABCD 所成的角为θ，所以sin θ＝|cos 〈GB →，n 〉|＝|GB →·n ||GB →||n |＝55.所以GB 与平面ABCD 所成角的正弦值为55.题型三平面与平面的夹角例3(12分)(2023·全国乙卷)如图，三棱锥P －ABC 中，AB ⊥BC ，AB ＝2，BC ＝22，PB ＝PC ＝6，BP ，AP ，BC 的中点分别为D ，E ，O ，AD ＝5DO ，点F 在AC 上，BF ⊥AO .(1)证明：EF ∥平面ADO ；[切入点：由BF ⊥AO 找F 位置](2)证明：平面ADO ⊥平面BEF ；[切入点：证明AO ⊥平面BEF ](3)求二面角D －AO －C 的正弦值．[关键点：由AO ⊥BE 及PB 长求点P 坐标][思路分析](1)利用向量及BF →⊥AO →→F 为AC 中点→EF ∥OD(2)利用勾股定理→AO ⊥OD →AO ⊥平面BEF(3)建系设点P 坐标→由AO ⊥BE 及PB 长求点P 坐标→求法向量→求角(1)证明设AF ＝tAC ，则BF →＝BA →＋AF →＝(1－t )BA →＋tBC →，AO →＝－BA →＋12BC →，(1分)①处用BA →，BC →表示BF →，AO→因为BF ⊥AO ，(3分)②处利用⊥找点F 位置BF →⊥AO →找点F 位置又D ，E ，O 分别为PB ，PA ，BC 的中点，于是EF ∥PC ，DO ∥PC ，所以EF ∥DO ，又EF ⊄平面ADO ，DO ⊂平面ADO ，所以EF ∥平面ADO .(4分)(2)证明由(1)可知EF ∥DO ，由题意可得AO ＝AB 2＋OB 2＝6，DO ＝12PC ＝62，所以AD ＝5DO ＝302，因此DO 2＋AO 2＝AD 2＝152，则DO⊥AO ，(6分)③处利用勾股定理证明AO ⊥OD所以EF ⊥AO ，又AO ⊥BF ，BF ∩EF ＝F ，BF ，EF ⊂平面BEF ，则有AO ⊥平面BEF ，(7分)又AO ⊂平面ADO ，所以平面ADO ⊥平面BEF .(8分)(3)解如图，以B 为坐标原点，BA ，BC 所在直线分别为x ，y 轴，建立空间直角坐标系，则B (0,0,0)，A (2,0,0)，O (0，2，0)，AO →＝(－2，2，0)．因为PB ＝PC ，BC ＝22，所以设P (x ，2，z )，z >0，(9分)则BE →＝BA →＋AE →＝BA →＋12AP →＝(2,0,0)＋12(x －2，2，z )④处求BE →坐标由(2)得AO ⊥BE ，分)⑤处利用AO ⊥BE 及PB 长求点P 坐标由D 为PB 的中点，得－12，22，AD →－52，22，设平面DAO 的法向量为n 1＝(a ，b ，c )，1·AD →＝0，1·AO →＝0，－52a ＋22b ＋32c ＝0，2a ＋2b ＝0，得b ＝2a ，c ＝3a ，取a ＝1，则n 1＝(1，2，3)．易知平面CAO 的一个法向量为n 2＝(0,0,1)，(11分)设二面角D －AO －C 的大小为θ，则|cos θ|＝|cos 〈n 1，n 2〉|＝|n 1·n 2||n 1||n 2|＝36＝22，所以sin θ＝1－12＝22，⑥处利用向量法求两法向量夹角故二面角D －AO －C 的正弦值为22.(12分)利用法向量的方向判断二面角二面角的大小可以通过这两个面的法向量的夹角求得，它等于两法向量的夹角或其补角，法向量的方向指向内部的称为“进”入半平面；法向量的方向指向外部的称为穿“出”半平面；当法向量m ，n “一进一出”时，m ，n 的夹角就是二面角的大小；当法向量m ，n “同进同出”时，m ，n 的夹角就是二面角的补角．典例在长方体ABCD －A 1B 1C 1D 1中，AD ＝AA 1＝1，AB ＝2，点E 为棱AB 的中点，则二面角D 1－EC －D 的余弦值为________．答案63解析建立如图所示的空间直角坐标系，由AD ＝AA 1＝1，AB ＝2，得E (1,1,1)，C (0,2,1)，D 1(0,0,0)，则D 1E —→＝(1,1,1)，D 1C —→＝(0,2,1)，设平面D 1EC 的法向量为n ＝(x ，y ，z )，1E →·n ＝0，1C →·n ＝0，＋y ＋z ＝0，y ＋z ＝0，令z ＝－2，得n ＝(1,1，－2)，易知平面DEC 的法向量为m ＝(0,0,1)，则cos 〈m ，n 〉＝m ·n |m ||n |＝－26＝－63，由法向量的方向为同出，得二面角D 1－EC －D 的余弦值为63.思维升华利用空间向量计算平面与平面夹角大小的常用方法(1)找法向量：分别求出两个平面的法向量，然后通过两个平面的法向量的夹角得到平面与平面夹角的大小．(2)找与棱垂直的方向向量：分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量，然后通过这两个向量的夹角可得到平面与平面夹角的大小．跟踪训练3(2023·新高考全国Ⅱ改编)如图，三棱锥A －BCD 中，DA ＝DB ＝DC ，BD ⊥CD ，∠ADB ＝∠ADC ＝60°，E 为BC 的中点．(1)证明：BC ⊥DA ；(2)点F 满足EF →＝DA →，求平面DAB 与平面ABF 夹角的正弦值．(1)证明如图，连接AE ，DE ，因为E 为BC 的中点，DB ＝DC ，所以DE ⊥BC ，因为DA ＝DB ＝DC ，∠ADB ＝∠ADC ＝60°，所以△ACD 与△ABD 均为等边三角形，所以AC ＝AB ，从而AE ⊥BC ，又AE ∩DE ＝E ，AE ，DE ⊂平面ADE ，所以BC ⊥平面ADE ，而DA ⊂平面ADE ，所以BC ⊥DA .(2)解不妨设DA ＝DB ＝DC ＝2，因为BD ⊥CD ，所以BC ＝22，DE ＝AE ＝ 2.所以AE 2＋DE 2＝4＝AD 2，所以AE ⊥DE ，又AE ⊥BC ，DE ∩BC ＝E ，DE ，BC ⊂平面BCD ，所以AE ⊥平面BCD .以E 为原点，ED ，EB ，EA 所在直线分别为x ，y ，z 轴，建立空间直角坐标系，如图所示，则D (2，0,0)，A (0,0，2)，B (0，2，0)，E (0,0,0)，设平面DAB 与平面ABF 的法向量分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)，平面DAB 与平面ABF 的夹角为θ，而AB →＝(0，2，－2)，因为EF →＝DA →＝(－2，0，2)，所以F (－2，0，2)，则AF →＝(－2，0,0)．1·DA →＝0，1·AB →＝0，1＋2z 1＝0，－2z 1＝0，取x 1＝1，所以n 1＝(1,1,1)．2·AB →＝0，2·AF →＝0，－2z 2＝0，2＝0，取y 2＝1，所以n 2＝(0,1,1)，所以|cos θ|＝|n 1·n 2||n 1||n 2|＝23×2＝63，从而sin θ＝1－69＝33.所以平面DAB 与平面ABF 夹角的正弦值为33.课时精练一、单项选择题1.如图，在直三棱柱ABC －A 1B 1C 1中，AB ＝AC ＝AA 1＝2，BC ＝2，点D 为BC 的中点，则异面直线AD 与A 1C 所成的角为()A.π2B.π3C.π4D.π6答案B 解析由题意可知，AB ，AC ，AA 1两两互相垂直，以A 为坐标原点，AB ，AC ，AA 1所在直线分别为x 轴、y 轴、z 轴建立如图所示的空间直角坐标系，则A (0,0,0)，A 1(0,0，2)，C (0，2，0)，，22，∴AD →，22，A 1C —→＝(0，2，－2)，∴|cos 〈AD →，A 1C —→〉|＝|AD →·A 1C —→||AD →||A 1C —→|＝12，∴异面直线AD 与A 1C 所成的角为π3.2．在正三棱柱ABC －A 1B 1C 1中，AB ＝AA 1，则AC 1与平面BB 1C 1C 所成角的正弦值为()A.22 B.155 C.64 D.63答案C 解析建立如图所示的坐标系，设AB ＝2，则C 1(3，1,0)，A (0,0,2)，AC 1—→＝(3，1，－2)，易知平面BB 1C 1C 的一个法向量为n ＝(1,0,0)．设AC 1与平面BB 1C 1C 所成的角为θ，则sin θ＝|cos 〈AC 1—→，n 〉|＝|AC 1—→·n ||AC 1—→||n |＝322＝64.所以AC 1与平面BB 1C 1C 所成角的正弦值为64.3.如图，在正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是BB 1和DD 1的中点，则平面ECF 与平面ABCD 夹角的余弦值为()A.33B.63C.13D.23答案B 解析以点A 为坐标原点，AB →，AD →，AA 1—→的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，如图所示．设正方体的棱长为2，则A (0,0,0)，E (2,0,1)，F (0,2,1)，C (2,2,0)，∴CE →＝(0，－2,1)，CF →＝(－2,0,1)．设平面ECF 的法向量为n ＝(x ，y ，z )，·n ＝0，·n ＝0，2y ＋z ＝0，2x ＋z ＝0，取x ＝1，得n ＝(1,1,2)．易知m ＝(0,0,1)是平面ABCD 的一个法向量，设平面ECF 与平面ABCD 的夹角为θ.∴cos θ＝|cos 〈m ，n 〉|＝|m ·n ||m ||n |＝21×6＝63.∴平面ECF 与平面ABCD 夹角的余弦值为63.4．(2023·沧州模拟)在正方体ABCD －A 1B 1C 1D 1中，P 是C 1D 1的中点，则异面直线AP 与BA 1所成角的余弦值为()A.26 B.36 C.13 D.23答案A解析方法一设正方体的棱长为2，取CC 1的中点Q ，连接PQ ，AD 1，AC ，AQ ，∵P 是C 1D 1的中点，∴PQ ∥CD 1∥A 1B ，故∠APQ 就是AP 与BA 1所成的角(或其补角)，由勾股定理得AP ＝AQ ＝8＋1＝3，PQ ＝2，由余弦定理得cos ∠APQ ＝AP 2＋PQ 2－AQ 22AP ·PQ ＝9＋2－92×3×2＝26，故异面直线AP 与BA 1所成角的余弦值为26.方法二设正方体的棱长为2，以点D 为坐标原点，以DA ，DC ，DD 1所在直线分别为x ，y ，z 轴建立空间直角坐标系，如图所示，则A (2,0,0)，P (0,1,2)，A 1(2,0,2)，B (2,2,0)，AP →＝(－2,1,2)，BA 1—→＝(0，－2,2)，|cos 〈AP →，BA 1—→〉|＝|AP →·BA 1—→||AP →||BA 1—→|＝23×22＝26，故异面直线AP 与BA 1所成角的余弦值为26.5．(2024·郑州模拟)如图，已知AB 是圆柱底面圆的一条直径，OP 是圆柱的一条母线，C 为底面圆上一点，且AC ∥OB ，OP ＝AB ＝2OA ，则直线PC 与平面PAB 所成角的正弦值为()A.1010B.55C.110D.14答案A 解析∵AB 是圆柱底面圆的一条直径，∴∠AOB ＝90°，∠ACB ＝90°，∵OP ＝AB ＝2OA ，∴∠BAO ＝45°，∴OA ＝OB ，∵AC ∥OB ，∴∠OAC ＝90°，∴四边形OACB 为正方形，设AB ＝2，建立如图所示的空间直角坐标系，则A (2，0,0)，B (0，2，0)，P (0,0,2)，C (2，2，0)，AB →＝(－2，2，0)，AP →＝(－2，0,2)，设平面PAB 的法向量为n ＝(x ，y ，z )，·AB →＝0，·AP →＝0，－2x ＋2y ＝0，－2x ＋2z ＝0，取x ＝2，则n ＝(2，2，1)，又PC →＝(2，2，－2)，设直线PC 与平面PAB 所成的角为θ，∴sin θ＝|cos 〈n ，PC →〉|＝|n ·PC →||n ||PC →|＝25×22＝1010，∴直线PC 与平面PAB 所成角的正弦值为1010.6．(2023·杭州模拟)若正方形ABCD 的边长为a ，E ，F 分别为CD ，CB 的中点(如图1)，沿AE ，AF 将△ADE ，△ABF 折起，使得点B ，D 恰好重合于点P (如图2)，则直线PA 与平面PCE 所成角的正弦值为()A.22B.34 C.36 D.32答案A 解析由E ，F 分别是为CD ，CB 的中点，可得EF 2＝CE 2＋CF 2＝DE 2＋BF 2＝PE 2＋PF 2，则PE ⊥PF .由AD ⊥DE ，AB ⊥BF ，可得PA ⊥PE ，PA ⊥PF ，所以PA ，PF ，PE 两两互相垂直，以P 为坐标原点，PE ，PF ，PA 分别为坐标轴建立如图所示的空间直角坐标系，可得P (0,0,0)，0，，a 2，A (0,0，a )，设C (x ，y ，z )，由AC ＝2a ，CE ＝CF ＝a 2，＋y 2＋(z －a )2＝2a 2，＋z 2＝a 24，＋y 2＋z 2＝a 24，＝a 3，＝a 3，＝－a 3，即得，a 3，－所以可得PE →0，PC →，a 3，－设平面PCE 的法向量为n ＝(x ′，y ′，z ′)，·PC →＝ax ′3＋ay ′3－az ′3＝0，·PE →＝ax ′2＝0，令y ′＝1，则x ′＝0，z ′＝1，所以平面PCE 的一个法向量为n ＝(0,1,1)，又PA →＝(0,0，a )，设PA 与平面PCE 所成的角为θ，所以sin θ＝|cos 〈PA →，n 〉|＝|PA →·n ||PA →||n |＝a 2a ＝22.二、多项选择题7．三棱锥A －BCD 中，平面ABD 与平面BCD 的法向量分别为n 1，n 2，若n 1＝(1,0,0)，n 2＝(－3，0,1)，则二面角A －BD －C 的大小可能为()A.π6B.π3C.2π3D.5π6答案AD 解析由已知可得|cos 〈n 1，n 2〉|＝|n 1·n 2||n 1||n 2|＝32，因此二面角A －BD －C 的大小为π6或5π6.8．(2023·深圳模拟)如图，在矩形AEFC 中，AE ＝23，EF ＝4，B 为EF 中点，现分别沿AB ，BC 将△ABE ，△BCF 翻折，使点E ，F 重合，记为点P ，翻折后得到三棱锥P －ABC ，则()A ．三棱锥P －ABC 的体积为423B ．直线PA 与直线BC 所成角的余弦值为36C ．直线PA 与平面PBC 所成角的正弦值为13D ．三棱锥P －ABC 外接球的半径为222答案BD 解析由题意可得BP ⊥AP ，BP ⊥CP ，又AP ∩CP ＝P ，AP ，CP ⊂平面PAC ，所以BP ⊥平面PAC ，在△PAC 中，PA ＝PC ＝23，AC 边上的高为(23)2－22＝22，所以V 三棱锥P －ABC ＝V 三棱锥B －P AC ＝13×12×4×22×2＝823，故A 错误；在△PAC 中，cos ∠APC ＝12＋12－162×23×23＝13，BC ＝12＋4＝4，|cos 〈PA →，BC →〉|＝|PA →·BC →||PA →||BC →|＝|PA →·(PC →－PB →)|23×4＝|PA →·PC →－PA →·PB →|83＝||PA →||PC →|cos ∠APC －0|83＝23×23×1383＝36，所以直线PA 与直线BC 所成角的余弦值为36，故B 正确；S △PBC ＝12PB ·PC ＝12×2×23＝23，设点A 到平面PBC 的距离为d ，由V 三棱锥B －P AC ＝V 三棱锥A －PBC ，得13×23d ＝823，解得d ＝463，所以直线PA 与平面PBC 所成角的正弦值为d PA ＝46323＝223，故C 错误；由B 知，cos ∠APC ＝13，则sin ∠APC ＝223，所以△PAC 的外接圆的半径r ＝12·AC sin ∠APC ＝322，设三棱锥P －ABC 外接球的半径为R ，又因为BP ⊥平面PAC ，则R 2＝r 2＝92＋1＝112，所以R ＝222，即三棱锥P －ABC 外接球的半径为222，故D 正确．三、填空题9．(2023·天津统考)在长方体ABCD －A 1B 1C 1D 1中，AB ＝2，AD ＝1，AA 1＝3，则异面直线A 1C 1与AD 1所成角的余弦值为________．答案210解析如图，以D 为坐标原点，DA ，DC ，DD 1所在直线分别为x ，y ，z 轴建立空间直角坐标系，则A (1,0,0)，D 1(0,0,3)，A 1(1,0,3)，C 1(0,2,3)，则AD 1—→＝(－1,0,3)，A 1C 1—→＝(－1,2,0)，|cos 〈AD 1—→，A 1C 1—→〉|＝|AD 1—→·A 1C 1—→||AD 1—→||A 1C 1—→|＝110×5＝210因此，异面直线A 1C 1与AD 1所成角的余弦值为210.10．在三棱柱ABC －A 1B 1C 1中，侧棱A 1A ⊥底面ABC ，AC ＝1，AA 1＝2，∠BAC ＝90°，若直线AB 1与直线A 1C 所成角的余弦值是45，则棱AB 的长度是________．答案1解析建立如图所示的空间直角坐标系，设AB ＝a (a >0)，则A (0,0,0)，B 1(a ,0,2)，A 1(0,0,2)，C (0,1,0)，所以AB 1—→＝(a ,0,2)，A 1C —→＝(0,1，－2)，所以|cos 〈AB 1—→，A 1C —→〉|＝|AB 1—→·A 1C —→||AB 1—→||A 1C —→|＝4a 2＋4×5＝45，解得a ＝1，所以棱AB 的长度是1.11．(2023·洛阳模拟)二面角α－l －β的棱上有两个点A ，B ，线段BD 与AC 分别在这个二面角的两个半平面内，并且垂直于棱l ，若AB ＝4，AC ＝6，BD ＝8，CD ＝217，则平面α与平面β的夹角为________．答案60°解析设二面角α－l －β的大小为θ，因为AC ⊥AB ，BD ⊥AB ，所以CA →·AB →＝0，BD →·AB →＝0，由题意得CD →＝CA →＋AB →＋BD →，所以|CD →|2＝|CA →＋AB →＋BD →|2＝|CA →|2＋|AB →|2＋|BD →|2＋2CA →·AB →＋2CA →·BD →＋2AB →·BD→＝|CA →|2＋|AB →|2＋|BD →|2＋2CA →·BD→＝36＋16＋64＋2×6×8×cos(180°－θ)＝(217)2，所以cos(180°－θ)＝－12，即cos θ＝12，所以θ＝60°，则平面α与平面β的夹角为60°.12.在正方体ABCD －A 1B 1C 1D 1中，E ，F ，G ，H ，K ，L 分别是棱AB ，BB 1，B 1C 1，C 1D 1，D 1D ，DA 的中点，则直线A 1C 与平面EFGHKL 所成角的大小为________；若P ，Q 是六边形EFGHKL 边上两个不同的动点，设直线D 1B 与直线PQ 所成的最小角为θ，则sin θ的值为________．答案90°13解析如图，以点D 为坐标原点，以DA →，DC →，DD 1—→的方向分别为x ，y ，z 轴的正方向建立空间直角坐标系，设正方体的棱长为2，则A 1(2,0,2)，E (2,1,0)，C (0,2,0)，F (2,2,1)，G (1,2,2)，∴A 1C —→＝(－2,2，－2)，EF →＝(0,1,1)，EG →＝(－1,1,2)，∴A 1C —→·EF →＝0＋2－2＝0，A 1C —→·EG →＝2＋2－4＝0，∴A 1C ⊥EF ，A 1C ⊥EG ，∵EG ∩EF ＝E ，EG ，EF ⊂平面EFGHKL ，∴A 1C ⊥平面EFGHKL ，∴直线A 1C 与平面EFGHKL 所成角的大小为90°.又D 1(0,0,2)，B (2,2,0)，D 1B —→＝(2,2，－2)，由题意知A 1C —→＝(－2,2，－2)为平面EFGHKL 的一个法向量，设直线D 1B 与平面EFGHKL 所成的角为α，则sin α＝|cos 〈D 1B —→，A 1C —→〉|＝|D 1B —→·A 1C —→||D 1B —→||A 1C —→|＝412×12＝13，∵直线PQ ⊂平面EFGHKL ，∴直线D 1B 与直线PQ 所成的角最小时即为直线D 1B 与平面EFGHKL 所成的角，∴sin θ＝13.四、解答题13.如图，AE ⊥平面ABCD ，CF ∥AE ，AD ∥BC ，AD ⊥AB ，AB ＝AD ＝1，AE ＝BC ＝2CF ＝2.(1)求证：BF ∥平面ADE ；(2)求直线CE 与平面BDE 所成角的正弦值．(1)证明由CF ∥AE ，CF ⊄平面ADE ，AE ⊂平面ADE ，得CF ∥平面ADE ，由AD ∥BC ，BC ⊄平面ADE ，AD ⊂平面ADE ，得BC ∥平面ADE ，又CF ∩BC ＝C ，CF ，BC ⊂平面BCF ，所以平面BCF ∥平面ADE ，又BF ⊂平面BCF ，所以BF ∥平面ADE .(2)解因为AE ⊥平面ABCD ，AB ，AD ⊂平面ABCD ，所以AE ⊥AB ，AE ⊥AD ，又AD ⊥AB ，以A 为原点，分别以AB ，AD ，AE 所在直线为x ，y ，z 轴建立空间直角坐标系如图所示，因为AB ＝AD ＝1，AE ＝BC ＝2CF ＝2，所以B (1,0,0)，C (1,2,0)，D (0,1,0)，E (0,0,2)，则CE →＝(－1，－2,2)，BE →＝(－1,0,2)，DE →＝(0，－1,2)，设平面BDE 的法向量为m ＝(x ，y ，z )，·BE →＝－x ＋2z ＝0，·DE →＝－y ＋2z ＝0，令z ＝1，则x ＝2，y ＝2，即m ＝(2,2,1)，所以|cos 〈m ，CE →〉|＝|m ·CE →||m ||CE →|＝43×3＝49，即直线CE 与平面BDE 所成角的正弦值为49.14．(2024·南昌模拟)如图，在梯形ABCD 中，AB ∥DC ，AD ＝DC ＝12AB ，现将△ADC 沿AC 翻至△APC ，使二面角P －AC －B 为直二面角．(1)证明：CB ⊥PA ；(2)若AB ＝4，二面角B －PA －C 的余弦值为217，求异面直线PC 与AB 所成角的余弦值．(1)证明取AB 的中点E ，连接CE (图略)，∵在梯形ABCD 中，AB ∥CD ，AD ＝DC ＝12AB ，AE ∥DC ，AE ＝DC ，∴四边形ADCE 是平行四边形，CE ＝AD ，CE ＝AE ＝EB ，∴∠ACB ＝90°，即CB ⊥CA ，∵二面角P －AC －B 为直二面角，∴平面PAC ⊥平面ACB ，又平面PAC ∩平面ACB ＝AC ，CB ⊂平面ABC ，∴CB ⊥平面PAC ，又PA ⊂平面PAC ，∴CB ⊥PA .(2)解由AB ＝4知PA ＝PC ＝2，取AC 的中点O ，则OE ∥CB .∴OE ⊥AC ，且OP ⊥AC ，OC ，OE ，OP 两两互相垂直．以O 为原点，OC →，OE →，OP →的方向为x ，y ，z 轴的正方向建立如图所示的空间直角坐标系．设OC ＝a (a >0)，则C (a ,0,0)，P (0,0，4－a 2)，A (－a ,0,0),B (a ,24－a 2，0)，AB →＝(2a ,24－a 2，0)，AP →＝(a ,0，4－a 2)，易得平面PAC 的一个法向量为n 1＝(0,1,0)，设平面PAB 的法向量为n 2＝(x ，y ，z )，2·AB →＝2ax ＋24－a 2y ＝0，2·AP →＝ax ＋4－a 2z ＝0，取x ＝4－a 2，得y ＝－a ，z ＝－a ，故n 2＝(4－a 2，－a ，－a )，由|cos 〈n 1，n 2〉|＝|n 1·n 2||n 1||n 2|＝a 4＋a 2＝217，得a ＝3，则PC →＝(3，0，－1)，AB →＝(23，2,0)，设异面直线PC 与AB 所成的角为θ，则cos θ＝|cos 〈PC →，AB →〉|＝|PC →·AB →||PC →||AB →|＝62×4＝34，所以异面直线PC 与AB 所成角的余弦值为34.。

第七章 文化地理学第一节 人种、民族、民俗一、人种（一）人种的划分人种，即人类的种族，是指具有共同起源并在体质形态上具有某些共同遗传特征（如肤色、眼色、发色、发型、身长、面型、鼻型、血型等）的人群。

人种概念属于生物学和体质人类学范畴，它是人类自然属性的一种表现。

1. 划分种族的标志以保有共同的遗传的自然特征为依据。

(1) 毛发：亚洲人——直发欧洲人——波状发非洲人——羊毛卷发(2) 肤色：肤色深浅与皮下色素细胞的多少有关。

(3)身高：虽然身高与营养条件有关，但也受到遗传因素的影响。

(4) 头颅形状：头型是人种特征的重要标志。

人类头型与头的上下和两侧脑的长成有关，因此在人种上，落后和进步种族之间头型指数具有一定差异，反映出脑量的差异。

头指数：眉间到后脑长度和两耳上方宽度之比。

目前黑人头指数约为65，地中海人为75，阿尔卑斯人为84，蒙古人为85。

在这些人种中，蒙古人的历史最为进步，白种人次之。

不过在近代人种大规模移动后，文化交流日益广泛和频繁，打破了古代的文化地区分化现象，出现了人类智慧和文化传播并非等同的现象。

本书(P.92)采用头骨指数（头盖骨的长宽比例）的指标，其公式为：头宽头骨指数= —— ×100%头长(5) 鼻形：根据鼻梁的宽、狭或高、中、低来划分种族。

以鼻翼的宽度与鼻长度相比，白种人——狭鼻，黄种人——中鼻，黑种人——宽鼻。

(6) 血型：不同种族血型存在差异 (书P.92表) 。

(7) 指纹：亚洲人——斗形纹最多黑种人——弓形纹最多欧洲人——箕形纹最多2. 世界种族的划分布尔民巴哈是西方人类学鼻祖，他把全球人类分为5种：高加索人、蒙古人、非洲人、美洲人、马来人。

目前，国际上比较统一的看法是分为4大种群12个种族。

（1）白色种族群：皮肤呈白色、浅棕色，波状金发或棕发，鼻高目蓝。

白色种族在世界上分布最广，包括欧亚大陆西部、从毛里塔尼亚到索马里的北非地区，西亚、南亚地区。

白色人种可分为：①北欧种族；②南欧种族；③印度种族（2）黄色种族群：皮肤黄色、毛发黑且直，眼褐色。