当前位置：文档之家 › 第五章圆轴的扭转

第五章圆轴的扭转

  • 格式：ppt
  • 大小：1.67 MB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

材料力学扭转第5节 圆轴扭转时的变形

材料力学扭转第5节 圆轴扭转时的变形


BA

T1l1 GI P1

180


0.8110
CB

T2l2 GI P 2

180


0.9810
CA CB BA 0.9810 (0.8110 ) 0.17 0
例4-4 如图，已知ABC轴结构尺寸为 lAB 1.6m， lBC 1.4m。材料切变模量 G 80GPa，轴上作用有外 力矩 M A 900 N·m，M B 1500 N·m，M C 600 N·m，试
求截面C的相对截面A的转角。
解： 1）用截面法求
各段扭矩
1
2
AB 段：
一、圆轴扭转时的扭转变形
• 扭转角：圆轴扭转时，两横
A

BO
截面相对转过的角度称为这
两截面的相对扭转角。
M
M
d

T (x) GIP
dx


l d

T (x)
l GIP
dx
若在圆轴的 l 长度内，T、G、
IP 均为常数，则圆轴两端截面的 相对扭转角为：
Tl
GIP
• 抗扭刚度：式中的 GIP 称为圆轴的抗扭刚度，它反 映了圆轴抵抗扭转变形的能力。
T1 MA 900 N m
BC 段：
T
600Nm
T2 M c 600 N m
画出扭矩图如图所示
900Nm
AB 截面 极惯性矩
I P1

d14
32
BC 截面 极惯性矩
2）C 截面相对于 A 截面的转角
IP2

d
4AB 段： BC 段：
材料力学 第五章扭转变形.强度、刚度条件(6,7,8)汇总

材料力学 第五章扭转变形.强度、刚度条件(6,7,8)汇总

Me Tb Ta
( 4)
例题 6-6
5. 实心铜杆横截面上任意点的切应力为 Ta Ga M e 0 ra ρa I pa Ga I pa Gb I pb 空心钢杆横截面上任意 点的切应力为
b
Tb Gb M e I pb Ga I pa Gb I pb
2
1 dV (dxdydz ) 2 dV dW v dV dxdydz 1 v 2





一、密圈螺旋弹簧
——螺旋角
F
O

d
d ——簧丝横截面的直径 D ——弹簧圈的平均直径
O D
密圈螺旋弹簧 ——螺旋角<5°时的圆柱形弹簧
§4.5
密圈螺旋弹簧的计算
O F
例题 6-6
Me Tb Ta
解： 1. 实心铜杆和空心钢杆横截面上的扭矩分别为Ta 和Tb(图b)，但只有一个独立平衡方程 Ta+Tb= Me (1) 故为一次超静定问题。
例题 6-6
Me Tb Ta
2. 位移相容条件为实心杆和空心杆的B截面相对 于A截面的扭转角相等。在图b中都用表示（设 A端固定）。 Ba Bb ( 2)
a
b
ra
ra
a rb
切应力沿半径的变化 情况如图c所示。
ra
rb
(c)
§5-8非圆截面等直杆扭转的概念
圆截面杆扭转时的应力和变形公式,均建立在平 面假设 的基础上。对于非圆截面杆,受扭时横截面不 再保持为平面，杆的横截面已由原来的平面变成了曲 面。这一现象称为截面翘曲。因此,圆轴扭转时的应 力、变形公式对非圆截面杆均不适用。
(2)
圆 轴扭转时的变形和刚度计算

圆 轴扭转时的变形和刚度计算


a＜[
]
60MP
a
可见强度满足要求。
目录
扭转\圆轴扭转时的变形和刚度计算
4）刚度校核。轴的单位长度最大扭转角为
＝
max
Tmax GIp
180＝
2．86103 N m
π 80109 P a 6.44106
m4
180 3．14
＝0．318 / m 1.1 / m
可见刚度也满足要求。
目录
扭转\圆轴扭转时的变形和刚度计算
【例3.6】 一钢制传动圆轴。材料的切变模量G=79×103MPa，
许用切应力[τ]= 88.2 MPa，单位长度许用扭转角 0.5 /m，承受
的扭矩为T = 39.6 kN·m。试根据强度条件和刚度条件设计圆轴的直 径D。
【解】 1）按强度条件设计圆轴的直径。由强度条件
＝Tmax W max
床的加工精度；机器的传动轴如有过大的扭转变形，将使机器在运
转时产生较大振动。因此，必须对轴的扭转变形加以限制，即使其
满足刚度条件：
＝Tmax max GIp
式中：[ ]——单位长度许用扭转角，单位为rad/m，其数值是由轴
上荷载的性质及轴的工作条件等因素决定的，可从有关设计手册中
查到。在工程实际中，[ ]的单位通常为 /m ，因而刚度条件变为
Gπ2[ ]
3 21 8 0 3 9.6 1 03
79109 2 0.5 m 0.156m 156mm
故取D＝160mm，显然轴能同时满足强度条件和刚度条件。
目录
力学
该轴的强度和刚度。
目录
扭转\圆轴扭转时的变形和刚度计算
【解】 1）计算外力偶矩。
M eA
9549
圆 轴 的 扭 转

圆 轴 的 扭 转

2.32kN.m
4.71kN.m
x
T
此时轴的扭矩图如下
可见轴内的最大扭矩值比原来减小了。
注释：若将A轮与B轮相互调换，则轴的左右两段内的扭矩分别是
C
A
B
MA
MB
1
MC
2
[例1]已知：一传动轴， n =300r/min，主动轮输入 P1=500kW，从动轮输出 P2=150kW，P3=150kW，P4=200kW，试绘制扭矩图。
C
B
A
MB
MA
1
MC
2
T1
1
MA
T2
2
MC
(b) 扭矩。在集中力偶MA与MB之间和MB与MC之间的圆轴内，扭矩是常量，分别 假设为正的扭矩T1和T2。
由截面法
由结果可知扭矩的符号都为正。
C
B
A
MB
MA
1
MC
2
(c) 扭矩图：扭矩数值最大值发生在AB段。
2.32kN.m
7.03kN.m
x
T
(+)
(b) 扭矩。用截面法求出AC段和CB段内的扭矩
(c) 变形谐调条件。圆轴的两端固定，所以A、B截面的相对转角等于零。
(d) 分别算出A、C截面和C、
A
B
MB
(e) 补充方程。把上二式代入到变形谐调条件中去就得到补充方程。
(f) 解方程组。联立补充方程和平衡方程解得
a
c
d
dx
b
dy
´
´
t
z
剪应变：
直角的改变量
式中：G是材料的一个弹性常数，称为剪切弹性模量，因 无量纲，故G的量纲与 相同，不同材料的G值可通过实验确定，钢材的G值约为80GPa。
材料力学-扭转1ppt课件

材料力学-扭转1ppt课件


横截面上 —
max
T IP
max
IP
T
max
T WP
Ip—截面的极惯性矩，单位：m4 , mm 4
WP
Ip
max
WP —抗扭截面模量，单位：m3, mm3.
整个圆轴上——等直杆：
max
Tm a x WP
三、公式的使用条件： 1、等直的圆轴， 2、弹性范围内工作。
30
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
d
dx
d / dx－扭转角变化率
二）物理关系：
弹性范围内 max P
G → G
G
d
dx
方向垂直于半径。
28
三）静力关系：
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dxp
29
二、圆轴中τmax的确定
结论：
横截面上 0, 0 0 0
根据对称性可知剪应力沿圆周均匀分布；
t D, 可认为剪应力沿壁厚均匀分布,
且方向垂直于其半径方向。
t
D
20
3、剪应力的计算公式：
T
AdA.r0
2 0
r0
2td
r02t2
d
T
2r0 2t
薄壁圆筒横截面上的剪应力计算式
21
二、关于剪应力的若干重要性质
例题： 1、一传动轴作200r／min的匀速转动，轴上装有五个轮子。 主动轮2输入的功率为60kW，从动轮1、3、4、5依次输出的 功率为18kW、12kW、22kW和8kW。试作出该轴的扭矩图。
[理学]化工设备机械基础习题解答

[理学]化工设备机械基础习题解答

目录化工设备机械基础课后习题解答 .............................. 错误！未定义书签。

EXERCISE EXPLANATION AND DESIGNING OF THE BASIC OF CHEMICAL EQUIPMENT AND MECHANISM .. 错误！未定义书签。

第一章刚体的受力分析及其平衡规律 .. (2)第一部分例题及其解析 (2)第二部分习题及其解答 (10)第二章金属的力学性能 (18)第一部分例题及其解析 (18)第二部分习题及其解答 (19)第三章受拉（压）构件的强度计算与受剪切构件的实用计算 (22)第一部分例题及其解析 (22)第二部分习题及其解答 (24)第四章直梁的弯曲 (27)第一部分例题及其解析 (27)第二部分习题及其解答 (35)第五章圆轴的扭转 (39)第一部分例题及其解析 (39)第二部分习题及其解答 (43)第六章压力容器与化工设备常用材料 (46)第一部分习题及其解析 (46)第七章压力容器中的薄膜应力、弯曲应力、与二次应力 (48)第一部分习题及其解析 (48)第八章内压容器 (52)第一部分例题及其解析 (52)O(c)CAB(a )第二部分 习题及其解答 (55)第九章 外压容器与压杆的稳定计算 (60)第一部分 例题及其解析 .................................................................................................................. 60 第二部分 习题及其解答 .. (67)第一章 刚体的受力分析及其平衡规律第一部分 例题及其解析1.下图(a)是一个三角支架，它由两根杆和三个销钉组成，销钉A 、C 将杆与墙 连接，销钉B 则将两杆连接在一起。

当AB 杆中央 置一重物时，试确定AB 杆两端的约束反力力线方 位（杆的自身质量不计）。

轴的扭转刚度计算

轴的扭转刚度计算


Hypermesh求解
长度单位全部为毫米（mm） 最大应变为1.936e-4mm 扭转角度=最大应变/(r/2)=3.872e-5rad=2.219deg 扭转刚度 Kt=T/扭转角度=4.507 Nm/deg
计算结果对比
公式计算 直径/mm 长度/mm 扭矩/N
剪切模量 Ip
扭转角度/rad 扭转角度/deg 刚度/N/deg
10
300
0.01 8.00E+10 9.82E-10
3.82E-05
2.19E-03 4.57E+00
hypermes量 2.10E+11
扭转角度/rad 扭转角度/deg 刚度/N/deg 0.00003872 0.00221849 4.5075758
轴的扭转刚度计算方法
张志军
扭转变形计算公式：
扭转角(φ)：圆轴扭转时两横截面相对转过的角度。
G—剪切弹性模量
几种材料特性举例：
公式求解：
已知：直径为10mm，长度为300mm，受到扭矩为 0.01Nm，求扭转刚度？
首先将长度单位化为米(m) Ip=π*d^4/32=9.82e-10 扭转角度=T*l/(G*Ip)=3.82e-5 rad=2.19e-3 deg 扭转刚度Kt=T/扭转角度=4.57 Nm/deg
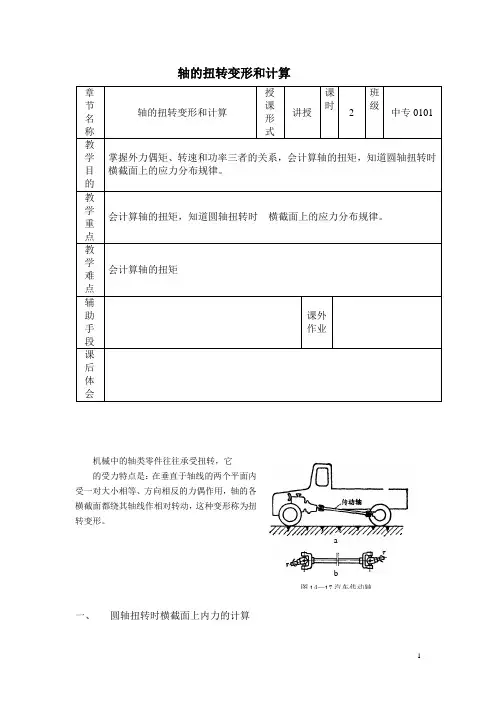
机械基础——轴的扭转变形和计算(教学教案)

机械基础——轴的扭转变形和计算(教学教案)

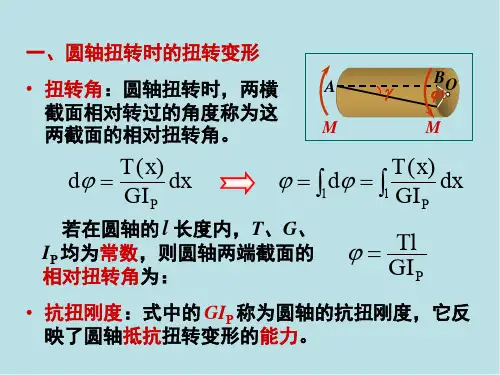
ab图14—17汽车传动轴轴的扭转变形和计算章节名称 轴的扭转变形和计算授课形式讲授课时2班级中专0101教学目的 掌握外力偶矩、转速和功率三者的关系，会计算轴的扭矩，知道圆轴扭转时 横截面上的应力分布规律。

教学重点 会计算轴的扭矩，知道圆轴扭转时 横截面上的应力分布规律。

教学难点 会计算轴的扭矩辅助手段课外作业课后体会机械中的轴类零件往往承受扭转，它 的受力特点是：在垂直于轴线的两个平面内受一对大小相等、方向相反的力偶作用，轴的各横截面都绕其轴线作相对转动，这种变形称为扭转变形。

一、圆轴扭转时横截面上内力的计算图14—18截面法求扭矩l 、外力偶矩：为了求出圆轴扭转时截面上的内力，必须先计算出轴上的外力偶矩，作用在轴上的外力偶矩往往不是直接给出的，而是根据给定的轴的传递功率和轴的转速算出来的，功率、转速和外力偶矩三者间的关系是：M ＝9550 P ／n式中：P ——轴传递的功率(千瓦， KW) n ——轴的转速(转／分， r ／ min) M ——作用在轴上的外力偶矩(牛顿米，Nm)2、扭转时横截面上的内力——扭矩圆轴在外力偶矩的作用下，横截面上产生内力。

求内力的方法仍用截面法。

右图表示装有四个皮带轮的传动轴，在四个带轮上分别作用有主动力偶矩 M 1和从动力偶矩M 2、M 3、M 4，外力偶矩分别为 M 1＝110Nm ，M 2=60Nm ，M 3=20Nm ， M 4=30Nm 。

若计算 AB 段内任一截面上的内力，可假想沿该段内的任一截面1—1将轴截开，取左边部分为研究对象。

如图所示。

为了保证该段的平衡，必须以内力偶矩 Mn 1代替另一部分对被研究部分的作用， Mn 1称为扭矩。

扭矩的正负有如下规定：使右手拇指与截面法线的方向一致，若截面上的扭矩的转向与其它四指的转向相同，则扭矩取正号：反之取负号。

应用截面法时，一般都先假设截面上的扭矩为正。

扭矩的大小用平衡方程Σm=0求得，即AB 段内： Σm=0， M 1十Mn 1＝0Mn 1＝一M 1＝一l10 Nm (设反)图14—19圆轴扭转变形图14—20圆轴的横截 面上剪应力的分布规律BC 段内： Σm ＝0 M 1—M 2＋Mn 2＝0 得 Mn 2＝—50 Nm (设反) CD 段内： Σm ＝0 M 1—M 2—M 3十Mn 3＝0 得 Mn 3＝—30 Nm (设反) 为了清楚地看出各截面上的扭矩变化情况，以便确定危险截面，通常把扭矩随截面位置的变化绘成图形，称为扭矩图。

材料力学扭转(共56张PPT)

材料力学扭转(共56张PPT)


例题： ：空心轴和实心轴材料相同，面积相同, α= 0.5。试比较空心轴和实心轴的强度和刚度情况。
解： 1〕确定两轴尺寸关系
面积相同 (1)校核空心轴及实心轴的强度〔不考虑键槽的影响〕；
扭转角单位：弧度〔rad〕 在B、C轮处分别负载N2=75kW，N3=75kW。
D1 d1
D d 2 2可G、I见P扭—在矩—载计抗荷算扭相1、2刚同符度的号。条规件定下和，扭空矩2心图轴绘的制重量仅为实2心轴的31% 。
1、扭转杆件的内力〔截面法〕
m
m
左段：
mx 0, T m 0
T m
右段：
m x
0,
mT 0
T m
m
Tx
T
m
x
内力偶矩——扭矩 T
2、扭矩的符号规定：按右手螺旋法那么判断。
+
T
T
-
3、内力图〔扭矩图〕
扭矩图作法：同轴力图：
例题： 1、一传动轴作200r／min的匀速转动，轴上装有五个轮子。主动轮 2输入的功率为60kW，从动轮1、3、4、5依次输出的功率为18kW、 12kW、22kW和8kW。试作出该轴的扭矩图。
二、 扭转杆的变形计算
1、扭转变形：〔相对扭转角〕
d T
dx GI P
扭转变形与内力计算式
d T dx
GIP
T dx
L GIP
1) 扭矩不变的等直轴
Tl GI p
扭转角单位：弧度〔rad〕 GIP——抗扭刚度。
2)各段扭矩为不同值的阶梯轴
Tili GI pi
3)变截面轴
T (x) dx l GI p (x)
2)、设计截面尺寸:
T
Ip
圆轴扭转

圆轴扭转


空心圆截面：
Wt

D3
16
(1
d4 D4
)

D3
16
(1 4 )
四 等直圆杆扭转时的应力
例题1 已知空心圆截面的扭矩T=1kN·m，D=40mm，d=20mm，求 最大、最小切应力。
解：
max
T
Wt
T


16
D3
(1

d4 D4
)
max min


16 1000

4.按大小比例和正负号，将各段杆的扭矩画在基线两 侧，并在图上标出数值和正负号
例题1 画出图示杆的扭矩图 3kN·m Ⅰ 5kN·m Ⅱ 2kN·m
解： AC段
m 0
AⅠ 3kN·m
CⅡ
T1 T2
3kN·m
B 2kN·m
T1 3 0 T1 3kN m
BC段 m 0
T2 2 0 T2 2kN m
ρ
τdA b dA
O2 T
四 等直圆杆扭转时的应力
4 极惯性矩
【公式3-16；公式3-18】
IP
2dA
A
D
2 2 2 d 0
O
D4
32
D
环形截面：
IP


32
(D4

d4)
d D
极惯性矩单位： m4
四 等直圆杆扭转时的应力
同一截面，扭矩T，极惯性矩IP为常数，因此各点 切应力τ的大小与该点到圆心的距离ρ成正比，方向垂 直于圆的半径，且与扭矩的转向一致
例题3 画出图示杆的扭矩图
4kN·mⅠ 6kN·mⅡ 8kN·mⅢ 6kN·m
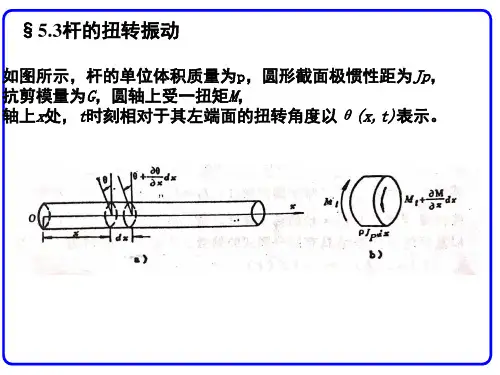
机械振动-轴的扭转振动

机械振动-轴的扭转振动


Ip
2 (x,t) ，
t 2
(1)
扭矩与单位转角之间有： (x,t) dx M dx
x
GJ p
(2)
代入(1)式，得轴的扭转振动运动方程为：
x
GJ
p
(x,t)
x
dx
IP
2 (x, t)
t 2
(3)
§5.3轴的扭转振动
x
GJ
p
(x,t)
x
dx
IP
2 (x, t)
t 2
(4)
对于圆轴来说转动惯量
剩下的Bn或An和φn 初始条件
带入一般解
扭转振动的方程的解为各阶主振动的叠加
(x, t)
(Ansin
n1
pn a
x
Bn
cos
pn a
x)(sinpnt n )
§5.3轴的扭转振动
解的形式
(x, t) (x) T(t)
(Asin p x B cos p x)(sinpt)
a
a
端点条件：
§5.3杆的扭转振动
如图所示，杆的单位体积质量为p，圆形截面极惯性距为Jp， 抗剪模量为G，圆轴上受一扭矩M， 轴上x处，t时刻相对于其左端面的扭转角度以θ(x,t)表示。
§5.3轴的扭转振动
从其上截取长度为dx的一小段来分析
转动惯量为Ip，圆形截面极惯性距为Jp,列出刚体转动方程：
M
M x
dx M
(5) 令： a2 G
P 则方程式转化为：
(6)
§5.3轴的扭转振动
杆的扭转振动和弦振动及杆的纵向振动 解的形式相同
(x, t) (x) T(t)
(Asin p x B cos p x)(sinpt)

轴扭转计算

第5章扭转5.1 扭转的概念及外力偶矩的计算5.1.1、扭转的概念在工程实际中，有很多以扭转变形为主的杆件。

例如图示 5.1，常用的螺丝刀拧螺钉。

图5.1图示5.2，用手电钻钻孔，螺丝刀杆和钻头都是受扭的杆件。

图5.2图示5.3，载重汽车的传动轴。

图5.3图示5.4，挖掘机的传动轴。

图5.4图5.5所示，雨蓬由雨蓬梁和雨蓬板组成（图5.5a），雨蓬梁每米的长度上承受由雨蓬板传来均布力矩，根据平衡条件，雨蓬梁嵌固的两端必然产生大小相等、方向相反的反力矩（图5.5b），雨蓬梁处于受扭状态。

图5.5分析以上受扭杆件的特点，作用于垂直杆轴平面内的力偶使杆引起的变形，称扭转变形。

变形后杆件各横截面之间绕杆轴线相对转动了一个角度，称为扭转角，用 表示，如图5.6所示。

以扭转变形为主要变形的直杆称为轴。

图5.6本章着重讨论圆截面杆的扭转应力和变形计算。

5.1.2、外力偶矩的计算工程中常用的传动轴（图）是通过转动传递动力的构件，其外力偶矩一般不是直接给出的，通常已知轴所传递的功率和轴的转速。

根据理论力学中的公式，可导出外力偶矩、功率和转速之间的关系为：nN m 9550= （5.1） 式中 m----作用在轴上的外力偶矩，单位为m N ⋅；N-----轴传递的功率，单位为kW ；n------轴的转速，单位为r/min 。

图5.75.2 圆轴扭转时横截面上的内力及扭矩图5.2.1 扭矩已知受扭圆轴外力偶矩，可以利用截面法求任意横截面的内力。

图 5.8a 为受扭圆轴，设外力偶矩为e M ，求距A 端为x 的任意截面n m -上的内力。

假设在n m -截面将圆轴截开，取左部分为研究对象（图5.8b ），由平衡条件0=∑x M ，得内力偶矩T 和外力偶矩e M 的关系内力偶矩T 称为扭矩。

扭矩的正负号规定为：自截面的外法线向截面看，逆时针转向为正，顺时针转向为负。

图5.8图示5.8的b 和c ，从同一截面截出的扭矩均为正号。

05第五章扭转习题解析

图示传动轴，主动轮A输入功率NA=50 马力，从动轮 B、C、D输出功率分别为 NB=NC=15马力 ，ND=20马
力，轴的转速为n=300转/分。作轴的扭矩图。
1
解：
NA 50 m A 7024 7024 1170 N m n 300
NB 15 mB mC 7024 7024 351 N m n 300 NC 20 mD 7024 7024 468 N m n 300
d 63.3mm
10
m
得 D 791 . mm
已知直径d=50mm的钢制圆轴在扭转角为 6°时，轴
内最大剪应力等于90MPa，G=80GPa。求该轴长度。
Tl GIp
T Wt
解：
(1)
max
( 2)
(1) 得： ( 2)
G Ip l max Wt
2.33 m

6
15
解：外管与内轴承受的扭矩相等，设为T
m
ml Tl Tl G I p内 G I p内 G I p外
16
例：两端固定的圆截面等直杆AB，在截面
C受外力偶矩m作用，试求杆两端的支座反力
偶矩。
17
解：
静力平衡方程为： m A mB m 变形协调条件为： AB AC CB 0
12
解：由
d l 2
2 2 300 40
2 得 l d
30
max G 2.7 2
m max Wt

180
0.09425 MPa
0.09425 106
0.04 3
16
118 . Nm

第五节 圆轴的扭转基础知识


l
GR
M 180 l G JP

M 180 l G JP
基本变形小结
比较拉压、弯曲、剪切、扭转基本变形的特点： 外力特点
变形特点
内力特点 应力特点 强度计算 刚度计算
第六节 压杆稳定
P
1.失稳的基本概念
T
2.压杆临界力
3.压杆的稳定计算
第五节 圆轴的扭转
5.1圆轴扭转时的外力和内力
扭转时的外力距： M PR
N P
2Rn / 60
2 N P 2Rn / 60 N Mn 60
60 N 3 N M 9.55 10 2 n n
第五节 圆轴的扭转
5.1圆轴扭转时截面上的内力 60 N 3 N M 9.55 10 2 n n 结论（1）判断减速器上高低转速轴
52圆轴扭转时截面上的应力52圆轴扭转时截面上的应力52圆轴扭转时截面上的剪应力分布规律53圆轴扭转时截面上的剪应力计算及最大剪应力称为抗扭截面模量称为截面的极惯性距54极性惯距与抗扭截面模量的计算321
化工设备 设计基础
第五节 圆轴的扭转
（1）受力特点：在垂直杆轴的截面上作用着大 小相等、方向相反的力偶距 （2）变形特点：各截面绕轴线产生相对转动， 即扭转变形
EJ Pcr 2 l
2
P
cr
P cr A
cr
例如图所示，直径为50mm的实心梁上受到一均布载荷 和一力偶的作用。 （1）求约束反力， （2）列出剪 力方程和弯距方程，（3）画出弯矩图，（4）求危险 横截面上最大正应力。
解：约束反力
R 1kN .m
M 2.75kN .m

圆轴扭转实验

圆轴扭转实验一、实验目的1．测定碳钢的切变屈服点（剪切屈服极限）τs或下屈服点τST、抗扭强度（剪切强度极限）τb。

2．测定铸铁的抗扭强度τb。

3．观察、比较和分析上述两种典型材料受扭转时的变形和破坏等现象。

二、实验设备1．扭转试验机；2．游标卡尺。

三、试样制备根据GB10128-88《金属室温扭转试验方法》中的规定，金属扭转试验所用试样为圆形截面，推荐采用直径为10mm，标距L0分别为50mm和100mm，平行长度L c分别为70mm和120mm的试样。

其头部形状和尺寸应按试验机夹头要求制备。

如采用其他直径的试样，其平行长度应为标距加上两倍直径。

扭转试样的形状和尺寸以及加工精度见图1-19。

图1-19 圆形截面扭转试样四、实验原理圆轴承受扭转时，材料处于纯剪应力状态。

因此常用扭转试验来研究不同材料在纯剪作用下的力学性质，这对于工程中的构件的合理设计和选材是十分重要的。

1．低碳钢试样的扭转试验全过程，由试验机自动绘图器绘出其扭矩T和扭转角ø的关系曲线，如图1-20所示。

由该图知，在弹性变形OA直线段，试样横截面上的扭矩与扭转角成正比关系，其上的剪应力亦呈线性分布，即截面最外缘的剪应力最大，中心的剪应力几乎为零，如图1-21（a）所示，在这个阶段材料服从切变虎克定律，并可测定切变模量G。

AB段为曲线部分。

它表明这阶段扭矩和扭转角不再成正比关系，横截面上剪应力的分布也不再是线性的，最外缘的剪应力首先达到剪切屈服极限，塑性区由外向里扩展，而形成环状塑性区和截面中部未屈服的弹性区，如图1-21（b）所示。

随着试样继续扭转变形，塑性区不断向圆心扩展，T-ø曲线稍微上升，直至B点趋于平坦，这时塑性区几乎占据了全部截面，剪应力趋于均匀分布如图1-21（c）所示。

扭矩度盘上的指针几乎不动，此时与之对应的扭矩为屈服扭矩T s如图1-20（a）；另一种情况，屈服阶段为锯齿状曲线。

度盘指针首次下降前的最大扭矩为上屈服扭矩T su，屈服阶段中最小扭矩为下屈服扭矩T SL，如图1-20（b）本次试验测定屈服扭矩或下屈服扭矩。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

结论：取圆轴直 径d=44mm。
32 M T max 180 0 4 32 477 .5 10 3 180 0 d4 43.2mm 2 3 2 3 G 80 10 1 10
33
作 业
P96 第27、28题
34
35
MT
MT R J MT W
书上有错 因
W 令 ：

J R
称为抗扭截面模量
R
MT J
21
三、极惯性矩和抗扭截面模量
1、实心圆轴
dA 2d
J dA 2
2 A d /2 0
d
3

d
J R
4
32
0.1d
4

(902 852 )
4
687 m m2
实心轴的横截面面积为
A实
D12
4

532
4
2210m m2
在两轴长度相等，材料相同情况下，两轴重量之比 等于横截面面积之比，即
687 0.31 W实 A实 2210 W空 A空
27
687 0.31 W实 A实 2210
距离圆心为ρ处的 E点切应变（横截 面上任一点E切应 变）：
HH ' HH ' g tang EH 17 dx
在微段中取出一个扇形体放大后的图
DD' DD' g tang AD dx
HH ' HH ' g tang EH dx
g HH ' ' g DD R
4
W

d
3
16
0.2d
3
22
2、空心圆轴
J
D 32


4
பைடு நூலகம்
d
4
0.1D 1
4 4
d D
3 4
W
D 16D
4
d4

D3
1 0.2 D 1 16
4
o d D
23
5.4 扭转的强度条件
为了保证圆轴安全工作，要求最大切应力不超过材 料的许用切应力。
32
(2)按强度条件设计轴的直径
M T max 16M T max max 3 W d
d 3 16 M T max

3 16 477 . 5 10 3 39 .3mm 40
3、按刚度条件设计轴的直径
M T max 1800 32M T max 1800 4 GJ Gd
变形特点：任意两个横截面之间都发生绕轴线的相对 转动（轴表面纵线歪成螺旋线）。
B端相对于A端面的转角φ，称为扭转角。
4
5.2 扭转时的外力和内力
一、扭转时的外力偶矩计算
在工程实际中，外力偶矩往往不是直接给出，给出 的是轴所传递的功率 N 和轴的转速 n ，因此需要根 据N、n来计算外力偶矩。
传递功率N
转速n
5
5.2 扭转时的外力和内力
输入功率N n 转速n R P v
齿轮、传动链条和皮带的圆周力对轮心的力矩就是使轴发生扭转变形的外力偶矩
①若已知圆周力P和半径R，则外力偶矩
②若已知功率N(kW)和转速n(r/min)，则
m PR
N 10 P v
3
P 2R n / 60 m2n / 60
MT
28
5.5 圆轴的扭转变形与刚度条件
一、圆轴的扭转变形 用两端面相对扭转角表示
j R g l
G g
j
l
GR
MT R 又 J
MT l j G J
29
工程上常用单位长度扭转角表示扭转变形大小。
MT l G J
Pa(N/m2)
m
MT
正
右手螺 旋法则
m
MT
负
8
求扭矩的快捷方法
mB 1 mC mA 2 3 mD
B
1
C
2 A
3
D
MT 1 mB
M T 2 mB mC MT 3 mB mC mA
扭矩的大小等于截面任何一侧所有外力偶矩的代 数和。外力偶矩正负号规定同扭矩。 9
书上的一个问题
m1 mC m2 mC mA
j
N· m 单位：rad/m m4
工程上中规定的单位长度许用扭转角[θ]常以°/m为 单位，故上式可改写成
M T 180 G J
0
/m
GJρ—抗扭刚度
30
二、扭转的刚度条件
M 180 G J
要求精密度高、运转稳定的轴： [θ]=0.250～0.500/m
二、横截面上切应力的计算公式
静力关系 各微面积上微内力对中心之矩的总和应等于截面扭矩
M T dA
A


dA
R
MT
o
2


R
A
dA
MT
20
MT

R
A
dA
2
2



dA
令： J dA
A

o
称为截面的极惯性矩，与截 面尺寸有关的几何量。
MT MT 1527 .8 16103 max 52.2MPa 3 W D 85 3 4 (1 ) 90 1 <[τ ] 16 90 25 故该传动轴强度足够。
【例5-3】若上例中的传动轴采用实心轴，其它条件 不变，现要求它与原来的空心轴强度相同（即最大切 应力相同），试确定其直径，并比较空心轴与实心轴 的重量。 解：（1）确定实心轴的直径D1 因要求与上例空心轴强度相同，故实心轴的最大切 应力也应为52.2MPa。即
横截面上各点无轴向变形，故横截面上没有正应力。
横截面绕轴线发生了旋转式的相对错动，矩形变为
平行四边形，故横截面上有切应力存在。 各横截面半径不变，所以切应力方向与半径垂直。
16
变形几何关系 根据几何关系， 圆周表面任一点 A 的切应变：
在受扭圆轴中取一个微段dx来分析。注意dφ、ABCD
DD' DD' g tang AD dx
N m 9550 , N.m n 6
二、扭转时横截面上的内力
求出所有外力偶矩后，即可用截面法求横截面上 的内力。 m m
x
m
MT
m 0 MT m 0
MT m
取右段，MT方向相反7
作用在横截面上的内 力偶 MT 称为扭矩。
扭矩的正负号规定 为使取左侧和右侧得到的同一截面的扭矩，不仅数值 相等，且符号相同，对扭矩的正负号规定如下。
NA m A 9550 3.82 kN m n
mB 0.96kN m mC 1.27kN m
mD 1.59kN m
M T 1 0.96kN m
Mt1 Mt2 Mt3
M T 2 3.82 0.96 2.86kN m
M T 3 1.59kN m
扭矩一定要按 正向假设
10
外力偶矩的正负号同扭矩，右手，离开截面为正。
m
MT
正
m MT
右手螺 旋法则
负
11
【 例 5 - 1 】 主 动 轮 N A =12 0 kW ， 从 动 轮 N B = 3 0 kW ， NC=40kW，ND=50kW，转速n=300r/min，求截面1-1、 1-2、1-3的扭矩。 解：
要求一般的轴：
[θ] =0.500～1.00/m
要求精密度低的轴：[θ] =1.00～3.00/m
31
【例5-4】传动轴主动轮C输入外力偶矩mC=955N.m， 从动轮A、B、D分别输出 mA=159.2N.m， mB=318.3N m， mD=477.5N.m，已知材料切变弹性模量G=80×103 MPa，许用切应力[τ]=40MPa，单位长度许用扭转角[θ] =1º /m。设计轴的直径。 解：（1）计算扭矩，画扭矩图； AB段：MT1= - 159.2N.m， BC段：MT2=-477.5N.m， CD段：MT3= 477.5N.m。 MTmax= 477.5N.m
14
5.3 扭转时横截面上的应力
一、应力分布规律
①变形后圆周线的形状、大小都没有改变，两相邻圆 周线之间的距离也没有改变。 ②纵向线仍为直线，都倾斜了同一个角度γ，原来矩形 变成了平行四边形。
15
平面假设 圆轴扭转变形后各个横截面仍为 平面，而且其大小、形状以及相 邻两截面之间的距离保持不变， 横截面半径不变。 推断结论
W空
A空
可见在相同的外力偶矩情况下，强度相等的空心轴 的重量仅为实心轴的31%，即选用空心轴要比实心 轴更省材料。
解释 从截面应力分布可见，实心轴圆 周上τmax≈[τ]时，中间部分切应 力与[τ]相差甚远，中间材料大 部分没有充分利用。若把中间部 分材料向边缘移，成为空心截面， 就会增大Wρ，提高强度。
第5章 圆轴的扭转
5.1 圆轴扭转的实例与概念 5.2 扭转时的外力和内力 5.3 扭转时横截面上的应力
5.4 扭转的强度条件
5.5 圆轴的扭转变形与刚度条件
1
5.1 扭转变形的实例与概念
2
传动轴
3
Mn A'
A
g
Mn
B j
x
B'
扭转角φ
切应变γ
受力特点：圆截面杆受到一对大小相等、方向相反的 外力偶作用，力偶作用面垂直圆杆轴线。