第六章 圆轴的扭转
- 格式:ppt
- 大小:4.92 MB
- 文档页数:45


第六章圆轴扭转练习带答案第六章圆轴的扭转⼀、填空题1、圆轴扭转时的受⼒特点是:⼀对外⼒偶的作⽤⾯均_______于轴的轴线,其转向______。
2、圆轴扭转变形的特点是:轴的横截⾯积绕其轴线发⽣________。
3、在受扭转圆轴的横截⾯上,其扭矩的⼤⼩等于该截⾯⼀侧(左侧或右侧)轴段上所有外⼒偶矩的_______。
4、圆轴扭转时,横截⾯上任意点的切应⼒与该点到圆⼼的距离成___________。
5、试观察圆轴的扭转变形,位于同⼀截⾯上不同点的变形⼤⼩与到圆轴轴线的距离有关,显然截⾯边缘上各点的变形为最_______,⽽圆⼼的变形为__________。
6、圆轴扭转时,在横截⾯上距圆⼼等距离的各点其切应⼒必然_________。
7、从观察受扭转圆轴横截⾯的⼤⼩、形状及相互之间的轴向间距不改变这⼀现象,可以看出轴的横截⾯上⽆____________⼒。
8、圆轴扭转时,横截⾯上切应⼒的⼤⼩沿半径呈______规律分布。
10、圆轴扭转时,横截⾯上内⼒系合成的结果是⼒偶,⼒偶作⽤于⾯垂直于轴线,相应的横截⾯上各点的切应⼒应垂直于_________。
11、受扭圆轴横截⾯内同⼀圆周上各点的切应⼒⼤⼩是_______的。
12、产⽣扭转变形的⼀实⼼轴和空⼼轴的材料相同,当⼆者的扭转强度⼀样时,它们的_________截⾯系数应相等。
13、横截⾯⾯积相等的实⼼轴和空⼼轴相⽐,虽材料相同,但_________轴的抗扭承载能⼒要强些。
16、直径和长度均相等的两根轴,其横截⾯扭矩也相等,⽽材料不同,因此它们的最⼤剪应⼒是________同的,扭转⾓是_______同的。
17、产⽣扭转变形的实⼼圆轴,若使直径增⼤⼀倍,⽽其他条件不改变,则扭转⾓将变为原来的_________。
18、两材料、重量及长度均相同的实⼼轴和空⼼轴,从利于提⾼抗扭刚度的⾓度考虑,以采⽤_________轴更为合理些。
⼆、判断题1、只要在杆件的两端作⽤两个⼤⼩相等、⽅向相反的外⼒偶,杆件就会发⽣扭转变形。

《机械基础》教案(2009~ 2010学年第二学期)学院山西省工贸学校系(部)机电系教研室教师梁少宁山西省工贸学校③学生学案课题名称:圆轴扭转的识别和应用班级:姓名:(一)、工作任务:拿出一根塑料管在扭转的过程中,手上的力是怎样用的?然后拿出一根粉笔,它在扭转力的作用下断裂后,这个断裂面是什么样子的?(二)、学习目标:1、理解材料力学的任务和研究对象。
2、理解构件圆轴扭转时的受力特点、变形特点及应用实例。
3、能够在以后的工作当中根据构件的受力方式正确选择构件的形状和尺寸。
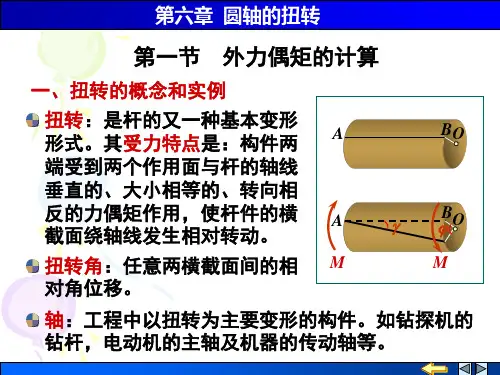
(三)、回答问题1、拿出一根塑料管在扭转的过程中,手上的力是怎样用的?2、然后拿出一根粉笔,它在扭转力的作用下断裂后,这个断裂面是什么样子的?(四)、分析该资料,完成项目任务:一、关于扭矩、剪应力与剪应变以及相对扭转角等概念扭转——直杆的两端,在垂直杆轴线的平面内作用一对大小相等,方向相反的外力偶,使杆件各横截面发生绕轴线相对转动。
这种变形形式称为扭转。
轴——以扭转变形为主要变形的杆件称为轴。
横截面为圆形的轴称为圆轴。
扭矩——在外力偶作用下,应用截面法,圆轴横截面上的分布内力组成一合力偶与外力偶平衡,这一内力合力偶的力偶矩称为扭矩,用T表示。
剪应力互等定理——由受扭圆轴上扭截取的微六面体(微元),在两个互相垂直的截面上的剪应力数值相等,其方向同时指向或背离该交线。
此关系称为剪应力互等定理。
纯剪状态——微元的四个侧面上只有剪应力而无正应力,则该微元的受力状态称为纯剪状态。
剪应变——剪应力作用下,微元的直角改变量称为剪应变(或切应变)。
剪切胡克定律——在弹性范围内,剪应力与剪应变成正比,即τ=Gγ,式中G是剪切弹性模量,与拉、压杆的弹性模量E相似,表示材料的弹性常数,随材料而异,由实验测定。
单位为MPa。
扭转角——轴在受扭时,两横截面间绕轴线相对转动的角度,称为相对扭转角,用φ表示,用来表示轴的扭转变形。
二、扭矩计算、扭转剪应力与变形分析1、外力偶矩的计算作用在轴上的外力是外力偶,其力偶矩用m表示。





第五节圆轴的扭转变形与刚度条件一、圆周的扭转变形圆轴受扭转时,除了考虑强度条件外,有时还要满足刚度条件。
例如机床的主轴,若扭转变形太大,就会引起剧烈的振动,影响加工工件的质量。
因此还需对轴的扭转变形有所限制。
轴受扭转作用时所产生的变形,是用两横截面之间的相对扭转角ϕ表示的,如下图所示。
由于γ角与ϕ角对应同一段弧长,故有ϕ·R = γ·l (a)式中的R是轴的半径,由剪切虎克定律,τ=G·γ,所以可得ϕ=τ·l/ (G·γ)(b)式中τ=M·R/ Jρ,代入(b)得:ϕ=M·l/ (G·Jρ)(1-46)公式(1-46)是截面A、B之间的相对扭转角计算公式,ϕ的单位是rad。
两截面间的相对扭转角与两截面间的距离l成正比,为了便于比较,工程上一般都用单位轴长上的扭转角θ表示扭转变形的大小:θ=ϕ/ l=M/ (G·Jρ)(1-47)θ的单位是rad/m。
如果扭矩的单位是N·m,G的单位MP a,Jρ的单位m4。
但是工程实际中规定的许用单位扭转角[θ]是以°/m 为单位的,则公式(1-47)可改写为:(1-48)式中G·Jρ称为轴的抗扭刚度,取决于轴的材料与截面的形状与尺寸。
轴的G·Jρ值越大,则扭转角θ越小,表明抗扭转变形的能力越强。
二、扭转的刚度条件圆轴受扭转时如果变形过大,就会影响轴的正常工作。
轴的扭转变形用许用扭转角[θ]来加以限制,其单位为°/m,其数值的大小根据载荷性质、工作条件等确定。
在一般传动和搅拌轴的计算中,可选取[θ]=0.5°/m~10°/m。
由此得出轴的扭转刚度条件:θ=M/ (G·Jρ)·(180/ π)≤[θ](1-49)圆轴设计时,一般要求既满足强度条件(1-45),又要满足刚度条件(1-49)。

