有限自动机三章答案

3—1 何谓速度瞬心?相对瞬心与绝对瞬心有何异同点?答：参考教材30~31页。

3—2 何谓三心定理?何种情况下的瞬心需用三心定理来确定?答：参考教材31页。

3-3试求图示各机构在图示位置时全部瞬心的位置(用符号P ，，直接标注在图上) (a)(b)答：答：（10分）(d)（10分）3-4标出图示的齿轮一连杆组合机构中所有瞬心，并用瞬心法求齿轮1ω1/ω3。

答：1)瞬新的数目：K=N(N-1)/2=6(6-1)/2=152)为求ω1/ω3需求3个瞬心P 16、P 36、P 13的位置3）ω1/ω3= P 36P 13/P 16P 13=DK/AK由构件1、3在K 点的速度方向相同，可知ω3与ω1同向。

3-6在图示的四杆机构中，L AB =60mm ，L CD =90mm,L AD =L BC =120mm, ω2=10rad/s,试用瞬心法求：1)当φ=165°时，点的速度vc ；2)当φ=165°时，构件3的BC 线上速度最小的一点E 的位置及速度的大小；3)当V C =0时，φ角之值(有两个解)。

解：1）以选定的比例尺μ机械运动简图（图b ）2）求vc 定出瞬心p12的位置（图b ）因p 13为构件3的绝对瞬心，则有ω3=v B /lBp 13=ω2l AB /μ=10××78=(rad/s)v c =μc p 13ω3=×52×=(m/s)3)定出构件3的BC 线上速度最小的点E 的位置,因BC 线上速度最小的点必与p13点的距离最近，故丛p13引BC线的垂线交于点E，由图可得v E=μω3=××=(m/s)4)定出vc=0时机构的两个位置（图c）量出φ1=°φ2=°3-8机构中，设已知构件的尺寸及点B的速度v B(即速度矢量pb)，试作出各机构在图示位置时的速度多边形。

答：（10分）（b）答：答：3—11 速度多边形和加速度多边彤有哪些特性?试标出图中的方向。

“编译技术”第三章作业3-1构造下列正规式相应的DFA：（1）1(0|1)*101（2）a((a|b)*|ab*a)*b解：由转换系统构造确定有穷自动机对状态重命名：DFA的状态转换图：（2）构造该正规式的装换系统：由转换系统构造确定有穷自动机对状态重命名：DFA的状态转换图：3-2 对下面的FA，将它确定化并最小化。

a解：由转换系统构造确定有穷自动机对状态重命名：DFA的状态转换图：最小化：初始划分={T0,T1,T2}{T0,T1,T2}a={T, Φ, Φ}，所以划分为（{ T},{Φ, Φ}）即{T}3-3 给出下述文法所对应的正规式：S →0A|1BA→1S|1B→0S|0解：S→0A→01S→0A→01S→010A→0101S→0101OA→0101O1S…S→1B→10S→1B→10S→101B→1010S→10101B→101010S…所以可得正规式=（01|10）（01|10）*3-4 构造下述文法G[S]的自动机：S→A0S→A0|S1|0该自动机是确定的吗？若不确定，则对它确定化。

该自动机可识别的语言是什么？解：文法转换为自动机：因为是左线性文法，要增加一个开始状态X，并将开始符号S看成终态。

因为A经0可达到不同的状态，所以，该自动机为NFA。

确定化：对状态重命名：该自动机表达的语言用正规式表示为：00（0|10）*3-5试用有限自动机理论证明下列正规表达式是等价的。

（1）(a|ba)*b（2）(a*ba)*a*b解：（1）（2）因为最小化后，两者的状态图是一样的，都为：所以正规式(a|ba)*b和正规式(a*ba)*a*b是等价的。

机械设计基础第3章习题及答案第一篇：机械设计基础第3章习题及答案第3章习题解答3-1 题3-1图所示为一偏置直动从动件盘形凸轮机构。

已知AB段为凸轮的推程廓线，试在图上标注推程运动角δt。

3-2 题3-2图所示为一偏置直动从动件盘形凸轮机构。

已知凸轮是一个以C为中心的圆盘，问轮廓上D点与尖顶接触时其压力角为多少？试作图加以表示。

3-3 题3-3图所示为一对心尖顶直动从动件单圆弧凸轮（偏心轮）机构，凸轮的几何中心O9与凸轮转轴O的距离为LOO'＝15mm，偏心轮半径R＝30mm，凸轮以等角速度ω1顺时针转动，试作出从动件的位移线图s2-δ1。

第二篇：机械设计基础习题答案.机械设计基础(第七版)陈云飞卢玉明主编课后答案 chapter1 1-1 什么是运动副？高副与低副有何区别？答：运动副：使两构件直接接触，并能产生一定相对运动的连接。

平面低副－凡是以面接触的运动副，分为转动副和移动副；平面高副－以点或线相接触的运动副。

1-2 什么是机构运动简图？它有什么作用？答：用简单的线条和符号代表构件和运动副，并按比例定出各运动副位置，表示机构的组成和传动情况。

这样绘制出的简明图形就称为机构运动简图。

作用：机构运动简图不仅能表示出机构的传动原理，而且还可以用图解法求出机构上各有关点在所处位置的运动特性（位移，速度和加速度）。

它是一种在分析机构和设计机构时表示机构运动的简便而又科学的方法。

1-3平面机构具有确定运动的条件是什么？答：机构自由度F>0，且与原动件数相等，则机构各构件间的相对运动是确定的；这就是机构具有确定运动的条件。

（复习自由度 4 个结论 P17）chapter2 2-1 什么是曲柄摇杆机构的急回特性和死点位置？答：急回特性：曲柄等速回转的情况下，摇杆往复运动速度快慢不同，摇杆反行程时的平均摆动速度必然大于正行程时的平均摆动速度，此即急回特性。

死点位置：摇杆是主动件，曲柄是从动件，曲柄与连杆共线时，摇杆通过连杆加于曲柄的驱动力 F 正好通过曲柄的转动中心，所以不能产生使曲柄转动的力矩，机构的这种位置称为死点位置。

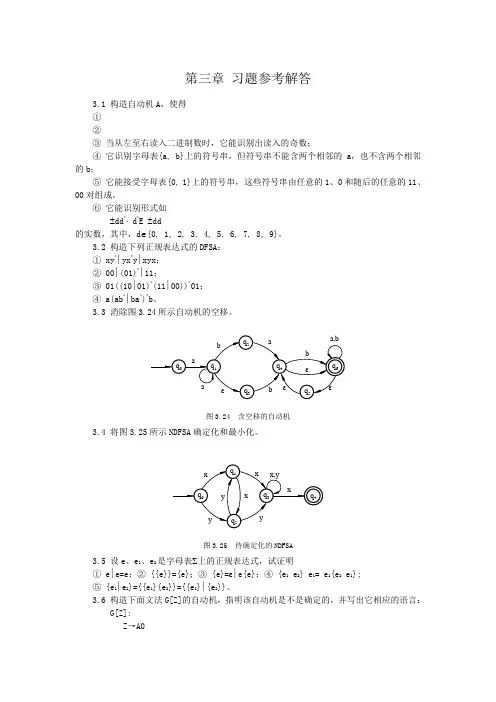
第三章习题参考解答3.1 构造自动机A，使得①②③当从左至右读入二进制数时，它能识别出读入的奇数；④它识别字母表{a, b}上的符号串，但符号串不能含两个相邻的a，也不含两个相邻的b；⑤它能接受字母表{0, 1}上的符号串，这些符号串由任意的1、0和随后的任意的11、00对组成。

⑥它能识别形式如±dd*⋅ d*E ±dd的实数，其中，d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。

3.2 构造下列正规表达式的DFSA：① xy*∣yx*y∣xyx；② 00∣(01)*∣11；③ 01((10∣01)*(11∣00))*01；④ a(ab*∣ba*)*b。

3.3 消除图3.24所示自动机的空移。

图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。

图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式，试证明① e∣e=e；② {{e}}={e}；③ {e}=ε∣e{e}；④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。

3.6 构造下面文法G[Z]的自动机，指明该自动机是不是确定的，并写出它相应的语言： G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中，f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。

试对此NDFSA 确定化。

3.8 设文法G[〈单词〉]：〈单词〉→〈标识符〉∣〈无符号整数〉 〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉 〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉 〈字母〉→a ∣b 〈数字〉→1∣2试写出相应的有限自动机和状态图。

3.9 图3.29所示的是一个NDFSA A ，试构造一个正规文法G ，使得L(G)= L(A)。

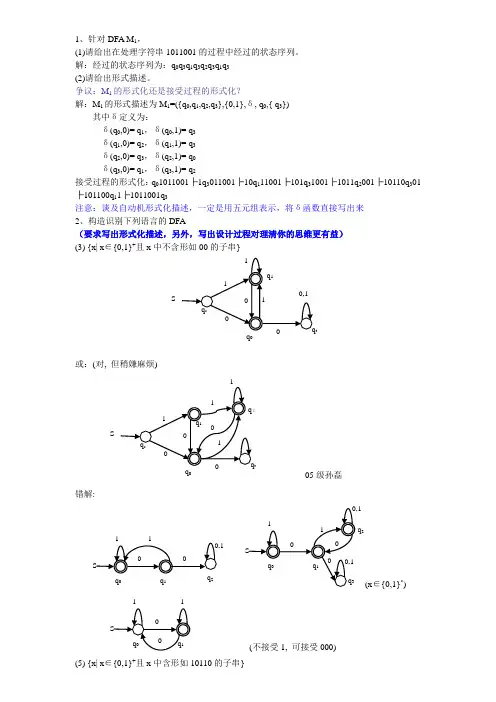
1、针对DFA M 1，(1)请给出在处理字符串1011001的过程中经过的状态序列。

解：经过的状态序列为：q 0q 3q 1q 3q 2q 3q 1q 3 (2)请给出形式描述。

争议：M 1的形式化还是接受过程的形式化？解：M 1的形式描述为M 1=({q 0,q 1,q 2,q 3},{0,1},δ, q 0,{ q 3})其中δ定义为：δ(q 0,0)= q 1，δ(q 0,1)= q 3 δ(q 1,0)= q 2，δ(q 1,1)= q 3 δ(q 2,0)= q 3，δ(q 2,1)= q 0 δ(q 3,0)= q 1，δ(q 3,1)= q 2 接受过程的形式化：q 01011001├1q 3011001├10q 111001├101q 31001├1011q 2001├10110q 301├101100q 11├1011001q 3注意：谈及自动机形式化描述，一定是用五元组表示，将δ函数直接写出来 2、构造识别下列语言的DFA（要求写出形式化描述，另外，写出设计过程对理清你的思维更有益） (3) {x| x ∈{0,1}+且x 中不含形如00的子串}或：(对, 但稍嫌麻烦)------------05级孙磊错解:∈{0,1}*)(不接受1, 可接受000)(5) {x| x ∈{0,1}+且x 中含形如10110的子串}q0：起始状态，以及未读入1的状态；q1：读入了10110中第1个符号(1)的状态；q2：读入了10110中第2个符号(0)的状态；q3：读入了10110中第3个符号(1)的状态；q4：读入了10110中第4个符号(1)的状态；q5：读入了10110中第5个符号(0)的状态；易犯的错误: 状态转移时, 不考虑已接受一些字符后所处状态, 一味地转到开始状态，不利用阶段性成果，狗熊掰棒子！(7) {x| x∈{0,1}+且把x看成二进制数时，x模5与3同余，要求中当x为0时，|x|=1，且x ≠0时，x首字符是1}提示: 和P98例3-5属同一类型, 这种设计如不写清楚设计过程, 不能服人, 也不能反映你的设计方法.解：按题意，当x为0时，x的长度为1，即不能出现多于1个0的全0串；当x不为0时，必须以1开始。

第三章******************************************************* ************************1．构造下列语言的DFA ( 陶文婧 02282085 ) （1）{0，1}*，1（2）{0，1}+，1（3）{x|x∈{0，1}+且x中不含00的串}（设置一个陷阱状态，一旦发现有00的子串，就进入陷阱状态）（4）{ x|x∈{0，1}*且x中不含00的串}（可接受空字符串，所以初始状态也是接受状态）（5）{x|x∈{0，1}+且x中含形如10110的子串}（6）{x|x∈{0，1}+且x中不含形如10110的子串}（设置一个陷阱状态，一旦发现有00的子串，就进入陷阱状态）（7）{x|x∈{0，1}+且当把x看成二进制时，x模5和3同余，要求当x为0时，|x|=1,且x≠0时，x的首字符为1 }1.以0开头的串不被接受，故设置陷阱状态，当DFA在启动状态读入的符号为0，则进入陷阱状态2.设置7个状态：开始状态q s,q0:除以5余0的等价类，q1：除以5余1的等价类,q2:除以5余2的等价类，q3:除以5余3的等价类，q4:除以5余4的等价类，接受状态q t（8）{x|x∈{0，1}+且x的第十个字符为1}（设置一个陷阱状态，一旦发现x的第十个字符为0，进入陷阱状态）（9）{x|x∈{0，1}+且x以0开头以1结尾}（设置陷阱状态，当第一个字符为1时，进入陷阱状态）（10）{x|x∈{0，1}+且x中至少含有两个1}（11）{x|x∈{0，1}+且如果x以1结尾，则它的长度为偶数；如果x以0结尾，则它的长度为奇数}可将{0，1}+的字符串分为4个等价类。

q0：[ε]的等价类，对应的状态为终止状态q1:x的长度为奇且以0结尾的等价类q2：x的长度为奇且以1结尾的等价类q3: x的长度为偶且以0结尾的等价类q4: x的长度为偶且以1结尾的等价类（12）{x|x是十进制非负数}5，6，7，8，94，9（13）Φ（14）ε******************************************************************************* 2.(1){{0,1}00}x x x+∈且中不含形如的子串(2){{0,1}10110}x x x+∈且中含形如的子串(3){{0,1}}x x x+∈且中不含形如10110的子串(4){{0,1}10101}x x x+∈和的倒数第个字符是，且以结尾，1(5){{0,1}01}x x x +∈且以开头以结尾(6){{0,1}}x x x +∈且中至少含有两个10，10，1*(7){{0,1}}x x x∈且如果以1结尾，则它的长度为偶数； 如果以0结尾，则它的长度为奇数(8){{0,1}}x x x +∈且的首字符和尾字符相等(9){,{0,1}}T x x x ωω+∈******************************************************************************* 3.根据下列给定文法，构造相应的FA 。

第3章词法分析习题答案1．判断下面的陈述是否正确。

（1）有穷自动机接受的语言是正规语言。

(√)（2）若r1和r2是Σ上的正规式，则r1|r2也是Σ上的正规式。

(√)（3）设M是一个NFA，并且L(M)={x,y,z}，则M的状态数至少为4个。

(× )（4）设Σ={a,b}，则Σ上所有以b为首的符号串构成的正规集的正规式为b*(a|b)*。

(× )（5）对任何一个NFA M，都存在一个DFA M'，使得L(M')=L(M)。

(√)（6）对一个右线性文法G，必存在一个左线性文法G'，使得L(G)=L(G')，反之亦然。

(√) （7）一个DFA，可以通过多条路识别一个符号串。

(× )（8）一个NFA，可以通过多条路识别一个符号串。

(√)（9）如果一个有穷自动机可以接受空符号串，则它的状态图一定含有 边。

(× )（10）DFA具有翻译单词的能力。

(× )2.指与出正规式匹配的串.（1)(ab|b)*c 与后面的那些串匹配？ababbc abab c babc aaabc（2）ab*c*(a|b)c 与后面的那些串匹配？ acac acbbc abbcac abc acc（3）(a|b)a*(ba)* 与后面的那些串匹配? ba bba aa baa ababa答案（1) ababbc c babc（2) acac abbcac abc（3) ba bba aa baa ababa3. 为下边所描述的串写正规式，字母表是{0, 1}.（1)以01 结尾的所有串（2)只包含一个0的所有串（3) 包含偶数个1但不含0的所有串（4)包含偶数个1且含任意数目0的所有串（5)包含01子串的所有串（6)不包含01子串的所有串答案注意 正规式不唯一（1)(0|1)*01（2)1*01*（3)(11)*（4)(0*10*10*)*（5)(0|1)*01(0|1)*（6)1*0*4.请描述下面正规式定义的串. 字母表{x, y}.（1) x(x|y)*x（2)x*(yx)*x*（3) (x|y)*(xx|yy) (x|y)*答案（1)必须以 x 开头和x结尾的串（2)每个 y 至少有一个 x 跟在后边的串 （3)所有含两个相继的x或两个相继的y的串5．处于/* 和 */之间的串构成注解，注解中间没有*/。

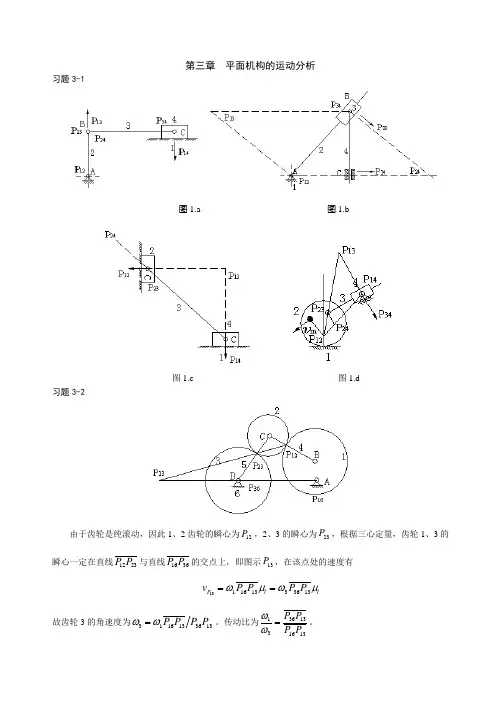
第三章 平面机构的运动分析习题3-1图1.a 图1.b图1.c 图1.d习题3-2由于齿轮是纯滚动，因此1、2齿轮的瞬心为12P ，2、3的瞬心为23P ，根据三心定量，齿轮1、3的瞬心一定在直线2312P P 与直线3616P P 的交点上，即图示13P，在该点处的速度有 l l P P P P P v μωμω133631316113==故齿轮3的角速度为1336131613P P P ωω=。

传动比为1316133631P P P P =ωω。

习题3-3答：1)三个瞬心中，14P 、12P 为绝对瞬心，24P 为相对瞬心。

2)不利用其它的三个瞬心，因为它们全是相对瞬心。

3)构件2和4之间的转向关系可以根据瞬心24P 的瞬时绝对速度方向判断。

习题3-4 取比例尺为mmm l 003.0=μ，作图如下1) 由图上可知：l l P P P P P v μωμω241442412224==，根据量得的长度，得s rad P P P P /455.414.72/14.32102414241224=⨯==ωω 可计算出C 点的速度为：s m CD v l C /4.0003.030455.44=⨯⨯==μω2) 构件1、3的瞬心在点13P 处，且为绝对瞬心，因此构件3的角速度为 ()s rad C P v l c /53.2)67.52003.0/(4.0133=⨯==μω 显然构件3上速度最小点在E 点，则其速度为s m EP v l E /36.0003.04.4753.2133=⨯⨯==ω3) 要使0=C v ，需瞬心12P 、24P 重合(如图)，两位置分别为0126'=∠=DAB ϕ，02227''=∠=DAB ϕ。

第二章习题解答习题2.2.4a) b) c) 习题2.2.9a) 对|w|作归纳法。

当|w|=1时w 为一字符，由题设已成立。

设),(ˆ),(ˆ0w q w q fδδ=， 则对任一字母a ，有 ).,(ˆ)),,(ˆ(ˆ)),,(ˆ(ˆ ),(ˆ00wa q a w q a w q wa q ff δδδδδδ=== b) 对k 作归纳法。

k=1时，由题设命题已成立。

设x k ∈ L(A)，即f k q x q =),(ˆ0δ。

于是 ff k k q x q x x q x q ===+),(ˆ)),,(ˆ(ˆ ),(ˆ010δδδδ，即x k ＋1∈ L(A)，证毕。

习题2.2.101) 将DFA 改写成转移图形式：2）观察上图，知其接受的语言应为L ＝{ w ∈{0,1}*: w 含奇数个1 }. 3) 用数学归纳法证明2）中的断言：当|w|=1时，若w ＝0则DFA 不接受w ，若w ＝1则DFA 接受w ，此时命题成立。

设w 时命题成立，即当w 中含偶数个1时DFA 不接受w ，当w 中含奇数个1时DFA 接受w 。

0,10,1对于任一字符c ：若c=0，则当w 中含偶数个1时由于DFA 不接受w ，故A w q =),(ˆ0δ，从而A wc q =),(ˆ0δ；当w 中含奇数个1时由于DFA 接受w ，故B w q =),(ˆ0δ，从而B wc q =),(ˆ0δ。

若c=1，则当w 中含偶数个1时由于DFA 不接受w ，故A w q =),(ˆ0δ，从而B wc q =),(ˆ0δ；当w 中含奇数个1时由于DFA 接受w ，故B w q =),(ˆ0δ，从而A wc q =),(ˆ0δ。

总之，当wc 中含偶数个1时DFA 不接受wc ，当wc 中含奇数个1时DFA 接受wc 。

命题得证。

习题2.2.111) 将DFA 改写成转移图形式：2）观察上图，知其接受的语言应为L ＝{ w ∈{0,1}*: w 不含子串00 }.3) 用数学归纳法证明2）中的断言，过程与前题类似。

形式语言与自动机课后作业答案第二章4．找出右线性文法，能构成长度为1 至5 个字符且以字母为首的字符串。

答：G={N,T,P,S}其中N={S,A,B,C,D} T={x,y} 其中x € {所有字母} y € {所有的字符} P 如下:S T x S T xA A f y A f yBB T y B T yC C T y C T yD D T y6．构造上下文无关文法能够产生L={ 3 / {a,b}*且3中a的个数是b的两倍}答：G={N,T,P,S}其中N={S} T={a,b} P 如下:S t aab S t aba S t baaS t aabS S t aaSb S t aSab S t SaabS t abaS S t abSa S t aSba S t SabaS t baaS S t baSa S t bSaa S t Sbaa7．找出由下列各组生成式产生的语言(起始符为S)(1) S t SaS S t b(2) S t aS b S t c(3) S T a S f aE aS答：(1) b(ab)n /n > 0}或者L二{(ba)n b/n > 0}(2) L={a n cb n /n > 0}(3) L={a2n+1 /n > 0}第三章1. 下列集合是否为正则集，若是正则集写出其正则式。

（1）含有偶数个a和奇数个b的{a,b}*上的字符串集合（2）含有相同个数a和b的字符串集合（3）不含子串aba的{a,b}*上的字符串集合答：（1）是正则集，自动机如下b b b b⑵不是正则集，用泵浦引理可以证明，具体见17题（2）（3）是正则集先看L '为包含子串aba的{a,b}*上的字符串集合显然这是正则集，可以写出表达式和画出自动机。

（略）则不包含子串aba的{a,b}*上的字符串集合L是L '勺非根据正则集的性质，L 也是正则集。