2018-2019学年度九年级数学上册 第一章 特殊平行四边形 1.3 正方形的性质与判定同步练习

1.3.1 正方形的性质与判定（1）教学目标知识与技能：了解正方形的有关概念，理解并掌握正方形的性质定理．过程与方法：经历探索正方形有关性质的过程，在观察中寻求新知，在探究中发展推理能力，逐步掌握说理的基本方法．情感态度与价值观：培养合情推理能力和探究习惯，体会平面几何的内在价值．重难点、关键重点：探索正方形的性质定理．难点：掌握正方形的性质的应用方法．关键：把握正方形既是矩形又是菱形这一特性来学习本节课内容．教学准备教师准备：投影仪，制作投影片，补充本节课内容，矩形纸片，活动的菱形框架．学生准备：复习平行四边形、矩形、菱形性质，预习本节课内容．学法解析1．认知起点：已积累了几何中平行四边形、矩形、菱形等知识，•在取得一定的经验的基础上，认知正方形．2．知识线索：3．学习方式：采用自导自主学习的方法解决重点，突破难点．教学过程一、合作探究，导入新课【显示投影片】显示内容：展示生活中有关正方形的图片，幻灯片（多幅）．【活动方略】教师活动：操作投影仪，边展示图片，边提出下面的问题：1．同学们观察显示的图片后，有什么联想？正方形四条边有什么关系？•四个角呢？ 2．正方形是矩形吗？是菱形吗？为什么？3．正方形具有哪些性质呢？学生活动：观察屏幕上所展示的生活中的正方形图片．进行联想．易知：1．•正方形四条边都相等（小学已学过）；正方形四个角都是直角（小学学过）．实验活动：教师拿出矩形按左图折叠．然后展开，让学生发现：只要矩形一组邻边相等，这样的矩形就是正方形；同样，教师拿出活动菱形框架，运动中让学生发现：只要菱形有一个内角为90°，这样的特殊菱形也是正方形．教师活动：组织学生联想正方形还具有哪些性质，板书画出一个正方形，如下图：学生活动：观察、联想到它是矩形，所以具有矩形的所有性质；它又是菱形，所以它又具有菱形的一切性质，归纳如下：正方形定义：有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形．正方形性质：（1）边的性质：对边平行，四条边都相等．（2）角的性质：四个角都是直角．（3）对角线的性质：两条对角线互相垂直平分且相等，•每条对角线平分一组对角．（4）对称性：是轴对称图形，有四条对称轴．【设计意图】采用合作交流、发现、归纳的方式来解决重点问题，突破难点．二、实践应用，探究新知【课堂演练】（投影显示）演练题1：如图，已知四边形ABCD是正方形，对角线AC与BD相交于O，MN∥AB，•且分别与OA、OB相交于M、N．求证：（1）BM=CN；（2）BM⊥CN．思路点拨：本题是证明BM=CN，根据正方形性质，可以证明BM、CN所在△BOM与△CON 是否全等．（2）在（1）的基础上完成，欲证BM⊥CN．只需证∠5+∠CMG=90°就可以了．【活动方略】教师活动：操作投影仪．组织学生演练，巡视，关注“学困生”；等待大部分学生练习做完之后，再请两位学生上台演示，交流．学生活动：课堂演练，相互讨论，解决演练题的问题．证：（1）•∵四边形ABCD是正方形，∴∠COB=∠BOM=90°，OC=OB。

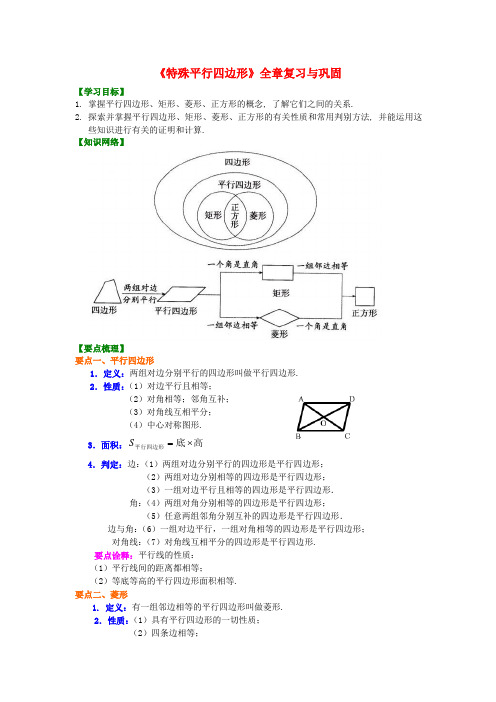
《特殊平行四边形》全章复习与巩固【学习目标】1. 掌握平行四边形、矩形、菱形、正方形的概念, 了解它们之间的关系.2. 探索并掌握平行四边形、矩形、菱形、正方形的有关性质和常用判别方法, 并能运用这些知识进行有关的证明和计算.【知识网络】【要点梳理】要点一、平行四边形1．定义：两组对边分别平行的四边形叫做平行四边形.2．性质：（1）对边平行且相等；（2）对角相等；邻角互补；（3）对角线互相平分；（4）中心对称图形.3．面积：高底平行四边形⨯=S4．判定：边：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形．角：（4）两组对角分别相等的四边形是平行四边形；（5）任意两组邻角分别互补的四边形是平行四边形．边与角：（6）一组对边平行，一组对角相等的四边形是平行四边形；对角线：（7）对角线互相平分的四边形是平行四边形.要点诠释：平行线的性质：（1）平行线间的距离都相等；（2）等底等高的平行四边形面积相等.要点二、菱形1. 定义：有一组邻边相等的平行四边形叫做菱形.2．性质：（1）具有平行四边形的一切性质；（2）四条边相等；（3）两条对角线互相平分且垂直，并且每一条对角线平分一组对角；（4）中心对称图形，轴对称图形.3．面积：2对角线对角线高＝＝底菱形⨯⨯S 4．判定：（1）一组邻边相等的平行四边形是菱形；（2）对角线互相垂直的平行四边形是菱形；（3）四边相等的四边形是菱形.要点三、矩形1．定义：有一个角是直角的平行四边形叫做矩形.2．性质：（1）具有平行四边形的所有性质；（2）四个角都是直角；（3）对角线互相平分且相等；（4）中心对称图形，轴对称图形.3．面积：宽＝长矩形⨯S４．判定：（1) 有一个角是直角的平行四边形是矩形.（2）对角线相等的平行四边形是矩形.（3）有三个角是直角的四边形是矩形.要点诠释：由矩形得直角三角形的性质：（1）直角三角形斜边上的中线等于斜边的一半；（2）直角三角形中，30度角所对应的直角边等于斜边的一半．要点四、正方形1. 定义：四条边都相等，四个角都是直角的四边形叫做正方形.2．性质：（1）对边平行；（2）四个角都是直角；（3）四条边都相等；（4）对角线互相垂直平分且相等，对角线平分对角；（5) 两条对角线把正方形分成四个全等的等腰直角三角形；（6）中心对称图形，轴对称图形.3．面积：=S 正方形边长×边长＝12×对角线×对角线 4．判定：（1）有一个角是直角的菱形是正方形；（2）一组邻边相等的矩形是正方形；（3）对角线相等的菱形是正方形；（4）对角线互相垂直的矩形是正方形；（5）对角线互相垂直平分且相等的四边形是正方形；（6）四条边都相等，四个角都是直角的四边形是正方形.【典型例题】类型一、平行四边形1、已知，△ABC 中，∠BAC=45°，以AB 为腰以点B 为直角顶点在△ABC 外部作等腰直角三角形ABD ，以AC 为斜边在△ABC 外部作等腰直角三角形ACE ，连结BE 、DC ，两条线段相交于点F ，试猜想∠EFC 的度数并说明理由．。

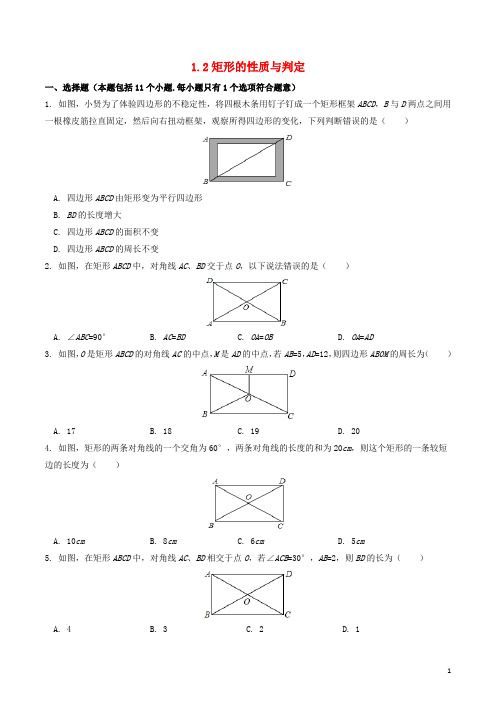
1.2矩形的性质与判定一、选择题（本题包括11个小题.每小题只有1个选项符合题意）1. 如图，小贤为了体验四边形的不稳定性，将四根木条用钉子钉成一个矩形框架ABCD，B与D两点之间用一根橡皮筋拉直固定，然后向右扭动框架，观察所得四边形的变化，下列判断错误的是（）A. 四边形ABCD由矩形变为平行四边形B. BD的长度增大C. 四边形ABCD的面积不变D. 四边形ABCD的周长不变2. 如图，在矩形ABCD中，对角线AC、BD交于点O，以下说法错误的是（）A. ∠ABC=90°B. AC=BDC. OA=OBD. OA=AD3. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=5，AD=12，则四边形ABOM的周长为（）A. 17B. 18C. 19D. 204. 如图，矩形的两条对角线的一个交角为60°，两条对角线的长度的和为20cm，则这个矩形的一条较短边的长度为（）A. 10cmB. 8cmC. 6cmD. 5cm5. 如图，在矩形ABCD中，对角线AC、BD相交于点O，若∠ACB=30°，AB=2，则BD的长为（）A. 4B. 3C. 2D. 16. 一个矩形被分成不同的4个三角形，其中绿色三角形的面积占矩形面积的15%，黄色的三角形的面积是212，则该矩形的面积为（）A. 602B. 702C. 1202D. 14027. 如图，矩形ABCD中，AC交BD于点O，∠AOD=60°，OE⊥AC．若AD=，则OE=（）A. 1B. 2C. 3D. 48. 矩形具有而菱形不具有的性质是（）A. 对角线相等B. 两组对边分别平行C. 对角线互相平分D. 两组对角分别相等9. 矩形的一内角平分线把矩形的一条边分成3cm和5cm的两部分，则此矩形的周长为（）A. 16cmB. 22cmC. 26cmD. 22cm或26cm10. 矩形的对角线所成的角之一是65°，则对角线与各边所成的角度是（）A. 57.5°B. 32.5°C. 57.5°，23.5°D. 57.5°，32.5°11. 过四边形的各个顶点分别作对角线的平行线，若这四条平行线围成一个矩形，则原四边形一定是（）A. 对角线相等的四边形B. 对角线垂直的四边形C. 对角线互相平分且相等的四边形D. 对角线互相垂直平分的四边形二、填空题（本题包括3个小题）12. 如图，平行四边形ABCD的对角线相交于点O，请你添加一个条件__________（只添一个即可），使平行四边形ABCD是矩形．13. 平行四边形ABCD的对角线相交于点O，分别添加下列条件：①∠ABC=90°；②AC⊥BD；③AB=BC；④AC 平分∠BAD；⑤AO=DO．使得四边形ABCD是矩形的条件有________14. 木工做一个长方形桌面，量得桌面的长为15cm，宽为8cm，对角线为17cm，这个桌面_________（填”合格”或”不合格”）三、解答题（本题包括5个小题）15. 如图，平行四边形ABCD中，点E、F、G、H分别在AB、BC、CD、AD边上且AE=CG，AH=CF．（1）求证：四边形EFGH是平行四边形；（2）如果AB=AD，且AH=AE，求证：四边形EFGH是矩形16. 如图，在△ABC中，AB=AC=5，BC=6，AD为BC边上的高，过点A作AE∥BC，过点D作DE∥AC，AE与DE交于点E，AB与DE交于点F，连结BE．求四边形AEBD的面积17. 如图，在平行四边形ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于点F，连接BE，∠F=45°．求证：四边形ABCD是矩形18. 有一块形状如图所示的玻璃，不小心把DEF部分打碎，现在只测得AB=60cm，BC=80cm，∠A=120°，∠B=60°，∠C=150°，你能设计一个方案，根据测得的数据求出AD的长吗？19. 如图，△ABC中，AB=AC，AD、AE分别是∠BAC与∠BAC的外角的平分线，BE⊥AE．求证：AB=DE答案一、选择题1. 【答案】C【解析】由题意可知，当向右扭动框架时，BD可伸长，故BD的长度变大，四边形ABCD由矩形变为平行四边形，因为四条边的长度不变，所以四边形ABCD的周长不变.原来矩形ABCD的面积等于BC乘以AB，变化后平行四边形ABCD的面积等于底乘以高，即BC乘以BC边上的高，BC边上的高小于AB，所以四边形ABCD 的面积变小了，故A,B,D说法正确，C说法错误.故正确的选项是C.考点：1.四边形面积计算；2.四边形的不稳定性.2. 【答案】D【解析】本题考查了矩形的性质；熟练掌握矩形的性质是解决问题的关键．矩形的性质：四个角都是直角，对角线互相平分且相等；由矩形的性质容易得出结论．∵四边形ABCD是矩形，∴∠ABC=∠BCD=∠CDA=∠BAD=90°，AC=BD，OA=AC，OB=BD，∴OA=OB，∴A、B、C正确，D错误考点：矩形的性质3. 【答案】D【解析】∵O是矩形ABCD的对角线AC的中点，M是AD的中点，∴∠ABC=∠D=90°，CD=AB=5，BC=AD=12，OA=OB，OM为△ACD的中位线，∴OM=CD=2.5，AC==13，∵O是矩形ABCD的对角线AC的中点，∴BO=AC=6.5,∴四边形ABOM的周长为AB+AM+BO+OM=5+6+6.5+2.5=20，故选D．考点：矩形的性质．4. 【答案】D【解析】∵四边形ABCD是矩形，∴OA=OC=AC，OD=OB=BD，AC=BD，∴OA=OB，∵AC+BD=20，∴AC=BD=10cm，∴OA=O B=5cm，∵OA=OB，∠AOB=60°，∴△OAB是等边三角形，∴AB=OA=5cm，故选D．考点：1．矩形的性质；2．等边三角形的判定与性质．5. 【答案】A【解析】在矩形ABCD中，∠ABC=90°，∵∠ACB=30°，AB=2，∴AC=2AB=2×2=4，∵四边形ABCD是矩形，∴BD=AC=4．故选A．6. 【答案】A【解析】黄色三角形与绿色三角形面积之和是矩形面积的50%，而绿色三角形面积占矩形面积的15%，所以黄色三角形面积占矩形面积的（50%-15%）=35%，已知黄色三角形面积是21平方厘米，故矩形的面积=21÷（50%-15%）=21÷35%=60（cm2）．故选A．考点：矩形的性质．7.【答案】A【解析】∵四边形ABCD是矩形，∠AOD=60°，∴△ADO是等边三角形，∴OA=，∠OAD=60°，∴∠OAE= 30°，∵OE⊥AC，∴△OAE是一个含30°的直角三角形，∴OE=1，故选A．8.【答案】A【解析】∵矩形具有的性质是：对角线相等且互相平分，两组对边分别平行，两组对角分别相等；菱形具有的性质是：两组对边分别平行，对角线互相平分，两组对角分别相等；∴矩形具有而菱形不具有的性质是：对角线相等．故选A．9. 【答案】D【解析】∵四边形ABCD是矩形，∴AD=BC，AB=CD，AD∥BC，∴∠AEB=∠CBE，∵BE平分∠ABC，∴∠ABE=∠CBE，∴∠AEB=∠ABE，∴AB=AE，当AE=3cm时，AB=AE=3=CD，AD=3cm+5cm=8cm=BC，∴此时矩形ABCD的周长是AB+BC+CD+AD=3cm+8cm+3cm+8cm=22cm；当AE=5cm时，AB=AE=5cm=CD，AD=3cm+5cm=8cm=BC，∴此时矩形ABCD的周长是AB+BC+CD+AD=5cm+8cm+5cm+8cm=26cm；故选D．考点：矩形的性质．10. 【答案】D【解析】∵四边形ABCD是矩形，∴∠ABC=90°，AD∥BC，AB∥CD，AC=BD，AO=OC，OB=OD，∴OB=OA=OC=OD，∠OAB=∠OCD，∠DAO=∠OCB，∴∠OAD=∠ODA，∠OCB=∠OBC，∠ODC=∠OCD，∠OAB=∠OBA=×（180°﹣∠AOB）=×（180°﹣65°）=57.5°，∵∠ABC=90°，∴∠ACB=90°﹣57.5°=32.5°，即∠OAD=∠ODA=∠OBC=∠OCB=32.5°，∠OAB=∠OBA=∠ODC=∠OCD=57.5°，对角线与各边所成的角度是57.5°和32.5°，故选D．点睛：本题考查了矩形的性质，三角形的内角和定理，等腰三角形的性质的应用，能正确运用矩形的性质进行推理是解此题的关键，注意：矩形的对角线相等且互相平分．11. 【答案】B【解析】∵四边形EFGH是矩形，∴∠E=90°，∵EF∥AC，EH∥BD，∴∠E+∠EAG=180°，∠E+∠EBO=180°，∴∠EAO=∠EBO=90°，∴四边形AEBO是矩形，∴∠AOB=90°，∴AC⊥BD，故选B．二、填空题12. 【答案】AC=BD．答案不唯一【解析】添加的条件是AC=BD，理由是：∵AC=BD，四边形ABCD是平行四边形，∴平行四边形ABCD是矩形，故答案为：AC=BD．答案不唯一．点睛：本题考查了矩形的判定定理的应用，注意：对角线相等的平行四边形是矩形，此题是一道开放型的题目，答案不唯一．13.【答案】①⑤【解析】要使得平行四边形ABCD为矩形添加：①∠ABC=90°；⑤AO=DO2个即可；故答案为：①⑤．14. 【答案】合格【解析】勾股定理的逆定理：若一个三角形的两边长的平方和等于第三边的平方，则这个三角形的直角三角形.∵∴这个桌面合格.考点：勾股定理的逆定理点评：本题属于基础应用题，只需学生熟练掌握勾股定理的逆定理，即可完成.三、解答题15. 【答案】（1）证明见解析；（2）证明见解析.【解析】（1）易证得△AEH≌△CGF，从而证得BE=DG，DH=BF．故有，△BEF≌△DGH，根据两组对边分别相等的四边形是平行四边形而得证．（2）由题意知，平行四边形ABCD是菱形，连接AC，BD，则有AC⊥B D，由AB=AD，且AH=AE可证得HE∥BD，同理可得到HG∥AC，故HG⊥HE，又由（1）知四边形HGFE是平行四边形，故四边形HGFE是矩形．证明：（1）在平行四边形ABCD中，∠A=∠C，又∵AE=CG，AH=CF，∴△AEH≌△CGF．∴EH=GF．在平行四边形ABCD中，AB=CD，AD=BC，∴AB-AE=CD-CG，AD-AH=BC-CF，即BE=DG，DH=BF．又∵在平行四边形ABCD中，∠B=∠D，∴△BEF≌△DGH．∴GH=EF．∴四边形EFGH是平行四边形．（2）在平行四边形ABCD中，AB∥CD，AB=CD．设∠A=α，则∠D=180°-α．∵AE=AH，∴∠AHE=∠AEH=．∵AD=AB=CD，AH=AE=CG，∴AD-AH=CD-CG，即DH=DG．∴∠DHG=∠DGH=．∴∠EHG=180°-∠DHG-∠AHE=90°．又∵四边形EFGH是平行四边形，∴四边形EFGH是矩形．考点：1.矩形的判定与性质；2.全等三角形的判定与性质；3.平行四边形的判定与性质．16. 【答案】12.【解析】利用平行四边形的性质和矩形的判定定理推知平行四边形AEBD是矩形．在Rt△ADC中，由勾股定理可以求得AD的长度，由等腰三角形的性质求得CD（或BD）的长度，则矩形的面积=长×宽=AD•BD=AD•CD．解：∵AE∥BC，BE∥AC，∴四边形AEDC是平行四边形，∴AE=CD．在△ABC中，AB=AC，AD为BC边上的高，∴∠ADB=90°，BD=CD，∴BD=AE，∴平行四边形AEBD是矩形．在Rt△ADC中，∠ADB=90°，AC=5，CD=BC=3，∴AD==4，∴四边形AEBD的面积为：BD•AD=CD•AD=3×4=12．点睛：本题考查了矩形的判定与性质和勾股定理，根据“等腰三角形的性质和有一内角为直角的平行四边形为矩形”推知平行四边形AEBD是矩形是解题的难点．17. 【答案】证明见解析.【解析】欲证明四边形ABCD是矩形，只需推知∠DAB是直角．证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAF=∠F.∵∠F=45°，∴∠DAE=45°．∵AF是∠BAD的平分线，∴∠EAB=∠DAE=45°，∴∠DAB=90°．又∵四边形ABCD是平行四边形，∴四边形ABCD是矩形．18. 【答案】AD＝140cm．【解析】过C作CM∥AB，交AD于M，推出平行四边形ABCM，推出AM=BC=80cm，AB=CM=60cm，∠B=∠AMC，求出∠D=∠MCD，求出CM=DM=60cm，代入AD=AM+DM求出即可．解：过C作CM∥AB，交AD于M，∵∠A=120°，∠B=60°，∴∠A+∠B=180°，∴AM∥BC，∵AB∥CM，∴四边形ABCM是平行四边形，∴AB=CM=60cm，BC=AM=80cm，∠B=∠AMC=60°，∵AD∥BC，∠C=150°，∴∠D=180°﹣150°=30°，∴∠MCD=60°﹣30°=30°=∠D，∴CM=DM=60cm，∴AD=60cm+80cm=140cm．19. 【答案】证明见解析.【解析】先由角平分线和等腰三角形的性质证明AE∥BD，再由AD、AE分别是∠BAC与∠BAC的外角的平分线可证得DA⊥AE，可得AD∥BE，可证得四边形ADBE为矩形，可得结论．证明：∵AD、AE分别是∠BAC与∠BAC的外角的平分线，∴∠BAD+∠EAB=（∠BAC+∠FAB）=90°，∵BE⊥AE，∴DA∥BE，∵AB=AC，∴∠ABC=∠ACB，∵∠FAB=∠ABC+∠ACB=2∠ABC，且∠FAB=2∠EAB，∴∠ABC=∠EAB，∴AE∥BD，∴四边形AEBD为平行四边形，且∠BEA=90°，∴四边形AEBD为矩形，∴AB=DE．点睛：本题主要考查矩形的判定和性质，由角平分线及等腰三角形的性质证明AE∥BD是解题的关键．。

正方形【学习目标】1．理解正方形的观点，认识平行四边形、矩形及菱形与正方形的观点之间的附属关系；2．掌握正方形的性质及判断方法．【重点梳理】重点一、正方形的定义四条边都相等，四个角都是直角的四边形叫做正方形.重点解说：既是矩形又是菱形的四边形是正方形，它是特别的菱形，又是特别的矩形，更加特别的平行四边形，正方形是有一组邻边相等的矩形，仍是有一个角是直角的菱形.重点二、正方形的性质正方形拥有四边形、平行四边形、矩形、菱形的全部性质.1.边——四边相等、邻边垂直、对边平行；2.角——四个角都是直角；3.对角线——①相等，②相互垂直均分，③每条对角线均分一组对角；4. 是轴对称图形，有 4 条对称轴；又是中心对称图形，两条对角线的交点是对称中心重点解说：正方形拥有平行四边形、矩形、菱形的全部性质，其对角线将正方形分为四个等腰直角三角形.重点三、正方形的判断正方形的判断除定义外，判断思路有两条：或先证四边形是菱形，再证明它有一个角是直角或对角线相等（即矩形）；或先证四边形是矩形，再证明它有一组邻边相等或对角线互相垂直（即菱形）..重点四、特别平行四边形之间的关系或许可表示为：重点五、按序连结特别的平行四边形各边中点获得的四边形的形状（ 1）按序连结平行四边形各边中点获得的四边形是平行四边形.（ 2）按序连结矩形各边中点获得的四边形是菱形.（ 3）按序连结菱形各边中点获得的四边形是矩形.（ 4）按序连结正方形各边中点获得的四边形是正方形.重点解说：新四边形由原四边形各边中点按序连结而成.（ 1）若原四边形的对角线相互垂直，则新四边形是矩形（ 2）若原四边形的对角线相等，则新四边形是菱形.（ 3）若原四边形的对角线垂直且相等，则新四边形是正方形..【典型例题】种类一、正方形的性质1、已知：如图，在正方形ABCD中，点 E 在边 CD上， AQ⊥BE 于点 Q，DP⊥AQ 于点 P．（1）求证： AP=BQ；（2）在不增添任何协助线的状况下，请直接写出图中四对线段，使每对中较长线段与较短线段长度的差等于 PQ的长．【思路点拨】（1）依据正方形的性质得出AD=BA，∠ BAQ=∠ADP，再依据已知条件获得∠AQB=∠DPA，判断△ AQB≌△ DPA 并得出结论；（ 2）依据 AQ﹣ AP=PQ和全等三角形的对应边相等进行判断剖析．【答案与分析】解：（ 1）∵正方形ABCD∴A D=BA，∠ BAD=90°，即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ ADP+∠DAP=90°∴∠ BAQ=∠ADP∵AQ⊥BE 于点 Q，DP⊥AQ 于点 P∴∠ AQB=∠DPA=90°∴△ AQB≌△ DPA（ AAS）∴AP=BQ（2）① AQ﹣ AP=PQ②AQ﹣ BQ=PQ③DP﹣ AP=PQ④DP﹣ BQ=PQ【总结升华】此题主要观察了正方形以及全等三角形，解决问题的重点是掌握：正方形的四条边相等，四个角都是直角．解题时需要运用：有两角和此中一角的对边对应相等的两个三角形全等，以及全等三角形的对应边相等．贯通融会：【变式 1】如图四边形ABCD是正方形，点E、 K 分别在 BC， AB 上，点 G在 BA的延伸线上，且 CE＝ BK＝AG．以线段 DE、 DG为边作正方形 DEFG．(1)求证： DE＝ DG，且 DE⊥DG．(2)连结 KF，猜想四边形 CEFK是如何的特别四边形，并证明你的猜想．【答案】证明： (1) ∵四边形ABCD是正方形，∴DC ＝ DA，∠ DCE＝∠ DAG＝90°．又∵ CE ＝ AG，∴△DCE≌△ DAG，∴∠EDC＝∠ GDA， DE＝ DG．又∵∠ADE＋∠ EDC＝90°，∴∠ADE＋∠ GDA＝90°，∴ DE ⊥DG．(2)四边形 CEFK为平行四边形．证明：设 CK， DE订交于 M点，∵四边形 ABCD和四边形 DEFG都是正方形，∴ AB ∥CD， AB＝ CD，EF＝ DG，EF∥DG；∵BK ＝ AG，∴ KG ＝ AB＝ CD．∴四边形CKGD为平行四边形．∴CK ＝ DG＝EF，CK∥DG∥EF∴四边形 CEFK为平行四边形．O1、O2是此中两个正方形的中心，【变式 2】如图，三个边长均为 2 的正方形重叠在一同，则暗影部分的面积是_______．【答案】 2；提示：暗影部分面积等于正方形面积的一半.种类二、正方形的判断2、如图，在 Rt△ABC中，∠ BAC=90°， AD=CD，点 E 是边 AC的中点，连结 DE， DE的延伸线与边 BC订交于点 F，AG∥BC，交 DE于点 G，连结 AF、 CG．（1）求证： AF=BF；（2）假如 AB=AC，求证：四边形 AFCG是正方形．【思路点拨】（1）依据线段垂直均分线的性质，可得AF=CF，再依据等角的余角相等可得∠B=∠BAF，因此 AF=BF．（2）由 AAS可证△ AEG≌△ CEF，因此 AG=CF．由一组对边平行且相等的四边形是平行四边形得四边形 AFCG是平行四边形，从而证得四边形 AFCG是菱形，最后依占有一个角为直角的菱形是正方形得证四边形 AFCG是正方形．【答案与分析】证明：（ 1）∵ AD=CD，点 E 是边 AC的中点，∴DE⊥AC．即得 DE是线段 AC的垂直均分线．∴A F=CF．∴∠ FAC=∠ACB．在 Rt△ABC中，由∠ BAC=90°，得∠ B+∠ACB=90°，∠ FAC+∠BAF=90°．∴∠ B=∠BAF．∴A F=BF．（2）∵ AG∥CF，∴∠ AGE=∠CFE．又∵点 E 是边 AC的中点，∴AE=CE．在△ AEG和△ CEF中，，∴△ AEG≌△ CEF（ AAS）．∴AG=CF．又∵ AG∥CF，∴四边形AFCG是平行四边形．∵A F=CF，∴四边形 AFCG是菱形．在 Rt△ABC中，由 AF=CF， AF=BF，得 BF=CF．即得点 F 是边 BC的中点．又∵ AB=AC，∴ AF⊥BC．即得∠AFC=90°．∴四边形 AFCG是正方形．【总结升华】此题观察的是正方形的判断方法，观察了线段垂直均分线的性质、全等三角形的判断与性质等基础知识的灵巧运用，鉴别一个四边形是正方形主假如依据正方形的定义及其性质．贯通融会：【变式】如图，矩形 ABCD中， AD=6，DC=8，菱形 EFGH的三个极点 E，G，H分别在矩形 ABCD 的边 AB， CD， DA上， AH=2，连结 CF．（1）若 DG=2，求证：四边形 EFGH为正方形；（2）若 DG=6，求△ FCG的面积．【答案】（1）证明：∵四边形 EFGH为菱形，∴HG=EH，∵AH=2， DG=2，∴DG=AH，在 Rt△DHG和△ AEH中，，∴Rt△DHG≌△ AEH，∴∠ DHG=∠AEH，∵∠AEH+∠AHG=90°，∴∠DHG+∠AHG=90°，∴∠GHE=90°，∵四边形EFGH为菱形，∴四边形EFGH为正方形；（2）解：作 FQ⊥CD于 Q，连结 GE，如图，∵四边形 ABCD为矩形，∴AB∥CD，∴∠ AEG=∠QGE，即∠ AEH+∠HEG=∠QGF+∠FGE，∵四边形 EFGH为菱形，∴HE=GF，HE∥GF，∴∠ HEG=∠FGE，∴∠ AEH=∠QGF，在△ AEH和△ QGF中，∴△ AEH≌△ QGF，∴A H=QF=2，∵DG=6， CD=8，∴C G=2，∴△ FCG的面积 = CG?FQ= ×2×2=2．种类三、正方形综合应用3、E、 F 分别是正方形ABCD的边 AD和 CD上的点，若∠ EBF＝45°．(1)求证： AE＋ CF＝ EF．(2) 若 E 点、 F 点分别是边DA、 CD的延伸线上的点，结论（1）仍建立吗？若建立，请证明，若不建立，写出正确结论并加以证明．【答案与分析】证明：（ 1）延伸 DC，使 CH＝AE，连结 BH，∵四边形ABCD是正方形，∴∠A＝∠ BCH＝90°，又AB＝ BC， CH＝ AE，∴Rt △BAE≌Rt△BCH，∴∠1＝∠ 2， BE＝ BH．在又∵∠1＋∠ 3＋∠ 4＝90°，∠ 4＝45°，∴ ∠1＋∠ 3＝45°，∠ 2＋∠ 3＝45°，△EBF 和△HBF中，∴△EBF≌△ HBF，∴EF ＝ FH＝ FC＋ CH＝ AE＋ CF．即 AE＋ CF＝ EF．(2)如下图：不建立，正确结论： EF＝ CF－ AE．证明：在 CF上截取 CH＝ AE，连结 BH．∵四边形 ABCD是正方形，∴在 Rt△EAB 和 Rt△HCB中，∴Rt △EAB≌Rt△HCB，∴BE ＝ BH，∠ EBA＝∠ HBC．∵∠HBC ＋∠ ABH＝90°，∴∠EBA＋∠ ABH＝90°．又∵∠EBF＝45°，∴∠HBF＝45°，即∠ EBF＝∠ HBF．在△ EBF 和△ HBF中∴△EBF≌△ HBF，∴EF ＝ FH＝ CF－ CH＝ CF－ AE，即 EF＝ CF－ AE．【总结升华】此题主要观察正方形的性质，全等三角形的性质和判断，重点在于用“截长补短”的方法正确地作出协助线 .4、正方形ABCD的对角线交点为 O，如下图， AE均分∠B AC交 BC于 E，交 OB于 F，求证：EC＝2FO．【思路点拨】在平面几何中，要证明一条线段等于另一条线段的2倍或，往常采纳折半法或加倍法．而折半法又可分直接折半法和间接折半法；加倍又可分直接加倍法和间接加倍法．这就需要学生认真研究，找到解决问题的适合方法．【答案与分析】证法一： ( 间接折半法 ) 如图①所示．∵∠3＝∠ 1＋∠ 4，∠ 5＝∠ 2＋∠ 6．而∠ 1＝∠ 2，∠ 4＝∠ 6＝45°．∴∠3＝∠ 5， BE＝ BF．取 AE的中点 G，连结 OG，∵AO＝OC，∴OG EC．由∠ 7＝∠ 5，∠ 8＝∠ 3，∴∠7＝∠ 8，∴ FO ＝ GO．∴EC ＝ 2OG＝ 2FO．证法二： ( 直接折半法 ) 如图②所示．由证法一得BE＝ BF．取 EC的中点 H，连结 OH．∵ AO ＝ OC，∴ OH∥AE．∴ ∠BOH＝∠ BFE＝∠ BEF＝∠ BHO．∴ BO ＝ BH，∴ FO ＝EH．∴ EC ＝ 2EH＝ 2FO．证法三： ( 直接加倍法 ) 如图③所示．由证法一得 BE＝ BF．在 OD上截取 OM＝ OF，连结 MC．易证Rt△AOF≌Rt△COM．∴∠OAF＝∠ OCM，∴ AE ∥MC．由∠ BMC＝∠ BFE＝∠ BEF＝∠BCM，∴ FM＝ EC．∴EC ＝ FM＝ 2FO．【总结升华】若题目中波及线段的倍半关系和中点问题时，要联想中位线定理，利用中点构造中位线，要注意从不一样的角度进行思构，结构不一样的协助线来解决问题．贯通融会：【变式】在正方形ABCD的边 AB上任取一点 E，作 EF⊥AB 交 BD于点 F，取 FD的中点 G，连接 EG、 CG，如图①，易证 EG＝ CG，且 EG⊥CG．(1)将△ BEF 绕点 B 逆时针旋转 90°，如图②，则线段 EG和 CG有如何的数目关系和位置关系 ?请直接写出你的猜想．(2)将△ BEF 绕点 B 逆时针旋转 180°，如图③，则线段 EG和 CG又有如何的数目关系和地点关系 ?请写出你的猜想，并加以证明．【答案】解： (1)EG＝ CG，且 EG⊥CG．(2)EG＝ CG，且 EG⊥CG．证明：延伸FE 交 DC延伸线于M，连 MG，如图③，∵∠AEM＝90°，∠ EBC＝90°，∠ BCM＝90°，∴四边形BEMC是矩形．∴BE ＝ CM，∠ EMC＝90°，又∵ BE ＝ EF，∴ EF ＝CM．∵ ∠EMC＝90°， FG＝DG，∴ MG＝FD＝ FG．∵BC ＝ EM， BC＝ CD，∴ EM＝ CD．∵ EF ＝ CM，∴ FM ＝ DM，∴∠F＝45°．2018-2019学年九年级数学上册第一章特殊平行四边形3正方形的性质与判定知识讲解例题演练北师大版又 FG＝ DG，∠ CMG＝∠EMD＝45°，∴∠F＝∠ GMC，∴△GFE≌△ GMC，∴EG ＝ CG，∠ FGE＝∠MGC，∵ MG⊥DF，∴∠FGE＋∠ EGM＝90°，∴∠MGC＋∠ EGM＝90°即∠ EGC＝90°，∴EG ⊥CG．。

注意知识间联系巧学正方形判定在学习正方形的判定时,很多同学对正方形的判定感觉无从下手，更有甚者，将判定方法死记硬背，结果背的很“熟”,但真正用起来时还是不会．其实，正方形的判定这一小节是前面几节课的小结,只要将知识间的联系弄明白了,问题也就迎刃而解了．一、知识结构图只要在头脑中构建出了良好的知识结构图，相信这部分内容对你来说已不在话下了．二、练习广角1．下列命题中：①如果一个菱形的两条对角线相等,那么它一定是正方形；②如果一个矩形的两条对角线互相垂直，那么它一定是正方形；③两条对角线互相垂直且相等的四边形一定是正方形；④四条边相等，且有一个角是直角的四边形是正方形．其中，真命题有___________个．2．已知：点E、F、G、H分别是正方形ABCD四条边的中点．问：四边形EFGH是什么样的图形？若将条件改为:AE=BF=CG=DH，如下图,结论还成立吗?若将正方形ABCD改为矩形，结论还成立吗？3．在△ABC中，CD是∠ACB的平分线，DE⊥BC，DF⊥AC，垂足分别为E、F．要使四边形CEDF是正方形需添加什么条件？并说明你的理由．答案与提示：1．3．（①②④是真命题．）2．四边形EFGH是正方形；若将条件改为(易证△EFH、△FGE、△GHF、△HEG是全等的等腰直角三角形,从而结论也就得出来了）：AE=BF=CG=DH，结论还成立；若将正方形ABCD改为矩形，结论不成立，所得四边形是菱形．3．∠ACB＝90°．（由∠ACB＝90°、DE⊥BC、DF⊥AC可证明四边形CEDF是矩形，而后根据角平分线的性质得DE＝DF，从而证明结论成立．)尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

九年级数学上册第一章特殊平行四边形3 正方形的性质与判定注意知识间联系,巧学正方形判定素材（新版)北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学上册第一章特殊平行四边形3 正方形的性质与判定注意知识间联系,巧学正方形判定素材(新版）北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉,前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步，以下为九年级数学上册第一章特殊平行四边形3 正方形的性质与判定注意知识间联系,巧学正方形判定素材(新版）北师大版的全部内容。

注意知识间联系巧学正方形判定在学习正方形的判定时,很多同学对正方形的判定感觉无从下手，更有甚者，将判定方法死记硬背,结果背的很“熟”,但真正用起来时还是不会.其实，正方形的判定这一小节是前面几节课的小结,只要将知识间的联系弄明白了,问题也就迎刃而解了．一、知识结构图只要在头脑中构建出了良好的知识结构图,相信这部分内容对你来说已不在话下了．二、练习广角1.下列命题中：①如果一个菱形的两条对角线相等,那么它一定是正方形；②如果一个矩形的两条对角线互相垂直,那么它一定是正方形;③两条对角线互相垂直且相等的四边形一定是正方形;④四条边相等，且有一个角是直角的四边形是正方形．其中，真命题有____＿_＿__＿_个.2.已知：点E、F、Ｇ、Ｈ分别是正方形ＡBCD四条边的中点．问：四边形EFGH是什么样的图形？若将条件改为:AE＝BF=CＧ＝DH,如下图,结论还成立吗?若将正方形ABCＤ改为矩形,结论还成立吗？３.在△AＢC中,CD是∠ACＢ的平分线,ＤE⊥BC，ＤF⊥AC,垂足分别为E、F.要使四边形CＥDＦ是正方形需添加什么条件？并说明你的理由.答案与提示:１.３．(①②④是真命题.）2.四边形ＥFGＨ是正方形;若将条件改为(易证△EFH、△FGE、△GＨF、△HEG是全等的等腰直角三角形,从而结论也就得出来了)：AE＝BF=CＧ=ＤH，结论还成立；若将正方形ABＣD改为矩形，结论不成立，所得四边形是菱形．3．∠ACB＝90°．(由∠ACB＝９０°、DE⊥BC、DF⊥AＣ可证明四边形ＣEDＦ是矩形,而后根据角平分线的性质得DE=ＤF，从而证明结论成立．)以上就是本文的全部内容，可以编辑修改。

九年级数学上册第一章特殊平行四边形3 正方形的性质与判定矩形、菱形、正方形错例辨析素材(新版）北师大版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望(九年级数学上册第一章特殊平行四边形 3 正方形的性质与判定矩形、菱形、正方形错例辨析素材（新版)北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉,前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为九年级数学上册第一章特殊平行四边形 3 正方形的性质与判定矩形、菱形、正方形错例辨析素材（新版）北师大版的全部内容。

矩形、菱形、正方形错例辨析在初学矩形、菱形、正方形这部分内容时，由于对这几个图形的性质和判定掌握不够好,常出现这样或那样的错误，现举例辨析，供学习时参考．例1 两条对角线相等的四边形是( )Ａ．平行四边形Ｂ．菱形C.矩形D.不能确定错解:选C.辨析：两条对角线相等的图形不一定是矩形,如图1,可以是不规则的四边形,图中对角线AC=BD.正解:选D．例2 对角线____＿__＿_＿_＿＿的四边形是菱形.错解:互相垂直.辨析：对角线互相垂直的四边形不一定是菱形，如图２就不是菱形，应强调垂直且互相平分．正解：垂直且互相平分．例3 正方形ABCD中，两条对角线的交点为O，∠BAＣ的平分线交BD于Ｅ,若正方形的边长是2ｃｍ，则DE的长是（)Ａ．1cm ﻩB.２cmﻩＣ.3cmﻩﻩD.32cm2错解:选D.辨析：如图3，把E 当作OB 的中点，这样由勾股定理可以算出222222BD =+=(c ｍ）,1322222DE OD OE =+=+=（cm),这是错误的. 本题应先推出∠DA Ｅ=∠DE Ａ(∠EAD =∠OAD +∠OAE =67。