下载文档原格式
概率论与数理统计教学教案 第2章 随机变量及其分布授课序号01教 学 基 本 内 容一．随机变量1. 随机变量：设E 是随机试验，样本空间为S ，如果对随机试验的每一个结果ω，都有一个实数()X ω与之对应，那么把这个定义在S 上的单值实值函数()X X ω=称为随机变量．随机变量一般用大写字母,,X Y Z ,…表示．2.随机变量的两种常见类型:离散型随机变量和连续型随机变量. 二．分布函数1. 分布函数：设X 是一个随机变量，x 是任意实数，称函数{}(),F x P X x x =≤-∞<<∞为随机变量X 的分布函数，显然，()F x 是一个定义在实数域R 上，取值于[0,1]的函数．2．几何意义：在数轴上，将X 看成随机点的坐标，则分布函数()F x 表示随机点X 落在阴影部分（即X x ≤）内的概率，如下图．3．对任意的实数,,()a b c a b <，都有：授课序号02(,)B n p ，其中在二项分(1,)B p X 服从（0-1）分布是二项分布的特例，简记0,1,2,...，其中λ为大于()P λ．在一次试验中出现的概率为(12,kk nnC p p -.）说明：泊松定理表明，泊松分布为二项分布的极限分布，即在试验次数很大，而n np 不太大时，()G p．）说明：几何分布描述的是试验首次成功的次数次才取得第一次成功，前）超几何分布：若随机变量X的分布律为H n N(,,件不合格，从产品中不放回）超几何分布与二项分布之间的区别：超几何分布是不放回抽取，二项分布是放回抽取，因此，二项两个分布之间也有联系，当总体的容量授课序号03(,)U a b ．内的任一个子区间()E λ．1,0,xe x λ-⎧->⎪⎨⎪⎩其它.）定理：（指数分布的无记忆性）设随机变量()E λ，则对于任意的正数{}{P X s t t P X >+>=为连续型随机变量，若概率密度为2(,N μσ处取到最大值，并且对于同样长度（iii ）当参数μ固定时，σ的值越大，()f x 的图形就越平缓；σ的值越小，()f x 的图形就越尖狭，由此可见参数σ的变化能改变图形的形状，称σ为形状参数．（iv ）当参数σ固定时，随着μ值的变化，()f x 图形的形状不改变，位置发生左右平移，由此可见参数μ的变化能改变图形的位置，称μ为位置参数．（4）标准正态分布(0,1)XN（i ）概率密度221(),2x x e x ϕπ-=-∞<<∞（ii ）分布函数221(),.2t xx e dt x π--∞Φ=-∞<<∞⎰（iii ）根据概率密度()x ϕ的对称性，有()1().x x Φ-=-Φ （5）定理：（标准化定理）若2(,)XN μσ，则(0,1).X Z N μσ-=（6）标准化定理的应用：设,,()x a b a b <为任意实数，则(){}{}{}(),X x x x F x P X x P P Z μμμμσσσσ----=≤=≤=≤=Φ{}{}()().a X b b a P a X b P μμμμμσσσσσ-----<≤=<≤=Φ-Φ6.“3σ”法则：设2(,)XN μσ，则{33}(3)(3)2(3)10.997,P X μσμσ-<<+=Φ-Φ-=Φ-≈即正态分布2(,)N μσ的随机变量以99.7%的概率落在以μ为中心、3σ为半径的区间内，落在区间以外的概率非常小，可以忽略不计，这就是“3σ”法则. 三．例题讲解例1．车流中的“时间间隔”是指一辆车通过一个固定地点与下一辆车开始通过该点之间的时间长度.设X 表示在大流量期间，高速公路上相邻两辆车的时间间隔，X 的概率密度描述了高速公路上的交通流量规律，其表达式为：0.15(0.5)0.15,0.5,()0,x e x f x --⎧≥⎪=⎨⎪⎩其它.概率密度()f x 的图形如下图，求时间间隔不大于5秒的概率.例2．设随机变量X 表示桥梁的动力荷载的大小（单位:N ），其概率密度为13,02;()880,x x f x ⎧+≤≤⎪=⎨⎪⎩其它.求：（1）分布函数()F x ；（2）概率{1 1.5}P X ≤≤及{1}P X >.例3．某食品厂生产一种产品，规定其重量的误差不能超过3克，即随机误差X 服从（-3,3）上的均匀分布.现任取出一件产品进行称重，求误差在-1~2之间的概率.例4．设随机变量X 在（1,4）上服从均匀分布，对X 进行三次独立的观察，求至少有两次观察值大于2的概率.例5.设随机变量X 表示某餐馆从开门营业起到第一个顾客到达的等待时间（单位：min ），则X 服从指数分布，其概率密度为0.40.4,0,()0,xex f x -⎧>⎪=⎨⎪⎩其它.求等待至多5分钟的概率以及等待3至4分钟的概率.例6．汽车驾驶员在减速时，对信号灯做出反应所需的时间对于帮助避免追尾碰撞至关重要．有研究表明，驾驶员在行车过程中对信号灯发出制动信号的反应时间服从正态分布，其中μ=1.25秒，σ=0.46秒．求驾驶员的制动反应时间在1秒至1.75秒之间的概率？如果2秒是一个非常长的反应时间，那么实际的制动反应时间超过这个值的概率是多少？例7．设某公司制造绳索的抗断强度服从正态分布，其中μ=300千克，σ=24千克.求常数a ，使抗断强度以不小于95%的概率大于a .授课序号0450。
随机变量及其概率分布随机变量是概率论和数理统计中的重要概念，描述了随机事件的数值特征。
概率分布则用于描述随机变量取值的概率情况。
本文将介绍随机变量及其概率分布的基本概念和常见的概率分布模型。
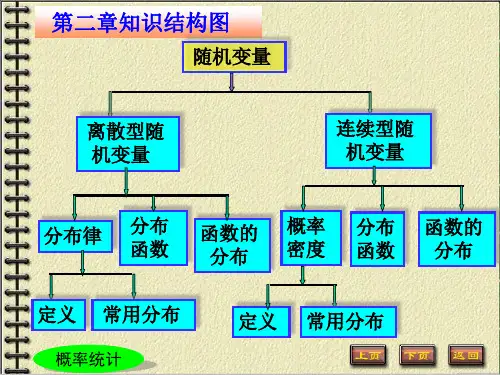
一、随机变量的定义与分类随机变量是对随机事件结果的数值化描述。
随机变量可分为离散型随机变量和连续型随机变量两种。
1. 离散型随机变量离散型随机变量只能取有限个或可数个值，常用字母X表示。
例如，抛掷骰子的点数就是一个离散型随机变量，可能取1、2、3、4、5、6之一。
2. 连续型随机变量连续型随机变量可以取某个区间内的任意值，通常用字母Y表示。
例如，测量某个物体长度的随机误差就可看作是一个连续型随机变量。
二、概率分布的概念与性质概率分布描述了随机变量取值的概率情况。
常见的概率分布包括离散型分布和连续型分布。
1. 离散型概率分布离散型概率分布描述了离散型随机变量取值的概率情况。
离散型概率分布函数可以用概率质量函数（probability mass function，PMF）来表示。
PMF表示了随机变量取某个特定值的概率。
离散型概率分布函数具有以下性质：①非负性，即概率大于等于0；②归一性，即所有可能取值的概率之和等于1。
常见的离散型概率分布有：伯努利分布、二项分布、几何分布、泊松分布等。
2. 连续型概率分布连续型概率分布描述了连续型随机变量取值的概率情况。
连续型概率分布函数可以用概率密度函数（probability density function，PDF）来表示。
PDF表示在随机变量取某个特定值附近的概率密度。
连续型概率分布函数具有以下性质：①非负性；②积分为1。
常见的连续型概率分布有：均匀分布、正态分布、指数分布等。
三、常见的1. 伯努利分布伯努利分布描述了一次随机试验中两个互斥结果的概率情况，取值为0或1。
其概率质量函数为：P(X=k) = p^k * (1-p)^(1-k)，k=0或1其中，p为成功的概率，1-p为失败的概率。
概率论与数理统计教案-随机变量及其分布一、教学目标1. 了解随机变量的概念及其重要性。
2. 掌握随机变量的分布函数及其性质。
3. 学习离散型随机变量的概率分布及其数学期望。
4. 理解连续型随机变量的概率密度及其数学期望。
5. 能够运用随机变量及其分布解决实际问题。
二、教学内容1. 随机变量的概念及分类。
2. 随机变量的分布函数及其性质。
3. 离散型随机变量的概率分布：二项分布、泊松分布、超几何分布等。
4. 连续型随机变量的概率密度：正态分布、均匀分布、指数分布等。
5. 随机变量的数学期望及其性质。
三、教学方法1. 采用讲授法，系统地介绍随机变量及其分布的概念、性质和计算方法。
2. 利用案例分析，让学生了解随机变量在实际问题中的应用。
3. 借助数学软件或图形计算器，直观地展示随机变量的分布情况。
4. 开展小组讨论，培养学生合作学习的能力。
四、教学准备1. 教学PPT课件。
2. 教学案例及实际问题。
3. 数学软件或图形计算器。
4. 教材、辅导资料。
五、教学过程1. 导入：通过生活实例引入随机变量的概念，激发学生的学习兴趣。
2. 讲解随机变量的定义、分类及其重要性。
3. 讲解随机变量的分布函数及其性质，引导学生理解分布函数的概念。
4. 讲解离散型随机变量的概率分布，结合实例介绍二项分布、泊松分布、超几何分布等。
5. 讲解连续型随机变量的概率密度，介绍正态分布、均匀分布、指数分布等。
6. 讲解随机变量的数学期望及其性质，引导学生掌握数学期望的计算方法。
7. 案例分析：运用随机变量及其分布解决实际问题，提高学生的应用能力。
8. 课堂练习：布置适量练习题，巩固所学知识。
10. 作业布置：布置课后作业，巩固课堂所学。
六、教学评估1. 课堂提问：通过提问了解学生对随机变量及其分布的理解程度。
2. 课堂练习：检查学生解答练习题的情况，评估学生对知识的掌握程度。
3. 课后作业：布置相关作业，收集学生作业情况，评估学生对知识的运用能力。
