卡尔曼滤波算法(含详细推导)

卡尔曼滤波及其算法实现一、卡尔曼滤波原理1.预测步骤：根据系统的动态模型，以当前时刻的状态估计值为输入，预测下一时刻的状态估计值，同时计算预测误差的协方差矩阵。

2.更新步骤：根据测量模型，将测量值与预测值进行比较，通过加权平均的方式获得更新后的状态估计值，同时计算更新后的状态估计误差的协方差矩阵。

通过不断交替进行预测和更新步骤，卡尔曼滤波可以逐渐优化状态估计值，提供对真实状态的更准确估计。

二、卡尔曼滤波算法实现1.初始化：初始化状态估计值和协方差矩阵。

通常将状态估计值初始化为系统的初始状态，协方差矩阵初始化为一个较大的对角矩阵。

2.预测步骤：通过动态模型预测下一时刻的状态估计值和协方差矩阵。

这可以通过以下几个步骤实现：a.预测状态估计值：使用系统的动态模型和当前时刻的状态估计值，进行状态演化预测。

b.预测误差协方差：使用系统的动态模型和当前时刻的协方差矩阵，计算状态估计误差的协方差矩阵。

c.状态类比噪声：加入过程噪声，以考虑由于系统建模不完备引入的不确定性。

3.更新步骤：根据测量模型，将测量值与预测值进行比较，通过加权平均的方式获得更新后的状态估计值和协方差矩阵。

这可以通过以下几个步骤实现：a.计算卡尔曼增益：使用预测误差协方差矩阵和测量模型的噪声协方差矩阵，计算卡尔曼增益。

卡尔曼增益表示预测误差与测量误差之间的权衡关系。

b.更新状态估计值：使用卡尔曼增益和测量偏差，通过加权平均的方式更新状态估计值。

c.更新误差协方差矩阵：使用卡尔曼增益和测量模型的噪声协方差矩阵，通过加权平均的方式更新预测误差的协方差矩阵。

通过不断交替进行预测和更新步骤，可以得到连续的状态估计值和协方差矩阵，用于对真实状态的估计。

总结：卡尔曼滤波是一种基于概率统计的动态系统估计算法，通过预测和更新步骤，逐渐优化对系统状态的估计。

实际应用中，还可以通过扩展卡尔曼滤波（Extended Kalman Filter）和无迹卡尔曼滤波（Unscented Kalman Filter）等方法来处理非线性系统和非高斯噪声，提高滤波的效果。

卡尔曼滤波器算法卡尔曼滤波器算法是一种常见的数据处理算法，它能够通过对数据进行滤波，去除噪声和干扰，提高数据质量，广泛应用于各个领域。

本文将对卡尔曼滤波器算法进行详细介绍，包括其原理、应用场景以及实现方法。

一、卡尔曼滤波器算法的原理卡尔曼滤波器算法的原理是基于贝叶斯概率理论和线性系统理论的。

其核心思想是通过对系统状态的不断测量和预测，根据预测值和实际值之间的误差来调整状态估计值，从而获得更准确的状态估计结果。

具体来说，卡尔曼滤波器算法可以分为两个步骤：预测和更新。

1. 预测步骤在预测步骤中，通过上一时刻的状态估计值和状态转移矩阵对当前时刻的状态进行预测。

状态转移矩阵是描述系统状态变化的数学模型，可以根据实际情况进行定义。

2. 更新步骤在更新步骤中，通过测量值和状态预测值之间的误差，计算出卡尔曼增益，从而根据卡尔曼增益调整状态估计值。

卡尔曼增益是一个比例系数，它的大小取决于预测误差和测量误差的比例。

二、卡尔曼滤波器算法的应用场景卡尔曼滤波器算法具有广泛的应用场景，下面列举几个常见的应用场景：1. 飞机导航系统在飞机导航系统中，卡尔曼滤波器算法可以通过对飞机的位置、速度和姿态等参数进行滤波，提高导航的准确性和精度。

2. 机器人控制系统在机器人控制系统中，卡尔曼滤波器算法可以通过对机器人的位置、速度、姿态和力量等参数进行滤波，提高机器人的控制精度和稳定性。

3. 多传感器融合系统在多传感器融合系统中，卡尔曼滤波器算法可以通过对多个传感器的数据进行滤波和融合，提高数据质量和精度。

三、卡尔曼滤波器算法的实现方法卡尔曼滤波器算法的实现方法具有一定的复杂性，下面介绍一般的实现步骤：1. 定义状态向量和状态转移矩阵根据实际情况，定义状态向量和状态转移矩阵，描述系统状态的变化规律。

2. 定义测量向量和观测矩阵根据实际情况，定义测量向量和观测矩阵，描述传感器测量数据与状态向量之间的联系。

3. 计算预测值和预测误差协方差矩阵根据状态向量、状态转移矩阵和误差协方差矩阵，计算预测值和预测误差协方差矩阵。

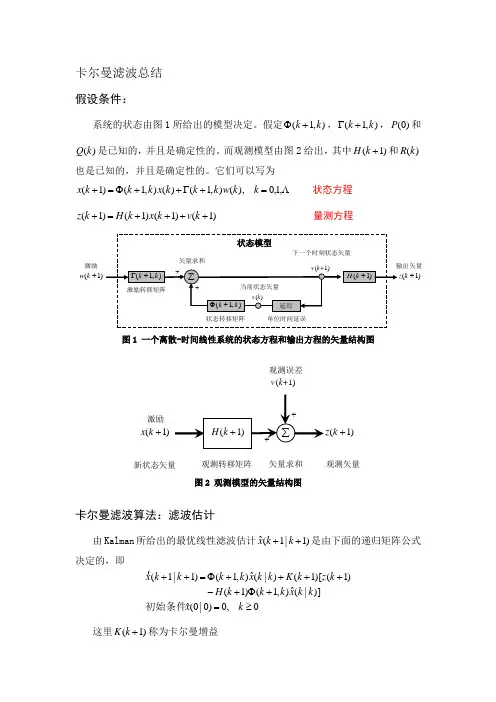
卡尔曼滤波总结假设条件：系统的状态由图1所给出的模型决定。

假定),1(k k+Φ，),1(k k+Γ，)0(P 和)(k Q 是已知的，并且是确定性的。

而观测模型由图2给出，其中)1(+kH 和)(k R 也是已知的，并且是确定性的。

它们可以写为,1,0),(),1()(),1()1(=+Γ++Φ=+k k w k k k x k k k x 状态方程)1()1()1()1(++++=+k v k x k H k z 量测方程)1(+k w激励)1(+k图1 一个离散-时间线性系统的状态方程和输出方程的矢量结构图观测转移矩阵 )1(+k xv (k+1)矢量求和激励)1(+k观测矢量 观测误差新状态矢量图2 观测模型的矢量结构图卡尔曼滤波算法：滤波估计由Kalman 所给出的最优线性滤波估计)1|1(ˆ++k k x是由下面的递归矩阵公式决定的，即,0)0|0(ˆ)]|(ˆ),1()1()1()[1()|(ˆ),1()1|1(≥=+Φ+-++++Φ=++k xk k xk k k H k z k K k k xk k k k x 初始条件这里)1(+kK 称为卡尔曼增益卡尔曼增益卡尔曼增益的表达式为,1,0,)]1()1()|1()1([)1()|1()1(1=+++++⨯++=+-k k R k H k k P k H k H k k P k K TT其中)|1(k kP +表示单步预测误差协方差矩阵。

单步预测误差协方差矩阵（单步性能）1,0)0()0|0(),1()(),1(),1()|(),1()|1(==+Γ+Γ++Φ+Φ=+k P P k k k Q k k k k k k P k k k k P TT，初始条件滤波误差的误差协方差矩阵（协方差递归形式）1,0),|1()]1()1([)1|1(=+++-=+k k k P k H k K I k k P ＋性能评价（系统状态的卡尔曼滤波估计的协方差矩阵）1,0],))1|1(ˆ)1(ˆ))(1|1(ˆ)1([()1|1(=++-+++-+=+k k k x k x k k xk x E k k P T＋11|11|----Γ+Φ=k k k k k k kW XXkkk k V XH Z +=式中：k X —— 是一个1⨯n 维矢量，称为k t 时刻的状态矢量。

卡尔曼滤波详解一维卡尔曼滤波实例解析（五个公式以及各个参数的意义）一、问题描述假设我们有一个一维系统，我们想要估计这个系统的状态x。

我们可以通过一维传感器获得关于这个系统的观测z，但是这个观测会存在误差。

二、基本原理三、基本公式1.状态预测：我们首先假设系统可以通过一个线性方程来描述：x(k)=Ax(k-1)+B(u(k))+w(k)，其中x(k)代表系统在时刻k的真实状态，A是系统的状态转移矩阵，B是外部输入的影响矩阵，u(k)是外部输入，w(k)是系统状态预测过程中的噪声。

2.状态协方差预测：卡尔曼滤波同时也需要估计状态的不确定性，即状态协方差。

协方差可以通过以下公式进行预测：P(k)=AP(k-1)A^T+Q(k-1)，其中P(k)代表状态协方差矩阵，Q(k-1)是协方差预测过程中的噪声。

3.观测预测：将状态的估计值带入观测模型中，可以预测观测值：z^(k)=Hx^(k)，其中z^(k)代表预测的观测值，x^(k)代表状态的估计值，H是观测模型矩阵。

4.观测残差：观测残差即观测值与预测观测值之间的差异：y(k)=z(k)-z^(k)，其中y(k)代表观测残差。

5.状态更新：基于观测残差，我们可以通过以下公式更新状态的估计值：x(k)=x^(k)+K(k)y(k)，其中K(k)代表卡尔曼增益。

卡尔曼增益可以通过以下公式计算：K(k)=P(k)H^T(HP(k)H^T+R)^-1，其中R为观测噪声的方差。

四、参数含义1.状态转移矩阵A：描述系统状态k与状态k-1之间的转移关系。

2.外部输入矩阵B：外部输入对系统状态的影响矩阵。

3.外部输入u(k)：外部输入，可以是控制信号或者测量噪声。

4.状态预测噪声w(k)：在状态预测过程中引入的噪声。

5.状态协方差矩阵P：表示状态估计的不确定性，协方差矩阵的对角线上的元素越大，状态的不确定性越大。

6.状态协方差预测噪声Q(k)：在状态协方差预测过程中引入的噪声。

卡尔曼滤波算法原理及应⽤卡尔曼滤波是⼀种⾼效率的递归滤波器，它能够从⼀系列的不完全及包含噪声的测量中，估计动态系统的状态。

卡尔曼滤波在技术领域有许多的应⽤，常见的有飞机及太空船的导引、导航及控制。

卡尔曼算法主要可以分为两个步骤进⾏：预测和更新。

基于最⼩均⽅误差为最佳估计准则，利⽤上⼀时刻的估计值和状态转移矩阵进⾏预测，⽤测量值对预测值进⾏修正，得到当前时刻的估计值。

卡尔曼算法公式预测：1. ˆs(n |n −1)=A ˆs (n −1|n −1)2. P (n )=A ξ(n −1)A T +Q 更新：3. G (n )=P (n )C T [CP (n )C T +R ]−14. ξ(n )=(I −G (n )C )P (n )5. ˆs(n |n )=ˆs (n |n −1)+G (n )[x (n )−C ˆs (n |n −1)]利⽤上⾯五个式⼦可以递推得到状态的估计值ˆs (n |n )。

⽂章的组织如下：1.基本模型及假设2.卡尔曼算法原理及推导3.卡尔曼滤波算法举例4.Matlab 程序1.基本模型与假设状态⽅程（描述物体运动状态）s (n )=As (n −1)+w (n )测量⽅程（利⽤探测器等器件获取物体状态参数）x (n )=Cs (n )+v (n )其中w (n )为过程噪声，v (n )为测量噪声。

假设：w (n )，v (n )，为独⽴零均值的⽩噪声过程，即E [w (n )w T (k )]=Q (n ),n =k 0,n ≠k E [v (n )v T (k )]=R (n ),n =k 0,n ≠kv (n )和s (n )、w (n )不相关，即E [v (n )s (n )]=0E [v (n )w (n )]=02.卡尔曼算法原理及推导基于最⼩均⽅误差准则，通过观测值x (n )求真实信号s (n )的线性⽆偏最优估计。

已知上⼀时刻的估计值ˆs(n −1|n −1)利⽤状态⽅程对s (n )进⾏预测，最佳预测为{{ˆs(n|n−1)=Aˆs(n−1|n−1)利⽤测量⽅程对x(n)进⾏预测，最佳预测为ˆx(n|n−1)=Cˆs(n|n−1)=CAˆs(n−1|n−1)噪声不参与预测。

第4章 卡尔曼（Kalman ）滤波卡尔曼滤波的思想是把动态系统表示成状态空间形式，是一种连续修正系统的线性投影算法。

功能 1） 连续修正系统的线性投影算法。

2）用于计算高斯ARMA 过程的精确有限样本预测和精确的似然函数。

3） 分解矩阵自协方差生成函数或谱密度。

4）估计系数随时间变化的向量自回归。

第一节 动态系统的状态空间表示一．假设条件令t y 表示时期t 观察到变量的一个()1n ×向量。

则t y 的动态可以用不可观测的()1r ×向量t ξ来表示，t ξ为状态向量。

t y 的动态系统可以表示为如下的状态空间模型：11t t t F v ξξ++=+ （1）t t t t y A x H w ξ′′=++ （2）其中′′F,A ,H 分别为()r r ×，()n k ×和()n r ×矩阵，t x 是外生变量或前定变量的()1k ×向量。

方程（1）称为状态方程，方程（2）称为观察方程。

其中()1r ×向量t v 和()1n ×向量t w 为向量白噪声：()()00t t Qt E v v t R t E w w t ττττττ=⎧′=⎨≠⎩=⎧′=⎨≠⎩ （3）其中,Q R 为()(),r r n n ××矩阵。

假定扰动项t v 和t w 在所有阶滞后都不相关：()0t t E v w ′= 对所有的t 和τ （4）t x 为前定或外生变量，意味着对0,1,2,....,s =除包含在121,,...,t t y y y −−之内的信息外，t x 不再能提供关于t s ξ+以及t s w +的任何信息。

即t x 可能包含y 的滞后值或所有与τ、τξ和w τ不相关变量。

状态空间系统描述有限观察值序列{}1,...,T y y ，需要知道状态向量的初始值1ξ，根据状态方程（1），t ξ可写作()123,,,...,t v v v ξ的线性函数： 2211221....t t t t t t v Fv F v F v F ξξ−−−−=+++++ 2,3,...,t T = （5）这里假定1ξ与t v 和t w 的任何实现都不相关：()()1101,2,...,01,2,...,t t E v TE w Tξτξτ′==′== （6）根据（3）和（6），得t v 和ξ的滞后值不相关：()0t E v τξ′= 1,2,...,1t t τ=−− （7） ()0t E w τξ′= 1,2,...,T τ= （8） ()()()0t t E w y E w A x H w ττττξ′′′=++= 1,2,...,1t t τ=−− （9） ()0t E v y τ′= 1,2,...,1t t τ=−− （10）二．状态空间系统的例子例1 ()AR p 过程，()()()112111...t t t p t p t y y y y µφµφµφµε+−−++−=−+−++−+ （11）()2t t E t τστεετ⎧==⎨≠⎩ （12） 可以写作状态空间形式。

本文将对卡尔曼滤波算法进行示例解析与公式推导，帮助读者更好地理解该算法的原理和应用。

文章将从以下几个方面展开：一、卡尔曼滤波算法的概念卡尔曼滤波算法是一种用于估计动态系统状态的线性无偏最优滤波算法。

它利用系统的动态模型和观测数据，通过迭代更新状态估计值，实现对系统状态的精确估计。

卡尔曼滤波算法最初是由美国工程师鲁道夫·卡尔曼在20世纪60年代提出，随后得到了广泛的应用和研究。

二、卡尔曼滤波算法的原理1. 状态空间模型在卡尔曼滤波算法中，系统的动态模型通常用状态空间模型表示。

状态空间模型由状态方程和观测方程组成，其中状态方程描述系统的演化规律，观测方程描述观测数据与状态之间的关系。

通过状态空间模型，可以对系统的状态进行预测，并与观测数据进行融合，从而估计系统的状态。

2. 卡尔曼滤波的预测与更新卡尔曼滤波算法以预测-更新的方式进行状态估计。

在预测阶段，利用系统的动态模型和之前时刻的状态估计值，对当前时刻的状态进行预测；在更新阶段，将预测值与观测数据进行融合，得到最优的状态估计值。

通过迭代更新，可以不断优化对系统状态的估计，实现对系统状态的精确跟踪。

三、卡尔曼滤波算法的示例解析以下通过一个简单的例子，对卡尔曼滤波算法进行具体的示例解析，帮助读者更好地理解该算法的应用过程。

假设有一个匀速直线运动的物体，其位置由x和y坐标表示，观测到的位置数据带有高斯噪声。

我们希望利用卡尔曼滤波算法对该物体的位置进行估计。

1. 状态空间模型的建立我们建立物体位置的状态空间模型。

假设物体在x和y方向上的位置分别由状态变量x和y表示，动态模型可以用如下状态方程描述：x(k+1) = x(k) + vx(k) * dty(k+1) = y(k) + vy(k) * dt其中，vx和vy分别为x和y方向的速度，dt表示时间间隔。

观测方程可以用如下形式表示：z(k) = H * x(k) + w(k)其中，z(k)为观测到的位置数据，H为观测矩阵，w(k)为观测噪声。

卡尔曼滤波详解卡尔曼滤波是一种常用的状态估计方法，它可以根据系统的动态模型和观测数据，对系统的状态进行估计。

卡尔曼滤波广泛应用于机器人导航、飞行控制、信号处理等领域。

本文将详细介绍卡尔曼滤波的原理、算法及应用。

一、卡尔曼滤波原理卡尔曼滤波的基本思想是利用系统的动态模型和观测数据，对系统的状态进行估计。

在卡尔曼滤波中，系统的状态被表示为一个向量，每个元素表示系统的某个特定状态量。

例如，一个机器人的状态向量可能包括机器人的位置、速度、方向等信息。

卡尔曼滤波的基本假设是系统的动态模型和观测数据都是线性的，而且存在噪声。

系统的动态模型可以表示为：x(t+1) = Ax(t) + Bu(t) + w(t)其中，x(t)表示系统在时刻t的状态向量，A是状态转移矩阵，B是控制矩阵，u(t)表示外部控制输入，w(t)表示系统的过程噪声。

观测数据可以表示为：z(t) = Hx(t) + v(t)其中，z(t)表示系统在时刻t的观测向量，H是观测矩阵，v(t)表示观测噪声。

卡尔曼滤波的目标是根据系统的动态模型和观测数据，估计系统的状态向量x(t)。

为了达到这个目标，卡尔曼滤波将状态估计分为两个阶段：预测和更新。

预测阶段：根据系统的动态模型，预测系统在下一个时刻的状态向量x(t+1)。

预测的过程可以表示为：x^(t+1|t) = Ax^(t|t) + Bu(t)其中，x^(t|t)表示在时刻t的状态向量的估计值，x^(t+1|t)表示在时刻t+1的状态向量的预测值。

卡尔曼滤波还需要对状态的不确定性进行估计，这个不确定性通常用协方差矩阵P(t)表示。

协方差矩阵P(t)表示状态向量估计值和真实值之间的差异程度。

预测阶段中，协方差矩阵也需要进行更新，更新的过程可以表示为：P(t+1|t) = AP(t|t)A' + Q其中，Q表示过程噪声的协方差矩阵。

更新阶段：根据观测数据，更新状态向量的估计值和协方差矩阵。

更新的过程可以表示为：K(t+1) = P(t+1|t)H'(HP(t+1|t)H' + R)^-1x^(t+1|t+1) = x^(t+1|t) + K(t+1)[z(t+1) - Hx^(t+1|t)]P(t+1|t+1) = (I - K(t+1)H)P(t+1|t)其中，K(t+1)表示卡尔曼增益，R表示观测噪声的协方差矩阵，I是单位矩阵。

卡尔曼滤波算法卡尔曼滤波算法卡尔曼滤波器是⼀个“最优化⾃回归数据处理算法”。

对于解决⼤部分的问题，它是最优，效率最⾼甚⾄是最有⽤的。

其⼴泛应⽤已经超过30年，包括机器⼈导航，控制，传感器数据融合甚⾄在军事⽅⾯的雷达系统以及导弹追踪等。

近年来更被应⽤于计算机图像处理，列⼊，⾯部识别，图像分割，图像边缘检测等⽅⾯。

卡尔曼滤波原理⾸先要引⼊⼀个离散控制过程的系统，该系统可⽤⼀个线性随机微分⽅程来秒速：X（k）=AX（k-1）+BU（k）+W（k）（1）再加上系统的测量值：Z（k）=HX（k）+V（k）（2）上两式⼦中，X（k）是k时刻的系统状态，U（k）是k时刻对系统的控制量。

A和B 是系统参数，对于多模型系统，它们为矩阵。

Z（k）是k时刻的测量值，H是测量系统的参数，对于多测量系统，H为矩阵。

W（k）和V(k)分别表⽰过程和测量的噪声。

它们被假设成⾼斯⽩噪声，其协⽅差分别是Q,R,这⾥假设它们不随系统状态变化⽽变化。

由于满⾜上⾯的条件（线性随机微分系统，过程和测量都是⾼斯⽩噪声），卡尔曼滤波器是最优的信息处理器。

下⾯来估算系统的最优化输出。

⾸先利⽤系统的过程模型预测下个状态的系统。

假设现在的系统状态是k，根据系统的模型，可以基于系统的上⼀状态⽽预测出现在状态：X（k|k-1）=AX（k-1|k-1）+BU（k）（3）式（3）中，X（k|k-1）是利⽤上⼀个状态预测的结果，X（k-1|k-1）是上⼀个状态最优的结果，U（k）为现在状态的控制量，如果没有控制量，它可以为0.到现在为⽌，系统结果已经更新了，可是对应于X(k|k-1)的协⽅差还没有更新。

⽤P 表⽰协⽅差：P（k|k-1）=AP（k|k-1）A’+Q（4）式⼦（4）中P（k|k-1）是X（k|k-1）对应的协⽅差，P（k-1|k-1）是X（k-1|k-1）对应的协⽅差，A’表⽰A的转置矩阵，Q时系统过程的协⽅差。

式（3），式（4）就是卡尔曼滤波器5个公式当中的前两个，也就是对系统的预测。

一、背景---卡尔曼滤波的意义随着传感技术、机器人、自动驾驶以及航空航天等技术的不断发展，对控制系统的精度及稳定性的要求也越来越高。

卡尔曼滤波作为一种状态最优估计的方法，其应用也越来越普遍，如在无人机、机器人等领域均得到了广泛应用。

对于Kalman Filter的理解，用过的都知道“黄金五条”公式，且通过“预测”与“更新”两个过程来对系统的状态进行最优估计，但完整的推导过程却不一定能写出来，希望通过此文能对卡尔曼滤波的原理及状态估计算法有更一步的理解。

二、卡尔曼滤波的基本模型假设一离散线性动态系统的模型如下所示：x_{k} = A*x_{k-1} + B*u_{k} + w_{k-1}-------(1)z_{k} = H*x_{k} + v_{k} --------------------(2)其中，各变量表征的意义为：———————————————————————————x_{k}\Rightarrow 系统状态矩阵，-------， z_{k}\Rightarrow 状态阵的观测量（实测）A\Rightarrow 状态转移矩阵，-------， B\Rightarrow 控制输入矩阵H\Rightarrow 状态观测矩阵w_{k-1}\Rightarrow 过程噪声，-------，v_{k}\Rightarrow 测量噪声———————————————————————————如果大家学过《现代控制理论》的话，对上述模型的描述形式一定不会陌生，只是多了变量 w_{k-1} 与 v_{k} 。

其中，随机变量w_{k-1} 代表过程噪声（process noise）， v_{k} 代表测量噪声（measurement noise），且为高斯白噪声，协方差分别为 Q 和 R ，即 p(w) \in N(0,Q) ， p(v) \in N(0,R) 。

为什么要引入这两个变量呢？对于大多数实际的控制系统（如倒立摆系统）而言，它并不是一个严格的线性时变系统(Linear Time System)，亦或系统结构参数的不确定性，导致估计的状态值x_{k} 存在偏差，而这个偏差值由过程噪声 w_{k} 来表征。

卡尔曼滤波算法原理和实现
卡尔曼滤波算法是一种用于估计系统状态的数学方法，它通过融合来自传感器的测量数据和系统模型的预测值，提供对系统状态的最优估计。

该算法最初由R.E. Kalman在1960年提出，被广泛应用于控制系统、导航系统、机器人技术等领域。

该算法的原理可以简要描述为以下几个步骤：
1. 预测（Predict），利用系统的动态模型，根据先验信息和控制输入，预测系统的状态。

2. 更新（Update），根据传感器提供的测量数据，结合预测的状态值和测量的值，计算出最优的状态估计值。

3. 重复，不断地进行预测和更新，以持续地优化对系统状态的估计。

在实现卡尔曼滤波算法时，需要考虑以下几个关键点：
1. 状态方程和观测方程，需要准确地建立描述系统动态特性的
状态方程和观测方程，这两个方程是卡尔曼滤波算法的基础。

2. 状态估计初始化，需要对系统的初始状态进行估计，并设定状态估计的协方差矩阵。

3. 测量数据处理，需要对传感器提供的测量数据进行预处理，确保其符合卡尔曼滤波算法的要求。

4. 参数调节，卡尔曼滤波算法中有一些参数需要根据具体应用进行调节，如过程噪声协方差矩阵和测量噪声协方差矩阵等。

在实际应用中，卡尔曼滤波算法能够有效地处理传感器数据的噪声和不确定性，提供对系统状态的精准估计，因此被广泛应用于导航、目标跟踪、无人车辆等领域。

总的来说，卡尔曼滤波算法通过不断地预测和更新，结合系统模型和测量数据，提供对系统状态的最优估计。

在实现时需要考虑系统模型的准确性、初始状态的估计、测量数据的处理和参数的调节等因素。

希望这个回答能够帮助你更好地理解卡尔曼滤波算法的原理和实现。

卡尔曼滤波算法的程序实现和推导过程---蒋海林（QQ：280586940）---卡尔曼滤波算法由匈牙利裔美国数学家鲁道夫·卡尔曼（Rudolf Emil Kalman）创立，这个数学家特么牛逼，1930年出生，现在还能走能跳，吃啥啥麻麻香，但他的卡尔曼滤波算法已经广泛应用在航空航天，导弹发射，卫星在轨运行等很多高大上的应用中。

让我们一边膜拜一边上菜吧，下面就是卡尔曼滤波算法的经典程序，说是经典，因为能正常运行的程序都长得差不多，在此向原作者致敬。

看得懂的，帮我纠正文中的错误；不太懂的，也不要急，让我慢慢道来。

最后希望广大朋友转载时，能够保留我的联系方式，一则方便后续讨论共同进步，二则支持奉献支持正能量。

void Kalman_Filter(float Gyro,float Accel)///角速度，加速度{///陀螺仪积分角度（先验估计）Angle_Final = Angle_Final + (Gyro - Q_bias) * dt;///先验估计误差协方差的微分Pdot[0] = Q_angle - PP[0][1] - PP[1][0];Pdot[1] = - PP[1][1];Pdot[2] = - PP[1][1];Pdot[3] = Q_gyro;///先验估计误差协方差的积分PP[0][0] += Pdot[0] * dt;PP[0][1] += Pdot[1] * dt;PP[1][0] += Pdot[2] * dt;PP[1][1] += Pdot[3] * dt;///计算角度偏差Angle_err = Accel - Angle_Final;///卡尔曼增益计算PCt_0 = C_0 * PP[0][0];PCt_1 = C_0 * PP[1][0];E = R_angle + C_0 * PCt_0;K_0 = PCt_0 / E;K_1 = PCt_1 / E;///后验估计误差协方差计算t_0 = PCt_0;t_1 = C_0 * PP[0][1];PP[0][0] -= K_0 * t_0;PP[0][1] -= K_0 * t_1;PP[1][0] -= K_1 * t_0;PP[1][1] -= K_1 * t_1;Angle_Final += K_0 * Angle_err; ///后验估计最优角度值Q_bias += K_1 * Angle_err; ///更新最优估计值的偏差Gyro_Final = Gyro - Q_bias; ///更新最优角速度值}我们先把卡尔曼滤波的5个方程贴上来：X(k|k-1)=A X(k-1|k-1)+B U(k) ……… (1)//先验估计 P(k|k-1)=A P(k-1|k-1) A ’+Q ……… (2)//协方差矩阵的预测Kg(k)= P(k|k-1) H ’ / (H P(k|k-1) H ’ + R) ……… (3)//计算卡尔曼增益 X(k|k)= X(k|k-1)+Kg(k) (Z(k) - H X(k|k-1)) ……… (4)通过卡尔曼增益进行修正 P(k|k)=（I-Kg(k) H ）P(k|k-1) ……… (5)//更新协方差阵这5个方程比较抽象，下面我们就来把这5个方程和上面的程序对应起来。