大物例题 一

易错例题详解例1甲、乙两人手拉手玩拔河游戏，结果甲胜乙败，那么甲乙两人谁受拉力大？【错解】因为甲胜乙，所以甲对乙的拉力比乙对甲的拉力大。

就像拔河一样，甲方胜一定是甲方对乙方的拉力大。

【错解原因】产生上述错解原因是学生凭主观想像，而不是按物理规律分析问题。

按照物理规律我们知道物体的运动状态不是由哪一个力决定的而是由合外力决定的。

甲胜乙是因为甲受合外力对甲作用的结果。

甲、乙两人之间的拉力根据牛顿第三定律是相互作用力，甲、乙二人拉力一样大。

【分析解答】甲、乙两人相互之间的拉力是相互作用力，根据牛顿第三定律，大小相等，方向相反，作用在甲、乙两人身上。

【评析】生活中有一些感觉不总是正确的，不能把生活中的经验，感觉当成规律来用，要运用物理规律来解决问题。

例2如图2－1所示，一木块放在水平桌面上，在水平方向上共受三个力，F1，F2和摩擦力，处于静止状态。

其中F1=10N，F2=2N。

若撤去力F1则木块在水平方向受到的合外力为（）免费来自A.10N向左B.6N向右C.2N向左D.0【错解】木块在三个力作用下保持静止。

当撤去F1后，另外两个力的合力与撤去力大小相等，方向相反。

故A正确。

【错解原因】造成上述错解的原因是不加分析生搬硬套运用“物体在几个力作用下处于平衡状态，如果某时刻去掉一个力，则其他几个力的合力大小等于去掉这个力的大小，方向与这个力的方向相反”的结论的结果。

实际上这个规律成立要有一个前提条件，就是去掉其中一个力，而其他力不变。

本题中去掉F1后，由于摩擦力发生变化，所以结论不成立。

【分析解答】由于木块原来处于静止状态，所以所受摩擦力为静摩擦力。

依据牛二定律有F1-F2-f=0此时静摩擦力为8N方向向左。

撤去F1后，木块水平方向受到向左2N的力，有向左的运动趋势，由于F2小于最大静摩擦力，所以所受摩擦力仍为静摩擦力。

此时—F2+f′=0即合力为零。

故D选项正确。

【评析】摩擦力问题主要应用在分析物体运动趋势和相对运动的情况，所谓运动趋势，一般被解释为物体要动还未动这样的状态。

物理大题例题一、选择题（每题3分，共15分）下列关于力的说法正确的是（）A. 物体不受力时，一定保持静止状态B. 物体运动状态改变时，一定受到力的作用C. 作用在物体上的两个力大小相等、方向相反，这两个力一定是平衡力D. 物体受非平衡力作用时，运动状态一定发生改变下列关于声音的说法正确的是（）A. 声音在真空中传播的速度最快B. 一切发声的物体都在振动C. 只要物体振动，我们就能听到声音D. 声音在空气中传播的速度比在水中传播的速度大下列关于光现象的说法正确的是（）A. 漫反射不遵循光的反射定律B. 平面镜可以成实像C. 光从空气斜射入水中时，传播方向一定会发生改变D. 光发生折射时，折射角一定小于入射角二、填空题（每题3分，共15分）牛顿第一定律是在大量经验事实的基础上，通过进一步的________而概括出来的。

演奏小提琴时，是琴弦的________在发声；不断用手指去控制琴弦的长度，这样做的目的是为了改变声音的________。

太阳光经过三棱镜后分解为红、橙、黄、绿、蓝、靛、紫七色光，这种现象叫做光的________。

液体温度计是根据液体________的性质制成的。

冬天，火炉把自己的________能传递给周围空气，此过程是通过________的方式改变物体内能的。

三、解答题（共70分）（10分）一辆汽车以20m/s的速度在平直公路上匀速行驶，突然发现前方有障碍物，立即刹车，汽车以大小是5m/s2的加速度做匀减速直线运动，那么刹车后2s内与刹车后6s内汽车通过的位移之比为多少？（10分）一列长200m的火车以72km/h的速度匀速通过一座长1.8km的大桥，问：（1）火车全部通过大桥需要多长时间？（2）火车全部在桥上的时间是多少？（10分）在探究凸透镜成像规律的实验中，当蜡烛距凸透镜30cm时，在光屏上成一个等大的实像，则凸透镜的焦距是________cm；将蜡烛远离透镜移动到适当位置，要在光屏上成清晰的像，应将光屏向________（远离/靠近）透镜的方向移动。

⼤物实验理论题库⼤物实验理论题库及答案Metaphor1⼀、填空题PART11．依照测量⽅法的不同，可将测量分为和两⼤类。

2．误差产⽣的原因很多，按照误差产⽣的原因和不同性质，可将误差分为疏失误差、和。

3．测量中的视差多属误差；天平不等臂产⽣的误差属于误差。

4．已知某地重⼒加速度值为9.794m/s2，甲、⼄、丙三⼈测量的结果依次分别为：9.790±0.024m/s2、9.811±0.004m/s2、9.795±0.006m/s2，其中精密度最⾼的是，准确度最⾼的是。

5．累加放⼤测量⽅法⽤来测量物理量，使⽤该⽅法的⽬的是减⼩仪器造成的误差从⽽减⼩不确定度。

若仪器的极限误差为0.4，要求测量的不确定度⼩于0.04，则累加倍数N＞。

6．⽰波器的⽰波管主要由、和荧光屏组成。

7．已知y=2X1-3X2+5X3，直接测量量X1，X2，X3的不确定度分别为ΔX1、ΔX2、ΔX3，则间接测量量的不确定度Δy= 。

8、对于0.5级的电压表，使⽤量程为3V，若⽤它单次测量某⼀电压U，测量值为2.763V，则测量结果应表⽰为U= ，相对不确定度为B= 。

9、滑线变阻器的两种⽤法是接成线路或线路。

⼆、判断题（“对”在题号前（）中打√，“错”打×）（10分）（）1、误差是指测量值与真值之差，即误差=测量值－真值，如此定义的误差反映的是测量值偏离真值的⼤⼩和⽅向，既有⼤⼩⼜有正负符号。

（）2、残差（偏差）是指测量值与其算术平均值之差，它与误差定义⼀样。

（）3、精密度是指重复测量所得结果相互接近程度，反映的是随机误差⼤⼩的程度。

（）4、测量不确定度是评价测量质量的⼀个重要指标，是指测量误差可能出现的范围。

（）5、在验证焦⽿定律实验中，量热器中发⽣的过程是近似绝热过程。

（）6、在落球法测量液体粘滞系数实验中，多个⼩钢球⼀起测质量，主要⽬的是减⼩随机误差。

（）7、分光计设计了两个⾓游标是为了消除视差。

第一章 质点运动学一、 基本要求1．掌握位矢、位移、速度、加速度，角速度和角加速度等描述质点运动和运动变化的物理量。

2． 能借助于直角坐标计算质点在平面内运动时的速度、加速度。

3．能计算质点作圆周运动时的角速度和角加速度，切向加速度和法向加速度。

4．理解伽利略坐标，速度变换。

二、 基本内容1．位置矢量（位矢）位置矢量表示质点任意时刻在空间的位置，用从坐标原点向质点所在点所引的一条有向线段r 表示。

r 的端点表示任意时刻质点的空间位置。

r同时表示任意时刻质点离坐标原点的距离及质点位置相对坐标系的方位。

位矢是描述质点运动状态的物理量之一。

注意：（1）瞬时性：质点运动时，其位矢是随时间变化的，即()t r r=；（2）相对性：用r描述质点位置时，对同一质点在同一时刻的位置，在不同坐标系中r 可以是不相同的。

它表示了r的相对性，也反映了运动描述的相对性；（3）矢量性：r为矢量，它有大小，有方向，服从几何加法。

在直角坐标系Oxyz 中k z j y i x r++=222z y x r r ++==r z r y r x ===γβαcos ,cos ,cos质点运动时， ()t r r= （运动方程矢量式）()()()⎪⎩⎪⎨⎧===t z z t y y t x x （运动方程标量式）。

２．位移()(),j y i x t r t t r r ∆+∆=-∆+=∆ r∆的模()()22y x r ∆+∆=∆ 。

注意：（１）r∆与r ∆：前者表示质点位置变化，是矢量，同时反映位置变化的大小和方位；后者是标量，反映质点位置离开坐标原点的距离的变化。

（２）r∆与s ∆：s ∆表示t —t t ∆+时间内质点通过的路程，是标量，只有质点沿直线运动时两者大小相同或0→∆t 时，s r ∆=∆。

3. 速度dtrd v =是描述位置矢量随时间的变化。

在直角坐标系中k v j v i v k dtdz j dt dy i dt dx dt r d v z y x++=++==222222z y x v v v dt dz dt dy dt dx v v ++=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛==v的方向：在直线运动中，v>0表示沿坐标轴正向运动，v <0表示沿坐标轴负向运动。

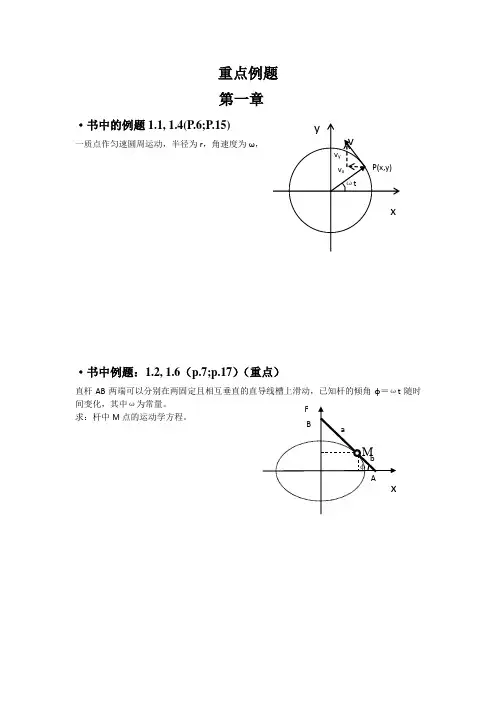
重点例题第一章·书中的例题1.1, 1.4(P.6;P.15)一质点作匀速圆周运动，半径为r，角速度为ω，·书中例题：1.2, 1.6（p.7;p.17）（重点）直杆AB两端可以分别在两固定且相互垂直的直导线槽上滑动，已知杆的倾角φ＝ωt随时间变化，其中ω为常量。

求：杆中M点的运动学方程。

·习题指导P9. 1.4（重点）在湖中有一小船，岸边有人用绳子跨过一高处的滑轮拉船靠岸，当绳子以v 通过滑轮时， 求：船速比v 大还是比v 小？ 若v 不变，船是否作匀速运动？ 如果不是匀速运动,其加速度是多少？·书中例题1.3, 1.5, 1.7（p.7;p.16;p.18）已知：运动学方程：x ＝ －0.31t 2＋7.2t ＋28 y ＝ 0.22t 2－9.1t ＋30 求：t ＝15s 时的位置矢量和方向。

·例题：已知：a ＝100－4t 2，且t ＝0时，v ＝0，x ＝0 求：速度v 和运动学方程x第二章·例题：飞机着陆时受到的阻力为F＝－ct，（c为常数）且t＝0时，v＝v0。

求：飞机着陆时的速度。

·例题：（重点）质量为m的物体以速度v0投入粘性流体中，受到阻力f＝－cv （c为常数）而减速，若物体不受其它力，求：物体的运动速度。

·例题：（重点）光滑的桌面上一质量为M，长为L的匀质链条，有极小一段被推出桌子边缘。

求：链条刚刚离开桌面时的速度。

·例：有一个小球通过一根细线挂在车顶，当车静止时小球铅直向下，当车以加速度a开动时与铅垂线夹角θ。

求：加速度与θ之间的关系。

典型例题·书中例题 2.9（p76 ）（非质点问题的处理方法）试证明在圆柱形容器内，以匀角速度ω绕中心轴作匀速旋转的流体表面为旋转抛物面。

y·书中例题P82，例2.14 (变质量，变力问题)长为L质量为M的均匀柔绳，盘绕在光滑的水平面上，从静止开始，以恒定加速度a竖直向上提绳，当提起的高度为l时，作用在绳端力的大小是多少？当以恒定速度v竖直向上提绳，当提起的高度为l时，作用在绳端力的大小又是多少？第三章·书中例题3.1 (P.95)已知：F＝6x；cosθ＝0.70－0.02x求：质点从x1＝10m到x2＝20m过程中F所作的功。

课时3 物质的量气体摩尔体积一、选择题(本题共7个小题，每题6分，共42分，每个小题只有一个选项符合题意。

)1．三聚氰胺又名蛋白精[分子式：C3N3(NH2)3，相对分子质量：126]是一种低毒性化工产品，婴幼儿大量摄入可引起泌尿系统疾患。

有关三聚氰胺的下列说法正确的是()。

A．2.52 g三聚氰胺含氮原子数目为0.12N A B．标准状况下1 mol的三聚氰胺的体积为22.4 L C．三聚氰胺含氮量约为10% D．三聚氰胺的摩尔质量为126解析三聚氰胺为固体，一分子三聚氰胺中含有6个氮原子，含氮量约为66.7%，摩尔质量为126 g·mol－1。

答案 A2．下列有关气体体积的叙述中，正确的是()。

A．在一定的温度和压强下，各种气态物质体积的大小由气体分子的大小决定B．在一定的温度和压强下，各种气态物质体积的大小由物质的量的多少决定C．不同的气体，若体积不同，则它们所含的分子数一定不同D．气体摩尔体积是指1 mol任何气体所占的体积约为22.4 L解析决定物质体积的因素：①微粒数的多少，②微粒本身的大小，③微粒间的距离。

对于气体物质，在一定温度和压强下，其体积的大小主要由分子数的多少来决定，故A不正确，B正确；气体的体积随温度和压强的变化而变化。

体积不同的气体，在不同的条件下，其分子数可能相同，也可能不同，是无法确定的，故C不正确；气体摩尔体积是指1 mol任何气体所占的体积，其大小是不确定的，会随着温度、压强的变化而变化，22.4 L·mol－1是标准状况下的气体摩尔体积，故D不正确。

答案 B3．在下列条件下，两种气体的分子数一定相等的是()。

A．同密度、同压强的N2和C2H4 B．同温度、同体积的O2和N2C．同体积、同密度的C2H4和CO D．同压强、同体积的O2和N2解析根据阿伏加德罗定律及其推论可以判断A、B、D错误。

C项，同体积、同密度的C2H4和CO质量相等，C2H4和CO的相对分子质量都是28，所以，等质量时两者物质的量相等，分子数也相等。

【典型例题】例1. “小小竹排江中游，巍巍青山两岸走”这歌词中“竹排江中游”是以为参照物，“青山两岸走”是以为参照物．解析：在判断物体是否运动时，一般先确定被研究的物体，其次是选定参照物，最后根据研究物体相对参照物的位置是否发生变化来确定．但此题是一个由已知运动情况来判定参照物的问题，已知竹排在“游”，青山在“走”，请你判定是以哪个物体作为参照物，这就要看竹排相对于“谁”的位置在“游”？在发生位置变化？青山相对于“谁”的位置在“走”？在发生位置变化？竹排在江中移动，显然是相对于江岸即地球而言；青山在走，是由于竹排在运动时，竹排上的人感觉到的，是以自己即竹排为参照物的。

注意：①参照物一旦被选定，我们就假定该物体是静止的。

②参照物的选定可以是任意的，但不能将研究的物体本身作参照物，因自己以自己为参照物，任何物体的位置都是永远不变的，也就是这一物体永远处于静止状态。

③为了研究机械运动的方便，物理学中一般选取地面或相对于地面静止的物体作为参照物，且可以不加以说明；若选取其他合适的物体作参照物研究机械运动时，则要做出说明．正确答案：青山或河岸；竹排。

例２. 下列现象中，能够说明物体的分子在不停地做无规则运动的是（）A. 房间几天不打扫就会有一层灰尘B. 水从高处流向低处C. 放在空气中的铁器过段时间生锈了D. 在一杯白开水中放入白糖，这杯水就有甜味了解析：选项A中房间中的灰尘是空气中的尘埃受重力作用落下而形成的，选项B中的水从高处流向低处是由于重力的作用，选项C中铁器生锈是化学变化，以上三种现象均不能说明分子在不停地做无规则运动。

而选项D中白糖在水中的扩散正说明了分子在不停地做无规则的运动，使整个杯子里的水变甜。

正确答案：D考点分析：考查学生一切组成物质的分子都在不停地做无规则运动。

下列判断错误的是（）A. 甲飞机正向地面俯冲B. 乙飞机一定在作上升运动C. 乙飞机可能与甲飞机同向运动D. 乙飞机可能静止不动解析：甲飞机中的人是以甲飞机为参照物（认为甲飞机不动），所以看到大地迎面冲来，实际应该是甲飞机正向地面俯冲。

大一物理相对静止火车例题题目
（最新版）
目录
1.题目背景及要求
2.物理知识回顾：相对静止与运动
3.解题步骤详解
4.结论与思考
正文
一、题目背景及要求
今天我们要讲解一道大一物理的例题，题目是“相对静止火车例题”。

题目描述如下：一列火车在平直轨道上以速度 v 行驶，有一乘客以相对速度 u 从火车尾部走到火车头部，求乘客在火车上的运动时间。

这是一个典型的相对静止问题，涉及到运动学和力学的基础知识。

二、物理知识回顾：相对静止与运动
在解答这道题之前，我们先来回顾一下物理学中的相对静止与运动的概念。

1.相对静止：当两个物体之间的相对速度为零时，我们就说这两个物体是相对静止的。

2.相对运动：当两个物体之间的相对速度不为零时，我们就说这两个物体是相对运动的。

三、解题步骤详解
根据题目描述，我们可以将问题分解为以下几个步骤：
1.确定参考系：以火车为参考系。

2.分析问题：乘客在火车上运动，火车是静止的，乘客相对于火车的
速度为 u，那么乘客从火车尾部走到火车头部的速度就是 u。

3.运用公式：根据速度等于路程除以时间的公式，我们可以得出乘客在火车上的运动时间 t=路程/速度。

4.得出结论：根据公式，我们可以得出乘客在火车上的运动时间为 t=火车长度/u。

四、结论与思考
通过这道题目，我们可以巩固和加深对相对静止与运动的理解，同时也训练了我们运用物理知识解决实际问题的能力。

在解题过程中，我们需要注意选择正确的参考系，分析问题的实质，并灵活运用相关公式。

高一必修一物理经典力学典型例题1.倾角θ=37°的斜面底端与水平传送带平滑接触，传送带BC长L=6 m，始终以v0=6m/s的速度顺时针运动。

一个质量m=1 kg的物块从距斜面底端高度h1=5.4m的A点由静止滑下，物块通过B点时速度的大小不变。

物块与斜面、物块与传送带间动摩擦因数分别为μ1=0.5、μ2=0.2，传送带上表面在距地面一定高度处，g取10m/s2。

(sin37°=0.6，cos37°=0.8）（1）求物块由A点运动到C点的时间；（2）求物块距斜面底端高度满足什么条件时，将物块静止释放均落到地面上的同一点D。

2.如图，倾斜的传送带向下匀加速运转，传送带与其上的物体保持相对静止。

那么关于传送带与物体间静摩擦力的方向，以下判断正确的是A．物体所受摩擦力为零B．物体所受摩擦力方向沿传送带向上C．物体所受摩擦力方向沿传送带向下D．上述三种情况都有可能出现3.（2018·江西师大附中）如图是工厂流水生产线包装线示意图，质量均为m=2.5 kg、长度均为l=0.36 m的产品在光滑水平工作台AB上紧靠在一起排列成直线（不粘连），以v0=0.6 m/s 的速度向水平传送带运动，设当每个产品有一半长度滑上传送带时，该产品即刻受到恒定摩擦力F f=μmg而做匀加速运动，当产品与传送带间没有相对滑动时，相邻产品首尾间距离保持2l（如图）被依次送入自动包装机C进行包装。

观察到前一个产品速度达到传送带速度时，下一个产品刚好有一半滑上传送带而开始做匀加速运动。

取g=10 m/s2。

试求：(1)传送带的运行速度v；(2)产品与传送带间的动摩擦因数μ：(3)满载工作时与空载时相比，传送带驱动电动机增加的功率∆P；(4)为提高工作效率，工作人员把传送带速度调成v'=2.4 m/s，已知产品送入自动包装机前已匀速运动，求第(3)问中的∆P′?第(3)问中在相当长时间内的等效∆P′′?4.如图所示，传送带AB段是水平的，长20 m，传送带上各点相对地面的速度大小是2 m/s，某物块与传送带间的动摩擦因数为0.1。

第一章 质点运动的描述教学目标:1．掌握运动方程、位移、速度、加速度的概念 2. 能熟练运用运动方程求解速度、加速度等运动学量 3. 能通过速度、加速度和初始条件求解运动方程4. 熟练掌握切向与法向加速度的意义及其表示式，并能熟练求解圆周运动问题5. 正确认识运动的独立性及运动的叠加原理 例题:1．已知质点的运动方程为j t i t r )84(62-+=，则该质点的轨道方程为 ，质点在第二秒内的位移矢量为 ，质点在第二秒内的速度矢量为 。

2．一质点沿x 轴作直线运动，它的运动学方程为23356x t t t =++- (SI)，则 (1) 质点在t =0时刻的速度=v __________；(2) 加速度为零时，该质点的速度=v _ __。

3. 在地面上以初速度0v ，抛射角为θ斜向上抛出的物体，经t= 时，位移的竖直分量大小是水平分量的2倍。

（不计空气阻力）4. 一质点沿半径为R 的圆周运动，其路程S 随时间t 的变化规律为22ct bt S -=，则质点运动的切向加速度t a = ，法向加速度n a = 。

5．一质点在xy 平面上运动，其运动方程为x=Acost,y=Bsint,且A ≠B ，则该质点运动轨迹是（ ） A 、椭圆 B 、双曲线 C 、抛物线 D 、圆6. 某质点作直线运动的运动学方程为3356x t t =-+ (SI)，则该质点作（ ） A 、 匀加速直线运动，加速度沿x 轴正方向． B 、匀加速直线运动，加速度沿x 轴负方向． C 、变加速直线运动，加速度沿x 轴正方向．D 、变加速直线运动，加速度沿x 轴负方向．7. 一运动质点在某瞬时位于矢径()y x r ,的端点处, 其速度大小为（ ）A 、t r d dB 、t r d dC 、t r d dD 、 22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x8. 某物体的运动规律为t k t 2d /d v v -=，式中的k 为大于零的常量．当0=t 时，初速为v 0，则速度v 与时间t 的函数关系是（ ）A 、0221v v +=ktB 、 0221v v +-=kt C 、02121v v +=kt D 、 02121v v +-=kt9. 一物体从某一确定高度以0v 的速度水平抛出，已知它落地时的速度为 t v，那么它运动的时间是（ ）A 、g t 0v v -B 、 gt 20v v - C 、()g t 2/1202v v - D 、()gt22/1202v v-10. 质点沿半径为R 的圆周作匀速率运动，每T 秒转一圈．在2T 时间间隔中，其平均速度大小与平均速率大小分别为（ ）A 、2πR /T , 2πR/TB 、 0 , 2πR /TC 、0 , 0D 、2πR /T , 0 11. 下列说法中，哪一个是正确的？（ ）A 、一质点在某时刻的瞬时速度是2 m/s ，说明它在此后1 s 内一定要经过2 m 的路程B 、斜向上抛的物体，在最高点处的速度最小，加速度最大C 、物体作曲线运动时，有可能在某时刻的法向加速度为零D 、物体加速度越大，则速度越大12. 一质点沿x 轴运动的规律是542+-=t t x （SI 制）。

例题一、土方工程1.某建筑物有18个规格相同的独立柱。

室外地坪设计标高为－0.3m，基底设计标高为－2.1m，自垫层上表面四边放坡，边坡坡度1：0.5。

室外地坪以下每个基坑内各部分的尺寸及工程量是：C10混凝土垫层2200×1800×100；每个C25钢筋混凝土基础为1.484m3。

土的最初可松性系数K S=1.14，最终可松性系数K`S=1.05。

试求：（1）土方开挖工程量。

（2）应预留多少回填土(以自然状态土体积计)?（3）如果用斗容量为3 m3的汽车运土，需运多少车？解：2、计算图示方格的挖方与填方工程量，已知方格的边长为30m。

3、某基坑底长80m宽50m，深6m，四面放坡，边坡坡度为1：0.5。

已知土的可松性系数Ks＝1.16，K’s＝1.07，（1）试求土方开挖工程量。

（2）若混凝土基础和地下室占有体积为1800m3，则应预留多少回填土（以自然状态土体积计）？（3）如果用斗容量为3.0的汽车进行余土外运，需运多少车？4、场地方格网如下图示，方格网的边长为20m ，双向泄水坡度ix ＝0.2％，iy ＝0.3%，按挖填平衡原则确定其设计标高。

（提示：设计标高H 0)432(4143210∑∑∑∑+++=H H H H nH 考虑泄水坡度时，y y x x i i l i l H H ±±=0' ）二、钢筋混凝土工程1、完成图示各号钢筋的下料长度计算，列出计算式。

2、预应力混凝土屋架，采用机械张拉后张法施工，孔道长度为23.8m，两端张拉，张拉程序为0 103%σcon 采用螺丝端杆锚具，长度为320mm，端杆外露出构件端部长度为120mm，预应力为冷拉Ⅲ级钢筋，直径为25mm，每根长度为8m。

实测钢筋冷拉率γ为4%，弹性回缩率为δ为0.5%，张拉控制应力σcon ＝0.85f pyk （f pyk ＝500N ／mm 2），计算预应力筋的下料长度和最大张拉力。

大物等压过程例题等压过程的特征是系统的压强保持不变，即P为常量，dP=0．设想气缸连续地与一系列有微小温度差的恒温热源相接触，同时活塞上所加的外力保持不变．那么接触产生什么效果呢？就是将有微小的热量传给气体，使气体温度稍微升高，气体对活塞的压强也随之较外界所施的压强增加一微量，于是稍微推动活塞对外做功．由于体积的膨胀，压强降低，从而保证气体在内、外压强的量值保持不变的情况下进行膨胀．所以这一准静态过程是一个等压过程（isobaric process），如图1所示．图 1：气体的等压过程现在我们来计算气体的体积增加dV 时所做的功dW．根据理想气体状态方程，如果气体的体积从V 增加到V+dV，温度从T 增加到T+dT，那么气体所做的功dW=PdV=mMRdT(1)图 2：等压过程中功的计算根据热力学第一定律，系统吸收的热量为dQP=dE+m/MRdT(2)式中，下角标P表示压强不变．当气体从状态I(P,V1,T1)I(P,V1,T1) 等压地变为状态II(P,V2,T2)II(P,V2,T2) 时，气体对外做功为W=∫V2V1PdV=P(V2−V1)(3)或写成W=∫T2T1mMRdT=m/MR(T2−T1)(4)所以，整个过程中传递的热量为QP=E2−E1+m/MR(T2−T1)(5)气体在等压膨胀过程中，所吸收的热量的一部分用来增加内能，另一部分用于气体对外做功；气体在等压压缩过程中，外界对气体做功，同时内能减小，其和等于放出的热量．我们把1mol 气体在压强不变的条件下，温度改变1K1K 所需要的热量叫做气体的摩尔定压热容（molar heat capacity at constant pressure），用CP,mCP,m 表示，即CP,m=dQPm/MdT(6)根据这个定义可得dQP=m/MCP,mdT(7)又因E2−E1=m/MCV,m(T2−T1)(8)我们得到CP,m=CV,m+R(9)式 9 叫做迈耶（J. R. Meyer）公式．它的意义是，1mol1mol 理想气体温度升高1K1K 时，在等压过程中比在等体过程中要多吸收8.31J8.31J 的热量．这部分热量去哪了呢？当然是转化为对外所做的膨胀功．由此可见，普适气体常量RR 等于1mol1mol 理想气体在等压过程中温度升高1K1K 对外所做的功．因Cv,m=iR/2Cv,m=iR/2，从式 9 可知CP,m=i2R+R=i+22R(10)摩尔定压热容CP,mCP,m 与摩尔定容热容CV,mCV,m 之比，用γγ表示，叫做[摩尔]热容比（ratio of [molar] heat capacity）或绝热指数，于是γ=CP,mCV,m=i+2i(11)根据式 11 不难算出：对于单原子分子气体，γ=5/3≈1.67γ=5/3≈1.67；双原子刚性分子气体γ=1.40γ=1.40；多原子刚性分子气体γ≈1.33γ≈1.33．它们也都只与气体分子的自由度有关，而与气体温度无关．无论是定压热容，还是定容热容，它们的共同特点是体现了使物体温度发生变化的难易程度，热容大的物体同样升高1K，所需要的热量也多，这说明温度不易变化，所以物体的热容是其热惯性的量度．我们来看几个例题加深一下对内容的理解．例1温度计用作测温的温度计，为了能和被测物体迅速达到热平衡，它的热容必须很小．例2氮气加热一气缸中贮有氮气，质量为 1.25kg1.25kg，在标准大气压下缓慢地加热，使温度升高1K1K．试求气体膨胀时所做的功WW、气体内能的增量ΔE 以及气体所吸收的热量QP．（活塞的质量以及它与气缸壁的摩擦均可略去）．因过程是等压的，所以W=m/MRΔT=1.250.028×8.31×1J=371J(12)(12)W=m/MRΔT=1.250.028×8.31×1J=371J而因为氮气的i=5i=5，所以CV,m=i2R=20.8J/(mol⋅K)(13)(13)CV,m=i2R=20.8J/(mol⋅K)于是ΔE=mMCV,mΔT=1.250.028×20.8×1J=929J(14)(14)ΔE=mMCV,mΔT=1.250.028×20.8×1J=929J所以，气体在这一过程中所吸收的热量为QP=E2−E1+W=1300J(15)。

高一必修一物理经典力学典型例题1.倾角θ=37°的斜面底端与水平传送带平滑接触，传送带BC长L=6 m，始终以v0=6m/s的速度顺时针运动。

一个质量m=1 kg的物块从距斜面底端高度h1=5.4m的A点由静止滑下，物块通过B点时速度的大小不变。

物块与斜面、物块与传送带间动摩擦因数分别为μ1=0.5、μ2=0.2，传送带上表面在距地面一定高度处，g取10m/s2。

(sin37°=0.6，cos37°=0.8）（1）求物块由A点运动到C点的时间；（2）求物块距斜面底端高度满足什么条件时，将物块静止释放均落到地面上的同一点D。

2.如图，倾斜的传送带向下匀加速运转，传送带与其上的物体保持相对静止。

那么关于传送带与物体间静摩擦力的方向，以下判断正确的是A．物体所受摩擦力为零B．物体所受摩擦力方向沿传送带向上C．物体所受摩擦力方向沿传送带向下D．上述三种情况都有可能出现3.（2018·江西师大附中）如图是工厂流水生产线包装线示意图，质量均为m=2.5 kg、长度均为l=0.36 m的产品在光滑水平工作台AB上紧靠在一起排列成直线（不粘连），以v0=0.6 m/s 的速度向水平传送带运动，设当每个产品有一半长度滑上传送带时，该产品即刻受到恒定摩擦力F f=μmg而做匀加速运动，当产品与传送带间没有相对滑动时，相邻产品首尾间距离保持2l（如图）被依次送入自动包装机C进行包装。

观察到前一个产品速度达到传送带速度时，下一个产品刚好有一半滑上传送带而开始做匀加速运动。

取g=10 m/s2。

试求：(1)传送带的运行速度v；(2)产品与传送带间的动摩擦因数μ：(3)满载工作时与空载时相比，传送带驱动电动机增加的功率∆P；(4)为提高工作效率，工作人员把传送带速度调成v'=2.4 m/s，已知产品送入自动包装机前已匀速运动，求第(3)问中的∆P′?第(3)问中在相当长时间内的等效∆P′′?4.如图所示，传送带AB段是水平的，长20 m，传送带上各点相对地面的速度大小是2 m/s，某物块与传送带间的动摩擦因数为0.1。

高一必修一物理经典力学典型例题1.倾角θ=37°的斜面底端与水平传送带平滑接触，传送带BC长L=6 m，始终以v0=6m/s的速度顺时针运动。

一个质量m=1 kg的物块从距斜面底端高度h1=5.4m的A点由静止滑下，物块通过B点时速度的大小不变。

物块与斜面、物块与传送带间动摩擦因数分别为μ1=0.5、μ2=0.2，传送带上表面在距地面一定高度处，g取10m/s2。

(sin37°=0.6，cos37°=0.8）（1）求物块由A点运动到C点的时间；（2）求物块距斜面底端高度满足什么条件时，将物块静止释放均落到地面上的同一点D。

2.如图，倾斜的传送带向下匀加速运转，传送带与其上的物体保持相对静止。

那么关于传送带与物体间静摩擦力的方向，以下判断正确的是A．物体所受摩擦力为零B．物体所受摩擦力方向沿传送带向上C．物体所受摩擦力方向沿传送带向下D．上述三种情况都有可能出现3.（2018·江西师大附中）如图是工厂流水生产线包装线示意图，质量均为m=2.5 kg、长度均为l=0.36 m的产品在光滑水平工作台AB上紧靠在一起排列成直线（不粘连），以v0=0.6 m/s 的速度向水平传送带运动，设当每个产品有一半长度滑上传送带时，该产品即刻受到恒定摩擦力F f=μmg而做匀加速运动，当产品与传送带间没有相对滑动时，相邻产品首尾间距离保持2l（如图）被依次送入自动包装机C进行包装。

观察到前一个产品速度达到传送带速度时，下一个产品刚好有一半滑上传送带而开始做匀加速运动。

取g=10 m/s2。

试求：(1)传送带的运行速度v；(2)产品与传送带间的动摩擦因数μ：(3)满载工作时与空载时相比，传送带驱动电动机增加的功率∆P；(4)为提高工作效率，工作人员把传送带速度调成v'=2.4 m/s，已知产品送入自动包装机前已匀速运动，求第(3)问中的∆P′?第(3)问中在相当长时间内的等效∆P′′?4.如图所示，传送带AB段是水平的，长20 m，传送带上各点相对地面的速度大小是2 m/s，某物块与传送带间的动摩擦因数为0.1。

⼤物习题答案第3章连续物体的运动第3章连续物体得运动⼀基本要求1 理解描写刚体定轴转动得物理量,并掌握⾓量与线量得关系。

2 理解⼒矩与转动惯量概念,掌握刚体绕定轴转动得转动定律。

3理解⾓动量概念,掌握质点在平⾯内运动以及刚体绕定轴转动情况下得⾓动量守恒定律。

４理解刚体定轴转动得转动动能概念,能载有刚体绕定轴转动得问题中正确得应⽤机械能守恒定律。

5了解流体得特点,掌握理想流体得概念。

6掌握理想流体得连续性⽅程与伯努利⽅程。

７了解伯努利⽅程得应⽤。

⼆基本概念1连续介质在宏观⼒学得范围内如果能忽视物体内部得不连续性,把物体瞧作质量连续分布得质点系。

2刚体⼤⼩与形状得变化可以忽略得连续介质。

3对定轴得⼒矩：⼒得⼤⼩与点到⼒得作⽤线得垂直距离得(⼒臂)乘积。

或=r×F4转动惯量转动惯量就是描述刚体在转动中惯性⼤⼩得物理量。

对于质点系得转动惯量。

如果物体得质量就是连续分布得，上式可写为。

5 质点得⾓动量质点对固定点O得位⽮为,质点m对原点O得⾓动量为６冲量矩⼒矩与作⽤时间得乘积，记作。

7刚体定轴转动得⾓动量8⼒矩得功9⼒矩得功率10刚体得转动动能11流体处于液态与⽓态得物体得统称。

特点就是物体各部分之间很容易发⽣相对运动,即流动性。

1２理想流体绝对不可压缩与完全没有黏性得流体。

１３定常流动流体流经空间任⼀给定点得速度就是确定得，并且不随时间变化。

在流速较低时定常流动得条件就是能够得到满⾜得。

14流线为了形象地描述流体得运动，在流体中画出⼀系列曲线，使曲线上每⼀点得切线⽅向与流经该点流体质点得速度⽅向相同, 这种曲线称为流线。

15流管在定常流动中,通过流体中得每⼀点都可以画⼀条流线。

由流线围成得管状区域, 就称为流管。

１6流量单位时间内流过某⼀截⾯得流体体积, 称为流体流过该截⾯得体积。

三基本规律１刚体定轴转动⾓量与线量得关系=R = R2转动定律刚体绕定轴转动时,刚体得⾓加速度与所受得合外⼒矩成正⽐,与刚体得转动惯量成反⽐，。

人教版物理必修一例题总结（含答案）一直线运动<1>实际问题1如图为运动场部分跑道示意图，甲乙两同学参加400m决赛，甲跑第2道，乙跑第3道，他们同时冲过重点线。

关于他们在整个比赛中的位移和路程，下列说法正确的是A位移相同路程相同B位移相同路程不同C位移不同路程相同D位移不同路程不同2为了使高速公路交通有序、安全，路旁立了许多交通标志．如图11所示，甲图是限速标志(白底、红圈、黑字)，表示允许行驶的最大速度是110 km/h；乙图是路线指示标志，表示到泉州还有100 km.上述两个数据的物理意义是A．110 km/h是平均速度，100 km是位移B．110 km/h是平均速度，100 km是路程C．110 km/h是瞬时速度，100 km是位移D．110 km/h是瞬时速度，100 km是路程3假期小明外出旅行，汽车行驶在沪宁高速公路上，小明两次看到路牌和手表如图(a)、(b)所示，则小明乘坐汽车行驶的平均速度A一定等于26.7m/sB一定大于26.7m/sC 一定小于26.7m/sD可能等于26.7 m/s<2>微元法1如图所示，在倾斜导轨上固定一光电门，让装有挡光片的小车每次从同一位置由静止开始下滑，实验中分别记录了四种挡光片的宽度及相应的挡光时间，数据见表格。

为了尽可能准确得到挡光片开始挡光时小车的瞬时速度，应选择的测量数据是A第1组B 第2组C第3组D第4组<3>平均速度1甲乙两辆汽车沿平直公路从某地同时驶向同一目标，甲车在前一半时间里以速度v1做匀速直线运动，后一半时间里以速度v2做匀速直线运动；乙车在前一半路程中以速度v1做匀速直线运动，后一半路程中以速度v2做匀速直线运动，则A. 甲车先到达B. 乙车先到达C. 甲，乙同时到达D.不能确定<4>物理学史与方向1 在研究物理问题时，如果物体的大小和形状可以忽略不计，我们可以把物体简化成一个具有质量没有大小的点--质点．物理学中类似这种将实际物体抽象为质点的研究方法是A控制变量的方法B观察实验的方法C建立物理模型的方法D科学探究的方法2在物理学发展的过程中，某位科学家开创了理想实验的科学方法，并用这种方法研究了力和运动的关系，这位科学家是A焦耳B亚里士多德C牛顿D伽利略<5>比值问题1一个初速度为零的匀加速直线运动的物体，它在第一秒末，第二秒末，第三秒末的瞬时速度大小之比为A1:1:1B1:2:3C1^2:2^2:3^2D1:3:52对于自由落体运动，下列说法正确的是A．在1s内、2s内、3s内……的位移之比是1∶3∶5∶……B．在1s末、2s末、3s末的速度之比是1∶3∶5C．在第1s内、第2s内、第3s内的平均速度之比是1∶3∶5D．在相邻两个1s内的位移之差都是9.8m？3一列火车由静止从车站出发作匀加速直线运动。

高一物理力学例题经典例题1 有一小孩掉进河里后抱住了一根圆木随水向下飘流,有三条船A、B、C在正对河岸P点的地方同时与圆木相遇,但三条船上的船员都没有注意到圆木上的小孩.A、B 两船逆水上行,C船顺水下行.相对水的速度,B船是A船的1.2倍,C船是B船的1.2倍. 当三条船离开P点行驶30分钟的时候, 船员们从收音机里听到圆木上有小孩需要救助的消息,三条船都立即调转船头,驶向圆木.在离P点6千米的地方,小孩被船员救起. 试回答三条船到达小孩和圆木的先后次序如何?_____.解：以流水为参照物.小孩和原木是静止的.船A上行时速度和下行时速度大小相等,船B也是这样,船C也是这样.船A、B、C 同时从小孩所处的位置向上游和下游行驶,速度不同,在30 分钟内行驶了不同的路程s1、s2、s3;在接下去的30分钟内, 三条船分别沿反方向行驶路程s1、s2、s3,回到小孩所处的位置.答:三条船同时到达小孩和原木.例题2 一列一字形队伍长120m,匀速前进. 通讯员以恒定的速率由队尾跑到队首,又跑回队尾,在此期间,队伍前进了288m. 求通讯员跑动的速率v是队伍前进的速率u的多少倍.分析:顺利解答本题的关键是, 找出通讯员的运动跟队首或队尾的运动的联系.解:设通讯员从队尾跑到队首所用的时间为t1, 从队首跑到队尾所用的时间为t2,那么u(t1+t2)＝288 (1)在t1时间内,通讯员跑动的路程比队首移动的路程多120m:vt1-ut1＝120 (2)在t2时间内,通讯员跑动的路程加上队尾移动的路程等于120m:vt2+ut2＝120 (3)从(2)式中得出t1的表达式,从(3)式中得出t2的表达式,代入(1)式, 可算出:v＝1.5u例题3 一物体作匀变速直线运动,某时刻速度的大小为4m/s, 1s后速度的大小变为10m/s.在这1s内(A)位移的大小可能小于4m(B)位移的大小可能大于10m(C)加速度的大小可能小于4m/s2(D)加速度的大小可能小于10m/s2 (1996年高考全国卷试题)解:取初速度方向为正方向,则v0＝4m/s,v t＝10m/s或-10m/s.由 s＝v t＝(v0+v t)t/2,得 s＝7m或-3m所以位移的大小为7m或3m.选项(A)正确,(B)错误.由 a＝(v t-v0)/t得 a＝6m/s2或-14m/s2所以加速度的大小为6m/s2或14m/s2,选项(C)错误,(D)正确.总之,本题选(A)(D).例题4 在三楼的阳台上 ,一人伸出阳台的手上拿着一只小球, 小球下面由细绳挂着另一个小球.放手,让两小球自由下落,两小球相继落地的时间差为t.又站在四层楼的阳台上,同样放手让小球自由下落,两小球相继落地的时间差为t',则(A)t＜t' (B)t＝t' (C)t＞t'解:从三楼阳台外自由下落,下面的小球着地时,两球具有的速度为v,从四楼阳台外自由下落,下面的小球着地时, 两球具有的速度为v',显然v＜v'.下面的小球着地后,上面的小球以较小的初速度v和较大的初速度v',继续作加速度为g的匀加速运动, 发生一定的位移(等于绳长),所需的时间显然是不同的:t＞t'.选项(C)正确.例题5 一质点由静止从A点出发,先作匀加速直线运动,加速度大小为a,后做匀减速直线运动,加速度大小为3a,速度为零时到达B 点.A、B间距离为s.求质点运动过程中的最大速度.解:设质点第一阶段做匀加速运动的的时间为t1,末速度为 v, 这就是运动过程中的最大速度;设第二阶段做匀减速运动的时间为t2.那么第一阶段的位移为vt1/2,第二阶段的位移为vt2/2, 两者之和应为全程位移: vt1/2+vt2＝s (1)又根据加速度的定义式,有t1＝v/a (2)t2＝v/(3a) (3)将(2)(3)两式代入(1)式:v2/(2a)+v2/(6a)＝s所以 v＝(3as/2)1/2例题6 两辆完全相同的汽车 ,沿水平直路一前一后匀速行驶, 速度均为v0,若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车时的加速度开始刹车.已知前车在刹车过程中所行驶的路程为s,若要保证两车在上述情况下不相撞,则两车在匀速行驶时保持的距离至少应为(A)s (B)2s (C)3s (D)4s(1992年高考全国卷试题)解:汽车从开始刹车到停下这个期间,平均速度为v0/2.在前车开始刹车到停下这段时间内,后车以速度v0匀速行驶, 行驶的距离应为s的两倍,即为2s.从前车开始刹车到两车都停下,前车的位移为s;后车的位移为 (2s+s)＝3s.设前车刹车前(匀速行驶期间)两车的距离为l,为使两车不相撞,应满足:l+s≥3s所以l≥2s本题选(B)例题7 某人离公共汽车尾部20m,以速度v向汽车匀速跑过去, 与此同时汽车以1m/s2的加速度启动,作匀加速直线运动.试问, 此人的速度v分别为下列数值时,能否追上汽车?如果能, 要用多长时间?如果不能,则他与汽车之间的最小距离是多少?(1)v＝4m/s; (2)v＝6m/s; (3)v＝7m/s.思路:假设人不管是否在某一时刻追上了汽车,一直以速度v朝前跑,得出汽车跟人的距离y随时间t变化的函数式. 然后考察对于正值t,y是否可能取零,如果是的,那么能追上,如果不能,那么不能追上.解:假设人不管是否在某一时刻追上了汽车,一直以速度v朝前跑.在时间t内,人的位移等于vt;汽车的位移等于(1/2)at2＝0.5t2.经过时间t时,汽车尾部跟人之间,距离为y＝20+0.5t2-vt即 y＝20+0.5(t2-2vt+v2)-0.5v2即 y＝0.5(t-v)2+20-0.5v2 (*)上式中,y取正值时,表示汽车尾部在人前方y米,y取负值时,表示汽车的尾部在人后面│y│米(前面已假设人即使追上了汽车,也一直朝前跑).(甲)把v＝4代入(*)式得y＝0.5( t-4)2+12 (1)y恒大于零,y最小值为12.(乙)把v＝6代入(*)式得y＝0.5( t-6)2+2 (2)y恒大于零,y最小值为2.(丙)把v＝7代入(*)式得y＝0.5( t-7)2-4.5 (3)容易得出,当t＝4,10时,y＝0,这表示,如果人一直朝前跑, 那么经过4s时,人与汽车尾部平齐,经过10s时, 人又一次与汽车的尾部平齐.结论:(1)如v＝4m/s,则人追不上汽车, 人跟汽车之间的最小距离为 12m.(2)如v＝6m/s,则人追不上汽车, 人跟汽车之间的最小距离为 2m.(3)如v＝7m/s,则人经过4s追上汽车.例题8 杂技演员表演一手抛接三球的游戏时, 三个球都抛过一次后,每一时刻手中最多只有一个球. 如果每只球上升的最大高度都为1.25m,那么每隔多长时间抛出一个球?g取10m/s2.(A)0.33s (B)0.33s到0.50s(C)0.50s (D)1.0s解:每个球做一次竖直上抛运动的时间是t＝2(2h/g)1/2＝2(2×1.25/10) 1/2＝1.0s球从这一次被抛出到下一次被抛出,完成一个周期性运动, 设周期为T.如果每个球在手中停留的时间趋于零,那么T＝t＝1.0s;如果手中总停留着一个球,一个球停留的时间是t',那么T＝t+t' ，且 t'＝(1/3)T那么 T＝(3/2)t＝1.5s.以上考虑的是两个极端情况.实际上1.0s＜T＜1.5s在T时间内抛出三个球,每隔T/3的时间抛出一个球:0.33s＜T/3＜0.5s ，选项(B)正确.请读者考虑：如果每秒钟抛出三个球,那么应使每个球上升多高?(答案:0.56m到1.25m)例题9 小球A从地面上方H高处自由下落,同时在A的正下方,小球B从地面以初速度v竖直上抛.不计空气阻力.要使A、B 发生下述碰撞，v、H应满足什么条件?(甲)在B上升到最高点时相碰;(乙)在B上升的过程中相碰;(丙)在时间T内在空中相碰;(丁)经过时间T时在空中相碰.解:设经过时间t在地面上方h高处相碰.则从开始运动到相碰, 小球A发生的位移大小为(H-h),小球B发生的位移大小为h,则:( H-h)＝(1/2)gt2h＝vt-(1/2)gt2由以上两式得 t＝H/v (1)时间t应小于B球在空中运动的时间:t＜2v/g (2)由(1)(2)得 2v2＞gH (3)(甲)在最高点相碰：t＝v/g (4)由(1)(4)得 v2＝gH (5)所以v、H应满足(5)式.(乙)时间t应小于B球上升时间:t＜v/g (6)由(1)(6)得 v2＞gH (7)所以v、H应满足(7)式.(丙) t≤T (8)由(1)(8)得H≤vT (9)所以v、H应满足(3)(9)两式.(丁) t＝T (10)由(1)(10)得 H＝vT (11)所以v、H应同时满足(3)(11)两式.讨论: (11)代入(3)：v＞gT/2 (12)问题(丁)又可这样回答:v、H应满足(11)(12)两式.从(11)得出v＝H/T,代入(3)或(12)可得H＞gT2/2 (13)问题(丁)还可这样回答:v、H应满足(11)(13)两式.第三章牛顿运动定律例题1 某人在地面上最多能举起32Kg的重物,那么在以2m/s匀加速下降的电梯中,他最多能举起多少Kg的重物?g取10m/s2.解:此人能施加的向上的举力大小为F＝m1g＝32×10N＝320N在匀加速下降的电梯中,设某人用举力F举起了质量为m2的物体.物体的加速度向下,所以合外力也向下. 对这个物体应用牛顿第二定律:m2g-F＝m2a即 m2＝F/(g-a)把举力大小F＝320N,重力加速度大小g＝10m/s2,物体加速度大小a ＝2m/s2代入上式,得m2＝40Kg他最多能举起40Kg的物体.例题2 一个质量为200g的物体,以初速度v0＝20m/s竖直上抛, 上升的最大高度为16m.没有风,且假设物体所受空气阻力的大小始终不变,求物体落回抛出点时的速度大小.g取10m/s2.解:物体受到的空气阻力跟物体相对空气的运动方向相反. 因此,在没有风的情况下, 物体受到的空气阻力跟物体相对地面的运动方向相反.物体上升时,受到的空气阻力向下;下降时, 受到的空气阻力向上.设空气阻力的大小始终为f.物体减速上升时,加速度向下,合外力也向下;加速下降时, 加速度向下,合外力也向下.由牛顿第二定律,物体减速上升时,加速度的大小为a1＝(mg+f)/m即 a1＝g+f/m (1)加速下降时,加速度的大小为a2＝(mg-f)/m即 a2＝g-f/m (2)由匀变速直线运动公式,上升阶段满足v02＝2a1h (3)其中h＝16m.下降阶段满足v2＝2a2h (4)(1)+(2): a1+a2＝2g (5)(3)+(4): v02+v2＝2(a1+a2)h (6)(5)代入(6)得v02+v2＝4gh (7)代入数据得 v＝(240)1/2m/s＝15.5m/s例题3 木块静止在光滑水平面上,子弹以较大的水平速度 v从木块左面射入,从右面射出,木块获得速度u. 设子弹对木块的作用力与速度无关.如v增大 ,则u(A)增大 (B)减小 (C)不变.思路:首先通过考察子弹相对木块的运动, 判断子弹穿行于木块的时间,与子弹的入射速度v有怎样的关系.解:子弹对木块的作用力向前,木块对子弹的作用力向后,这一对作用力是恒定的,在它们的作用下,子弹向前作匀减速直线运动, 木块向前作初速度为零的匀加速直线运动.子弹相对木块作匀加速运动.在子弹对木块的作用力与速度无关这个前提下,增大v以后,子弹匀减速运动的加速度仍为原来的值,木块作匀加速运动的加速度也仍为原来的值,从而子弹相对木块的加速度仍为原来的值.增大v以后,子弹穿行于木块期间,子弹相对木块运动的位移仍等于木块的长度.子弹相对木块运动的初速度等于v,增大v, 意味着增大子弹相对木块运动的初速度.所以增大v以后,子弹穿行于木块的时间减少.在较少的时间内,木块作初速度为零的匀加速运动, 获得的末速度u就较小.选项(B)正确.例题4 如图3-2所示,斜面的倾角为α.质量分别为m1、m2的两木块A、B,用细绳连接.它们与斜面之间的动摩擦因数μ相同 .现在A上施加一个沿斜面向上的拉力F,使A、B一起向上作匀加速运动.求证细绳上的拉力与μ和α无关.解:设A、B一起运动的加速度为a,对A、B组成的整体应用牛顿第二定律可得:F-(m1+m2)gsinα-μ(m1+m2)gcosα＝(m1+m2)a即 F＝(m1+m2)gsinα+μ(m1+m2)gcosα+(m1+m2)a (1)设细绳上的拉力大小为T,对B应用牛顿第二定律可得:T-m2gsinα-μm2gcosα＝m2a即 T＝m2gsinα+μm2gcosα+m2a (2)(1)式除以(2)式得F/T＝(m1+m2)/m2 (3)由(3)式可见,细绳上的拉力决定于拉力F以及两个木块的质量, 与动摩擦因数μ以及斜面的倾角α无关.例题5 如图3-3所示,自由下落的小球,从它接触到竖直放置的轻弹簧开始,到弹簧被压缩到最短的过程中,(A)合力逐渐变小(B)合力先变小后变大(C)速度逐渐变小(D)速度先变小后变大解:小球刚接触到弹簧时,弹簧处于自然状态,弹簧对小球的作用力为零,小球受到的合力等于它受到的重力.在最初一段时间内,小球以自由落体运动的末速度为初速度,继续向下做加速运动. 小球向下运动一段适当的位移时(弹簧被压缩适当的长度时),小球弹簧对小球的向上的支持力大小正好等于重力,这时小球的合外力为零.由于小球已经具有了一定的速度,所以还要向下运动.弹簧被压缩的长度增加时,支持力也增大,支持力超过重力,合力向上, 所以从合外力为零的时刻以后向下的运动是减速运动.向下的减速运动进行到速度减为零为止.速度减为零时,弹簧被压缩到最短.再以后,小球向上运动,弹簧的长度增加.综上所述,小球从接触到弹簧开始, 到弹簧被压缩到最短的过程中,小球的合外力先是向下,逐渐减小,然后向上,逐渐增大;小球先作加速运动,然后作减速运动.选项(B)正确.例题6 如图3-4所示,在水平拉力F的作用下,物体A向右运动, 同时物体B匀速上升.可以判断(A)物体A的运动是匀速运动(B)绳子对物体A的拉力逐渐减小(C)水平地面对物体A的支持力逐渐增大(D)水平地面对物体A的摩擦力逐渐减小解:物体A的速度u跟物体B的速度v满足:v＝ucosθ在v保持不变的情况下,u随着θ的变化而变化:物体A的运动不是匀速运动.由物体B匀速运动,可知绳子对物体B的拉力保持不变. 绳子对物体A的拉力T的大小总等于绳子对B的拉力,也是不变的.物体A的受力情况如图3-5所示,将 T沿水平方向和竖直方向分解为T x、T y,随着θ的减小,T x逐渐增大,T y逐渐减小.作用于物体A的T y、支持力N、重力G，三者满足：T y+N＝GN随着Ty的减小而增大.根据f＝μN水平地面对物体A的滑动摩擦力f随着N的增大而增大综上所述,选项(C)正确.例题7 一质点自倾角为α的斜面上方P点沿光滑的斜槽PB从静止开始下滑,如图3-6所示,为使质点在最短的时间内从P点到达斜面,则斜槽与竖直方向的夹角β应等于______.解:如图3-6作PC垂直于斜面,垂足为C.则∠CPA＝α,∠CPB＝α- β.应用牛顿第二定律可得,质点从斜面上下滑时,加速度为a＝gcosβ应用匀变速直线运动公式可得PB＝(1/2)at2即 t2＝2PB/a＝2[PC/cos(α-β)]/(gcosβ)即 t2＝2PC/[gcos(α-β)cosβ]当α-β＝β ,即β＝α/2 时 ,t2取最小值,t取最小值,质点在最短的时间内从P点到达斜面.例题8 图3-7中A为电磁铁,C为胶木秤盘,A和C(包括支架)的总质量为M,B为铁片,质量为m,整个装置用轻绳悬挂于O点. 当电磁铁通电,铁片被吸引上升的过程中,轻绳上拉力F的大小为( ).(A)F＝Mg (B)Mg＜F＜(M+m)g(C)F＝(M+m)g (D)F＞(M＋m)g (1992年高考上海卷试题)解:铁片离开秤盘时, 电磁铁对它的向上的拉力一定大于地球对它的重力mg.铁片在上升中,逐渐靠近电磁铁,电磁铁对它向上的吸引力逐渐增加,仍大于mg.根据牛顿牛顿第三定律,铁片对电磁铁向下的吸引力, 电磁铁对铁片的吸引力大小相等,大于mg.A和C组成的系统,受力平衡:绳子施加的拉力,等于系统的重力,与铁片对电磁铁向下的吸引力之和,大于(Mg+mg).选项(D)正确.例题9 把一个质量m＝4Kg的长方体木块,分割成两个三棱柱形木块A和B,角α＝30°,然后再对到一起,放在光滑的水平面上, 如图3-8所示.用大小为8N的水平力F沿图示方向推A, A、B 组成的长方体保持原来的形状,沿力的作用方向平动.(1)求A对B的作用力.(2)求A对B的静摩擦力.解:(1)A和B的加速度a,都是沿F方向.B的加速度是A对B的作用力Q产生的.所以,Q的方向跟F的方向相同,如图3-9所示.对A、B组成的系统应用牛顿第二定律:a＝F/m＝(8/4)m/s2＝2m/s2对B应用牛顿第二定律:Q＝(m/2)a＝2×2N＝4N(2)A对B的作用力Q是A对B的压力N和静摩擦力f的合力( 也可以说,Q可以分解为N和f),如图3-10(俯视图)所示.静摩擦力的大小为f＝Q/2＝2N例题10 如图3-11所示,A和B质量相等均为m,A与B之间的动摩擦因数为μ1,静摩擦因数为μ2,B与地面之间的动摩擦因数为μ3.原来在水平拉力F的作用下,A和B彼此相对静止 ,相对地面匀速运动(图3-11(a).撤消F后,A和B彼此保持相对静止,相对地面匀减速运动(图3-11(b).则A、B相对地面匀减速运动的过程中,A、B 之间的摩擦力的大小为(A)μ1mg (B)μ2mg (C)μ3mg (D)F/2解：B与地面之间的压力支持力大小始终等于A、B两个物体的总重力,因此地面对B的滑动摩擦力的大小始终为f＝μ3(2mg)A、B匀速运动时,受力平衡:F＝fA、B一起以加速度a做减速运动时,对于A、B组成的系统来说,地面对B的滑动摩擦力f就是合外力,等于(2ma);对于A来说,B对A的静摩擦力f1就是合力,等于(ma).于是f1＝f/2综合以上三式得:f1＝μ3mg和 f1＝F/2本题选(C)(D).说明:因为A、B没有相对运动,所以A、B之间的动摩擦因数μ1用不到;因为B对A的静摩擦力不一定是最大静摩擦力,所以A、B 之间的静摩擦因数μ2用不到.例题11 如图3-12所示,质量为mA、mB的两个物体A和B 用跨过光滑滑轮的细绳相连.A沿倾角为θ的斜面向下加速下滑.A、B两物体加速度的大小相同,等于a.楔形物体C的下表面是光滑的.求台阶对C水平方向的作用力的大小.解：如图3-13,将物体A的加速度 a沿水平方向和竖直方向分解, 水平分加速度为ax＝acosθ；物体B的加速度是向上的,没有水平分量；滑轮质心的加速度为零.在水平方向上,对由A、B、C以及滑轮，组成的系统，应用质点组牛顿第二定律,有F＝m A a x.由以上两式得F＝m A acosθ .例题12 如图3-14所示,三个质量相同,形状相同的楔形物体, 放在水平地面上.另有三个质量相同的小物体, 分别从斜面顶端沿斜面下滑.由于小物体跟斜面间的动摩擦因数不同, 第一个小物体匀加速下滑;第二个物体匀速下滑; 第三个小物体以一定的初速度匀减速下滑. 三个楔形物体都保持静止,水平面对它们的支持力分别为N1、N2、N3,则(A)N1＝N2＝N3 (B)N1＜N2＜N3 (C)N1＞N2＞N3解:楔形物体和小物体组成的系统受到的外力是: 水面地面对楔形物体的支持力,地球对楔形物体和小物体的重力, 以及水平地面施加于楔形物体的沿着接触面的静摩擦力.小物体匀加速下滑时,加速度沿斜面向下, 将加速度向水平方向和竖直方向分解时,竖直方向的分加速度是向下的. 根据质点组牛顿第二定律,竖直方向的作用力的合力向下,所以支持力N 1小于两者的重力之和.小物体匀速下滑时,加速度为零.支持力N 2等于两者的重力之和.小物体减速下滑时,加速度沿斜面向上, 将加速度沿水平方向和竖直方向分解时,竖直方向的分加速度向上. 根据质点组牛顿第二定律，竖直方向作用力的合力向上，支持力N 3大于两者的重力之和.本题选(B).例题13 如图3-15,光滑水平面上有一块木板,质量为M＝4Kg, 长为L＝1.4m.木板右端放着一个小滑块,小滑块质量为m＝1Kg, 尺寸远小于L,与木板之间的动摩擦因数为μ＝0.4.原来它们都静止,现在大小为F＝28N的水平力向右拉木板,使滑块从木板左端掉下, 此力作用时间至少为多长?解:根据题意,水平力作用一段时间后,滑块会从左端掉下. 这暗示我们,水平力开始作用期间,木板向右的加速度较大,速度较大, 滑块向右的加速度较小,速度较小.在滑块尚未滑到木板左端时,如水平力停止作用,那么在一段时间内,木板向右的速度仍大于滑块,那么此后经一段时间滑块有可能从左端掉下,那时, 木板向右的速度应大于等于木板向右的速度.由此可知,水平力作用适当的一段时间t1后, 木板向右的速度比滑块向右的速度大,大适当的数值,然后撤去水平力,当两者的速度正好相等时,滑块从木板左端掉下.t 1就是水平力作用的最短时间.向右的水平力F开始作用后,木板除受到这个力外,还受到向左的滑块施加的滑动摩擦力f＝μmg＝4N木板的加速度向右,大小为(F-f)/M＝6m/s2滑块受到向右的滑动摩擦力,加速度向右,大小为f/m＝4m/s2经时间t1时,撤去水平力F.此后滑块的加速度仍向右,大小仍为f/m＝4m/s2.木板在向左的滑动摩擦力作用下,加速度向左,大小为f/M＝1m/s2木板相对于滑块始终向右运动,滑块相对于木板始终向左运动.下面以木板为参照物,考察滑块在木板上的运动(图3-16). 滑块第一阶段作初速度为零的匀加速运动,末速度的大小记为v,第二阶段作匀减速运动,末速度为零.第一阶段,加速度的大小为a1＝6-4＝2m/s第二阶段,加速度的大小为a2＝4+1＝5m/s2根据匀变速直线运动公式,有v＝a1t1即 v＝2t1 (1)v＝a2t2＝5t2即 v＝5t2 (2)L＝(v/2)(t1+t2) 即 2.8＝v(t1+t2) (3)由(1)(2(3)得 t1＝1s使滑块从木板左端掉下,水平力F作用时间至少为1s.例题14 如图3-17所示,A、B两个光滑的梯形木块质量均为m, 紧挨着并排放在光滑水平面上.倾角θ＝60°.欲使A、B在水平推力F 作用下,一起加速运动(两者无相对滑动),F不能超过多少?解:A受力情况如图3-18所示.A、B之间没有相对滑动, 意味着两者的加速度相同,都是沿水平方向,设大小为a.对A应用牛顿第二定律:Ncosθ+P＝ mg (1)F-Nsinθ＝ ma (2)对A、B组成的系统应用牛顿第二定律：F＝(m+m)a (3)又 N＞0 (4)P≥0 (5)a＞0 (6)由(2)(3)两式得2F-2Nsinθ＝ F即 N＝F/(2sinθ) (7)将(7)代入(1)得P＝mg-(Fctgθ)/2 (8)mg-Fcosθ/(2sinθ)≥0F≤2mgtg60°F≤2×31/2mg欲使A、B在水平推力F作用下,一起加速运动(两者无相对滑动), F 不能超过2×31/2mg.例题15 如图3-19所示,楔形物体静止在水平面上,左右斜面都是光滑的,α＞β.跨过定滑轮的细绳,系住两个物块 ,物块保持静止. 将细绳切断后,两个滑块运动,楔形物体仍保持静止,此时(A)地面对楔形物体的支持力大小与原来相同(B)地面对楔形物体的支持力比原来小(C)地面对楔形物体有静摩擦力,向左(D)地面对楔形物体有静摩擦力,向右解:两个物块的加速度都是沿斜面向下,都有竖直向下的分量,对两个物块和楔形物体组成的系统应用牛顿第二定律可知:对面对楔形物体的支持力小于三者的重力,比原来小.选项(B)正确,(A)错误.原来左边滑块处于静止状态,外力之和为零, 所以绳子对左边物块的拉力大小等于m1gsinα.原来右边滑块处于静止状态, 外力之和为零,所以绳子对右边物块的拉力大小等于m2gsinβ.而绳子对左边滑块的拉力 ,大小等于绳子对右边滑块的拉力.所以m1gsinα＝m2gsinβ (1)图3-20中,左边滑块对楔形物体的压力N1＝m1gcosα这个力的水平向右的分量为N1x＝N1sinα即 N1x＝m1gcosαsinα (2)类似地,右边滑块对楔形物体的压力N2的水平向左的分量为N2x＝m2gcosβsinβ (3)由α＞β可知 cosα＜cosβ (4)将(1)乘以(4)得m1gsinαcosα＜m2gsinβcosβ (5)由(2)(3)(5)可知N1x＜N2x (6)楔形物体保持静止,外力之矢量和应为零: 地面对楔形物体的静摩擦力跟N1x、N2x三者之矢量和应为零.所以地面对楔形物体的静摩擦力向右.选项(D)正确,(C)错误.总之,本题选项(B)(D)正确.例题16 如图3-21所示，物体A、B质量分别为m1、m2, 叠放在倾角为α的斜面上, A、B之间的静摩擦因数为μ1, B 与斜面之间的动摩擦因数为μ2.A、B保持相对静止,一起加速下滑.μ1、μ2、α相互之间一定满足:(A)μ1≥μ 2 ,tgα＞μ2(B)μ1≤μ 2 ,tgα＞μ2(C)tgα＞μ1≥μ2(D)tgα＞μ2＝μ1解:由物体A和物体B组成的系统,加速度a沿斜面向下, 根据牛顿第二定律有:(m1+m2)gsinα-μ2(m1+m2)gcosα＝(m1+m2)a即 gsinα-μ2gcosα＝a (1)其中 a＞0 (2)由(1)(2)得μ2＜tgα (3)物体A受到的静摩擦力f沿斜面向上,对物体A应用牛顿第二定律:m1gsinα-f＝m1a (4)将(1)代入(4):m1gsinα-f＝m1gsinα-μ2m1gcosα即 f＝μ2m1gcosα (5)根据静摩擦因数的定义,物体A受到的最大静摩擦力为f max＝μ1m1gcosα (6)根据最大静摩擦力的定义有f≤f max (7)由(5)(6)(7)得μ2m1gcosα≤μ1m1gcosα即μ2≤μ1 (8)(3)(8)两式是μ1、μ2、α相互之间一定满足的关系式.只有选项(A)正确.例题17 如图3-22所示,物块A的质量为m A,物块B的质量为m B.A与小车前表面之间的静摩擦因数为μ,小车上表面是光滑的. 当使用适当的推力使小车以“适当的加速度”向左作加速运动时,A、B都相对小车静止,跟小车一起运动. 小车的“适当的加速度”应在什么范围内?解：绳子对B的拉力跟绳子对A的拉力大小相等,设为T. 小车的适当的加速度,其大小设为a.对物体B应用牛顿第二定律:T＝m B a (1)物体A受力情况如图3-23所示.小车对A的静摩擦力f可以向上,也可以向下,图中表示静摩擦力矢量的字母f可以取正值 ,也可以取负值, 其绝对值不能超过最大静摩擦力:-μN≤f≤μN (2)为以后演算的方便,可把(2)式写为两个不等式：f≤μN (3)-μN≤f (4)对物体A应用牛顿第二定律:N＝m A a (5)f+T＝m A g (6)将(1)代入(6)可得f＝m A g-m B a (7)将(5)(7)代入(3)得m A g-m B a≤μm A a即 m A g≤μm A a+m B a于是a≥m A g/(μm A+m B) (8)将(5)(7)代入(4)得-μm A a≤ m A g-m B a即 m B a -μm A a≤ m A g即 a(m B -μm A)≤ m A g (9)(甲)若 m B -μm A＞0则(9)式可化为a≤m A g/(m B-μm A) (9a)(乙)若 m B -μm A＜0则(9)式可化为a≥m A g/(m B-μm A) (9b)(8)被满足时,(9b)自然满足.(丙)若 (m B -μm A)＝0则(9)式自然满足.结论:(一)在 m B -μm A＞0情况下,a的取值由(8)和(9a)的交集确定,即m A g/(μm A+m B)≤ a≤m A g/(m B-μm A)(二)在 m B -μm A＜0情况下,a的取值由(8)和(9b)的交集确定,即a≥m A g/(μm A+m B)(三)在 m B -μm A＝0情况下,a的取值由(8)确定,即a≥m A g/(μm A+m B)以上(二)(三)两条可以合并.例题18 如图3-24所示,两斜面高都是h,倾角分别为α、β,α＜β.滑块1,与左边斜面之间的动摩擦因数为μ1,从顶端由静止而下滑,经过时间t1滑到底端,滑到底端时速度大小为v1.滑块2,与右边的斜面之间的动摩擦因数为μ2,从顶端由静止而下滑,经过时间t2滑到底端,滑到底端时速度大小为v2.(A)若已知v1＝v2,那么可知t1＞t2(B)若已知μ1＝μ2,那么可知v1＝v2(C)若已知t1＝t2,那么可知μ1＜μ2(D)若已知μ1＜μ2,那么可知t1＝t2解:作一般化考虑:斜面高为h,倾角为x, 滑块与斜面之间的动摩擦因数为μ,从顶端由静止而下滑,经过时间t滑到底端, 滑到底端时速度大小为v.在分析受力情况的基础上,根据牛顿第二定律,不难得出,滑块的加速度为a＝gsinx-μgcosx (1)由匀变速直线运动的公式得h/sinx＝(1/2)vt (2)h/sinx＝(1/2)at2 (3)v2＝2ah/sinx (4)(甲)由(2)可知,在v相同的情况下,倾角x越大,时间t越短.(乙)将(1)代入(4)得v2＝2gh(1-μctgx) (5)由(5)可知,在μ相同的情况下,对于不同的倾角x,速度v不同.选项(B)不对.(丙)由(1)(3)得h/sinx＝(1/2)(gsinx-μgcosx)t2 (6)即 2h/(t2sinx)＝gsinx-μgcosx即 2h/(gt2sinxcosx)＝sinx/cosx-μ即μ＝tgx[1-2h/(gt2sin2x)] (7)由(7)式可知,在t相同的情况下,锐角x越大,动摩擦因数μ越大.选项(C)正确.(丁)由(6)可知,时间t跟倾角x和动摩擦因数μ有关,当 x分别取α和β时,不可能对于满足μ1＜μ2的所有的μ1、μ2,时间 t总相同.选项(D)不对.总之,选项(A)(C)正确.例题19 在光滑的水平面上,放着两块长度相同、质量分别为M1和M2的木板, 在两木板的左端各放一个大小形状质量完全相同的。

大一物理相对静止火车例题题目
（实用版）
目录
1.题目背景介绍
2.物理中的相对静止概念
3.火车例题的解析方法
4.相对静止火车例题的答案
正文
1.题目背景介绍
对于许多学习物理的同学来说，大一物理的相对静止火车例题题目可能是一个棘手的问题。

火车的运动状态和相对静止的概念很容易让人困惑，但是只要掌握了正确的解析方法，就能轻松解决这类问题。

2.物理中的相对静止概念
在物理学中，相对静止是指两个物体之间的相对位置不发生变化。

例如，在火车上的人观察火车外的景物时，如果火车是静止的，那么他会觉得火车外的景物是运动的。

但是如果火车开始运动，那么他会发现火车外的景物相对于火车是静止的。

3.火车例题的解析方法
对于火车例题，一般可以采用相对速度的方法进行解析。

首先要确定参考系，然后根据参考系计算出物体的相对速度，最后根据相对速度计算出物体的实际速度。

例如，如果一个人在火车上以 30km/h 的速度向前运动，而火车以 60km/h 的速度向前运动，那么这个人相对于地面的速度就是 90km/h。

4.相对静止火车例题的答案
假设有一列火车在平直的轨道上行驶，火车的速度是 60km/h，而火车上的一个人以 30km/h 的速度向前运动。

那么，这个人相对于地面的速度是多少？
解答：以地面为参考系，这个人相对于地面的速度是 90km/h。