组合体答案

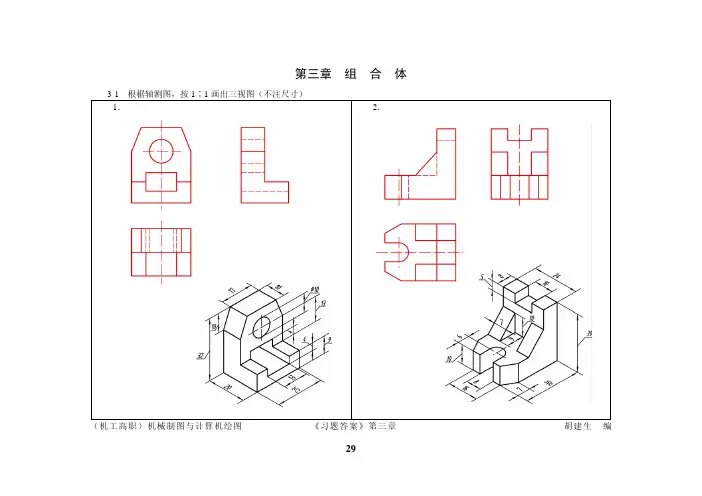
29第三章 组 合 体 3-1 根椐轴测图，按1∶1画出三视图（不注尺寸）1．2．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编30 3-2 参照轴测图，补画视图中所缺的图线（一）1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编31 3-3 参照轴测图，补画视图中所缺的图线（二）1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编3-4 多项选择——选择正确的第三视图，在括号内画√2．3．1．4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编3233 3-5 补画视图中所缺的图线1．2．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编34 3-6 补全俯视图中所缺的图线1．2．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编35 3-7 用简化画法补全相贯线的投影1．2．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编36 3-8 补画第三视图1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编37 3-9 用简化画法补全相贯线的投影1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编38 3-10 检查各视图中尺寸标注是否正确？（将标注错误的尺寸打×）；修改标注不妥的尺寸1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编3-11 补全视图中漏注的尺寸（尺寸数值按1∶1从图中量取整数）1．2．3．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编393-12 先标注立板、三角形肋板和底板的尺寸，再标注组合体的尺寸（按1∶1的比例从图中量取整数）1．2．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编4041 3-13 标注组合体尺寸，尺寸数值按1∶1从图中量取整数（一）1．2．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编42 3-14 标注组合体尺寸，尺寸数值按1∶1从图中量取整数（二）1．2．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编3-16 尺规图作业（画组合体三视图）433-17-1 画组合体三视图443-17-2 画组合体三视图4546 3-18 参照轴测图，补画左视图1．2．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编47 3-19 根据轴测图，补画组合体的另外两个视图（所缺尺寸由轴测图中量取整数）1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编48 3-20 补画俯视图中的漏线1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编49 3-21 已知两视图，补画第三视图（一）1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编50 3-22 已知两视图，补画第三视图（二）1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编51 3-23 补画视图中所缺的图线1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编52 3-24 看懂三视图，补画视图中的漏线或改正画错的图线1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编53 3-25 已知主、俯视图，补画左视图（一）1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编54 3-26 已知主、俯视图，补画左视图（二）1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编55 3-27 已知两视图，补画第三视图1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编56 3-28 根据两面视图，构思物体形状，补画第三视图（有多种答案，至少画出三个）1．2．3． 4．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编57 3-29 根据相同的一面视图，构思不同形状的组合体，补画另外两个视图（未定尺寸自定）1．2．3．4． 5． 6．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编58 3-30 根据已知视图，构思不同形状的组合体，补画所缺的视图（未定尺寸自定）1．2．3．4． 5． 6．（机工高职）机械制图与计算机绘图 《习题答案》第三章 胡建生 编。

大学组合体试题及答案一、单项选择题（每题2分，共20分）1. 组合体的体积等于其各个组成部分体积之和，这是基于什么原理？A. 体积守恒原理B. 体积不变原理C. 体积相加原理D. 体积叠加原理答案：C2. 在组合体中，两个物体的接触面被称为什么？A. 界面B. 接触面C. 表面D. 边界答案：B3. 组合体的表面积计算时，需要考虑哪些因素？A. 各个组成部分的表面积B. 各个组成部分的体积C. 各个组成部分的质量D. 各个组成部分的密度答案：A4. 组合体的重心位置取决于什么？A. 各个组成部分的质量B. 各个组成部分的体积C. 各个组成部分的形状D. 所有上述因素答案：D5. 组合体的稳定性主要受哪些因素影响？A. 重心位置B. 接触面积C. 外部力的作用D. 所有上述因素答案：D二、填空题（每题2分，共20分）1. 当两个物体完全重合时，它们的组合体的体积等于_______。

答案：单个物体的体积2. 组合体的表面积计算时，需要减去_______的面积。

答案：接触面3. 组合体的重心位置可以通过_______的方法来确定。

答案：质量分布4. 如果组合体中的一个物体发生位移，那么组合体的_______也会随之改变。

答案：重心位置5. 组合体的稳定性可以通过增加_______来提高。

答案：接触面积三、简答题（每题10分，共30分）1. 描述组合体的体积计算公式，并举例说明。

答案：组合体的体积计算公式为V = V1 + V2 + ... + Vn，其中V是组合体的总体积，V1、V2、...、Vn是各个组成部分的体积。

例如，如果有一个立方体和一个球体组合在一起，它们的体积分别为V1和V2，那么组合体的体积就是V = V1 + V2。

2. 解释为什么组合体的稳定性与重心位置有关。

答案：组合体的稳定性与重心位置有关，因为重心是物体重力作用的平衡点。

如果重心位置较低，物体就更稳定，因为需要更大的力才能使其倾斜或翻倒。

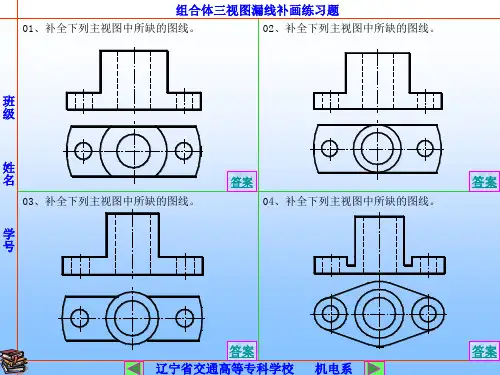
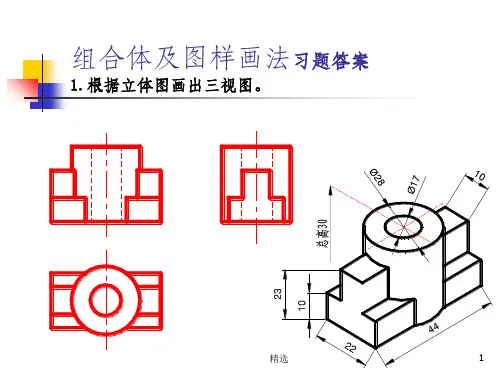
工程制图组合体习题集答案工程制图是一门重要的学科，它是工程设计的基础，也是工程师必备的技能之一。

通过工程制图，可以将设计思想转化为具体的图纸，使得工程师能够清晰地理解和实施设计方案。

为了帮助学习者更好地掌握工程制图，本文将提供一些常见的习题集答案，希望能够对大家的学习有所帮助。

第一题：请根据给定的尺寸和要求，绘制一个简单的平面图。

答案：根据题目要求，我们需要绘制一个简单的平面图。

首先，确定图纸的比例尺，根据尺寸和要求，选择合适的比例尺，例如1:50。

然后，根据给定的尺寸，使用直尺和铅笔在图纸上画出相应的线段和角度。

在绘制过程中，要注意线条的粗细和清晰度，确保图纸的可读性。

最后，根据要求添加文字说明和图例，以使得图纸更加完整和易于理解。

第二题：请根据给定的三视图，绘制一个三维模型。

答案：根据给定的三视图，我们需要将其转化为一个三维模型。

首先，观察三视图，理解各个视图之间的关系和尺寸。

然后，使用透视投影的方法，将三视图上的线段和角度转化为三维空间中的线段和角度。

在绘制过程中，可以使用立体几何的知识，如投影和旋转等，来帮助确定三维模型的形状和位置。

最后，根据需要，可以使用阴影和纹理等技巧，增加模型的逼真度和表现力。

第三题：请根据给定的图纸，计算并绘制出相应的剖面图。

答案：根据给定的图纸，我们需要计算并绘制出相应的剖面图。

首先，观察图纸，理解图纸上的标注和符号。

然后，根据标注和符号，计算出各个构件的尺寸和位置。

在计算过程中，可以使用几何和代数的知识，如相似三角形和平行线等，来帮助确定尺寸和位置的关系。

最后，使用直尺和铅笔在图纸上画出相应的线段和角度，以绘制出剖面图。

通过以上三个习题的解答，我们可以看到工程制图的重要性和复杂性。

在实际工程设计中，工程师需要熟练掌握各种绘图工具和技巧，以便能够准确地表达设计意图。

同时，工程师还需要具备空间想象力和逻辑思维能力，以便能够从平面图到三维模型的转换。

通过不断的练习和学习，相信每个人都能够掌握工程制图的技能，成为一名优秀的工程师。

立体几何中的组合体问题专题(有答案)例1.正方体与球问题:正方体的棱长为1.求球的半径:⑴若正方体的八个顶点都在球面上,⑵若球内切于正方体;⑶12条棱组成一个正方体,一充气球在正方体内,求球的最大半径.例2.正四面体与球问题:正四面体的棱长为1.求球的半径:⑴若正四面体的四个顶点都在球面上,⑵若球内切于正四面体;⑶6条棱组成一个正四面体,一充气球在正四面体内,求球的最大半径.例3.四球问题:四个球的半径都为1.⑴桌面放两两相切的3个球,这3个球上面放一个球,求这个球的最高点离桌面的距离;⑵求与上述4个球都相切的小球的半径.例4.圆锥、圆柱与球⑴底面半径为1cm高为10cm的圆柱内,可以放几个半径为0.5cm的小球?⑵圆锥底面半径为3,高为4,一个球内切于圆锥,求球的半径;⑶圆锥底面半径为3,高为4,两个半径相同的球两两相切,放在圆锥底面上,且内切于圆锥,求这两个球的半径;⑷圆锥底面半径为3,高为4,三个半径相同的球两两相切,放在圆锥底面上,且内切于圆锥,求这两个球的半径;⑸圆锥底面半径为3,内接于一个半径为4的球,求圆锥的高.例5.圆锥与正四棱柱⑴圆锥底面半径为3,高为4,正四棱柱的高为3,且内接于圆锥,求正四棱柱的底面边长;⑵圆锥底面半径为3,高为4,正四棱柱的高为x,且内接于圆锥,求正四棱柱的体积.练习一、补（补成长方体或正方体）1. 一个四面体的所有棱长都为2，四个顶点在同一球面上，则此球的表面积为A 、3πB 、4πC 、33πD 、6π2. 在正三棱锥ABC S -中，M 、N 分别是棱SC 、BC 的中点，且AM MN ⊥，若侧棱32=SA ，则正三棱锥ABC S -外接球的表面积是（ ） A ．π12 B ．π32 C ．π36 D ．π483. 点P 在直径为6的球面上，过P 作两两互相垂直的三条弦（两端点均在球面上的线段），若其中一条弦长是另一条弦长的2倍，则这三条弦长之和的最大值是 A ．6B ．435C ．2215D ．210554. 一个正方体的体积是8，则这个正方体的内切球的表面积是（ ）A ．8πB ．6πC ．4πD ．π 5. 设正方体的棱长为233，则它的外接球的表面积为（ ）A ．π38B ．2πC ．4πD ．π346. 已知三棱锥S ABC -的三条侧棱两两垂直，且2,4SA SB SC ===，则该三棱锥的外接球的半径为 A ．3 B ．6 C ．36 D ．97. 已知长方体1111ABCD A B C D -的外接球的表面积为16，则该长方体的表面积的最大值为A ．32B ．36C ．48D ．648. 长方体1111ABCD A B C D -的各个顶点都在表面积为16π的球O 的球面上，其中1::2:1:3AB AD AA =，则四棱锥O ABCD -的体积为A .263 B . 63C .23D .3 9.【山东省潍坊一中2013届高三12月月考测试数学文】四棱锥P ABCD 的三视图如右图所示，四棱锥P ABCD 的五个顶点都在一个球面上，E 、F 分别是棱AB 、CD 的中点，直线EF 被球面所截得的线段长为22，则该球表面积为A .12B .24C .36D .4810. (河南省豫东、豫北十所名校2013届高三阶段性测试四)已知四面体ABCD 中，AB =AD =6,AC =4,CD =213，AB 丄平面ACD ,则四面体 ABCD 外接球的表面积为A . π36B . π88C . π92D . π12811. 正方体1111ABCD A B C D -的棱长为6，一个球与正方体的棱长都相切，则这个球的半径是____________.12. 三棱锥A -BCD 中，侧棱AB 、AC 、AD 两两垂直，ΔABC ，ΔACD , ΔADB 的面积分别为,222，则三棱锥A -BCD 的外接球的体积为. ______13. 四面体ABCD 中，共顶点A 的三条棱两两相互垂直，且其长分别为361、、，若四面体的四个顶点同在一个球面上，则这个球的表面积为 。