第八章 紫外吸收光谱分析

紫外吸收光谱分析一、电磁波与分子吸收光谱1.1 电磁波的特性电磁波是一种横波，在真空中以光速传播。

电磁波具有波粒二象性波动性：电磁波是以波动的形式传播，具有衍射、干涉及偏振等现象，因此它具有波动性。

粒子性：电磁波由极小、密集的光量子（光子微粒）组成。

电磁辐射的实质是光子的运动。

电磁波在与物质相互作用时，主要表现为粒子性。

电磁波波粒二象性的明显程度与其波长有关：波长愈短，粒子性愈明显；波长愈长，波动特性愈明显。

1.2 电磁波谱γ射线：具有最高能量的微粒。

仅在核反应、高速粒子加速器、宇宙星体剧烈变化时产生X－射线：具有软、硬之分。

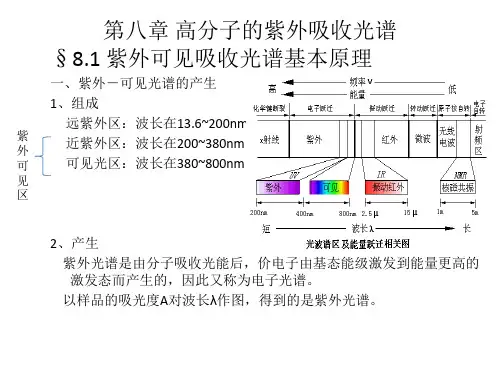
医学上所用的CT、X 透视仪均使用的软X 射线紫外光：包括远紫外（10～200nm）和近紫外（200～400nm）。

远紫外能被空气中的氧吸收（臭氧层）可见光（380 ～780 nm）：复合光与单色光（激光）红外光：分为近红外、红外和远红外三个区域。

微波：能使物质分子“翻转”－微波加热的原理；微波通信等无线电波：射频、视频、短波、中波、长波电磁波波长、频率的关系：λ＝c / υλ－波长（m）；c－光速（3×10 8m·s－1）；υ－频率（Hz）１1.3 电磁波的能量光子作为一种物质微粒具有固有的能量：E＝hυ＝h· c /λE－能量；h－普朗克常数；υ－频率(Hz) ；c－光速；λ－波长(m)电磁波的能量：◆显粒子性时，能量由光子能量的公式而定◆显波动性时，能量主要决定于电磁波振幅1.4 分子的能级与能量有机化合物分子的内部微观运动大致可分为三种，每一种微观运动都有许多种可能的状态，不同的状态具有不同的能量，对应不同的能级。

分子内部的运动与对应的能量如下表所示。

分子内部的运动可分为价电子运动，分子内原子在平衡位置附近的振动和分子绕其重心的转动，这些运动具有相应的能级。

因此分子具有电子能级、振动能级和转动能级。

分子的能量E等于这三种能级的能量之和：E＝Ee＋Ev＋Er分子的各能级之间示意图下图。

紫外吸收光谱解析
紫外吸收光谱解析是一种常见的分析技术，用于研究物质的电子能级结构和分子构成。

该技术基于物质对紫外光的吸收能力，通过测量样品在不同波长下的吸收强度，可以得出分子中的化学键类型、官能团、芳香族与否等信息。

对于药物分析领域来说，紫外吸收光谱解析是一种常用的质量控制方法。

例如，在药品生产过程中，可以通过测量药品在特定波长下的吸收强度来确定药品的纯度和浓度。

同时，在药品质量检验中，可以通过比较药品与标准物质在紫外吸收光谱上的吸收特征，判断药品的合格性。

除了药品分析，紫外吸收光谱解析在环境监测、食品安全、化工等领域也有广泛的应用。

例如，可以通过紫外吸收光谱检测水中污染物的含量，检验食品中添加剂的安全性等。

总之，紫外吸收光谱解析是一种重要的分析技术，对于各个领域的质量控制和检测都有着不可替代的作用。

- 1 -。

第八章紫外吸收光谱分析基本要点：1.理解分子吸收光谱的产生及特征；2. 理解光吸收基本定律和应用于紫外可见分光光度法的条件及其偏离因素；3. 了解紫外-可见分光光度计的主要部件及其类型；4. 理解紫外-可见分光光度法的显色反应条件和测量条件的选择；5. 掌握紫外-可见分光光度法的定性分析和定量分析方法及其应用。

6. 授课时数：3学时∙光学分析法光学分析法—利用辐射与物质间相互作用进行定性、定量的分析方法。

光谱法光学其它光谱：核磁共振、顺磁共振、X射线荧光等分析法非光谱法：折射法、偏振法、旋光法、园二向色散法、X 射线衍射法等∙电磁波一. 电磁波电磁波：实验证实，电磁波（电磁辐射）是一种以极高速度传播的光量子流。

既具有粒子性，也具有波动性。

1. 波动性：其特征是每个光子具有一定的波长，可以用波的参数如波长（ë）、频率（í）、周期（T）、及振幅（A）等来描述。

由于在真空中，所有电磁波均以同样的最大速度―C ‖ 传播，各种辐射在真空中有固定的波长：νλc= (1) 但电磁波在任何介质中的传播速度都比在真空中小，通常用真空中的 ―λ” 值来标记各种不同的电磁波。

波长单位： 紫外可见区 常用 ―nm‖红 外光 区 常用 ―㎛‖微 波 区 常用 ―cm‖2. 粒子性 电磁辐射与物质之间能量的转移用粒子性来解释特征：辐射能是由一颗一颗不连续的粒子流传播的，这种粒子叫光量子，是量子化的（发射或被吸收）。

光量子的能量： E = h ν 式中：h — plank 常数，其值为 6.626⨯10-34 J·S 光量子能量与波长的关系为： λνch h E == （2）例如： λ 为200nm 的光，一个光量子的能量是：由于光量子能量小（10-19J ），因此定义： 1eV （电子伏）= 1.6021⨯10-19 J则 上例中 )(2.6106021.110923.91919eV E =⨯⨯=--由（2）式 可知： λ↑→E ↓， λ ↓ → E ↑即： 随着 λ↑，辐射波动性变得较明显；随着λ↓ ，辐射的粒子性表现的较明显。

紫外吸收光谱分析原理
紫外吸收光谱分析是一种常用的分析方法，用于测定物质在紫外光波段的吸收特性。

其原理基于分子在紫外光波长的辐射下，会吸收特定波长的光能，而波长较短的紫外光可以提供充分的能量，使得分子的电子跃迁至能级更高的激发态。

在紫外吸收光谱分析中，常用的仪器是紫外可见分光光度计。

该仪器通过使用一束连续可见光谱范围的光源，并将光分成几种不同波长的组分。

这束光线经过样品后，会发生吸收作用，被吸收的光能量与样品中存在的物质量成正比。

未被吸收的光线则通过光谱仪，最终转化为一个电子信号。

在分析过程中，将样品和参比物(一般是纯溶剂)分别放入两个
光路，并测量它们的吸收谱线。

通过比较两者的吸收度差异，可以得到样品物质在不同波长下的吸收特性。

这种减法方法可以排除溶剂本身的吸收对结果的影响，提高测量的准确性。

紫外吸收光谱分析在许多领域中都有广泛的应用，特别是在药学、生物化学和环境监测等领域。

通过测定样品的吸收谱线，可以定量测定物质的浓度、检测它们的组分以及判断样品的纯度。

同时，该分析方法快速、灵敏度高，无损伤性，不需要特殊样品处理，是一种非常有效的分析手段。

紫外吸收光谱分析摘要：分子内部的运动可分为价电子运动，分子内原子在平衡位置附近的振动和分子绕其重心的转动。

因此分子具有电子（价电子）能级、振动能级和转动能级。

分子的能量等于三者能量之和。

分子从外界吸收能量之后，就能引起分子能级的跃迁，即从基态能级跃迁到激发态能级。

分子吸收能量具有量子化的特征，即分子只吸收等于两个能级之差的能量。

由于三种能级跃迁所需能量不同，所以需要不同波长的电磁辐射使他们跃迁，即在不同的光学区出现吸收谱带。

由于电子能级跃迁而产生的吸收光谱主要处于紫外及可见光区域（200-780nm），这种分子光谱称为电子光谱或紫外可见光谱。

[1]关键词：电子能级跃迁红移蓝移溶剂效应一、形成原理在有机化合物分子中有形成单键的σ电子、有形成双键的л电子、有未成键的孤对n电子。

当分子吸收一定能量的辐射能时，这些电子就会跃迁到较高的能级，此时电子所占的轨道称为反键轨道，而这种电子跃迁同内部的结构有密切的关系。

在紫外吸收光谱中，电子的跃迁有σ→σ*、n→σ*、π→π*和n→π*四种类型，各种跃迁类型所需要的能量依下列次序减小：σ→σ*>n→σ*>π→π*>n→π*。

一般来说，未成键孤对电子较易激发，成键电子中π电子较相应的σ电子具有较高的能级，而反键电子却相反。

因此简单分子中n→π*跃迁、配位场跃迁需最小的能量，吸收带出现在长波段方向，n→σ*、π→π*及电荷迁移跃迁的吸收带出现在较短波段，而σ→σ*跃迁则出现在远紫外区。

二、紫外吸收光谱与分子结构的关系当饱和单键碳氢化合物中的氢被氧、氮、卤素、硫等杂原子取代时，由于这类原子中有n电子，n电子较σ键电子易于激发，使电子跃迁所需的能量减低，吸收峰向长波方向移动，这种现象称为深色移动或红移，此时产生n→σ*跃迁。

例如甲烷一般跃迁的范围在125~135nm(远紫外区)，碘甲烷（CH3I）的吸收峰则处在150~210（σ→σ*跃迁）及259nm（n→σ*）。