产销平衡的表上作业法
- 格式:doc
- 大小:52.00 KB
- 文档页数:2

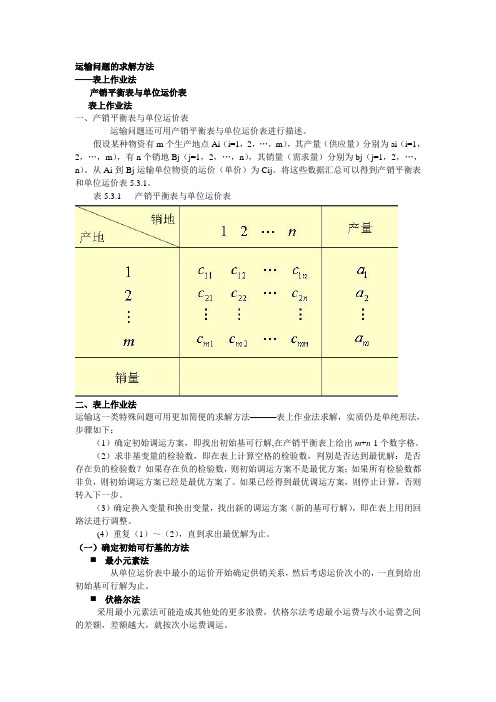
运输问题的求解方法——表上作业法产销平衡表与单位运价表表上作业法一、产销平衡表与单位运价表运输问题还可用产销平衡表与单位运价表进行描述。
假设某种物资有m个生产地点Ai(i=1,2,…,m),其产量(供应量)分别为ai(i=1,2,…,m),有n个销地Bj(j=1,2,…,n),其销量(需求量)分别为bj(j=1,2,…,n)。
从Ai到Bj运输单位物资的运价(单价)为Cij。
将这些数据汇总可以得到产销平衡表和单位运价表5.3.1。
表5.3.1 产销平衡表与单位运价表二、表上作业法运输这一类特殊问题可用更加简便的求解方法———表上作业法求解,实质仍是单纯形法,步骤如下:(1)确定初始调运方案,即找出初始基可行解,在产销平衡表上给出m+n-1个数字格。
(2)求非基变量的检验数,即在表上计算空格的检验数,判别是否达到最优解:是否存在负的检验数?如果存在负的检验数,则初始调运方案不是最优方案;如果所有检验数都非负,则初始调运方案已经是最优方案了。
如果已经得到最优调运方案,则停止计算,否则转入下一步。
(3)确定换入变量和换出变量,找出新的调运方案(新的基可行解),即在表上用闭回路法进行调整。
(4)重复(1)~(2),直到求出最优解为止。
(一)确定初始可行基的方法⏹最小元素法从单位运价表中最小的运价开始确定供销关系,然后考虑运价次小的,一直到给出初始基可行解为止。
⏹伏格尔法采用最小元素法可能造成其他处的更多浪费,伏格尔法考虑最小运费与次小运费之间的差额,差额越大,就按次小运费调运。
(二)最优解的判别计算非基变量(空格)的检验数,当所有的检验数时,为最优解。
求空格检验数的方法有:⏹闭回路法以某一空格为起点找一条闭回路,用水平或垂直线向前划,每碰到一数字格转900后,继续前进,直到回到起始空格为止。
闭回路如图5.3.1的(a)、(b)、(c)等所示。
从每一个空格出发一定存在并且可以找到唯一的闭回路。
因为,m+n-1个数字格(基变量)对应的系数向量是一个基,任一空格(非基变量)对应的系数向量是这个基的线性组合。

§ 3 产销不平衡的运输问题前面讨论的运输问题的理论和方法,都是以产销平衡,即为前提的。
但是在实际问题中产销往往是不平衡的。
对于产销不平衡的运输问题,可以把它们先转化成产销平衡问题,然后再用表上作业法求解。
1.产大于销的情况,即由于总产量大于总销量,就要考虑多余的物资在哪些产地就地贮存问题。
将各产地的仓库设成一个假想销地,该地总需求量为再令运价表中各地到虚设销地的单位运价Ci,n+1 =0,i=1,2…m,则该问题就转化成一个产销平衡问题,可以用表上作业法求解了。
在最优解中,产地Ai到虚设销地的运量实际上就是产地Ai就地贮存的多余物资数量。
2.供不应求的情况,即与产大于销类似,当销大于产时,可以在产销平衡表中虚设一个产地,该产地的产量为再令虚设产地到各销地的单位运价,则问题可以转化为一个产销平衡的运输问题。
在最优解中,虚设产地到销地的运量实际上就是最后分配方案中销地的缺货量。
在产销不平衡问题中,如果某产地不允许将多余物资就地贮存,或不允许缺货,则要令相应运价(M是相当大正数)例2 设有A1、A2、A3三个产地生产某种物资,其产量分别为5,6,8 吨,B1、B2、B3三个销地需要该物资,销量分别为4,8,6 吨,又已知各产销地之间的单位运价如下表所列,试确定总运费最少的调运方案。
解:产地总产量为19 吨,销地总销量为18 吨,产大于销。
故虚设销地B4,令其销量b4=1 吨,运价则问题变成如下运输问题:(1)用最小元素法得初始方案如下表所示:(2)用位势法计算检验数如下表所示:(3)第一次调整量θ=0,调整后的方案如下表所示:(4)再用位势法计算检验数如下表所示:(5)第二次调整量θ=1,调整后的方案如下表所示:(6)再用位势法计算检验数如下表所示:(7)第三次调整量θ=0,调整后的方案如下表所示:(8)再用位势法计算检验数如下表所示:上表中所有检验数均非负。
所以已是最优解。
最小总运费:5×1+6×2+4×2+3×8+1×0=49。



表上作业法产销不平衡例题表上作业法是一种常见的生产管理方法,用于优化生产线上的工作流程。
然而,在实践中,有时可能会出现产销不平衡的情况,即生产速度超过了销售速度或销售速度超过了生产速度。
这种不平衡可能会导致一系列问题,例如库存积压、资金浪费以及客户满意度下降等。
为了更好地理解产销不平衡,我们来看一个例题。
假设某公司生产某种电子产品,每个月的生产能力为10000台。
然而,由于各种原因,该公司只能以每个月8000台的速度销售产品。
这种情况下,就会出现产销不平衡的问题。
首先,由于生产速度大于销售速度,公司可能会面临库存积压的问题。
如果产品堆积在仓库中无法及时售出,就会占用公司的资金和仓储空间。
这不仅增加了公司的运营成本,还可能导致产品过期损坏或降低产品价值。
其次,产销不平衡还会导致公司的资金浪费。
生产所需的原材料、人力资源和设备投入等都需要大量的资金支持。
但是如果产品无法及时销售,公司的资金就会被绑在未售出的产品中,无法用于其他方面的投资。
这将限制公司的发展和增长。
最重要的是,产销不平衡还可能影响客户满意度。
如果公司无法及时满足客户的需求,客户可能会转向竞争对手或者在产品质量和服务方面提出投诉。
这将对公司的声誉和市场地位造成负面影响。
为了解决产销不平衡的问题,公司可以采取以下措施:1. 市场调研和需求预测:通过深入了解市场需求和趋势,公司可以更准确地预测销售量,并相应调整生产计划。
2. 提高销售渠道和营销策略:通过拓展销售渠道,加强市场推广和品牌宣传,提高产品的知名度和销售量。
3. 优化产能和生产计划:根据销售预测调整生产计划,避免过度生产或者产能不足的情况。
同时,优化生产流程和提高生产效率,以适应市场需求。
4. 采取库存管理措施:通过合理的库存管理,例如采用先进的物流和仓储系统,以及及时清理滞销产品,来减少库存积压和产品过期损坏。
综上所述,产销不平衡是生产管理中常见的问题,但可以通过市场调研、销售策略优化和合理的库存管理等措施来解决。
《运筹学》第三版(清华大学出版社)P79例1,表上作业法,运用西北角法确定初始基可行解。
西北角法是从西北角(左上角)格开始,在格内的右下角标上允许取得的最大数;然后按行(列)标下一格的数;若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去;如此进行下去,直至得到一个基本可行解的方法。
西北角法的例子: P79例1从表1中可知,总的产量=总的销量,故产销是平衡的。
第一步:列出运价表和调运物资平衡表。
运用表上作业法时,首先要列出被调运物资的运价表和供需平衡表(简称平衡表),如表1,2所示。
第二步:编制初始调运方案。
首先在表2的西北角方格(即左上角方格,对应变量x11),尽可能取最大值:x11=min{3,7}=3将数值3填入该方格(见表3)。
由此可见x21,x31必须为0,即第一列其他各方格都不能取非零值,划去第一列。
在剩下的方格中,找出其西北角方格x12,x12=min{6,7-3}=4将4填入它所对应方格,第一行饱和,划去该行。
再找西北角方格x22,x22=min{6-4,4}=2将2填入x22所对应方格,于是第二列饱和,划去该列。
继续寻找西北方格为x23,x23=min{5,4-2}=2将2填入x23所对应方格,第二行饱和,划去该行。
剩下方格的西北角方格为x33,x33=min{5-2,9}=3将3填入x33所对应方格,第三列饱和,划去该列。
最后剩下x34方格,取x34 = 6。
这样我们就找到了m+n-1=3+5-1=7个基变量,它们为:x11 = 3,x12 = 4,x22 = 2,x23 = 2,x33 = 3,x34 = 6。
显然它们用折线连接后不形成闭回路。
这就是西北角法所找初始基可行解,所对应的目标值为:2×200+1×250+3×150+1×150+3×250+3×300+4×200=4000我们找到的初始基可行解可通过各行方格中数值之和是否等于产量,各列方格中数值之和是否等于销量来简单验证。
运输问题的表上作业法
最小元素法确定初始可行解——位势法确定最优解——闭回路调整法
如题:某公司在三个地方有三个分厂,生产同一种产品,其产量分别为300箱、400箱、500箱,需要供应四个地方的销售,这四地的产品需求分别为400箱、250箱、350箱、
解:第一步:确定运输问题的类型,是否产销平衡?因为总产量300+400+500=1200,总销量=400+250+350+200=1200,产销平衡。
第二步:确定初始基本可行解。
有两种方法:最小元素法和西北角法。
要自己确定使用哪种方法。
我在这里选择了最小元素法。
好,不管三七二十一,把表搬下来先,不过数据的位置是有研究的,即是放在框的右上角。
并且在右侧添加一个代表产地总产量一列和在下方添加代表销地总销量的一行。
(注释:老师的课件把运价Cij放在框的左下角,而表示基变量的Xij放在框的右上角,这是和我这个不同的地方,不过考试的时候最好标注一
21*0+17*250+25*50+10*400+20*350+22*150 = 19800.
好了,现在开始就解决左下角的那些数字的来源以及带有下划线的数据的缘由了:第一次至第四次表示的是这一行或者一列被划去的时间顺序。
为了说明方便,原表中运价所构成3*4列的矩阵中每个格用Xij表示。
而每个格所对应的运价用Cij表示,这点能明白吧?
好了,现在开始说明最小元素法确定初始基本可行解的过程:
第一:在所有运价中找出最小的元素来分配运输量,可知是10,而对应的意思是从第二分厂生产的产品往甲地运输的单价是10,可以知道甲地的销量是400,第二分厂的最大产量是400,选择min{400,400} = 400,填在框的左下角。
而对应的产量和销量均要减去400,即要划去,填上新的数值。
因为它对应的销量和产量同时为0,是不能同时划去这一行或一列,而是随便划去一行或一列。
我选择划去第二分厂这一行。
第二:同样的道理,在没有划去的其他元素元素中,找出最小的,即17。
其对应的销量是250,产量是300,取min{250,300} = 250,填在框的左下角。
同样对应的销量和产量
也要减去250,即要划去,填上新的数值。
新的数值为0的对应的行或列划去,因为是乙的销量为零,即这一列划去。
第三:同理知20最小,同时把丙这一列划去。
第四:其他同理。
这样我们就确定了3+4-1=6个基变量X11,X12,X14,X21,X33,X34
第三步:使用位势法判断最优解:
i j
是这样的,我们先给u1任意赋值,我令u1=0,由基变量的检验数λij = Cij - u i - v j = 0可分别求得:
λ11 = C11 – u1– v1 = 0 得v1 = C11 – u1 = 21 – 0 = 21
λ21 = C21 – u2– v1 = 0 得u2 = C21 – v1 = 10 – 21 = -11
λ12 = C12 – u1– v2 = 0 得v2 = C12 – u1 = 17 – 0 = 17
λ14 = C14 – u1– v4 = 0 得v4 = C14 – u1 = 25 – 0 = 25
λ34 = C34 – u3– v4 = 0 得u3 = C34 – v4 = 22 – 25 = -3
λ33 = C33 – u3– v3 = 0 得v3 = C33 – u3 = 20+3 = 23
这样,得到了ui和vj后,就可以求的非基变量的检验数:
λ13 = C13 – u1 – v3 = 23 –0 – 23 = 0
λ22 = C22 – u2 – v2 = 15 –(-11)– 17 = 9
λ23 = C23 – u2 – v3 = 30 –(-11)– 23 = 18
λ24 = C24 – u2 – v4 = 19 –(-11)– 25 = 5
λ31 = C31 – u3 – v1 = 23 –(-3)– 21 = 5
λ32 = C32 – u3 – v2 = 21 –(-3)– 17 = 7
最优解判断定理,对于目标函数求最小值的要求非基变量的检验数都大于等于零。
很明显,这些非基变量的检验数都大于零,也就是说我们找到了最优解。
其运输总成本是:21*0+17*250+25*50+10*400+20*350+22*150 = 19800.
白忙活了一天,原来所求出的结果居然不需要迭代,也就是没有用到闭回路调整法,就是说非基变量的检验数都大于零了。
关于闭回路调整法的运用,下次再续。