当前位置：文档之家 › 动量矩定理

动量矩定理

  • 格式：docx
  • 大小：87.07 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

第十三章动量矩定理_理论力学

第十三章动量矩定理_理论力学

式中
分别为作用于质点上的内力和外力。求 n 个方程的矢量和有
式中
，
于 点的主矩。交换左端求和及求导的次序，有
为作用于系统上的外力系对
令 （13-3）
为质系中各质点的动量对 点之矩的矢量和，或质系动量对于 点的主矩，称为质系对 点的动量矩。由此得
（13-4） 式（13-4）为质系动量矩定理，即：质系对固定点 的动量矩对于时间的一阶导数等于外力 系对同一点的主矩。
设 Q 为体积流量， 为密度， 和 分别为水流进口处和出口处的绝对速度， 和 分别为涡轮外圆和内圆的半径， 为 与涡轮外圆切线的夹角， 为 与涡轮内圆切线的
夹角，则
由动量矩定理 得
为叶片作用于水流上的力矩。若水涡轮共有 个叶片，则水流作用于涡轮的转动力矩为
方向与图示方向相反。 §13-2 刚体绕定轴转动微分方程
解：取两叶片间的水流为研究对象（图 13-4 中的兰色部分）。作用于质系上的的外力有 重力和叶片的约束力，重力平行于 z 轴，对转动轴之矩为零。所以外力主矩为叶片对水流
的约束力对 z 轴之矩 。
计算 时间间隔内动量矩的增量 。设 t 瞬时占据 ABCD 的水流，经过 时间间隔
后，运动至占据
，设流动是稳定的，则
有
式中
得
（13-8）
或
（13-9）
此式称为刚体绕定轴转动的微分方程。
为刚体绕定轴转动的角加速度，所以上式
可写为
（13-10）
1．由于约束力对 z 轴的力矩为零，所以方程中只需考虑主动力的矩。 2．比较刚体绕定轴转动微分方程与刚体平动微分方程，即
与
形式相似，求解问题的方法和步骤也相似。 转动惯量与质量都是刚体惯性的度量，转动惯量在刚体转动时起作用，质量在刚体平动

动量矩定理

动量矩定理

第十一章动量矩定理§11-1 引言建立质点或质点系的动量对于某固定点（或固定轴）的矩的变化与作用在该质点或质点系上的力系对同一点（或轴）的主矩之间的关系。

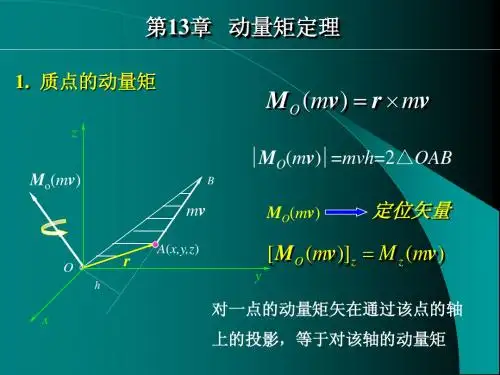
Pr ωε§11-2 动量矩一、质点动量矩Vm r V m M L o o r r r r r ×==)(的动量矩为则质点对固定点的速度为时作空间曲线运动，在瞬的作用下在力的质点设质量为O V t F M m ,r r 方向：右手螺旋法则大小：OAB o S d mV L ∆==2)(1、动量对点之矩V m r L o r r r ×=2、动量对轴之矩)(V m M L z z r =正负：右手规则是标量z L 质点对O 点的动量矩矢在通过O 点的任意轴上的投影，等于质点对该轴的动量矩。

zz O L L =)(r OabS ∆±=2d v m ′′±=)(二、质点系动量矩各质点动量对某点O 的矩的矢量和（即质点系动量对O 点的主矩）称为该质点系对点的动量矩。

n n n o V m r V m r V m r L r r L r r r r r ×++×+×=222111各质点动量对某轴的矩的代数和称为该质点系对该轴的动量矩。

)()()(2211n n z z z z V m M V m M V m M L r L r r +++=∑=)(i i O V m M r r ∑×=i i i V m r r r ∑=)(i i z V m M rV m r L o r r r ×=由§11-3 质点的动量矩定理V m dt r d dt V m d r dt V m r d r r r r r r ×+×=×)()(得：V dt r d r r =∴dt V m r d )(r r ×∴O 点为固定点V m dt r d r r ×∴一、矢量形式0=V m V r r ×=F r r r ×=dt V m d r )(r r ×=oM F)()(F M dt L d F r dt V m r d o o r r r r r r r =×=×或质点的动量对任一固定点的矩对时间的导数等于作用于该质点的力对同一点的矩。

动量矩定理

动量矩定理

mO (F ) mAgr mB gr 0
LO const 0,
即：质点系对轴 O 的动量矩守恒， 且等于零。 vA mAvAar mBvBar 0
O
RO
vB
mAg mBg
见后续
v Aa vBa
即： 二猴的绝对速度永远相等，比赛不分胜负！
二猴爬绳比赛分析 因为二猴的体力有差异，所以
所以得
n d (e) d M M ( m v ) ( 交换求导数与求和的次序 ) ( m ) oi v i ) i i M o ( Fi o dt dt i 1 i 1 i 1 n
n
质点系对定点的动量矩定理
(e) d M o (mi vi ) M o (Fi ) dt i 1 i 1 n n
动量对固定轴z的矩：
[Mo(mv)]z= M z(mv) =±2S△OA'B'
指向：按右手螺旋规则定。
结论：
• 质点的动量对点O的矩称为质点对于O的动量矩。
Mo（mv）= r×mv
矢量
• 质点的动量mv 在Oxy平面内的投影(mv)xy对于点O 的矩定义为质点对于z轴的动量矩。
• 质点对点O的动量矩矢在z轴上的投影，等于质点对z轴的动量矩，即
质点对某轴的动量矩对时间的一 阶导数，等于作用力对于同一轴的矩。
d M ( mv ) M ( F ) x dt x d M ( mv ) M ( F ) y y dt d M ( mv ) M ( F ) z z dt
关于质点动量矩守 恒
• 当MO( F ) = 0 时，有MO( mv ) = 常矢量。
正确解法
Mf
O2 R2

11)动量矩定理

11)动量矩定理

动量矩定理
质点对某定点的动量矩对时间的一阶导数
等于作用力对同一点的矩
第十一章 动量矩定理
2、质点系的动量矩定理
根据质点动量矩定理：
e i d M O mi vi M O Fi M O Fi dt e i d 对于质点系： M O mi vi M O Fi M O Fi dt i 内力总是成对出现： M O Fi 0
时圆盘和人静止，求圆盘的角速度和角加速度
z
v
B
R
O
r

第十一章 动量矩定理

§11-3 刚体绕定轴的转动微分方程
z
F1
O1
定轴转动刚体的动量矩： L J z z
Fn
d 根据动量矩定理： J z M z Fi dt d d 2 Jz J z J z 2 M z F dt dt
第十一章 动量矩定理
将 mi vi mvC 和 vi vC vir 代入： rC mi vi ri mi vi rC mvC ri mi vC vir rC mvC mi ri vC ri mi vir
C
A

e
r
P
第十一章 动量矩定理
3、相对于质心的动量矩定理
dLO d e ri rC ri rC mvC LC ri Fi dt dt e e 右边 rC Fi ri Fi drC dLC d 左边 mvC rC mvC dt dt dt e dLC vC mvC rC maC maC Fi dt e dLC rC Fi dt

7-2动量矩定理

7-2动量矩定理
O
vA
A B
vB
解
取滑轮与A和 两人为研究对象 两人为研究对象， 取滑轮与 和B两人为研究对象， 系统对O点动量矩守恒 点动量矩守恒： 系统对 点动量矩守恒：
r ⋅ (mv A − mvB ) = 0
O
v A = vB
vA
A B
vB
设绳子移动的速率为u 设绳子移动的速率为
v A = u1 − u vB = u2 + u
s w w s LO1 = J O1 ωa + J O1 ωa
s w 记系统总转动惯量为 J O = J O + J O ，有
1 1 1
s w LO1 = J O1 ωa + J O ωrw
ωrw 为动量轮相对卫星的角速度 其中
vA = 0
dLA ( = M Ae ) dt
质系对固定点A的动量矩的变化率等于 质系对固定点 的动量矩的变化率等于 作用在质系上的外力系对A点的主矩 点的主矩。 作用在质系上的外力系对 点的主矩。
( (e (e (e M Ae ) = M Ax) i + M Ay) j + M Az) k
LA = LAx i + LAy j + LAz k dLAy dLAx (e) ( e ) dLAz (e = M Ax , = M Ay , = M Az) Axyz为定系或平动系 为定系或平动系 dt dt dt
LOz = const
当外力系对某固定轴的合力矩等于零时， 当外力系对某固定轴的合力矩等于零时，质系对于 该轴的动量矩保持不变。 该轴的动量矩保持不变。
实例分析
通过改变转动惯量来控制角速度。 通过改变转动惯量来控制角速度。

第11章 动量矩定理

第11章 动量矩定理
指向按右手规则确定； 瞬时量
O点为矩心
M O (F ) r (F )
描述：质点相对某点“转动”运动强度。
§11-1 动量矩计算
质点对轴的动量矩
Lz M z (mv ) [MO (mv )]z
M z (F ) M O (F )
一般规定：
与轴的正向一致（逆时针转动）取“+”， 与轴的正向相反（顺时针转动）取“-”。
n dLx M x (Fi ( e ) ) dt i 1 n dLy M y (Fi ( e ) ) dt i 1
§11-2 动量矩定理
3. 质点动量矩定理(固定点、动点)
A为动点 L A (mv ) r rA mv d d d L A (mv ) r rA mv r rA (mv ) dt dt dt
n (e) dLO MO ( Fi ) dt i 1
其中： LO M O (mi vi ) ri mi vi
i 1 i 1 n n
§11-2 动量矩定理
2. 质点系动量矩定理
B. 对固定轴
n (e) dLz M z ( Fi ) dt i 1
1 4 1 J z r dm r 2rdr 2 R MR2 4 2 0
2 2
R
2 z R 2
要求记住！
§11-1 动量矩计算
D. 匀质薄圆板对于径向轴的转动惯量
圆板对于x与y轴的转动惯量相等： Jx J y
J z mr i m( xi yi ) mx i my i
§11-2 动量矩定理
4. 质点系动量矩定理
任意质点对动点A动量矩定理：

第11章 动量矩定理

第11章 动量矩定理

M z Q(v1r1 cos1 v2r2 cos2 )
例 3 （书上例 11-7，动量矩守恒。）
质量为 m1 = 5kg，半径 r = 30cm 的均质圆盘，可绕铅直轴 z 转
动，在圆盘中心用铰链 D 连接一质量 m2 = 4kg 的均质细杆
AB，AB = 2r，可绕 D 转动。当 AB 杆在铅直位置时，圆盘的
三、 刚体 1. 平动刚体
11-1
LO r MvC
2. 转动刚体（对定轴或平面上定点）
Lz I z
LO IO
3. 平面运动刚体
对质心 C： LC IC
对定点 O： LO mO (MvC ) IC
对瞬心 C＇： LC IC
11.2 动量矩定理
一、 质点动量矩定理
由牛顿第二定律： ma F
l 3g
而 aC
2
4
则
W 3g W
NA W g
4
4
IV. 绳子剪断前后 A 反力的变化：
WW W ΔN A N A N A0
42 4
例 2 例 11-5 （较典型题目）
作业：11-18
11.4 质点系相对动点的动量矩定理(*)
此部分较难，特别是公式推导不易理解。主要掌握两种：①对质心的动量矩定理；②平
m2 g
转速为 n = 90rpm。试求杆转到水平位置，碰到销钉 C 而相对
静止时，圆盘的转速。
解：系统对 z 轴动量矩守恒。
初时系统动量矩： Lz I z盘 1 m1r 2 4
末时系统动量矩： Lz Iz盘 Iz杆 1 m1r2 1 m2 (2r)2
4
12
Lz Lz
11-4
1 4
m1r 2

第十二章 动量矩定理

第十二章 动量矩定理

Lz=Jzω
§2 动量矩定理
一、质点的动量矩定理
设质点质量为m， 受力F， MO(mv) 动量mv，定坐标系Oxyz ， 根据质点的动量定理 z
F
B
mv
r
o A y
MO(F)
d (mv ) F dt
等式两边同时与矢径r作矢量积， 即 x
d (mv ) r F r dt
MO(F)
?
d (mv ) r F 为求等式 r 左边项，先来看 dt d (r mv ) dr mv r d (mv ) dt dt dt v ( r d ( v mv∵O为定点！)mv ) dt MO(mv) =0
第十二章
动量矩定理
z
§1 动量矩的概念
一、质点的动量矩
F r
o
B A m
y
回顾： 力对点的矩 Mo(F)= r×F 若 r=xi+yj+zk F=Fxi+Fyj+Fzk
则 i M o (F ) x Fx
j y Fy k z Fz
MO(F)
x
大小：│Mo(F) │ =2S△OAB
方向：按右手螺旋规则定。
[Mo(mv)]z= M z(mv)
代数量
• 动量矩的量刚为 ML2T－1 （kg· 2/S） m
二、质点系的动量矩
质点系对固定点O的动量矩等于各质点对同 一点O的动量矩的矢量和（即质点系动量对点O 的主矩）：
对定点
Lo M o (mi vi )
i 1
n
矢量
质点系对固定轴z的动量矩等于各质点对同一 轴z的动量矩的代数和，即
vC
C
Lo = M o(Mvc)

理论力学第十一章动量矩定理

理论力学第十一章动量矩定理
当物体作直线运动时，可以用质量作为物体运动惯性的度量； 而当物体绕某轴转动时，转动惯性的大小不仅与质量有关，而 且与半径有关。物体的质量分布距转轴的距离越远，转动惯性 就越大，亦即，越不容易改变转动运动的状态。
2．规则几何形状物体的转动惯量
J Z = ∫ r 2 dm
均质圆环：
J z = ∑ ΔmR 2 =MR 2
往三个坐标轴投影：得到质点对轴的动量矩定理： d m x (mv ) = m x ( F ) dt d m y (mv ) = m y ( F ) dt d m z (mv ) = m z ( F ) dt （1）若Σmo(F)≡0, mo(mv)=常矢量； 两种特殊情况： （2）若Σmx(F)≡0, mx(mv)=常量。 以上两种情况均称为动量矩守恒
R 别为J 1 和J 2 ，两轮的半径分别为 R1 、 2 ，传 动比 i12 = R2 / R1 。轴Ⅰ上作用主动力矩 M 1 ， 轴Ⅱ上有阻力矩 M 2，转向如图。忽略摩擦。 求轴Ⅰ的角加速度。
例 图示传动轴，轴Ⅰ和轴Ⅱ的转动惯量分
Ⅱ
M2
M1
Ⅰ
解 ：分别取轴Ⅰ和Ⅱ为研究对象。受力如图。 两轴对各自轴心的转动微分方程分别为
体积
2π R
π R2
4 π R3 3
4π R 2
Δm
1 1 J O = ∑ ΔMR 2 = MR 2 2 2
N维球
均质直杆：
J z = ∫ x 2 ρ l dx =
0
l
ρl l 3
3
1 2 J z = Ml 3
z
1 1 2 2 J z = ∑ (Δm)l = Ml 3 3
l
x
z
dx
Δm
x

第12章-动量矩定理

第12章-动量矩定理
它表达为刚体质量 m 与某一长度ρ z 旳平方
旳乘积： J z m z2
细直杆 均质圆环 均质圆板
J z /m 1 / 3 l2 z 0.5774 l
J z /m R2 z R
J z /m 1 / 2 R2 z 0.7071R
z 假如把刚体旳质量全部集中在与 轴相距为ρ z 旳点
上，则此质点对 z 轴旳转动惯量与原刚体相同。
四、平行轴定理
J z J z md 2
定理：刚体对任意轴旳转动惯量，等于刚体对 于经过质心、并与该轴平行旳轴旳转动惯量， 加上刚体旳质量与两轴间距离平方旳乘积。
z
O
z
d
ri
ri
C
O
mi
zi
y( y)
C点为质心；
O z 为质心轴，O z
为与之平行旳任
xi
一轴，距离为 d 。
x d x yi J z mi ri2 mi ( xi2 yi2 )
d dt
(
J
z
)
Jz
Mz
dω dt
(Fi
)M
M z (Fi )
z
(
FN
i
)
Fi
或
Jz
d2
dt2
M z (Fi )
或 J z M z (Fi )
FNi
与 m a Fi 比较
例：已知滑轮半径为 R ，转动惯量为 J ，带动滑轮
旳皮带拉力分别为 F1 和 F2 。求滑轮旳角加速度 。
F2 解：根据定轴转动微分方程
d(ri
mivi ) dt
ri
F (e) i
ri
Fi(i)
(i 1,2,, n)
相加得

理论力学第13章动量矩定理

理论力学第13章动量矩定理

mi
rC x′
C
y′ y
mi vi mvC
LC ri mi vi
x
LO rC mvC LC
LO rC mvC LC
dLO d (e) (rC mvC LC ) r i Fi dt dt
r i rC ri
drC dLC d (e) i Fi ( e ) mvC rC mvC r C Fi r dt dt dt
v R
应用动量矩定理
O

FOx
mg
M
(e)
WR
dLO (e ) M dt
WR 2 a W 2 (JO R ) g
P
v
JO W dv ( R) WR R g dt
W
z
例 题3
z
求：此时系统的角速度 解：取系统为研究对象
M
A
(e ) z
0
A
B
a l
a
B
Lz 恒量


l
由质心坐标公式，有
z
vi z′ ri r′ i rC x′
C
mi
y′ y
O
mi ri mrC 0
x
LC ri mi vir
§13-6 刚体的平面运动微分方程
LC J C
由质心运动定理和相对于质 心的动量矩定理，有：
y
Fn
y′
D
F2 F1
maC Fi ( e ) d (e) J C J C M C ( Fi ) dt
用于质点系的外力对质心的主矩 ，这就是质点系相对于质心(平移
系)的动量矩定理。

第12章——动量矩定理

第12章——动量矩定理

12.1 质点和质点系的动量矩
一、简单形状刚体的转动惯量 z
1. 均质细杆
设均质细杆长 l，质量为m，O
取微段 dx, 则
x
x
dx
l
dm mdx l
Jz
l m d x x2 1 ml2
0l
3
Jz1
l
2 l
2
m l
d
x
x2

1 12
ml 2
z1
x l C x dx
2
12.1 质点和质点系的动量矩
对点的：
LO MO(mv) ( miri )vC MO(mvC )
对轴的：
Lz M z (mvC )
12.1 质点和质点系的动量矩
4 定轴转动刚体对转动轴的动量矩
Lz M z (mivi ) miviri miri2
令 Jz＝Σmiri2 称为刚体对 z 轴的转动惯 量, 于是得
i 1
12.2 动量矩定理
上式左端为
n
i 1
d dt
MO (mivi )
d dt
n i 1
MO (mivi )
d dt
LO
于是得
d
dt
LO

n i 1
MO (Fi(e) )
质点系对某固定点O的动量矩对时间的导数，等 于作用于质点系的外力对于同一点的矩的矢量和。
12.2 动量矩定理
设作用在刚体上的外力可向质
心所在平面简化为一平面力系，由
y y'
质心运动定理和相对质心的动量矩 定理得
D

C
x'
maC F (e)

理论力学第14章动量矩定理

理论力学第14章动量矩定理

J yz J zy mi yi zi
（e）
如果对某坐标系所有惯性积均为零，则三根坐标轴称为刚体过
O
点的惯量主轴，相应的转动惯量称为主转动惯量。 如果惯量主轴还通过刚体质心，则称为中心惯量主轴。
14.3 矩心为质心的动量矩定理 14.3.1质点系对质心的动量矩定理 １．质点系对质心动量矩的定义
d r mv r F dt
(c)
(14-3)
d m yz zy yFz zFy dt d m zx xz zFx xFz dt
d m xy yx yFz zFy dt
动量矩定理
（图14-6）。
图14-6 柯尼希坐标系
或 z 都是反映刚体质量分布情况的物理量。
J z x 2 y 2 dm
（14-1 )dm J x ( y 2 z 2 )dm
（14-19b）
图14-3转动惯量的定义
图14-4 转动惯量的平行轴定理
２. 平行轴定理 J ( x y )dm ( x a )
第14章 动量矩定理
14.1 矩心为定点的动量矩定理 14.1.1 质点的动量矩定理
动量对空间某点或某轴线，叫做动量矩，也叫角动量
LO r p
p对
(14-1) (14-2a) (14-2b) (14-2c)
x, y, z 轴的动量矩则为
LOx m yz zy
LOz m xy yx
ΓO r I
叫冲量矩。故质点动量矩的变化，等于外力在该时间内给予该质点的冲量矩。
(14-7b)
14.1.2 质点系对定点的动量矩定理 L r m r (14-8)

第三章动量矩定理

第三章动量矩定理

1 2 Jz = ml 12
1 2 3 ρz = l = l 12 6
B 匀质薄圆环对于中心轴的转动惯量： 匀质薄圆环对于中心轴的转动惯量：
Jz =
∫
m
0
R dm = mR
2
2
Jz = m 2 R
C 匀质薄圆板对于中心轴的转动惯量： 匀质薄圆板对于中心轴的转动惯量：
ρz = R
m = 2πr dr ⋅ ρA i i i m 式中： ρA = 2
Jxy = ∑ xy m
分别称为刚体对轴y和 , 分别称为刚体对轴 和z,对轴 z和x以及对轴 和y的惯性积。 以及对轴x和 的惯性积。 和 以及对轴 惯性积可正、可负， (2) 惯性积可正、可负，也可等 于零（转动惯量永远是正） 于零（转动惯量永远是正）。
刚体对任意轴的转动惯量 把式（1）和式 和式（2）代入（a）式最后得 代入（ 把式 和式 代入 ） 刚体对于轴OL的 刚体对于轴OL的转动惯量 J = Jx cos2 α + Jy cos2 β + Jz cos2 γ
M o (mv) = ml 2ω sin θ
方向同上 故有： Lo = 2ml
2
ω sin θ
若考虑杆子的质量，则需要进行积分。
3.平动刚体对固定点的动量矩 平动刚体对固定点的动量矩 设刚体以速度v平动，刚体内任一点A的矢径 是 ri ,该点的质量为mi，速度大小是 vi 。 该质点对点O 的动量矩为 MO(mivi) = ri ×mivi LO =∑ MO(mivi) = ∑ ri ×mivi 因为刚体平动 v i= v = v C
2.质点系动量矩的计算 质点系动量矩的计算
◆质点系对点的动量矩：
LO = ∑MO(mivi) =∑r × mivi

理论力学_12.动量矩定理

理论力学_12.动量矩定理
理论力学
动量定理： 质心运动定理：
dp dt


F
(e) i
M aC

Fi
(e)
质点、质点系 动量的改变—外力（外力系主矢）
质心的运动—外力（外力系主矢） 若当质心为固定轴上一点时，vC=0，则其动量恒等于零， 质心无运动，可是质点系确受外力的作用。 动量矩定理建立了质点和质点系相对于某固定点（固轴） 的动量矩的改变与外力对同一点（轴）之矩两者之间的关系。
取固结于质心的平动参考系， 由速度合成定理，有
所以 由于 故
LC

ri m i v
i
即：质点系对质心的绝对运动动量矩，等于质点系对随质 心平动的参考系的相对运动动量矩。
结论：在计算质点系对于质心的动量矩时，用质点相对于 惯性参考系的绝对速度vi，或用质点相对于固结在质心上的 平动参考系的相对速度vi`，所得结果是一样的。 l
LO
1 P 2 g
代入 , 得
r
g
2
( P A PB
P 2
)
由动量矩定理：
d r2 P [ ( P A PB )] ( P A PB ) r dt g 2
PA PB d g dt r PA PB P /2
§8-3 动量矩守恒
动量矩定理：内力不会改变质点系的动量矩，只有外力才 能改变质点系的动量矩。 质点系的动量矩守恒 当
质点绕某心（轴）转动的问题。
二．质点系的动量矩定理 对质点Mi ：dt
d m O (m iv i ) m O ( Fi
d dt m O (m iv i )
()
) m O ( Fi
(i)
(e)

理论力学10动量矩定理

理论力学10动量矩定理
3D空间应用
在更高维度的空间中，动量矩定理可以通过向量的外积和叉积进行推广，适用于描述更复杂系统的动量矩变化。
n维空间推广
定理在更高维度空间的应用
多体系统
动量矩定理可以应用于多体系统，描述多个刚体之间的相互作用和运动关系，为多体动力学提供了基础。
非惯性参考系
在非惯性参考系中，动量矩定理需要考虑科里奥利力和离心力等因素的影响，以准确描述系统的动量矩变化。
定理证明的思路
在证明过程中，需要引入质点的质量、速度、位置矢量等概念，以及力、力矩等物理量。
引入相关概念
根据物理定律和数学公式，进行详细的数学推导，包括向量的点乘、叉乘等运算。
进行数学推导
经过推导，得出动量矩定理的结论，即质点系的动量矩等于外力矩对时间的积分。
得出结论Βιβλιοθήκη 定理证明的过程通过证明，得出的动量矩定理表述为：质点系的动量矩等于外力矩对时间的积分。
力矩的作用
力矩是描述力对物体运动轴的转动效应的物理量。在动量矩定理中，力矩的作用是改变物体的动量，即改变物体的运动状态。
时间和空间的影响
动量矩定理不仅涉及到物体的运动状态（动量和速度），还涉及到时间的变化率（即加速度），以及力作用的空间效应（即力矩）。因此，这个定理全面地描述了物体在空间和时间中的运动规律。
定理的物理意义
02
CHAPTER
定理的证明
首先明确动量矩定理的定义和意义，即对于一个质点系，其动量矩与外力矩之间的关系。
引入动量矩定理
建立证明框架
推导定理的表达式
根据定理的证明需求，建立证明的框架，包括定义、假设、推导和结论等部分。
根据牛顿第二定律和动量定理，推导出动量矩定理的表达式。
03

第九章 动量矩定理

第九章 动量矩定理

LZ =
∑M
Z
(mi v i )
质点系对点O的动量矩矢在通过该点的 轴上 质点系对点 的动量矩矢在通过该点的z轴上 的动量矩矢在通过该点的 的投影等于质点系对于该轴的动量矩。 的投影等于质点系对于该轴的动量矩。
[LO ]Z
= LZ
4
刚体平移时 可将全部质量集中于质心， 刚体平移时，可将全部质量集中于质心，作为一个 质点计算其动量矩。 质点计算其动量矩。 刚体转动时 刚体转动时，刚体对转轴的动量 矩为
dLO = Labcd − LABCD = LCDcd − LABab
LCDcd 1 = qV ρ dt v2 r2 cosθ2 n
1 LABab = qV ρ dt v1 r cosθ1 1 n 1 dLO = qV ρ dt (v2 r2 cosθ2 − v1 r cosθ1) 1 n dLO MO (F ) = n = qV ρ(v2 r2 cosθ2 − v1 r cosθ1) 1
6
d d dr d × mv + r × ( mv ) M O ( mv ) = ( r × mv ) = dt dt dt dt
dr =v dt
则上式为
d (mv ) = F dt
d M O (mv ) = v × mv + r × F dt
因为 所以
v × mv = 0
r × F = M O (F )
dt
16
【例4 】已知 m JO， 1 m2 r ，2 ，不计摩擦。 ， m， ，1 r 不计摩擦。 求（1） α ） （2）O处约束力 F ） 处约束力 N （3）绳索张力 FT ， T ） F
1 2
17
解：1） LO = JOω + m v1r + m2v2r2 （ ） 1 1 = ω(JO + m1r 2 + m2r22 ) 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

思 考 题
11-1 质点系的动量按下式计算：
∑∑==c v M v m K
质点系的动量矩可否按下式计算
()()c z z z v M m v m m L
∑==
11-2 人坐在转椅上，双脚离地，是否可用双手将转椅转动 为什么
11-3 图示两轮的转动惯量相同。

在图（a ）中绳的一端受拉力G ，在图（b ）中绳的一端挂一重物，重量也等于G 。

问两轮的角加速度是否相同为什么
11-4 问在什么条件下，图示定滑轮（设为匀质圆盘）两侧绳索的
(a
思
考
题
思
考
题
G
M 2
1
思
考
题
11-5
图
I
拉力大小才能相等
11-5 如图所示的传动系统中，轮1的角加速度按下式计算对吗
2
11
1J J M +=
ε
11-6 如图示，已知3/2Ml J z
=，按下列公式计算'
z J 对吗
22
9732Ml l M I I z z =
⎪⎭
⎫
⎝⎛+=' 11-7 质量为M 的均质圆盘，平放在光滑的水平面上，其受力情况如图所示。

试说明圆盘将如何运动设开始时，圆盘静止，图中2R r =
11-8 一半径为R 的轮在水平面上只滚动而不滑动。

如不计滚动摩阻，试问在下列两种情况下，轮心的加速度是否相等接触面的摩擦力是
否相同（1）在轮上作用一顺时针转向的力偶，力偶矩为M ;（2）在轮心作用一水平向右的力P
,R
M P =
F
F
F
(a
(b
(c
思考题11-7图
思考题
习题
11-1 计算各质点系的动量对O点的动量矩，已知a、b、c、d各均质物体重Q，物体尺寸与质心速度或绕转轴的角速度如图示。

（e）、(f)中设物体A和B的重量均为P ，速度为v ，均质滑轮的重量为Q 。

11-2 如图示，均质圆盘，半径为R，质量为m。

细杆长l，绕轴O 转动，角速度为ω。

求下列三种情况下对固定轴O的动量矩。

（1）圆盘固结于杆；（2）圆盘绕A轴转动，相对于杆OA的角速度为ω-；（3）圆盘绕A轴转动，相对于杆OA的角速度也为ω。

11-3 小锤系于线MOA的一端，此线穿过一铅垂小管。

小锤绕管轴沿半径MC＝R的圆周运动，每分钟120转。

现将线段OA慢慢向下拉，
的长度，此时小锤沿半径C1M1=R/2的圆周运动。

使外面的线段缩短到OM
1
求小锤沿此圆周每分钟的转数。

题 11-2图
11-4 一半径为R ，重P 的均质圆盘，可绕通过其中心的铅垂轴无摩擦地旋转。

另一重P 的人由B 点按规律22at s = 沿到O 轴半径为r 的圆周行走。

开始时，圆盘与人静止，求圆盘的角速度和角加速度。

11-5 飞轮在力矩t M ωcos 0作用下绕定轴转动。

沿飞轮的轮幅有重量为P
的两等重物体，各作周期性运动。

问：距离r 应满足什么条件才能使飞轮以角速度ω匀速转动。

11-6 图示均质杆AB 长l ，重P 。

杆的B 端固连一重Q 的小球，大小不计。

杆上点D 连一弹簧，刚性系数为k ，使杆在水平位置保持平衡。

设初速度v 0＝0，求给小球B 一个铅直方向的微小位移0δ后，杆AB 的运
(b
(c
(d )
(e )
(f )
题
11-1A
C O
题11-3图
题11-4题 11-2图
动规律。

11-7 一框架AA ，以细绳悬挂如图，它对竖直轴线OO 的转动惯量为J 1，在框架中间支承一转子，它对轴的转动惯量为J 2，开始时框架不动，转子有一角速度0ω，由于有摩擦，框架被带着转动。

若通过t 秒，转子与框架的角速度相同。

细绳的阻力扭矩可略去不计，求转子支承处的摩擦力矩。

11-8 图示离心式空气压缩机的转速为n =8600r/min ,每分钟容积流量为min /m Q 3370=,第一级叶轮气道进口直径为D 1＝，出口直径为D 2＝。

气流进口绝对速度v 1＝109m/s ，与切线成角︒=901α；气流出口绝对速度v 2＝183m /s ,与切线成角13212'= α。

设空气密度ρ＝m 3，试求这一级叶轮的转矩。

11-9 物体D 被装在转动惯量测定器的水平轴AB 上，这轴上还固连有半径为r 的鼓轮E ，缠在鼓轮上细绳的下端挂有质量为M 的物体C 。

已知物体C 被无初速地释放后，经过时间T 秒落下的距离是h ；试求被
题 11-5
O
O
A
题 11-6
题 11-7
题 11-9
题 11-8
测物体对转轴的转动惯量J 。

已知轴AB 连同鼓轮对自身轴线的转动惯量是J 0。

设物体D 的质心在轴线AB 上，摩擦和空气阻力都可略去不计。

11-10 高炉运送矿石用的卷扬机如图示。

已知鼓轮的半径为R ，重量为P ，在铅直平面内绕水平的轴O 转动。

小车和矿石总重量为Q ，作用在鼓轮上的力 矩为M ，轨道的倾角为α。

设绳的重量和各处的摩擦均
忽略不计，求小车的加速度。

11-11 电绞车提升一重m 的物体。

在其主动轴上有一不变的力矩M 。

已知：主动轴与从动轴和连同安装在这两轴上的齿轮以及其它附属零件的转动惯量分别为J 1和J 2 ，传动比K Z Z =12:；吊车缠绕在鼓轮上，此轮半径为R 。

设轴承的摩擦以及吊索的质量均略去不计，求重物的加速度。

11-12 两个物体A 和B 的质量各为m 1和m 2，且m 1>m 2，分别挂在两条不可伸长的绳子上，此两绳分别绕在半径为r 1和r 2的塔轮上，物体受重力的作用而运动。

试求塔轮的角加速度及轴承的反力。

塔轮的质量与绳的质量均可忽略不计。

11-13 圆轮A 重P 1，半径为r 1，以角速度ω绕OA 杆的A 端转动，此时将轮放置在重P 2的另一圆轮B 上，其半径为r 2。

B 轮原为静止，但
题 11-10 题 11-11 题 11-12
x
O
B P
题11-13题题11-15
可绕其几何轴自由转动。

放置后，A 轮的重量由B 轮支持。

略去轴承的摩擦与杆OA 的重量，并设两轮间的摩擦系数为f 。

问自A 轮放在B 轮上到两轮间没有滑动为止，经过多少时间
11-14 轮子的质量m ＝100kg ，半径R ＝1m ，可以看成均质圆盘。

当
轮子以转速n ＝120r/min 绕定轴C 转动时，在杆A 点垂直地施加常力P
，
经过10s 轮子停转。

设轮与闸块间的动摩擦系数f '＝，试求力P
的大小。

轴承的摩擦和闸块的厚度忽略不计。

11-15 已知图示均质三角形薄板的质量为?m ，高为h ，求对底边的转动惯量x J 。

11-16 图示连杆的质量为m ，质心在点C 。

若AC ＝a ，BC ＝b ，连杆对B 轴的转动惯量为B J 求连杆对A 轴的转动惯量。

11-17 均质钢制圆盘如图示，外径D ＝60cm ，厚h ＝10cm 。

其上钻有四个圆孔，直径均为d 1＝10cm ，尺寸d ＝30cm 。

钢的密度取ρ＝⨯－3
kg/cm 3,求此圆盘对过其中心O 并与盘面垂直的轴的转动惯量。

11-18 均质圆柱体A 的质量为m ，在外圆上绕一细绳，绳的一端B 固定不动，如图所示。

圆柱因解开绳子而下降，其初速为零。

求当圆柱体的轴心降落了高度h 时轴心的速度和绳子的张力。

11-19 一个重为P 的物块A 下降时，借助于跨过滑轮D 而绕在轮C 上的绳子，使轮子B 在水平轨道上只滚动而不滑动。

已知轮B 与轮C 固连在一起，总重为Q ，对通过轮心O 的水平轴的回转半径为ρ，试求物块A 的加速度。

11-20 滑轮A 、B 重为Q 1、、Q 2，半径分别为R 、r , r ＝2
R。

物体C
重P 。

作用于A 轮上的力矩M 为一常量。

试求C 上升的加速度。

A 、B 轮
题11-17图 题11-16图 题11-18图
可视为均质圆盘。

11-21 图示均质杆AB长为l，质量为m，放在铅直平面内，杆的一端A靠在光滑的铅直墙上，另一端B放在光滑的水平地板上，并与地板面成
角。

此后，令杆由静止状态倒下，求：（1）杆在任意位置时的角速度和角加速度。

（2）当杆脱离墙时，此杆与水平面的夹角。

11-22 长l，重W的均质杆AB和BC用铰链B联结。

并用铰链A固定，位于平衡位置如图所示。

今在C端作用一水平力F ，求此瞬时，两杆的角加速度。

题11-19图题11-20图题11-21图题11-22图。