专题三:液面升降的问题
- 格式:ppt
- 大小:621.00 KB
- 文档页数:6


巧解“液面升降”问题湖北省荆门市漳河中学曾祥俊学习完初中物理《浮力》这一部分内容后,常常会遇到有关“液面上升还是下降”的讨论的题目。
这类题若用常规方法解答,很繁锁,且容易出错,但采用如下方法解答,既快捷,又不易出错。
基本解答思路:液面的升降由过程前后的排开液体的体积决定,即V排变大,液面上升;V排变小,液面下降;V排不变,液面不变。
根据阿基米德原理有:V排=F浮/(ρ液g),此类题中ρ液一般不会变,这样就可以把讨论V排的变化转化成讨论F浮的变化,即过程前后F浮变大,液面上升;F浮变小,液面下降;F浮不变,液面不变。
而根据浮沉条件讨论浮力的变化相对而言要简单多了,这样问题就得到了简化。
下面就举几个例子来谈谈具体的巧解过程。
例一、在一装水的大烧杯中浮有一小盒,且盒中有几粒小石子,当把盒中的小石子取出投入烧杯的水中,静止时,烧杯的水面是上升了还是下降了?巧解:过程前,盒子和石子作为一个整体漂浮在水面上,根据漂浮条件有F浮1=G总=G盒+G石.过程后,盒子漂浮在水面上,所以有F浮盒=G盒,石子在水中下沉,所以有F浮石<G石,总体浮力F浮2=F浮盒+F浮石<G盒+G石,即F浮1>F浮2,所以水面下降。
例二、一块纯冰漂浮在一装水的烧杯中静止,当冰完全化成水后,烧杯中的水面如何变化?巧解:过程前,冰块漂浮在水面上,所以有F浮1=G冰,过程后,(假设冰化成水后仍成团没有散开)此“水团”在水中应悬浮(密度相等悬浮),所以然有F浮2=G水团(悬浮时浮力等于重力),又冰化成水质量不变,所以有F浮2=G冰,即F浮1=F浮2,所以水面保持不变。
例三、若在例二中,纯冰中有一气泡,情况又如何?巧解:过程前,冰块漂浮在水面上,所以有:F浮1=G冰+G泡。
过程后,气泡在水中静止时肯定是漂浮,因此有F浮2=F浮水团+F浮气泡=G水团+G泡=G冰+G泡,即F浮1=F浮2,所以水面保持不变。
例四、若例二中,冰中有杂质,如“木屑”或“沙子”,情况又分别如何?巧解:(1)当冰中杂质是木屑时,过程前,F浮1=G总=G木屑+G冰(漂浮时浮力等于重力),过程后,冰化成水,“水团”在水中是悬浮,F浮水团=G水团=G冰,木屑在水中应漂浮,F浮木屑=G木屑,所以总体浮力F浮2=G冰+G木屑,即F浮1=F浮2,所以水面保持不变。
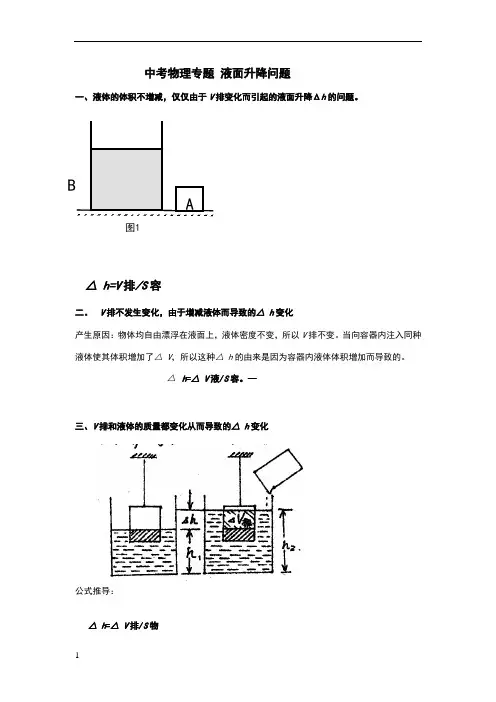
中考物理专题液面升降问题一、液体的体积不增减,仅仅由于V排变化而引起的液面升降Δh的问题。
BA图1△ h=V排/S容二. V排不发生变化,由于增减液体而导致的△ h变化产生原因:物体均自由漂浮在液面上,液体密度不变,所以V排不变。
当向容器内注入同种液体使其体积增加了△ V,所以这种△ h的由来是因为容器内液体体积增加而导致的。
△h=△ V液/S容。
--三、V排和液体的质量都变化从而导致的△ h变化公式推导:△ h=△V排/S物△ h =△ V 液/(S 容-S 物)四.如图1和2所示:当物体相对液面移动的距离为△h 时,液面上升的距离为△H, 则:△hS 物=S 容△H ,V 总1=V 水+h 1S 物 = H 1S 容 ① V 总2 =V 水+h 2物 = H 2S 容 ② 所以②-①.得:△hS 物=S 容△H五.如图3和图4中,当物体相对容器移动的距离为△h 时,液面上升的距离为△H,则:△hS 物=△H (S 容—S 物),Hh图1hH图2Hh1图3h2图4因为 V 总1=V 水+(H 1—h 1)S 物 = H 1S 容 ①V 总2=V 水+(H 2—h2)s 物=H 2 S 容 ②所以②-①.得:△hS 物=△H (S 容—S 物)中考演练:东城一模如图所示,底面积为S b 的圆柱形容器内盛有适量的水,另一底面积为S a的圆柱体A 有部分体积浸在水中,当圆柱体A 相对于容器下降高度为h 时,水没有溢出,圆柱体A 也未全部没入水中,物体A 所受水的浮力增加了 。
中考演练:朝阳二模12.如图7甲所示,装有部分水的试管竖直漂浮在容器内的水面上,试管内水面与容器底部的距离为h ,试管壁粗细均匀、厚度不计;现将一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好仍为h ,如图8乙所示,若试管横截面积与容器横截面积之比为1:5,则下列说法正确的是 A .放入的物块密度为5×103kg/m3 B .放入的物块密度为×103kg/m3 C .放入的物块密度为×103kg/m3 D .小试管与容器内水面变化的高度相等2014海淀一模14. 如图8所示,水平桌面上放有甲、乙、丙、丁四个完全相同的圆柱形容器。

液面升降问题 Prepared on 22 November 2020液面升降问题分析液面升降的主要类型有:1、纯冰在纯水中熔化;2、纯冰在盐水(或其它密度比水大的液体)中熔化;3、纯冰在密度比水小的液体中熔化;4、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化;5、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化;6、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化;7、一块冰漂浮在容器的水面上,冰块中含有一定质量的气体(空气、氢气、二氧化碳),当冰完全熔化后,容器中的水面如何变化例1:有一块冰浮在容器的水面上,当冰块完全熔化后,水面高度将怎样变化解:冰块熔化前排开水的体积(即图中斜线部分)为:V排=F浮/ρ水g=G冰/ρ水g=m冰/ρ水(∵漂浮时F浮=G冰)冰块化成的水的体积为:V=m水/ρ水=m冰/ρ水(∵冰化成水后质量不变m冰=m水)所以液面高度不变推论:纯水水面上浮有纯冰.当冰熔化时液面将不变。
当冰熔化时,水对容器底的压强不变。
例2:若一冰块在水中,冰块与容器底部相接触并相互间有压力,则当冰块完全熔化后,容器内的水面将怎样变化解析:冰块没有漂浮在水面上,冰块所受浮力小于冰块所受重力,所以熔化前F浮<G冰,而F浮=G 排ρ水gV排,即ρ水gV排<G冰,故得V排<G冰/(ρ水g)熔化为水的体积V水=m水/ρ水=m冰/ρ水=G冰/(ρ水g)所以V排<V水,即熔化后水面要上升。
例3:有一块冰漂浮在一杯浓盐水中(冰的密度是0.9×103千克/米3;浓盐水的密度是1.1×103千克/米3).如果冰块全部熔化后,则()A.液面不变B.液面上升C.液面下降D.无法判断解析:冰块熔化前,在盐水中处于漂浮状态.则有F浮=G,即ρ盐gV排=m冰gV排=m冰/ρ盐 (1)冰块熔化后,排开液体的体积等于冰熔化成水的体积,即V’排=V水=m水/ρ水(∵冰化成水后质量不变m冰=m水,m水/ρ水=m冰/ρ水) (2)比较冰块熔化前与冰块熔化后排开液体的体积可得m冰=m水,ρ水<ρ盐。

液面升降问题考查要点液面升降问题是中考压轴题的考查热点,近三年(2014-2016年)的中考压轴题都是考查这方面的问题,以液体的压强和浮力为载体,考查学生对液体压强、浮力知识的综合运用能力。
解题思路利用量筒的原理1.基本思路:【例1】如图17-1所示,容器内分别装有水和盐水,在液面上浮着一块冰,问:(1)冰在水中熔化后,水面如何变化?(2)冰在盐水中熔化后,液面如何变化?(a)(b)图17-1【思路点拨】容器中的液面高度变化是由于容器中物体排开液体的体积与液体体积之和发生变化引起的。
根据,因容器内原来的水的体积不变,关键是比较两个体积,一个是冰熔化前,排开水的体积,一个是冰熔化成水后,水的体积。
求出这两个体积,再进行比较,就可得出结论。
【解】(1)如图(a)所示,冰在水中,熔化前处于漂浮状态。
===①冰熔化成水后,质量不变:=求得:==②比较①和②,=也就是冰熔化后体积变小了,恰好占据了原来冰熔化前在水中的体积。
所以,冰在水中熔化后液面不变(2)冰在盐水中:冰熔化前处于漂浮,如图(b),则===③冰熔化成水后,质量不变,推导与问题(1)相同。
=④比较③和④,因为<所以>也就是冰熔化后占据的体积要大于原来冰熔化前在盐水中的体积。
所以,冰在盐水中熔化后液面上升了。
【答案】(1)冰在水中熔化后液面不变。
(2)冰在盐水中熔化后液面上升。
【变式练习】冰放在密度小于冰的液体中,静止后处于什么状态,熔化后,液面又如何变化?【例2】如图17-2所示,底面积为的圆柱形容器内盛有适量的水,另一底面积为的圆柱体A有部分体积浸在水中,当圆柱体A相对于容器下降高度为h时(水没有溢出,圆柱体A也未全部没入水中),求:容器中液体高度的变化量?图17-2【思路点拨】解法一:画出情境图,如图17-3所示,找出体积之间的关系图17-3即:①Δh②②-①可得Δh因为所以ΔhhΔh=。
解法二:如图17-4,圆柱体下降h后,体积为的水被挤走,图17-4水被挤到原水面上圆柱体周围的区域,体积为Δh所以h解得Δh=。

对浮力中液面升降问题的探究液体中的浮力是指物体浸泡在液体中受到的向上的力。
当物体完全或部分浸入液体中时,液体对物体的压力会导致物体受到一个向上的浮力,这个浮力的大小等于物体排开的液体的重量。
浮力的大小可以通过阿基米德定律来计算:浮力等于排开的液体重量,即F_b=ρVg,其中F_b为浮力,ρ为液体的密度,V为物体排开液体的体积,g为重力加速度。
当液体中的液面升降时,测量物体浮力的方法有很多种,下面我们就根据不同情况进行探究。
情况一:液体容器固定不动,液面升降。
在这种情况下,液体容器固定不动,因此液体容器内的液体体积不变。
根据阿基米德定律,物体受到的浮力等于物体排开的液体的重量,所以液面升降并不会对浮力产生影响。
例如,当我们在一个装满水的容器中放入一个物体,物体会受到一个向上的浮力。
当我们升高液面时,液体的密度和物体排开的液体体积都不会改变,所以浮力的大小也不变。
同样,当我们降低液面时,浮力的大小仍然保持不变。
情况二:液体容器可以移动,液面升降。
在这种情况下,液体容器可以移动,液体容器内的液体体积会随之改变。
此时,液面升降会对浮力产生影响。
当液面升高时,液体密度和物体排开的液体体积都不变,所以浮力的大小也不变。
但是,由于液体容器也随之上升,液体容器内的液体的重力势能增加,而根据能量守恒定律,液体容器内的液体的重力势能增加需要从其他地方得到能量,这个能量来自物体受到的浮力。
因此,在液面升高时,浮力的一部分会用于提供液体容器上升所需的能量,从而导致浮力减小。
同样地,在液面降低时,液体容器内的液体的重力势能减小,液体容器下沉,能量会转化为物体受到的浮力,这样浮力就增大了。
综上所述,当液体容器可以移动时,液面升降会对浮力产生影响。
液面升高时,浮力减小;液面降低时,浮力增大。


液面升降问题类专题类型一:容器中的固态物质投入水中后判断液面升降例题1: 情景如图1所示,小船和石块一起漂浮在水中,将石块(或金属块)从船中取出放入水中后,你观察到的现象是水面。
分析:【练习】1、如图2所示,一个小船中放有ABC三个小球,小船和球一起漂浮在水面上,其中A 球密度小于水,B球密度等于水,C球密度大于水,小船可以自由的漂浮在水面上。
(1)只将A球放入水中,则A球(填浮沉状况),液面(填“上升”或“下降”或“不变”)(2)只将B球放入水中,则B球(填浮沉状况),液面(填“上升”或“下降”或“不变”)(3)只将C球放入水中,则C球(填浮沉状况),液面(填“上升”或“下降”或“不变”)(4)若将ABC三球同时从船中取出放入水中,则液面(填“上升”或“下降”或“不变”)。
2、如果将沉在水底的石块放入船中使船漂浮,液面将。
3、水槽中放一个小铁盒,铁盒中放少许细线和一个铝块,铁盒漂浮在水面。
现用细线把铝块拴在铁盒下面,铁盒仍漂浮在水面,如图3所示。
讨论此时水槽中的水位以及铁盒浸入水中的体积,说法正确的是()A.水槽中水位不变,铁盒浸入水中的体积变大B.水槽中水位下降,铁盒浸入水中的体积不变C.水槽中水位不变,铁盒浸入水中的体积变小D.水槽中水位上升,铁盒浸入水中的体积不变类型二:纯冰浸于液体,熔化后判断液面升降分析:1.冰块放在水中,漂浮,熔化后,液面。
简单推导过程:2.冰块放在盐水中,漂浮,熔化后,液面。
简单推导过程:3.冰块放在煤油(或酒精)中,沉底,熔化后,液面。
简单推导过程:类型三:如图4冰块中含有其它物体浮于水中,冰块熔化后判断水面升降。
分析:【练习】1.冰块内包有一个石块(石块密度大于水的密度)漂浮在水面上,冰块熔化后,石块(填浮沉状况),则水面(填“上升”或“下降”或“不变”)。
2.冰块内包有一个密度等于水的物体漂浮在水面上,冰块熔化后,水面(填“上升”或“下降”或“不变”)。
图43.冰块内包有一个木块(木块密度小于水)漂浮在水面上,冰块熔化后,水面(填“上升”或“下降”或“不变”)。
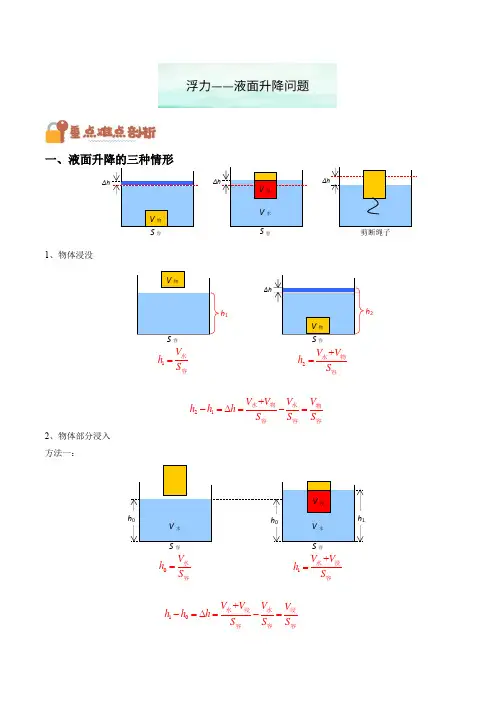


甲乙丙40 h /cm50 60 F /N20 30 0 4 2610 8 1070 液面升降问题△h 的大小指液面高度的变化量,它是浮力问题与液体压强综合计算题的结合点。
液面升降的高度Δh 根据产生的原因大致可分为三类:一、液体的体积不增减,仅仅由于V 排变化而引起的液面升降Δh 的问题。
二、V 排可能发生变化,由于增减液体而导致的△ h 变化 三、V 排和液体的质量都变化从而导致的△ h 变化例题1:如图所示,底面积为S b 的圆柱形容器内盛有适量的水,另一底面积为S a的圆柱体A 有部分体积浸在水中,当圆柱体A 相对于容器下降高度为h 时,水没有溢出,圆柱体A 也未全部没入水中,物体A 所受水的浮力增加了 。
例题2:如图甲所示,圆柱形平底容器置于水平桌面上,其底面积为500cm 2。
在容器内放入一个底面积为200cm 2、高为20cm 的圆柱形物块,物块底部的中心通过一段细线与容器底部相连。
向容器内缓慢注入某种液体直至将其注满,如图乙所示。
已知在注入液体的过程中细线对物块的拉力F 随液体深度h 的变化关系图像如图丙所示。
若将细线剪断,当物块静止时,液体对容器底部的压强为 Pa 。
(g =10N/kg )例题3:如图甲所示,装有部分水的试管竖直漂浮在容器内的水面上,试管内水面与容器底部的距离为h ,试管壁粗细均匀、厚度不计;现将一物块完全浸没在该试管水中,发现试管内水面与容器底部的距离恰好仍为h ,如图乙所示,若试管横截面积与容器横截面积之比为1:5,则下列说法正确的是( ) A .放入的物块密度为5×103kg/m 3 B .放入的物块密度为1.25×103kg/m 3 C .放入的物块密度为2.25×103kg/m 3 D .小试管与容器内水面变化的高度相等专项训练(一)1.如图9甲所示,A B 、两个实心正方体所受重力分别为A B G G 、,它们的密度分别为A B ρρ、,它们的边长分别为A B h h 、.若将它们放在水平地面上,对地面产生的压强分别为A B p p 、.若将它们放入柱状容器的水中(水未溢出),物体静止后,如图9乙所示,A 物体有1/3的体积露出水面,B 物体静止在水中,容器底部受到的压力比未放入两物体时增加1F ;若将B 物体取出轻压在A 物体上(水未溢出),待物体静止后.容器底部受到水的压力比未放入两物体时增加2F .若已知2A B p p =,甲 乙1 1.52N F =,g 取10N/kg .则下列说法正确的是( )A .:3:1AB h h =B .200Pa A B p p -=C .0.04m B h =D .211.52N A B G G F F +==;2.一个竖直放置在水平桌面上的圆柱形容器,内装某种液体。
2024届中考物理专题复习:液面升降问题 教学设计一、教学目标学生通过微课的学习,在物体浸入或移出液体的情景中,能根据题目条件找到计算液面深度变化量的方法。
二、教学重难点本课重点在于教会学生通过画草图找液面升降过程的体积关系,掌握计算液面深度变化量的两种方法,明确两种方法适用条件的不同。
本课难点在于理解两种计算方法的推导过程,将采用直观的图形分析帮助学生理清体积关系。
另一难点是将本课学到的计算方法应用到更复杂的题目中,做到“合理拓展”和“举一反三”,将在作业设计上采用拓展练习和引导归纳总结的方式帮助学生突破难点。
三、教学过程1.引入近几年的中考题中高多次出现“物体浸入液体”或“物体移出液体”的模型,很多同学的丢分点出现在计算液面深度变化量,特别是在“除以容器底面积还是容器和物体底面积之差”这个问题上纠结不清,这恰好也是关键步骤,今天我们就通过微课的学习彻底解决这个问题。
2.两种方法的推导例题:如图所示,水平桌面上有一底面积为S 容的圆柱形容器,容器中装有一定量的水,现提着一底面积为S 物的圆柱体铁块置于水面上方,恰好接触到水面,现在使铁块下移h 的距离,求液面深度的变化量△h 。
解题方法:画出浸入后的草图,对比浸入前的图分析其中的体积关系。
根据图中标注的体积序号分析得出:③②①V V V += h S S h S ∆-=)(物容物 物容物S S hS h -=∆拓展解法:④①排V V V +=∆ ④③②排V V V V ++=∆ hS V ∆=∆容排容排S V h ∆=∆ 3.总结:根据题目条件,若容易找到下移距离,则用第一种方法。
若容易找到下移后浸入液体中的长度或可直接算出△V 排,则用第二种方法。
四、配套练习设计目标1.如图甲所示,水平桌面上有一底面积为200cm 2的圆柱形容器,容器中装有一定量的水,现提着一底面积为100cm 2的圆柱体铁块置于水面上方,恰好接触到水面,按以下方式进行操作:(1)如图乙,使铁块下移10cm ,求水面上升的高度。
•专题液面升降问题1. 组合物体漂浮类型要看液面是上升还是下降,关键是比较前后两次物体排开液体的体积的变化。
设,后来排开液体的体积为V‘排,若V’排>V排,物体原来排开液体的体积为V排则液面上升,若V’排<V排,则液面下降;若V’排=V排,则液面高度不变,又根据阿基米德原理知,物体在液体中所受的浮力,故,因为液体的密度ρ液不变,固物体的排开液体的体积取决于物体所受的浮力,所以只要判断出物体前后所受浮力的变化情况,即可判断出液面的升降情况。
例1一个水槽内漂浮着一个放有小铁球的烧杯,若将小铁球取出放入水槽里,烧杯仍漂浮在水槽中,则水面将( )A.上升 B.不变 C.下降 D.无法判断解析:铁球和烧杯漂浮在水中,装有铁球的烧杯所受的浮力F与烧杯和铁球的总浮重力平衡,则有:。
把铁球放入水槽中,铁球下沉,铁球单独受到的浮力,;烧杯单独受到的浮力为。
铁球放入水槽中后,铁球和烧杯所受浮力之和为F,因此,烧杯和铁球后来排浮2开水的体积之和小于原来排开的水的体积,所以水面下降,故正确选项为C。
2.纯冰熔化类型:此类题的规律技巧:若冰块漂浮于水中,则冰熔化后液面不变;若冰块漂浮于密度大于水的液体中,则冰熔化后液面上升;若冰块漂浮于(或浸没于)密度小于水的液体中,则冰熔化后液面下降。
要判断液面的升降,必须比较冰排开液体的体积与冰熔化成水的体积之间的关系。
冰未熔化时,若它漂浮在液面上,则所受的浮力与重力相等,即。
冰块所受的,冰块的重力,由此可得;冰熔化后,化成水的体积。
所以当冰块漂浮于水中时,,液面不变;当时,,液面上升。
若冰块浸没液体中,则冰块排开液体的体积等于冰块的体积,而冰熔化后的体积小于冰的体积,故液面下降。
例2如图所示,烧杯中的冰块漂浮在水中,冰块上部高出杯口,杯中水面恰好与杯口相平,待这些冰全部熔化后( )A.将有水从杯中溢出B.不会有水从杯中溢出,杯中水面也不会下降C.烧杯中水面下降D.熔化过程中水面下降,完全熔化后有水溢出解析:冰熔化后烧杯中的水面将保持不变,故不会有水溢出3.一块各种姿态熔化的冰块,一个升降变化的水平面常规方法:对于类型1,漂浮在水中的冰块完全熔化后,水面高度如何变化的问题,介绍一下常规方法。
中考复习专题之液面升降问题一、液面升降现象的各类和变化规律:A、纯冰在纯水中熔化——不变B、纯冰在盐水(或其它密度比水大的液体)中熔化——升高C、纯冰在密度比水小的液体中熔化——降低D、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化——不变E、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化——降低F、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化——升高。
(煤油最后露出水面的部分在水面散开,从而增加了液面的高度。
)二、解题思路:1.传统的常规解法,即比较变化前后两个排开液体体积的大小关系。
例1:有一块冰浮在容器的水面上,当冰块完全熔化后,水面高度将怎样变化?解:冰块熔化前排开水的体积为:V排=F浮/ρ水g=G冰/ρ水g=m 冰/ρ水∵漂浮时F浮=G冰冰块化成的水的体积为:V=m水/ρ水=m 冰/ρ水∵冰化成水后质量不变,所以液面高度不变(相当于冰块化成的水刚好填补满了排开的部分)例2:有一块冰中含有小石块,浮在容器的水面上,当冰块完全熔化后,水面高度怎样变化?解:熔化前排开水体积为:V排=F浮/ρ水g=G总/ρ水g=(G冰+G石)/ρ水g=(m冰+m石)/ρ水①熔化后的体积为冰化成的水的体积加上沉在容器底的石块的体积,即:V=V水+V石=m水/ρ水+m石/ρ石=m冰/ρ水+m石/ρ石②比较①②式,∵ρ石>ρ水,∴V<V排,所以液面下降。
例3:有一块冰中含有液态的煤油,浮在容器内的水面上,当冰块完全熔化后,液面将怎样变化?解:熔化前排开水体积为:V排=F浮/ρ水g=G总/ρ水g=(G冰+G油)/ρ水g=(m冰+m油)/ρ水①熔化后的体积为V=V水+V油=m水/ρ水+m油/ρ油=m冰/ρ水+m 油/ρ油②比较①②式,∵ρ油<ρ水,∴V>V排,所以液面上升。
2.全新的巧解思路:①因为此类题中容器的形状不影响最后的结论,因此可以把容器假想为柱体。
②柱体内装液体时,容器底所受到的总压力F总等于容器内所有物体受到的总重力,即:F总=G总。
【高中物理】液面升降问题分析液面升降的主要类型有:1、纯冰在纯水中熔化;2、纯冰在盐水(或其它密度比水大的液体)中熔化;3、纯冰在密度比水小的液体中熔化;4、含有木块(或其它密度比水小的固体)的冰块在纯水中熔化;5、含有石块(或其它密度比水大的固体)的冰块在纯水中熔化;6、含有煤油(或其它密度比水小的液体)的冰块在纯水中熔化;7、一块冰漂浮在容器的水面上,冰块中含有一定质量的气体(空气、氢气、二氧化碳),当冰完全熔化后,容器中的水面如何变化?例1:有一块冰浮在容器的水面上,当冰块完全熔化后,水面高度将怎样变化?解:冰块熔化前排开水的体积(即图中斜线部分)为:V排=F浮/ρ水g=G冰/ρ水g=m冰/ρ水(∵漂浮时F浮=G冰)冰块化成的水的体积为:V=m水/ρ水=m冰/ρ水(∵冰化成水后质量不变m冰= m水)所以液面高度不变推论:纯水水面上浮有纯冰.当冰熔化时液面将不变。
当冰熔化时,水对容器底的压强不变。
例2:若一冰块在水中,冰块与容器底部相接触并相互间有压力,则当冰块完全熔化后,容器内的水面将怎样变化?解析:冰块没有漂浮在水面上,冰块所受浮力小于冰块所受重力,所以熔化前F浮<G冰,而F浮=G排ρ水g V排,即ρ水g V排<G冰,故得V排<G冰/(ρ水g)熔化为水的体积 V水=m水/ρ水= m冰/ρ水= G冰/(ρ水g)所以V排<V水,即熔化后水面要上升。
例3:有一块冰漂浮在一杯浓盐水中(冰的密度是0.9×103千克/米3;浓盐水的密度是1.1×103千克/米3).如果冰块全部熔化后,则 ( )A.液面不变 B.液面上升 C.液面下降 D.无法判断解析:冰块熔化前,在盐水中处于漂浮状态.则有F浮=G,即ρ盐g V排=m冰gV排=m冰/ρ盐 (1)冰块熔化后,排开液体的体积等于冰熔化成水的体积,即V’排=V水= m水/ρ水(∵冰化成水后质量不变m冰= m水, m水/ρ水=m冰/ρ水) (2)比较冰块熔化前与冰块熔化后排开液体的体积可得m冰= m水, ρ水<ρ盐。
液面升降问题的分析冰浮于液面的问题是生活中的常见问题在各类试卷中经常出现,但由于这类问题的现象不太明显,观察需要的时间较长,不为一般的学生所重视.即使一部分学生有意识地去进行观察,出会现因为问题类型比较多,而结论只有“升”和“降”两种,常常出现而把现象和条件的对应关系混淆的现象,导致认识的偏差。
为了更深刻地理解引起液面“升”、“降”的原因,准确把握条件和现象之间的关系。
可以将各类问题进行分类处理,从最基本的漂浮在液面上的冰熔化成水后液面的升降问题为基点,逐步展开思考形成系统的认识。
更重要的是可以通过这些问题的讨论和思考,把许多有关物体浮沉及液面变化问题连成一个整体。
对于液体中的物体由于某种变化而引起的液面升降问题的形式出现,本文介绍一种简便快捷的判断方法——“状态法”.(一)、什么叫状态法所谓“状态法”,就是对变化前后液体中的物体所处的状态进行比较来判断液面的升降.(二)、如何用“状态法”速断液面升降①若变化前后液体中的物体都处于漂浮、悬浮状态,而无沉体出现,则液面不变;②若液体中的物体,在变化前无沉体,而变化后有沉体出现,则液面下降;③若液体中的物体,在变化前有沉体,而变化后无沉体出现,则液面升高.说明:变化前后液体中物体的总质量保持不变;容器中液体的密度不变.(三)、证明G,变化前后在液体中所受的总浮力分别为F浮、F浮′.若变化前后均无沉体出现,由浮沉条件知F浮′=F浮=G,ρ液gV排′=ρ液gV排,则V排′=V排,液面不变.若变化前无沉体,变化后有沉体,由浮沉条件知浮=G,F浮′<G,则F浮′<F浮,即V排′<V排,故液面下降.若变化前有沉体,变化后无沉体,由浮沉条件知F浮<G,F浮′=G,则F浮′>F浮,即V排′>V排,故液面上升.一、液面升降的主要类型有:类型一:纯冰浸于液体,熔化后判断液面升降1、纯冰在纯水中熔化;2、纯冰在盐水(或其它密度比水大的液体)中熔化;3、纯冰在密度比水小的液体中熔化;类型二:冰块中含有其它杂质,冰块熔化后判断水面升降。