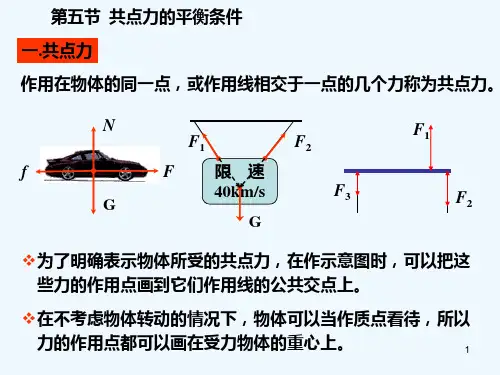
在竖直墙壁上,用斜向上的恒力按着一重为G的木块沿墙壁作匀速运动,F与竖直方向的夹角为θ,求滑动摩擦因数μ。
共点力作用下物体的平衡条件是:
第二步 建立适宜的坐标系,把不在坐标轴 FA 、FB 不断增大
假设逐渐添加C端所挂物体的质量,那么最先断的绳(
)
O
B
上的力用正交分解法分到坐标轴上。 第五节 共点力的平衡条件
第八页,共12页。
二、合成法:物体受几个力的作用,将某几 个力合成,将问题转化为二力
平衡。
5、正交分解法; 将物体所受的共点力正交分解,平衡条件可表 示为:
由 F合=0 得: X轴上合力为零 : Fx=0
y轴上合力为零 : Fy=0
第九页,共12页。
正交分解法的根本思绪;
第一步 进展受力分析,画出受力图。
摩擦因数为μ,那么木块遭到的滑动摩擦力为:
(
)
B、D
A. μmg
B. μ(mg+Fsinθ)
C. μ(mg-Fsinθ)
θ
D. Fcosθ
第七页,共12页。
在竖直墙壁上,用斜向上的恒力按着一重为G的 木块沿墙壁作匀速运动,F与竖直方向的夹角为θ, 求滑动摩擦因数μ。
F
F
f
θ
N
f
G
N G
GFcos Fs in
F合 = 0
共点力作用下物体的平衡条件是: 物体所受的合外力力为零
4、平衡条件的运用;
一、分解法:物体受几个力的作用,将某个
力按效果分解,那么其分力与 其
它在分力反方向上的力满足平
衡条件。〔动态分析〕
第六页,共12页。
质量为m的木块在与程度方向成θ角的推力F的作用