共点力平衡专题(课堂PPT)

格式：ppt
大小：670.00 KB
文档页数：29

下载文档原格式

共点力的平衡条件(共12张PPT)优秀

在竖直墙壁上，用斜向上的恒力按着一重为G的木块沿墙壁作匀速运动，F与竖直方向的夹角为θ，求滑动摩擦因数μ。
共点力作用下物体的平衡条件是：
第二步建立适宜的坐标系，把不在坐标轴 FA 、FB 不断增大
假设逐渐添加C端所挂物体的质量，那么最先断的绳(
)
O
B
上的力用正交分解法分到坐标轴上。第五节共点力的平衡条件
第八页，共12页。
二、合成法：物体受几个力的作用，将某几个力合成，将问题转化为二力
平衡。
5、正交分解法; 将物体所受的共点力正交分解，平衡条件可表示为：
由 F合=0 得： X轴上合力为零： Fx=0
y轴上合力为零： Fy=0
第九页，共12页。
正交分解法的根本思绪;
第一步进展受力分析，画出受力图。
摩擦因数为μ，那么木块遭到的滑动摩擦力为：
(
)
B、D
A. μmg
B. μ(mg+Fsinθ)
C. μ(mg-Fsinθ)
θ
D. Fcosθ
第七页，共12页。
在竖直墙壁上，用斜向上的恒力按着一重为G的木块沿墙壁作匀速运动，F与竖直方向的夹角为θ，求滑动摩擦因数μ。
F
F
f
θ
N
f
G
N G
GFcos Fs in
F合 = 0
共点力作用下物体的平衡条件是：物体所受的合外力力为零
4、平衡条件的运用;
一、分解法：物体受几个力的作用，将某个
力按效果分解，那么其分力与其
它在分力反方向上的力满足平
衡条件。〔动态分析〕
第六页，共12页。
质量为m的木块在与程度方向成θ角的推力F的作用

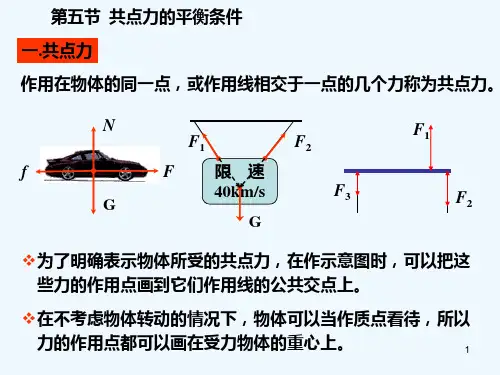
共点力的平衡条件-PPT

4
第五节共点力的平衡条件
3.在竖直墙壁上，用斜向上的恒力按着一重为G的木块沿墙壁作匀速运动，F与竖直方向的夹角为θ，求滑动摩擦因数μ。
F
θ
N
f
G
此题答案： G F cos
F sin
F
f
N
G
G F cos F sin
5
第五节共点力的平衡条件
4.如图所示，斜面倾角θ，木块M和斜面间滑动摩擦因数为μ，问物体m质量多大时，才能使木块匀速运动？。
A. μmg
B. μ(mg+Fsinθ)
θ
C. μ(mg-Fsinθ)
D. Fcosθ
此题答案： B、D
3
第五节共点力的平衡条件
2.某公园要在儿童乐园中建一座滑梯，已知斜面与物体间滑动摩擦因数μ= 0.75，那么倾角θ至少要多少度儿童在斜面上才可以由静止开始滑下？
要多少度？
此题答案：倾角θ至少要37°
第五节共点力的平衡条件一.共点力作用在物体的同一点，或作用线相交于一点的几个力称为共点力。
N
F1
F2
F1
f
F 限速
G
40km/s
F3
F2
G
❖为了明确表示物体所受的共点力，在作示意图时，可以把这些力的作用点画到它们作用线的公共交点上。
❖在不考虑物体转动的情况下，物体可以当作质点看待，所以
力的作用点都可以画在受力物体的重心上。
7
正交分解法
此方法是力学解题中应用最普遍的方法，应注意学习。
⑴共点力作用下物体的平衡条件是：F合= 0； ⑵在建立直角坐标系时，要考虑尽量减少力的分解。
正交分解法把矢量运算转化成标量运算，极大的降低了数学

共点力平衡专题 ppt课件

4及. 角确度定变未化知确量定大力小的、大方小向及的方变向化的变化情况. 应用条件:合力大小和方向都不变;一个分力的方向不变,分析另一个分力方向变化时两个分力大小的变化情况。用图解法具有简单、直观的优点。
→墙面挂绳变化
→图解法
动
结当绳子不断变短，论 FN增大，FT也增大
态
矢
量
三角
闭合
FT
B
A
αR
O
动态平衡中，合力不变两个分力的大小和方向均发生变化此类情景可选用三角形相似法
表面光滑、半径为 R 的半球固定在水平地面上，球心O 的正上方O′处有一无摩擦定滑轮，轻质
细绳两端各系一个小球挂在定滑轮上，如图所示。
两小球平衡时，若滑轮两侧细绳的长度分别为L1 ＝2.4R 和L2＝2.5R，则这两个小球的质量之比 m1∶m2为(不计球的大小) ( D )
三、常见应用题型：
2.共点力的作用下动态平衡
动态平衡的常见问题：
动态分析极值分析临界问题
2.共点力的作用下动态平衡常见问题
动态分析问题
物体状态发生缓慢变化过程中始终处于一系列的平衡状态，在问题的描述中常用“缓慢”等语言叙述。分析研究对象的受力情况，根据已知力的变化情况确定未知力的大小或方向的变化情况。
三力平衡多用合成
三力平衡问题
建立平面直角坐标系，将不在坐标
轴上的力进行正交分解，列出Fx＝0 和Fy＝0进行求解
多共点力平衡问题
三、常见应用题型：
2.共点力的作用下动态平衡
动态平衡模型
是指通过控制某些物理量，使物体的状态发生缓慢的变化，而在此过程中物体始终处于一系列的平衡状态。
解题思路
解动态问题的关键是抓住不变量，依据不变的量来确定其他量的变化规律。化“动”为“静”，“静”中求“动”。

共点力平衡ppt课件

y
F1
F2
O
x
(2)正交分解各力：将每一个不在坐标轴上的力分解到 x 轴和
(2)将不在坐标轴上的力分解到坐标轴上；
y 轴上，并求出各分力的大小，如图所示．
y
(3)分别求出 x 轴、y 轴上各分力的矢量和，即：
Fx＝F1x＋F2xF2
＋… F1y F2y
F1
Fy＝F1y＋F2y＋…
F1x x
F2X O
的物体
动
面上
FN
Ff
mg
匀速下落的雨物体沿斜面匀
滴
速下滑
FN
Ff
mg
水平匀速行驶
的汽车
1、将物体所受重力按力的作用效果进行分解，下列图中错误的
是（ C ）
A．
B．
C．
D．
PA R T. 3
求共点力的合力
力的正交分解法
1）原理：把一个已知力沿着两个互相垂直的方向进行分解。
2）步骤：
(1)建立xoy直角坐标系
之间的动摩擦因数取 0.4，为使儿童在滑梯游戏时能在
滑板上滑下，滑梯至少要多高？
【分析】将滑梯抽象为一个斜面的模型，以正在匀速滑下
的小孩为研究对象。
小孩受到三个力的作用：重力G、斜面的支持力FN和滑动
摩擦力 Ff 。
当这三个力的合力为0时，小孩
能在滑板上获得一定速度后匀
速滑下，则斜面的高度即为所
2
2
(4)求共点力的合力：合力大小 F＝ Fx＋Fy，合力的方向与
Fy
x 轴的夹角为 α，则 t轴上个分力矢量和，即
Fx = Fx1 +Fx2+ Fx3+……
Fy = Fy1+Fy2+ Fy3+……

新版人教版必修1共点力平衡专题 (共27张PPT)学习PPT

警示1：:注意“死节”和“活节”问题
C.μ(mgcosθ－Fsinθ) （2）正确判断力的变化方向及方向变化的范围。
三段不可伸长的细绳OA、OB、OC能承受的最大拉力相同，它们共同悬挂一重物，如图示。
D. Fcosθ－mgsinθ 如图所示，质量为m的物体用细绳OC悬挂在支架上的O点，轻杆OB可绕B点转动，求细绳OA中张θ 力T大小和轻杆OB受力N大小。
15
4.相似三角形法：分析动态平衡问题：
正确作出力的三角形后，如能判定力的三角形与图形中已知长度的三角形（几何三角形）相似，则可用相似三角形对应边成比例求出三角形中力的比例关系，从而达到求未知量的目的。
题型特点：（1）三个力，（2）其中一个力为恒力，（3）另两个力的大小和方向均发生变化，则此时用相似三角形分析。
θ
N不变，T变小 D.
隔离物体，受力分析，画出受力图
斜面夹角θ，物体重力mg, 求斜面对物 μ(mgcosθ－Fsinθ)
B．绳OA的拉力逐渐减小；
例2：半圆形支架BAD上悬着两细绳OA和OB，结于圆心O，下悬重为G的物体，使OA绳固定不动，将OB绳的B端沿半圆支架从水平位
体的支持力和摩大小如何变化？
共点力的平衡问题专题
1
一.共点力: 作用在物体的同一点，或作用线延长相交于一点的几个力称为共点力。
N
f 刹车 G
F1 限速
40km/s G
F2
F1
F3
F2
不是共点力
❖作力的示意图时，可以把这些力的作用点画到它们作用线的公共交点（重心）上。
2
二、平衡状态 (加速度a=0)
物体处于静止或者匀速直线运动的状态叫做平衡状态。
• A．FN１和FN2 • B．FN１和FN2都减小 • C．FN１增大，FN2 • D．FN１减小，FN2增大

《共点力的平衡》课件

Ppt
《共点力的平衡》PPT课件
单击添加副标题
Hale Waihona Puke 汇报人：PPT目录01 03 05 07
单击添加目录项标题
02
共点力平衡的概念
04
共点力平衡的实例分析
06
共点力平衡的实验验证
08
课件介绍共点力平衡的分类共点力平衡的应用
总结与回顾
01
添加章节标题
02
课件介绍
课件背景
课件目标：介绍共点力的平衡概念、原理
结构稳定性设计原则：介绍结构稳定性设计的基本原则和注意事项
运动物体在运动过程中的平衡问题
运动物体在运动过程中的平衡条件
共点力平衡的应用实例
运动物体在运动过程中的平衡问题解决方法
共点力平衡的应用范围和局限性
07
共点力平衡的实验验证
实验目的和原理
添加标题
实验目的：通过实验验证共点力的平衡条件
总结与回顾：对课件内容进行总结，并回
顾重点知识点
作业与思考题：布置相关作业和思考题，供学生练习和思考
03
共点力平衡的概念
共点力的定义
共点力：作用在物体上同一点的力
平衡状态：物体处于静止或匀速直线运动状态
共点力平衡：物体受到的共点力合力为零，处于平衡状态
平衡条件：合力矩为零
和应用
课件内容：包括共点力的定义、平衡条件、
应用实例等
课件特点：采用图文结合的方式，生动形象地展示共点力的平衡原理
和应用
适用对象：适用于高中物理教学和学习者
课件目的
掌握共点力的平衡条件
理解物体平衡状态及其条件
学会运用共点力的平衡条件解决实际问题

共点力的平衡ppt课件

的弹力。
FN1 FN2
FN1
G
cos
G F =FN1
FN 2 G tan
解题方法：（2）三角形法
三角形定则：三个力构成首尾相连的矢量三角形。
FN1
FN1
FN2
G FN2
FN1
G
cos
FN 2 G tan
解题方法：（3）正交分解法
y
FN1 FN1x
FN1y FN2
G
FN1X FN1 sin FN 2
x
FN1Y FN1 cos G
FN1
G
cos
FN 2 G tan
F合
三种方法求解：
T FN
G
例3.如图所示，电灯静止，其重力G=10N，已知绳 OA与竖直墙壁夹角为300，绳OB水平。则绳OA及绳OB所受到的拉力大小各是多少？
F =Fc=G FA a
A
a
B
O
FB
O
C
Fc=G
动态平衡问题：
第五节共点力的平衡
一、知识点
1．如果一个物体在力的作用下保持静止或匀速直线运动状态，则这个物体就处于平衡状态。
2. 二力平衡即二力合力为零。 3．在共点力作用下物体的平衡条件是
F合＝0。
4．对平衡状态的理解静止状态: v＝0且a＝0。匀速直线运动状态：v＝定值，且a＝0。
平衡状态：a＝0，即F合＝0
｛或 Fx合＝0
Fy合＝0
二、共点力平衡的几种常见类型
1．二力平衡：等大反向，是一对平衡力。用平衡力知识求解。
F合＝0
2．三力平衡： F合＝0
解题方法：（1）力的合成法：据平衡条件，任两个力的合力与第三个力等大反向

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

13
• 例3：如图所示，固定在水平面上的光滑半球，球心O的正上方固定一个小定滑轮，细绳一端拴一小球，小球置于半球面上的A点，另一端绕过定滑轮，如图所示.今缓慢拉绳使小球从A点滑向半球顶
点（未到顶点），则此过程中，小球对半球的压力大小N及细绳的拉力T大小的变化情况是（）
•
A.N变大，T变大 B.N变小，T变大
共点力的平衡问题专题
1
一.共点力: 作用在物体的同一点，或作用线延长相交于一点的几个力称为共点力。
N
f 刹车 G
F1 限速
40km/s G
F2
F1
F3
F2
不是共点力
❖作力的示意图时，可以把这些力的作用点画到它们作用线的公共交点（重心）上。
2
二、平衡状态 (加速度a=0)
物体处于静止或者匀速直线运动的状态叫做平衡状态。
结点A向上移动而保持O点的位置不变，则A点向上移动时
（
）
A．绳OA的拉力逐渐增大；
B．绳OA的拉力逐渐减小；
C．绳OA的拉力先增大后减小；
D．绳OA的拉力先减小后增大。
12
训4：如图所示，细绳一端与光滑小球连接，另一端系在竖直墙壁上的A点，当缩短细绳小球缓慢上移的过程中，细绳对小球的拉力、墙壁对小球的弹力如何变化？
▪ ①OA、OB、OC三根绳子拉力的大小。
▪ ②A点向上移动少许，重新平衡后，绳中张力如何变化？
▪
B
▪
OA
C
上一页下一18页
▪ 警示2：注意“死杆”和“活杆”问题。 ▪ 如图所示，质量为m的物体用细绳OC悬挂
在支架上的O点，轻杆OB可绕B点转动，求细绳OA中张力T大小和轻杆OB受力N大小。
• 解题思路：（1）明确研究对象。（2）分析物体的受力。（3）用力的合成或力的分解作平行四边形（也可简化为矢量三角形）。（4）正确找出力的变化方向。（5）根据有向线段的长度变化判断各个力的变化情况。
• 注意几点：（1）哪个是恒力，哪个是方向不变的力，哪个是方向变化的力。 • （2）正确判断力的变化方向及方向变化的范围。 • （3）力的方向在变化的过程中，力的大小是否存在极值问题。
9
3、图解法：分析动态平衡问题
•动态平衡问题：通过控制某一物理量，使物体的状态发生缓慢变化的平衡问题，从宏观上看，物体是运动变化的，但从微观上理解是平衡的。
• 所谓图解法就是通过平行四边形的邻边和对角线长短的关系或变化情况，做一些较为复杂的定性分析，从图形上一下就可以看出结果，得出结论。
• 题型特点：（1）物体受三个力。（2）三个力中一个力是恒力，一个力的方向不变，由于第三个力的方向变化，而使该力和方向不变的力的大小发生变化，但二者合力不变。
上一页下一8页
• 例2：半圆形支架BAD上悬着两细绳OA和OB，结于圆心O，下悬重为G的物体，使OA绳固定不动，将OB绳的B端沿半圆支架从水平位置缓慢移至竖直的位置C的过程中，如图所示，分析OA绳和OB绳所受力的大小如何变化？
TA是一直变小，而TB却是先变小后增大，当OB与OA垂直时TB最小。
5
｛ 2、力的分解法正交分解法效果分解法
将物体所受的共点力正交分解，根据平衡条件： F合=0 得：
X轴上合力为零： Fx=0 y轴上合力为零： Fy=0
6
▪ 训练
θ
斜面夹角θ，物体重力mg, 求斜面对物体的支持力和摩擦力大小
上一页下一7页
▪ 新学案p66 T3 ▪ p65 T6 ▪ p68 T4
•
C.N不变，T变小 D.N变大，T变小
14
【解析】对A进行受力分析，如图所示，力三角形AF′N与几何三角形OBA相似，由相似三角形对应边成比例，解得N不变，T变小.
15
4.相似三角形法：分析动态平衡问题：
正确作出力的三角形后，如能判定力的三角形与图形中已知长度的三角形（几何三角形）相似，则可用相似三角形对应边成比例求出三角形中力的比例关系，从而达到求未知量的目的。
题型特点：（1）三个力，（2）其中一个力为恒力，（3）另两个力的大小和方向均发生变化，则此时用相似三角形分析。
。解题的关键：是正确的受力分析，寻找力三角形和结构三角形相似
16
警示1：:注意“死节”和“活节”
问题
▪ 如图所示，长为5m的细绳的两端分别系于竖立在
地面上相距为4m的两杆的顶端A、B ，绳上挂一
三、平衡条件：
F合=0
F x
F y
0 0
1)二力平衡条件：（三同一反）大小相同；作用在同一直线；
作用在同一物体；方向相反。
2）三力平衡条件：任意两力的合力与第三个力大小相等方向相反作用在同一直线上。
3）多个力平衡的条件：
任意（n-1）个力的合力与第n个力大小相等方向相反，作用在同一直线上。3Fra bibliotek• 例1
个光滑的轻质挂钩，其下连着一个重为12N的物
体，平衡时，问： ①绳中的张力T为多少?
B
A
αα
②A点向上移动少许，图
重新平衡后，绳与水平面夹角，绳中张力如3何3 变化?
上一页下一17页
▪ 如图所示，AO、BO和CO三根绳子能承受的最大拉力相等，O为结点，OB与竖直方向夹角为θ，悬挂物质量为m。求：
四、共点力的平衡解题方法
已知物体重力мg, 绳与墙夹角θ，求墙对球的支持力和绳对球的拉力大小
θ
4
四、共点力的平衡解题方法 1、力的合成法
将物体所受的某几个力合成，将问题转化为二力平衡。
步骤 1）.正确选取研究对象 2）.隔离物体，受力分析，画出受力图 3）.根据共点力平衡特点，利用几何关系求解
10
• 训2：如图所示，把球夹在竖直墙AC和木板BC之间，不计摩擦，球对墙的压力为FN１，球对板的压力为FN2．在将板BC逐渐放至水平的过程中，下列说法中，正确的是（）
• A．FN１和FN2 • B．FN１和FN2都减小 • C．FN１增大，FN2 • D．FN１减小，FN2增大
11
训3：如图所示，电灯悬挂于两壁之间，更换水平绳OA使连
A
θO B
C 图 37
mg
上一页下一19页
▪ 如图所示，水平横梁一端A插在墙壁内，另一端装有小滑轮B，一轻绳一端C固定于墙壁上，另一端跨过滑轮后悬挂一质量为 m=10kg的重物，，则滑轮受到绳子作用力为：
▪ A. 50N B. C. 100N D.
C
30o
B
A
图 38
m
上一页下一20页
上一页下一21页