光栅衍射及光栅光谱
- 格式:ppt
- 大小:541.50 KB
- 文档页数:4


光栅衍射【实验简介】光栅是一种折射率周期性变化的光学元件。
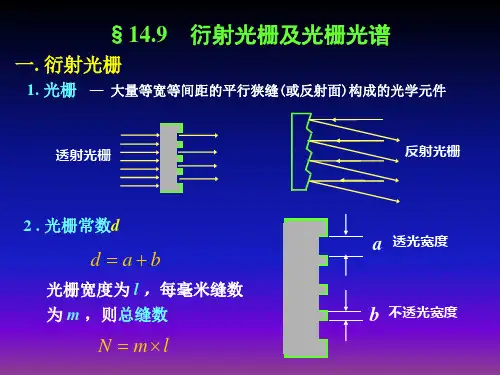
最常用的光栅是由大量等宽、等间距的平行狭缝组成的,通常是在一块平面玻璃上用金刚石刻制、复制或用全息照相等方法制成。
光栅是一种重要的分光元件。
光栅不仅适用于可见光波,还能用于红外和紫外光波,常被用来精确地测定光波长及进行光谱分析。
以衍射光栅为色散元件组成的摄谱仪和单色仪是物质光谱分析的基本仪器之一。
光栅衍射原理也是晶体X射线结构分析和近代频谱分析与光学信息处理的基础。
【实验目的】1.观察光栅的衍射光谱,理解光栅衍射基本规律;2.进一步熟悉分光计的调节和使用;3.学会利用光栅衍射测定光栅常数、光波长、角色散率。
【实验仪器】分光计,光栅,汞灯,平面镜等。
【实验原理】如图1所示,a为光栅刻痕宽度,光射到它上面向四处散射而透不过去,两刻痕之间宽度b =+为相邻两狭缝上相应两点之间的距离,称为光栅常数,它是光栅的相当于透光狭缝,d a b基本参数之一。
图1 光栅片示意图根据夫琅和费衍射理论,当波长为λ的平行光垂直投射到光栅上,通过每个狭缝的光都要产生衍射,若在光栅后面放置一会聚透镜,所有的衍射光通过透镜后将相互干涉,所以光栅的衍射条纹是单缝衍射和多缝干涉的总效果(见图2)。
对于衍射角为ϕ的衍射光波,相邻两缝对应点射出的光束的光程差为()sin sina b dϕϕ∆=+= (1) 当ϕ满足sin0,1,2,3d k kϕλ==±±± (2) 即光程差等于波长的整数倍时,该方向上的衍射光将相干相长,出现明纹。
式(2)称为光栅方程,其中k为明纹级数,0,1,2,3k=±±±所对应的条纹分别称为中央(零级)极大,正、负第一级极大,正、负第二级极大…等。
当衍射角ϕ不满足光栅方程时,衍射光或者相互抵消,或者强度很弱,几乎成为一片暗背景。
当平行光以入射角(光栅法线与入射光的夹角)射到光栅时,光栅方程应该写为(sin sin)0,1,2,3d i k kϕλ±==±±± (3)入射光与衍射光在光栅法线同侧时,上式中sin i前取正号;否则取负号。


光学中的光栅与光谱分析光栅是一种常见的光学元件,广泛应用于光学测量、光谱分析、光学通信等领域。
本文将从理论原理、光栅结构、光栅的工作原理以及光谱分析等方面对光栅进行介绍和分析。
一、光栅的理论原理光栅的理论基础可以追溯到著名的杨氏实验,即杨氏双缝干涉实验。
杨氏实验中,光经过两个狭缝后形成干涉条纹,其间距与入射光的波长、狭缝间距有关。
而如果将这两个狭缝换成许多等距离的狭缝,则可以得到一个光栅。
光栅的理论原理基于光的衍射现象。
当光通过光栅时,光栅会将入射光分成多个次级光波,并在特定方向上形成明暗相间的衍射图案。
这些次级光波的干涉效应造成了光栅上出现的多重条纹,称为光栅的衍射光谱。
二、光栅的结构光栅主要由一系列平行的透明或不透明条纹组成,这些条纹可以是等宽的,也可以是非等宽的。
光栅的条纹间距是光栅常数,通常用d表示。
光栅常数决定了光栅的分辨率和光谱的光谱范围。
光栅的常见结构包括平行光栅、棱柱光栅以及体积光栅。
平行光栅是最常见的光栅类型,由等宽平行条纹组成。
棱柱光栅的条纹是由棱面组成的,可以用于更复杂的光学系统中。
体积光栅是一种将条纹刻在介质内部的光栅,具有更高的分辨率和光谱纯度。
三、光栅的工作原理光栅通过衍射现象实现光的分光,可以将入射光按照波长分解成不同的光束。
当入射光通过光栅时,每个波长的光经过衍射后会形成不同的衍射角。
这些衍射角和光的波长之间有着特定的关系,通过测量衍射角可以使用光栅来进行光谱分析。
光栅的工作原理可以用衍射公式来描述。
对于光栅上的第n级次发生衍射,光栅衍射公式为:sinθ = nλ / d其中,θ为衍射角,n为衍射级次,λ为入射光的波长,d为光栅常数。
通过测量衍射角θ,可以计算出入射光的波长,从而实现光谱分析。
四、光谱分析光谱分析是光栅应用的重要领域之一。
光栅可以用于实现高分辨率的光谱测量和光谱分析。
通过测量光栅上的衍射光谱,并分析其中的条纹或峰值,可以获取样品的成分、浓度以及其他光学性质。



122 实验5-12 光栅衍射【实验目的】1.观察光栅的衍射光谱,理解光栅衍射基本规律。
2.测量光栅常数、光波波长和光栅角色散率。
3.进一步熟悉分光计的调节与使用。
【实验器材】分光计、平面透射光栅、汞灯。
【实验原理】一、衍射光栅和光栅方程光栅和棱镜一样,是一重要的分光光学元件,已广泛应用在摄谱仪、单色仪等光学仪器中。
广义地说,具有空间周期性排列的物体都叫光栅,如金属中的晶格点阵就是很好的立体光栅。
在实验室中所用的光栅是由一组数目极多、平行排列的、等宽等间距的狭缝构成。
利用透射光工作的称为透射光栅,利用反射光工作的称为反射光栅。
本实验用的是平面透射光栅。
原制平面透射光栅是由金刚石刻刀或激光刻纹机在精致的平行平面的光学玻璃上刻划而成的。
刻纹刀经过的地方变毛,光射到它上面向四处散射而透不过去,两刻痕之间相当于透光狭缝。
原制光栅是很昂贵的,实验室中所用的一般都是复制光栅。
设透光宽度为a ,不透光(刻痕处)宽度为b ,则b a d +=即为两狭缝间的距离,称为光栅常数,它是光栅基本参数之一。
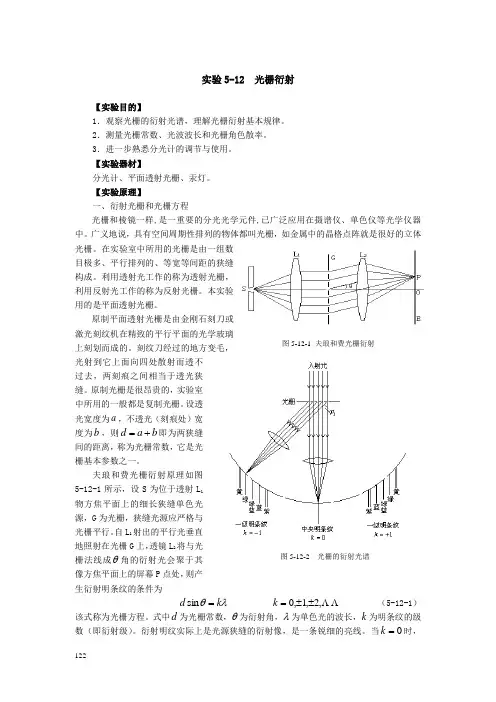
夫琅和费光栅衍射原理如图5-12-1所示,设S 为位于透射L 1物方焦平面上的细长狭缝单色光源,G 为光栅,狭缝光源应严格与光栅平行。
自L 1射出的平行光垂直地照射在光栅G 上,透镜L 2将与光栅法线成θ角的衍射光会聚于其像方焦平面上的屏幕P 点处,则产生衍射明条纹的条件为 λθk d =sin,2,1,0±±=k (5-12-1)该式称为光栅方程。
式中d 为光栅常数,θ为衍射角,λ为单色光的波长,k 为明条纹的级数(即衍射级)。
衍射明纹实际上是光源狭缝的衍射像,是一条锐细的亮线。
当0=k 时,图5-12-1 夫琅和费光栅衍射图5-12-2 光栅的衍射光谱123在0=θ的方向上,形成中央明纹,即零级明纹。
其它级次的条纹将对称地分布在中央明纹的两侧。
由于单缝衍射的制约,中央明纹最亮,其它依次减弱。
如果入射的是白光,则当0=k 时,在0=θ的方向上,各种波长的明纹重叠在一起,即中央明纹为白色,而其它同级次(k 相同)的衍射光将依次按波长的不同而分开,形成彩色的衍射光谱, 如图5-12-2。
光栅衍射实验⼗光栅衍射光栅(⼜称为衍射光栅)是⼀种分光⽤的光学元件。
过去制作光栅都是在精密的刻线机上⽤⾦刚⽯在玻璃表⾯刻出许多平⾏等距刻痕作成原刻光栅,实验室中通常使⽤的光栅是由原刻光栅复制⽽成的。
后来随着激光技术的发展⼜制作出全息光栅。
光栅的应⽤范围很⼴,不仅⽤于光谱学(如光栅光谱仪),还⼴泛⽤于计量(如直线光栅尺)、光通信(光栅传感器)、信息处理(VCD、DVD)等⽅⾯。
⼀、实验⽬的1.理解光栅衍射的原理,研究衍射光栅的特性;2.掌握⽤衍射光栅精确测量波长的原理和⽅法;3.进⼀步熟悉分光计的⼯作原理和分光计的调节、使⽤⽅法。
⼆、实验原理衍射光栅简称光栅,是利⽤多缝衍射原理使光发⽣⾊散的⼀种光学元件。
它实际上是⼀组数⽬极多、平⾏等距、紧密排列的等宽狭缝,通常分为透射光栅和平⾯反射光栅。
透射光栅是⽤⾦刚⽯刻⼑在平⾯玻璃上刻许多平⾏线制成的,被刻划的线是光栅中不透光的间隙。
⽽平⾯反射光栅则是在磨光的硬质合⾦上刻许多平⾏线。
实验室中通常使⽤的光栅是由上述原刻光栅复制⽽成的,⼀般每毫⽶约250-600条线。
20世纪60年代以来,随着激光技术的发展⼜制造出了全息光栅。
由于光栅衍射条纹狭窄细锐,分辨本领⽐棱镜⾼,所以常⽤光栅作摄谱仪、单⾊仪等光学仪器的分光元件,⽤来测定谱线波长、研究光谱的结构和强度等。
另外,光栅还应⽤于光学计量、光通信及信息处理。
图10-1光栅⽚⽰意图设平⾯单⾊光波垂直⼊射到光栅(图1)表⾯上,衍射光通过透镜聚焦在焦平⾯上,于是在观察屏上就出现衍射图样,如图2所⽰。
光栅⽅程: sin d k φλ= (0,1,2,...k =±±)图10-2 单⾊光光栅衍射光谱⽰意图图10-3 复合光光栅衍射光谱⽰意图当⼊射光为复合光时,在相同的d 和相同级别k 时,衍射⾓φ随波长增⼤⽽增⼤,这样复合光就可以分解成各种单⾊光。
(如图3所⽰)根据光栅⽅程,若已知光栅常数,条纹级别能数出来,我们可以根据衍射⾓测量某光的波长。
§17.11 光栅衍射一.光栅(grating)• 光栅是现代科技中常用的重要光学元件。
• 光通过光栅衍射可以产生明亮尖锐的亮纹,复色光入射可产生光谱,用以进行光谱分析。
1. 光栅的概念光栅是由大量的等宽等间距的平行狭缝(或反射面)构成的光学元件。
从广义上理解,任何具有空间周期性的衍射屏都可叫作光栅。
2. 光栅的种类:光栅最早由Rittenhouse发明,此后夫琅禾费又在1819年独立制成。
透射光栅反射光栅(闪耀光栅)3. 光栅常数光栅常数是光栅空间周期性的表示.设:a 是透光(或反光)部分的宽度,b 是不透光(或不反光)部分的宽度,则:d = a+b ----光栅常数普通光栅刻线为数十条/mm ─ 数千条/mm,用电子束刻制可达数万条/mm(d ~10-1μm)。
二. 光栅的夫琅禾费衍射1.光栅各缝衍射光的叠加衍射角相同的光线,会聚在接收屏的相同位置上。
衍射:每个缝衍射在衍射角相同的地方有相同的条纹干涉:缝与缝之间将产生干涉,这是一种多缝干涉•以双缝的夫琅和费衍射光的叠加为例来分析:干涉条纹各级主极大的强度将不再相等,而是受到了衍射的调制。
但是各个干涉主极大的位置仍由 d 决定,而没有变化。
2. 多光束干涉(multiple-beam interference)先不考虑衍射对光强的影响▲ 明纹(主极大)条件:——正入射光栅方程(k = 0,1,2,…)光栅方程是光栅的基本方程设有 N 个缝,每个缝发的光在对应衍射角θ方向的 p 点的光振动的振幅为 E p,相邻缝发的光在 p 点的相位差为△φp 点为干涉主极大时,▲ 暗纹条件:各振幅矢量构成闭合多边形,多边形外角和:由(1),(2)得:由(3)和相邻主极大间有 N-1个暗纹和 N-2个次极大。
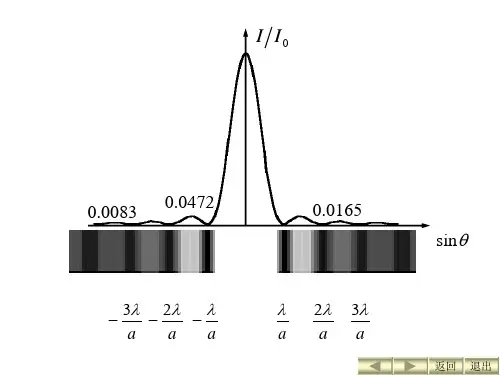
例如: N = 4,在 0 级和 1 级亮纹之间 k' 可取1、2、3,即有三个极小:N 大时光强向主极大集中,使条纹亮而窄3. 光栅衍射(grating diffraction)(1)各干涉主极大受到单缝衍射的调制。